Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.74 n.153 Medellín set./dez. 2007
CONTROL PREDICTIVO BASADO EN PREDICTORES BORROSOS
PREDICTIVE CONTROL BASED FUZZY PREDICTOR
MIGUEL ANGEL RODRIGUEZ BORROTO
Facultad de Ingeniería Eléctrica, Ph.D. Universidad Central de las Villas, Santa Clara, Cuba. marodrig@uclv.edu.cu
JOSE RAFAEL ABREU GARCIA
Facultad de Ingeniería Eléctrica, Ph.D. Universidad Central de las Villas, Santa Clara, Cuba. Abreu@uclv.edu.cu
SERGIO JIMENEZ GARCIA
Departamento de Ingeniería Electrónica, Msc. Instituto Tecnológico de Toluca, Estado de México. serjim@yahoo.com
BORIS LUIS MARTINEZ JIMENEZ
Facultad de Ingeniería Eléctrica, Msc. Universidad Central de las Villas, Santa Clara, Cuba. Boris@uclv.edu.cu
Recibido para revisar febrero 09 de 2007, aceptado abril 04 de 2007, versión final junio 06 de 2007
RESUMEN: En el presente artículo se expone un algoritmo para aplicar las técnicas de control predictivo lineal basadas en el modelo (MPC) al caso de procesos no lineales utilizando un predictor borroso (fuzzy), en base a la estructura Takagi_Sugeno_Kang_dinámica y bajo el principio de utilización de modelos lineales locales por tramos. Ello conduce inherentemente, a un proceso de adaptación de la matriz dinámica del sistema en cada periodo de muestreo, lo cual se considera novedoso en relación al MPC clásico. Se exponen los resultados de su aplicación al caso de un control de posición que utiliza un servo-motor de corriente continua con zona muerta y a un reactor continuo de tanque con agitador con reacción exotérmica. Los resultados son satisfactorios.
PALABRAS CLAVE: Control Predictivo, Control Borroso, Identificación borrosa, Predicción, Simulación de Sistemas, Control no Lineal.
ABSTRACT: In this paper an algorithm has been carried out with the aim to apply the technique of lineal model based predictive control (MPC) to non-linear process using a fuzzy predictor based on dynamical Takagi_Sugeno_Kang structure. The local step linearization principle is used. This principle inherently let us to develop an adaptation process of the system dynamical matrix in each sampled period. This approach is new in classical MPC. The algorithm was applied to some study cases such as a direct current servo system with dead zone and a continuous steered tank reactor with exothermic reaction and the main results has been presented. Such results are satisfactory in both cases.
KEYWORDS: Predicive Control, Fuzzy Control, Fuzzy Identification, Prediction, Simulation, Non-Linear Control.
1. INTRODUCCION
El control predictivo basado en el modelo (MPC) tuvo su origen en la década de los setenta con sus versiones originales conocidas como matriz dinámica (DMC) [1] y control basado en el modelo (MAC) [2]. Estos algoritmos computacionales para el control de procesos multivariables han ido ganando cada vez más desarrollo y popularidad en la industria y en el área académica [3].
Se presentan muchas variantes de métodos de MPC; existiendo variantes lineales y no lineales [4]. Se reporta gran cantidad de aplicaciones prácticas de estos algoritmos [5] y un gran porcentaje de las implementaciones son en sistemas multivariables.
La modelación borrosa, como método de identificación no lineal comenzó a emerger con fuerza en la década de los 90 [10].
Este impulso se debe a que se han desarrollado varias técnicas que permiten el entrenamiento de sistemas difusos a partir de datos medidos, junto a la ventaja de incorporar el conocimiento de expertos con relativa facilidad. En este trabajo se utiliza el sistema de inferencia fuzzy adaptativo combinado con redes neuronales (ANFIS) [12] para la identificación inteligente de la planta.
Como casos de estudio se toman: un servomotor de corriente directa con zona muerta y un reactor continuo de tanque con agitador; ambos procesos son no lineales inherentemente.
2. DESARROLLO
2.1 Control Predictivo Basado en el ModeloEl control predictivo basado en el modelo se fundamenta en la estructura mostrada en la Fig. 1 y consta de los siguientes pasos:
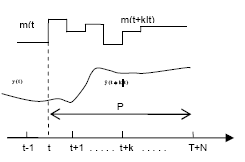
Figura 1. Estrategia MPC
Figure 1. MPC strategic
- Para una secuencia presente y futura de los movimientos de la señal de control Dm(k), Dm(k+1),...,Dm(k+M-1), el comportamiento futuro de la salida y(k+1|k), y(k+2|k), , y(k+P|k) puede ser predicho para un horizonte P, (horizonte de predicción).El pronostico en el instante t se efectúa usando un modelo del proceso para k = 1, 2, .,P; el valor predicho depende de los valores conocidos anteriores de la salida y de las futuras acciones de control en k = 0, 1, ..,P-1.
- El conjunto de M (M<P) movimientos futuros de la señal de control m se calcula mediante la optimización de un criterio que se establece para mantener la salida del proceso tan cerca como sea posible de una señal de referencia w(t+k) establecida a priori. Mas adelante en 2.4 se ofrecen mas detalles sobre el asunto.
- La señal de control m(t|t) se aplica al proceso mientras que las demás variaciones son rechazadas. En el próximo instante se calcula y(t+1) a partir de la secuencia anterior y de la presente. Se actualiza de nuevo el mando y se obtiene m(t+1|t+1). La implementación de esa estructura se indica esquemáticamente en la Fig.2. Intervienen en la misma los elementos esenciales: el modelo predictor y el optimizador.
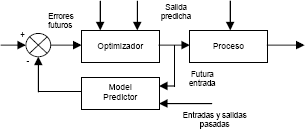
Figura 2. Esquema estructural de implementación del MPC
Figure 2. Structural squeme of MPC
Es fundamental en el MPC. Normalmente se consideran dos tipos de modelos: el del proceso real y el de los disturbios. En este caso se trata solamente el modelo del proceso. Prácticamente cualquier forma de modelo puede usarse en la formulación del MPC. Dos muy comúnmente usados son: respuesta al impulso y respuesta al paso.
2.2.1 Respuesta al Impulso
Se utiliza en MAC y en un caso especial de control predictivo generalizado. La salida truncada se relaciona con la entrada por la ecuación:
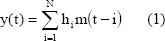
Donde; hi es la salida muestreada cuando el proceso es excitado por un impulso unitario. El número de muestras N, se elige de modo que se alcance la información exigida. El predictor basado en el modelo (1) se indica a seguidamente [13]:
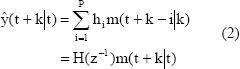
2.2.2 Modelo de Respuesta al Paso
Se usa en DMC, es muy similar al anterior; la señal de excitación es un paso unitario. La respuesta truncada es: 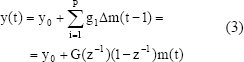
Donde; gi son las muestras de la respuesta de salida a un paso de entrada de amplitud:
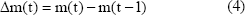
El predictor correspondiente es:
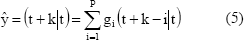
2.3 Predictor Basado en Lógica Borroso
La identificación borrosa es un método de identificación no lineal, particularmente interesante, que comenzó a emerger fuertemente en la década del noventa en el siglo pasado [14], [15]. Desde entonces se ha venido desarrollando y en el presente trabajo desempeña un papel esencial en la elaboración de un predictor para la salida de la planta, el cual se aplica en la implementación de un MPC para la misma.
2.3.1 Modelo Takagi-Sugeno-Kang (TSK)
El TSK puede ser tratado como una combinación de modelación lingüística y de regresión matemática en el sentido de que el antecedente describe regiones difusas del espacio de entrada donde el consecuente funcional es válido. Las reglas en este tipo de sistema son de la forma:
Ri: IF x1 is Ai1 and and xr is Air THEN yi=fi(x1,x2, ,xr)
Donde; los Aij son conjuntos borrosos y fi son funciones reales; para todos i, j enteros reales. Generalmente los fi son polinomios en las variables de entrada x1, ,xr.
Una parametrización útil en la práctica, que mejora la capacidad de aproximación de los modelos TSK, es la forma siguiente:
Ri: IF x1 is Ai1 and and xris Air THEN yi=bi0+bi1x1+ +birxr Con i = 1, ,L.
Donde L es el número de reglas, xi son las variables de entrada, yi son las variables de salida, Aij son conjuntos difusos caracterizados por las funciones de pertenencia mAij(xi) y bij son escalares.
Este modelo es conocido como TSK afín. Si la salida de un sistema difuso de este tipo aparece como una de sus entradas, obtenemos el llamado sistema difuso TSK dinámico. Este se construye a partir de las reglas:
Ri: IF x(k) is A1i and and x(k-n+1) is Ain and m(k) is Bi THEN yi = bi1x(k)+ +binxn(k-n+1) + bim(k)
Donde; m(k) es la entrada al sistema y x(k) = [x(k) x(k-n+1)] es el vector de estado del sistema.
2.3.2 Mecanismo de inferencia
La salida del sistema TSK es un promedio ponderado de los valores de los consecuentes de las reglas. La fórmula de inferencia es:
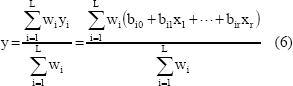
Donde; y es la salida del sistema, wi es el nivel de impacto de la regla i que se define como:
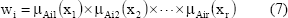
La ecuación (6) puede escribirse como:
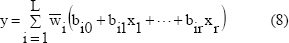
Donde 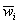 es el nivel de impacto normalizado y está dado por:
es el nivel de impacto normalizado y está dado por:
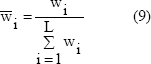
Para elaborar el modelo se utilizó la herramienta anfis de MATLAB. A partir del sistema de inferencia fuzzy desarrollado (SIF), se determina la función de transferencia del modelo de primer orden en cada punto de la trayectoria de estado.
2.4 Proceso de Optimización
Para cualquier conjunto presente y futuro de movimientos del mando Dm(k), Dm(k+1),..., Dm(k+m-1), el comportamiento de la salida del proceso 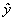 (t+1çk),
(t+1çk), 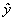 (t+2çk) ,...,
(t+2çk) ,..., 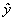 (t+NPçk) puede ser predicho sobre un horizonte P. Los M movimientos del control Dm (M < P) se calculan de modo que se minimice una función objetivo cuadrático del tipo:
(t+NPçk) puede ser predicho sobre un horizonte P. Los M movimientos del control Dm (M < P) se calculan de modo que se minimice una función objetivo cuadrático del tipo:
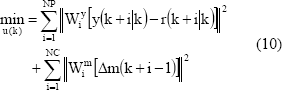
Donde; 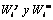 son las matrices pesantes. El vector de los futuros valores de la referencia, posiblemente variantes con el tiempo, se representa por r(k+i).
son las matrices pesantes. El vector de los futuros valores de la referencia, posiblemente variantes con el tiempo, se representa por r(k+i).
2.4.1 Diseño del MPC
Se demuestra [16] que el predictor de múltiples pasos en términos del modelo basado en la respuesta al impulso está dado por:
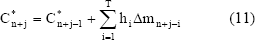
Donde; 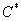 es el valor de la salida predicha y corregida. Matricialmente se puede escribir como:
es el valor de la salida predicha y corregida. Matricialmente se puede escribir como:

Los ai = gi i=1, . . .,NP solo valores de la respuesta al paso y se relacionan con los de la respuesta al impulso hj como:

Además;
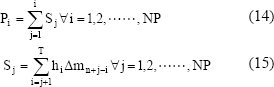
Tanto; Pi como Sj dependen de los hi y de los valores pasados de Dm. Esto permite definir los siguientes errores:
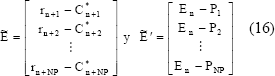
Donde; rn+i i=1, . . . ,NP representa la señal de referencia; 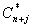 es la señal de salida predicha y corregida en el instante n+j;
es la señal de salida predicha y corregida en el instante n+j; 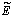 especifica los errores entre el set point y los valores de salida predichos corregidos. Mientras que
especifica los errores entre el set point y los valores de salida predichos corregidos. Mientras que 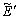 es una medida de los errores en lazo abierto. O sea, el error actual En se corrige por los Pi debidos a las acciones pasadas. No incluye las acciones futuras Dmn+j j ³ 0. Sin embargo,
es una medida de los errores en lazo abierto. O sea, el error actual En se corrige por los Pi debidos a las acciones pasadas. No incluye las acciones futuras Dmn+j j ³ 0. Sin embargo, 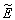 se refiere a la predicción en lazo cerrado pues se basa en acciones actuales y futuras de control..
se refiere a la predicción en lazo cerrado pues se basa en acciones actuales y futuras de control..
La matriz primer factor del segundo miembro de (12) es de orden NPxNC, se denomina matriz dinámica del sistema y se representa por:

En estos términos el funcional a optimizar según (10) se puede expresar como:
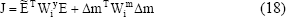
El cual resulta mínimo si:
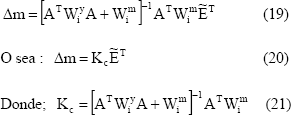
Es la ganancia del controlador predictivo lineal.
2.5 Algoritmo de Control
Se usa el MPC clásico (21) con adaptación de la matriz dinámica en cada instante de muestreo, gracias al TSK. El algoritmo se reduce a los siguientes pasos:
- En cada período de muestreo, a partir del sistema de de inferencia difuso (SIF), se calculan los parámetros de las funciones de membresía del conjunto borroso final y de ahí se determina los parámetros del modelo de regresión de la estructura TSK.
- Se determina un modelo lineal en la frecuencia, válido solamente en un entrono del punto de operación local, el cual permite determinar la respuesta al paso a partir de ese instante. De esa forma se actualiza la matriz dinámica local del proceso.
- Se calcula la ganancia del MPC lineal siguiendo el procedimiento descrito. Se calcula el vector de control y se aplica la planta su primer elemento.
- Se registra la salida y se repite el algoritmo a partir del paso (1).
3. RESULTADOS
A continuación se presentan los resultados alcanzados en los dos casos estudiados:
3.1 Control predictivo basado en un Modelo Fuzzy de un Servomoto
Se utilizó un servomotor del laboratorio de Automática del Departamento de Ingeniería Electrónica del Instituto Tecnológico de Toluca, marca Baldor, 110 V, 2.4 A, ¼ HP, 2200 rpm. La función de transferencia de este motor es:
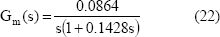
Y el mismo presenta un error umbral o zona muerta de ± 2 v. El modelo (21) predice la salida con un error del 2%. El modelo anterior, con la zona muerta, fue simulado durante 100 segundos, sometiéndolo a una señal de perturbación pseudo aleatoria de amplitud ± 10 voltios y frecuencia promedio de 5 rad/seg. Dicha señal y la respuesta del motor se muestran en la Fig. 3 y la Fig. 4 respectivamente. Se tomaron muestras de entrada y salida simultáneamente con un periodo de muestreo de 0.01 seg, formando los vectores de datos de entrada-salida.
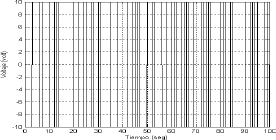
Figura 3. Señal seudo-aleatoria de entrada al motor.
Figure 3. Motor Pseudo-random input signal.
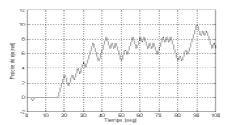
Figura 4. Posición del eje del motor al ser excitado por la señal de la Fig.3.
Figure 4. Out put position of motor rotor when it is exited by signal showed in Fig. 3.
3.1.1 Obtención del SIF para el servomotor
Para ello se toman las primeras 5000 muestras como datos entrenamiento de anfis. Las restantes 5001 muestras se toman como datos de chequeo del modelo borroso. A través de la herramienta de MATLAB después de varias pruebas y ensayos, se obtuvo el modelo, cuyo SIF posee las propiedades
que se indican a continuación:

El error promedio comparando con datos reales es de 0.08 aproximadamente.
Mediante este SIF, y aplicando el algoritmo descrito se diseña el MPC cuya respuesta a un paso de amplitud 5 rad en posición, se muestra en la Fig. 5. Los parámetros del MPC son: NP = 25, NC = 10, factor de peso en la salida 1 y factor de peso en el mando igual a 0.001. El comportamiento dinámico es aproximadamente críticamente amortiguado, con una exactitud alta.
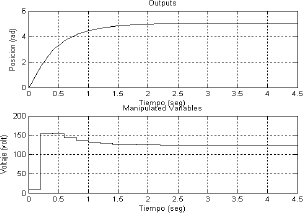
Figura 5. Comportamiento del MPC a un cambio tipo paso en la referencia de 5 radianes.
Figure 5. Performance of MPC exited by 5 radians step reference signal.
3.2 Control Predictivo Basado en un Modelo Fuzzy de un Reactor (RCTA)
El reactor se muestra en la Fig. 6. El modelo no lineal del mismo está dado por:
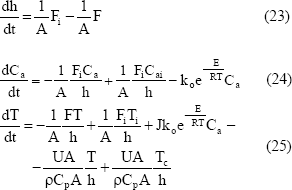
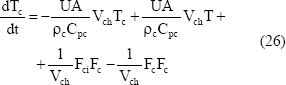
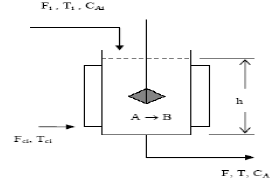
Figura 6. Esquema del RCTA
Figure 6. CSTR squeme.
Este modelo ha sido probado [17] y se toma como proceso real. Los flujos de entrada de reactivo Fi y flujo de refrigerante en la chaqueta de enfriamiento Fc son las señales de entrada al proceso, ya que el flujo total de salida se considera constante. La salida es la concentración de reactivo Ca. Similarmente al caso anterior, el modelo no lineal (23) a (26) se simula utilizando señales de ruido pseudo aleatorio en las válvulas de los flujos de entrada con propiedades estadísticas apropiadas. Para mas de talles acerca de la simulación se puede consultar [18].
Se tomaron muestras de las entradas y la salida cada 0.1 minuto durante tres horas. Se formaron los ficheros de datos de entrenamiento y de validación similarmente al caso anterior.
3.2.1 Obtención del SIF para el reactor
A partir de ANFIS y con esos datos, se determinó el modelo difuso del RCTA, resultando el SIF cuyos datos esenciales son:

Mediante este sistema, y aplicando el algoritmo descrito se diseñó el MPC cuya respuesta ante una entrada paso de 0,25 en el set point de Ca se muestra en la Fig. 7. Los parámetros de sintonía del MPC son: NP = 4, NC = 2, factor de peso en la salida 1 y factor de peso en el mando igual a 0.004.
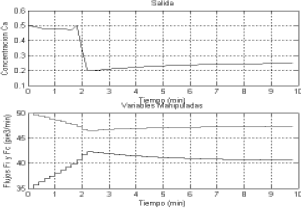
Figura 7. Comportamiento del MPC lineal usando un predictor fuzzy.
Figure 7. Lineal MPC performance using a fuzzy predictor.
Se aprecia un comportamiento dinámico satisfactorio a pesar del carácter no lineal del proceso. El desempeño del sistema es superior al que se logra con un predictor basado en el modelo determinístico no lineal (23) a (26) [19].
3. CONCLUSIONES
La gran exactitud que se logra con los modelos borrosos TSK dinámico permite establecer predictores no lineales muy efectivos para el diseño de MPC sobre la base del principio de linealización localizada sobre la trayectoria.
En ambos casos estudiados, la efectividad del algoritmo quedó evidenciada, observándose exactitudes similares a las del MPC lineal y a la del controlador clásico PID.
Como aspecto novedoso se destaca el carácter adaptativo de la matriz dinámica y la aplicación de modelos no lineales borrosos como predictor combinado con el MPC lineal.
REFERENCIAS
[1] CUTLER C.R. and RAMAKER B.C. Dymamic Matrix Control-A Computer Control of Industrial Processes. Automatic Control Conferency.San Francisco, USA. 1980. [ Links ]
[2] RICHALET J, RAULT A, TESTUD J.L. and PAPON J. Model Predictive Heuristic control: Application to Industrial Processes. Automática, 14(2):413-428, 1978. [ Links ]
[3] CAMACHO E.F. and BORDONS C, Model Predictive Control. Cap. 1 Springer-Verlag London Ltd. U.K, 1999. [ Links ]
[4] ALLOWER F. and ZHENG A. (Editors). Nonlinear Model predictive Control. Part I. Birkhauser Verlag, Basel-Boston-Berlin, 2000. [ Links ]
[5] BADWEL T.A. and QIN S.T. An overview of industrial predictive control technology. En D. P. Atherton and G. W. Irwin (Editores) Nonlinear Predictive Control Theory and practice. The inst. of electrical eng., London, U.K. , pag. 5, 2001. [ Links ]
[6] TOWNSEND S. and IRWIN G.W. Nonlinear model based predictive control using multiple local model. En D. P. Atherton and G. W. Irwin (Editors), Nonlinear Predictive Control Theory and Practice. The Institution of Electrical Engineers, London UK , pag. 223 – 242, 2001. [ Links ]
[7] SEBORG D.E, EDGAR T.F. and MELLICHAMP D.A. Process Dynamics and Control; JohnWiley & Sons, 1989. [ Links ]
[8] MORARI M, GARCIA C.E, LEE J.H. and PRETT D.M. Model Predictive Control; Prentice Hall, 1995. [ Links ]
[9] ESPINOSA J. and J. VANDEWALLE. Predictive Control Using Fuzzy Models, Submited to the 3rd. On-Line World Conference on Soft Computing in Engineering Design and Manufacturing, Springed-Verlag London Limited, pag. 187 – 201, 1999. [ Links ]
[10] SUGENO M. and KANG G.T. Successive identification of fuzzy model, Fuzzy Sets and systems, 28 (1), 15-30, 1988. [ Links ]
[11] YEN J, WANG L, and GILLESPIE W. A global local learning algorithm for identifying Takagi_Sugeno_Kang Fuzzy Model. 1998 IEEE International Conference on Fyzzy Systems. Anchorage, Alaska, May 4-9, 1998. [ Links ]
[12] JANG J. S.R, SUN C.T. and MIZUTANI E. Neuro-Fuzzy and soft computing. Prentice may, N.J., 1999. [ Links ]
[13] CAMACHO E.F, and BORDONSC. Model Predictive Control in the Proces Industry. Cap. 2, pag. 10. Springer-Verlag London Ltd. U.K, 1995. [ Links ]
[14] SUGENO M. and YASUKAWA T. A fuzzy-logic-based approach to cualitative modelling. IEEE Transaction on Fyzzy Systems, 1, 7-31, 1993. [ Links ]
[15] YAGER R.R and FILEV D.P. Unified structure and parameter identiufication of fuzzy model. IEE Trans. S. M. C.,23, 1198-1205, 1993.
[16] MARCHETTI J.L. MELLICHAMP D. A. and SEBORG D.E. Predictive Control Based on Discrete Convolution Models. Ind. Eng. Chem. Des. Dev., pag. 488-495, 1983. [ Links ]
[17] LUYBEN W.L. Modeling, Simulation and Control for Chemical Engineers. Cap. 3. McGraw Hill Book Co, 1973. [ Links ]
[18] RODRÍGUEZ BORROTO M. A. ABREU GARCÍA J. R, BACA GÓMEZ C. R. MARTÍNEZ JIMÉNEZ B. L. Modelado Borroso de un Reactor Continuo de tanque con Agitador con Reacción Exotérmica. (Publicarse por DYNA antes que el presente articulo). [ Links ]
[19] RODRÍGUEZ BORROTO M. A. Control Predictivo No Lineal de un Reactor con Restricciones. Memorias del XI Cong. Latinoamericano de Control Aut. Informática-2004. Habana, Cuba, Mayo, 2004. [ Links ]














