Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.75 n.154 Medellín jan./mar. 2008
MODELAMIENTO MATEMÁTICO DE FLUJO BIFÁSICO: EFECTO DE LA VELOCIDAD DE LA ONDA DE PRESIÓN SOBRE LA MAGNITUD Y DISTRIBUCIÓN DE PRESIONES
MATHEMATICAL MODELING OF TWO-PHASE FLOW: PRESSURE - WAVE VELOCITY EFFECT ON THE MAGNITUDE AND PRESSURES DISTRIBUTION
EDUARD ALBERTO GARCÍA
Ingeniero Agrícola M.Sc. Universidad de Puerto Rico – Mayagüez, Departamento de Ingeniería Civil, egg13345@uprm.edu
JAIRO ALEXANDER OSORIO
Profesor Asistente, Universidad Nacional de Colombia, Sede Medellín, Facultad de Ciencias Agropecuarias
MISAEL CORTES
Profesor Asistente, Universidad Nacional de Colombia, Sede Medellín, Facultad de Ciencias Agropecuarias
Recibido para revisión Marzo 01 de 2007, aceptado Mayo 14 de 2007, versión final Agosto 29 de 2007
RESUMEN: El accionamiento rápido de sistemas de control puede producir flujos transitorios en los cuales se alcanza la presión de vapor, produciéndose flujo en dos fases: líquido y vapor. En algunos casos, adicionalmente, puede ocurrir cavitación. En estas condiciones el flujo se caracteriza por variaciones espaciales y temporales de la velocidad de las ondas de presión debido a un incremento en la fracción de vacío. Típicamente la velocidad de la onda de presión en flujo bifásico se determina usando la suposición de proceso isotérmico, como en la ecuación de Wylie. En esta investigación, se introdujo el comportamiento de proceso politrópico y se obtuvo una nueva ecuación. Para verificar la validez de los resultados numéricos, se construyó un montaje experimental, los resultados obtenidos se usaron para analizar la respuesta del sistema y estudiar la variación de la velocidad de la onda a lo largo de la zona de cavitación vaporosa distribuida. Una buena predicción de la magnitud de la máxima presión con ambos modelos fue obtenida; sin embargo, comparado con los datos medidos, ambos modelos predicen mayores intervalos de tiempo entre pulsos de presión consecutivos. En general, mejores predicciones se obtuvieron con la expresión de velocidad de onda bajo flujo adiabático. El volumen de la cavidad de vapor fue similar para ambos métodos, ambos modelos predijeron la formación de cavidades adicionales no detectadas en los resultados experimentales.
PALABRAS CLAVE: flujo bifásico, cavitación vaporosa, velocidad de la onda de presión.
ABSTRACT: Quick movements of flow control system devices can produce transient flows where vapor pressure is reached, creating two-phase flows: liquid-vapor. Cavitation can be present in some cases. Under these conditions, the flow is characterized by spatial and temporal changes in the velocity of pressure waves due to an increase in the void fraction. Typically the wave velocity in two-phase flows is determined using an isothermal assumption like Wylies equation. In this research the adiabatic assumption was introduced and a new equation was obtained. Experimental set up was built; the results were used to analyze the system response and to study the wave velocity variation along the distributed vaporous cavitation zone and the vapor cavity. The experimental results were compared to numerical simulations assuming adiabatic and isothermal bubble vapor behavior. A good prediction of the maximum pressures magnitude was obtained with both models; however, both models predicted longer time intervals between consecutive pressure pulses compared to the measured data. In general, better predictions were obtained with the adiabatic wave velocity expression. The volume of the vapor cavity obtained by using adiabatic or isothermal behavior was similar; however, both models predicted the creation of additional cavities not detected in the experimental results.
KEYWORDS: two-phase flows, vaporous cavitation, pressure wave velocity.
1. INTRODUCCIÓN
La velocidad de la onda de presión durante condiciones de flujo en estado transitorio es función de las propiedades de la tubería, las propiedades del fluido y las restricciones de la tubería impuestas por las fronteras del sistema. Las propiedades de la tubería incluyen diámetro, espesor y material. Las propiedades del fluido incluyen el módulo de elasticidad volumétrico, la densidad del fluido, la viscosidad cinemática, y la cantidad de gases disueltos en el líquido. Las restricciones de la tubería se refieren al tipo de apoyo o anclaje y a la libertad de movimiento de la tubería (Chaudhry, 1987; Wylie et. al., 1993; Robertson. Et. al., 1998).
La cantidad de gases disueltos en el líquido decrece con la velocidad de la onda. Este efecto es significativo cuando la presión del líquido cae a valores por debajo de la presión atmosférica y se aproxima a la presión de vapor. Bajo estas condiciones la fracción de vacío aumenta debido a la formación de burbujas, formando una región de cavitación vaporosa (Padmanabhan, 1978; Simpson, 1986; Chaudhry, 1987). Por consiguiente, las velocidades de onda para pulsos de presión positivos son mayores que las velocidades de onda para pulsos de presión negativo. La formulación matemática para obtener la velocidad de la onda en un líquido puro es diferente a la de flujo bifásico o mezclas de gas-líquido en donde la fracción de vacío es una función del tiempo. Halliwell (1963), presentó una expresión para predecir la velocidad de la onda de presión en líquidos puros:
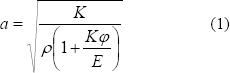
Donde a es la velocidad de la onda en un líquido puro (m/s), K es el módulo de elasticidad volumétrico (Pa), E es el módulo de elasticidad del material de la tubería (Pa), r es la densidad del líquido puro (kg/m3), y φ es un parámetro adimensional que depende de las propiedades elásticas de la tubería y de las condiciones de soporte. Halliwell (1963), derivó diferentes expresiones para el parámetro φ.
2. VELOCIDAD DE LA ONDA EN MEZCLAS GAS – LÍQUIDO
2.1 Comportamiento Isotérmico
La velocidad de la onda en una mezcla gas – líquido es menor que en un líquido puro. Tradicionalmente, la expresión para la velocidad de la onda bajo estas condiciones, se deriva realizando las siguientes suposiciones:
- La mezcla gas - líquido es homogénea, es decir, las burbujas de gas están uniformemente distribuidas en el líquido; por lo tanto es posible considerar una densidad promedio para la mezcla.
- Las burbujas de gas siguen un comportamiento isotérmico; por lo tanto la ecuación de gases ideales se puede expresar como pVg= p0V0, donde p es la presión para un tiempo t, Vg es el volumen de la fracción de gas en el tiempo t, p0 y V0 son la presión y volumen inicial de la fracción de vacío. Un comportamiento isotérmico, también implica que el módulo de elasticidad volumétrico del gas es igual a la presión, Kg = p.
- La presión al interior de las burbujas de vapor es independiente de la tensión superficial y de la presión de vapor del líquido.
Como podrá observarse en las siguientes expresiones, la velocidad de la onda en una mezcla gas – líquido depende de la presión y de la cantidad de gases contenidos en la mezcla. Bajo condiciones de flujo transitorio, ambos parámetros dependen del tiempo, por lo cual es necesario calcularlos para cada paso en el tiempo durante la solución de la ecuación diferencial gobernante.
Para la determinación de la velocidad de la onda en mezclas gas – líquido, las siguientes expresiones se encuentran disponibles en la literatura:
Tullis et al. (1976), durante flujo transitorio, aplicaron las ecuaciones de conservación de masa y momentum lineal a un fluido levemente compresible, obteniendo la siguiente expresión para la velocidad de la onda.
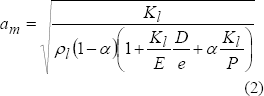
Donde am es la velocidad de la onda en una mezcla gas – líquido (m/s), 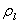 es la densidad del líquido puro (kg/m3),
es la densidad del líquido puro (kg/m3), 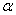 es la fracción de vacío, Kl es el módulo de elasticidad volumétrico del líquido (Pa), D es el diámetro de la tubería (m), E es el módulo de elasticidad del material de la tubería (Pa), P es la presión (Pa), y e es el espesor de la pared de la tubería (m). Note que esta ecuación desprecia la contribución de la fase gaseosa como parte de la densidad de la mezcla.
es la fracción de vacío, Kl es el módulo de elasticidad volumétrico del líquido (Pa), D es el diámetro de la tubería (m), E es el módulo de elasticidad del material de la tubería (Pa), P es la presión (Pa), y e es el espesor de la pared de la tubería (m). Note que esta ecuación desprecia la contribución de la fase gaseosa como parte de la densidad de la mezcla.
Chaudrhy (1987), presentó una expresión similar, pero consideró la contribución de la fase gaseosa a la densidad de la mezcla, dada por el término 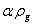 , donde
, donde 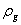 es la densidad del gas. La ecuación propuesta por Chaudrhy es
es la densidad del gas. La ecuación propuesta por Chaudrhy es
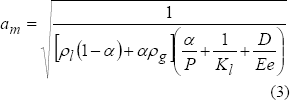
Las ecuaciones (2) y (3) están limitadas a tuberías elásticas de pared delgada con juntas de expansión frecuentes. Esta suposición se introduce por medio de la siguiente aproximación.
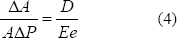
Donde 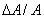 es el cambio de sección transversal de la tubería con respecto a su valor inicial. Este término representa la respuesta elástica de la tubería a los cambios de presión.
es el cambio de sección transversal de la tubería con respecto a su valor inicial. Este término representa la respuesta elástica de la tubería a los cambios de presión.
Padmanabhan (1978), derivó una expresión que incluye las restricciones de anclaje de la tubería y algunas propiedades de acuerdo al tipo de tubería, particularmente el material y el espesor, introduciendo un factor adimensional μ en la ecuación para velocidad de la onda, este factor es similar al factor j usado por Chaurdhry (1987). La expresión derivada por Padmanabhan está dada por:
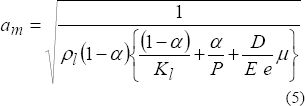
Wylie (1983), propuso otra expresión en la cual introdujo un coeficiente C1 adimensional, la ecuación es escrita como:
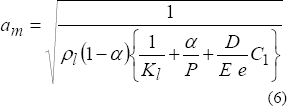
Las ecuaciones planteadas por Padmanabhan (1978) (5) y Wylie (1983) (6) son más generales que las otras aquí presentadas ya que en el análisis del término que involucra la respuesta elástica de la tubería ambos autores consideran un coeficiente adimensional (C1 ó m), que toma diferentes valores de acuerdo a las restricciones externas del sistema y al tipo de tubería. De las ecuaciones (5) y (6), es evidente que el coeficiente propuesto por Wylie es igual al propuesto por Padmanabhan (C1 = m) y que durante la derivación Wylie desprecia el efecto de la fase gaseosa sobre el módulo de elasticidad volumétrico del líquido.
Una notable diferencia entre ambas ecuaciones está dada por los términos 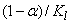 y
y 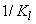 . La modificación proviene de la forma en que cada autor trata o aproxima el módulo de elasticidad volumétrico de la mezcla, Km. La expresión general para Km es:
. La modificación proviene de la forma en que cada autor trata o aproxima el módulo de elasticidad volumétrico de la mezcla, Km. La expresión general para Km es:
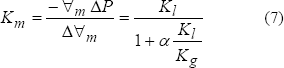
Donde Vm es el volumen inicial de la mezcla, DVm es el cambio de volumen correspondiente al cambio en presión DP.
Wylie (1983), asumió que Kl/Kg >> 1, lo cual convierte la ecuación (5) en la ec. (6). Bajo condiciones isotérmicas, la suposición realizada por Wylie es válida, debido a que el módulo de elasticidad volumétrico del líquido, Kl, es del orden de 109, mientras que para gases es igual a la presión, Kg=P, el cual puede ser del orden de 106, dando una razón de Kl/Kg @103. Una expresión alternativa para la ecuación de Wylie bajo condiciones isotérmicas es:
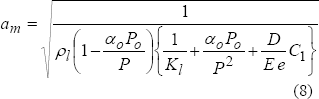
ao y Po son valores de referencia. La expresión anterior es útil para describir el comportamiento isotérmico de la fracción de vacío como una función de la presión durante el estado transitorio.
2.2 Comportamiento AdiabáticoLa suposición de un comportamiento adiabático para las burbujas de vapor, es uno de los principales aportes de esta investigación.
Para el caso de comportamiento adiabático, la fracción de vacío y el módulo de elasticidad volumétrico del gas, se expresan como:
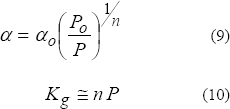
Donde n es el coeficiente politrópico para una expansión o compresión adiabática, el cual por definición, es igual a la razón de calores específicos 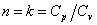 .
.
Usando las dos relaciones anteriores, y siguiendo un procedimiento similar al usado por Wylie (1983), la expresión obtenida para la velocidad de la onda de presión en mezcla gas líquido bajo comportamiento adiabático de las burbujas de vapor, está dada por:
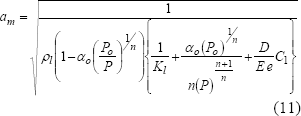
Un valor típico para n es 1.1, el cual se estima a partir de las tablas de presión de saturación del agua para un valor de la presión de vapor de 9700 Pa. Chaudrhy (1987), sugiere el uso de valores de n entre 1,2 y 1,4.
3. EQUIPO EXPERIMENTAL Y PROCEDIMIENTO
La fórmula propuesta por Wylie para comportamiento isotérmico y la propuesta en esta investigación para comportamiento adiabático, fueron comparadas con datos experimentales.
Para verificar la validez de los resultados numéricos obtenidos al aplicar la fórmula para la velocidad de la onda de presión con datos experimentales en la ecuación de movimiento, se construyó un montaje experimental y los resultados obtenidos se usaron para analizar la respuesta del sistema y estudiar la variación de la velocidad de la onda a lo largo de la zona de cavitación vaporosa distribuida.
El montaje experimental (Figura 1) consistió en una tubería (PVC-SCH-40) de 94 m de longitud y diámetro nominal de 2 pulgadas. El suministro de agua al sistema se realizó mediante un tanque de almacenamiento de carga constante, ubicado 8 m por encima del nivel de la tubería. A la entrada del sistema o condición de frontera aguas arriba, se ubicó una válvula reguladora de flujo (tipo globo), con la cual se generó el estado transitorio mediante un cierre rápido (0.107 s). Al final de la tubería o condición de frontera aguas abajo, se instaló un tanque de almacenamiento con carga constante (H=86 cm). La respuesta del sistema en el tiempo fue medida por medio de tres transductores de presión electrónicos Sensotec Pressure Transducer Model TJE, de rango 0 - 200 psia, con una precisión de 0.1% de la escala total del instrumento, ubicados al inicio, mitad y final de la tubería. Para la adquisición y almacenamiento de datos se utilizó un programa de adquisición de datos previamente desarrollado en LABVIEW; el programa permite ajustar la frecuencia o número de datos adquiridos por segundo, y el tiempo de muestreo a los valores deseados por el experimentador (10000 datos por segundo), así mismo el programa contó con un canal de adquisición por cada transductor, y adicionalmente permitía visualizar el fenómeno en proceso para tiempo real.
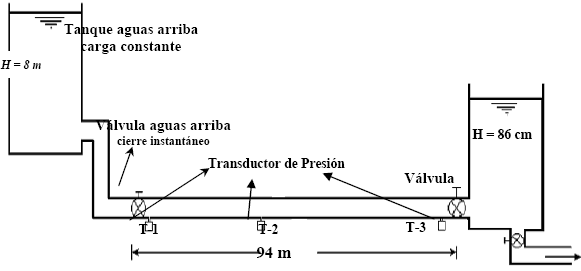
Figura 1. Esquema montaje experimental
Figure 1. Experimental setup
La Tabla 1 presenta los parámetros usados para el cálculo de la velocidad de la onda. La última fila representa el valor de la velocidad de la onda para un líquido puro usando la ecuación (1).
Tabla 1. Parámetros para el cálculo de la velocidad de la onda
Table 1. Parameters for calculation of pressure – wave velocity
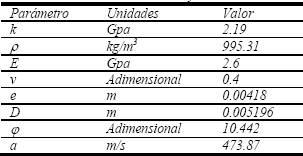
El factor de fricción en estado estable fue estimado usando la siguiente expresión:
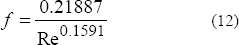
4. MODELO NUMÉRICO
En flujo de dos fases, mezcla vapor-líquido, los coeficientes de las ecuaciones gobernantes son altamente dependientes de la velocidad de la onda, la cual varía sensiblemente con el porcentaje de gases en la mezcla. Adicionalmente, el colapso de las cavidades de vapor por el paso de ondas de presión positivas, posibilita la formación de ondas de choque, limitando el uso de esquemas numéricos tradicionales como el método de las características, ya que es necesario incorporar las ecuaciones de la onda de choque como condiciones de frontera interna en la rejilla característica.
Para resolver las ecuaciones gobernantes de flujo transitorio en mezclas gas líquido, se usó el esquema de MacCormack citado por Anderson (1984) y Chaudrhry (1993). El uso del esquema de MacCormack en el tratamiento de las ecuaciones gobernantes para flujo bifásico o mezcla gas – líquido, fue introducido por Chaudrhry (1990). Sin embargo, durante el análisis Chaudrhry no consideró la generación y destrucción de burbujas de vapor debidas a la cavitación, y su estudio se redujo al rango de presiones positivas, es decir presiones muy por encima de la presión de vapor del líquido.
El segundo aporte realizado durante esta investigación consistió en la incorporación del uso del esquema numérico de MacCormack al tratamiento de las ecuaciones gobernantes para cavitación bajo flujo transitorio, el cual no ha sido presentado previamente en la literatura. El esquema de MacCormack es un esquema explícito, de dos pasos predictor – corrector, de segundo orden de exactitud ambos en el espacio y en el tiempo, y es capaz de capturar las ondas de choque generadas durante la cavitación sin necesidad de ajustes especiales para aislarla, Anderson (1984).
Las ecuaciones de conservación de masa (13) y conservación de momentum (14), incorporando la definición de densidad y velocidad de la onda de presión en la mezcla, son:
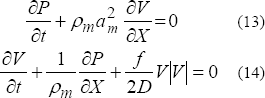
Aplicando a las ecuaciones anteriores la definición del esquema de Maccormack, definiendo el uso del símbolo ( * ) para referirse a la variable calculada durante el paso predictor, el símbolo ( ** ) para la variable calculada durante el paso corrector, la letra (j) para representar el nivel de tiempo conocido, y la letra (i) para el nodo espacial en estudio, la discretización de las ecuaciones (13) y (14) toma la forma.
Paso Predictor.
Ecuación de conservación de masa.
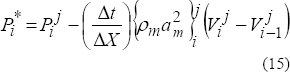
Ecuación de conservación de momentum.
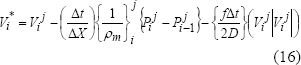
Paso Corrector.
Ecuación de conservación de masa.
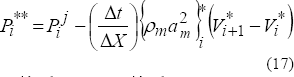
Ecuación de conservación de momentum.
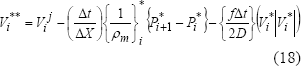
Las ecuaciones para velocidad de la onda en líquidos puros, y para condiciones adiabáticas e isotérmicas, fueron incorporadas al algoritmo numérico para comparación. La cavitación en el sistema fue generada a través del cierre súbito o rápido de la válvula en la frontera aguas arriba del sistema (0.107 s), creando un pulso de presión negativo que alcanzó los valores de la presión de vapor del líquido. El volumen de la cavidad de vapor generada en la frontera aguas arriba por separación de columna de flujo, fue obtenida por discretización de la ecuación de conservación de masa de acuerdo al procedimiento recomendado por Wylie (1993). Los valores de DX Dt se obtiene a partir de la condición de Courant para garantizar la convergencia del esquema numérico, Anderson (1984).
5. RESULTADOS
Los resultados experimentales indican la formación de una cavidad de vapor en la frontera donde se genera el flujo transitorio a través del cierre rápido de la válvula, donde para cada período de presión de vapor, se asocia la formación de una cavidad de vapor en la válvula.
La Figura 2, muestra los resultados numéricos obtenidos al asumir una velocidad de la onda para un líquido puro (ver ecuación 1), y sin considerar la formación de una cavidad en la válvula de cierre. Bajo estas condiciones, la onda de presión se desplaza con mayor rapidez en comparación a la experimental.
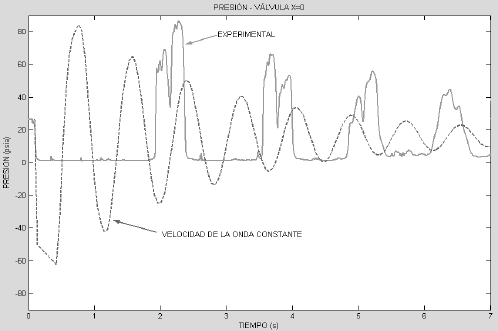
Figura 2. Comportamiento de la presión asumiendo velocidad de la onda constante Vs resultados experimentales
Figure 2. Pressure Behavior with constant pressure - wave velocity Vs experimental results
Adicionalmente, la historia de la presión obtenida con el modelo, muestra resultados sin significado físico de presión absoluta negativos. El modelo no reproduce los datos experimentales.
La Figura 3, muestra los resultados experimentales, y los resultados numéricos obtenidos considerando la formación de una cavidad de vapor en la válvula de cierre y velocidad de la onda usando la Ecuación 1. Se observa una buena predicción en tiempo de ocurrencia y magnitud de los dos primeros pulsos de presión, sin embargo los pulsos restantes presentan diferencias significativas en el tiempo de ocurrencia y magnitud; igualmente se observa mayor razón de disipación en comparación con los resultados experimentales.
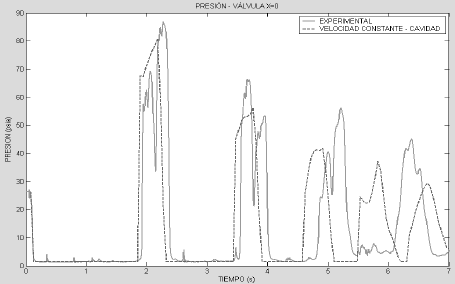
Figura 3. Comportamiento de la presión considerando formación de cavidad en la válvula Vs resultados experimentales
Figure 3. Pressure behavior considering a cavity formation at the valve Vs experimental results
La Figura 4, muestra la respuesta del sistema y los resultados calculados usando las ecuaciones para velocidad de la onda variable bajo condiciones isotérmicas y adiabáticas (Ecuaciones 8 y 11). Para el primer pulso de presión, con ambas ecuaciones, se obtiene una excelente predicción de la velocidad, tiempo de ocurrencia y magnitud de la onda; sin embargo, la velocidad de la onda bajo condiciones adiabáticas es mayor que la isotérmica en todo instante. Los pulsos de presión sucesivos se predijeron satisfactoriamente en magnitud, no obstante los resultados calculados no predicen exactamente el tiempo de ocurrencia. Para condiciones adiabáticas el segundo pulso de presión se presenta 0,14 s después del pulso experimental, y para condiciones isotérmicas el pulso ocurre 0,20 s después del experimental. Para el tercer pulso de presión, la predicción en el tiempo de ocurrencia es muy aproximada a la experimental. A partir de este pulso de presión ambos comportamientos se adelantan en el tiempo de ocurrencia del evento, sin embargo la predicción de la magnitud del pulso sigue siendo satisfactoria.
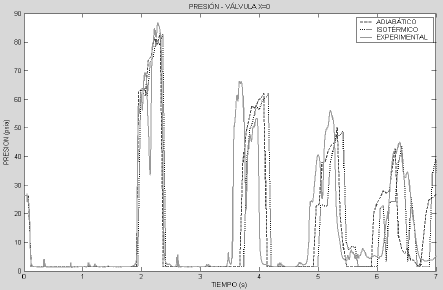
Figura 4. Comportamiento de la presión considerando cavitación vaporosa distribuida Vs resultados experimentales en X=0 (válvula de cierre)
Figure 4. Pressure behavior considering distributed vaporous cavitation Vs experimental results at X=0 (closing valve)
Cada pulso de presión positivo fue precedido por un período de presión de vapor, el cual forma una cavidad en la válvula. El tiempo de formación, duración y volumen de las cavidades de vapor, fue almacenado en el tiempo por medio del programa numérico desarrollado en Matlab®. La Figura 5, muestra el volumen de dichas cavidades de vapor como una función del tiempo, durante los períodos donde la presión de vapor fue alcanzada. Independiente del comportamiento asumido en la ecuación de velocidad de onda, comparado con los resultados experimentales, el modelo reproduce adecuadamente los tiempos de formación de los pulsos de presión positivos y negativos, por lo tanto, es posible afirmar que el modelo predice aceptablemente la formación y duración de las cavidades de vapor. Las correspondientes duraciones fueron 0.825 s en las mediciones experimentales, 0.802 s para comportamiento adiabático, y 0.817 isotérmico. Una cuarta cavidad puede ser observada en los resultados numéricos, la cual no fue apreciada en los resultados experimentales.
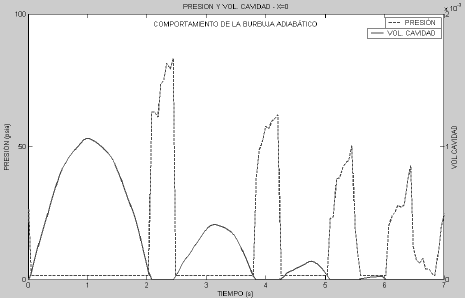
Figura 5. Cavidad de vapor en la válvula
Figure 5. Vapor cavity at the valve
La diferencia entre comportamiento adiabático e isotérmico se hace más clara al graficar la fracción de vacío para cada condición.
La Figura 6, compara las fracciones de vacío durante ambas condiciones al usar diferentes coeficientes politrópicos. El valor de n=1.4 corresponde a burbujas de aire. Se observa que para condiciones adiabáticas cualquier coeficiente politrópico usado, produce una fracción de vacío menor a la del comportamiento isotérmico. Esto explica la mayor velocidad de desplazamiento de la onda o desfase en el tiempo para condiciones adiabáticas observada en la Figura 4. Una menor fracción de vacío implica menores contenidos de vapor; consecuentemente, la mezcla tiende más a líquido puro, y por lo tanto la velocidad de la mezcla se aproxima más a la de líquido puro.
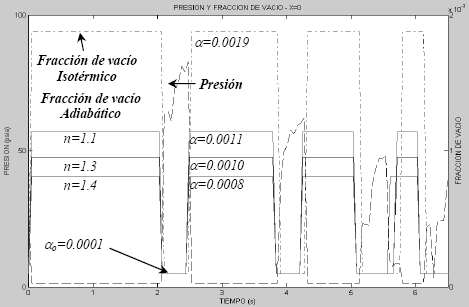
Figura 6. Comportamiento fracción de vacío y presión, en el tiempo
Figure 6. Void fraction and pressure behavior, in the time
Para el segundo punto en análisis (L/2), los resultados se muestran en la Figura 7. Se observó una respuesta en el tiempo similar a la obtenida para la primer sección (válvula - X=0). La predicción en la magnitud del pulso de presión positivo es aceptable para ambas condiciones o comportamiento de la burbuja, sin embargo, el modelo predijo presiones de vapor inexistentes para esta sección en condiciones experimentales.

Figura 7. Comportamiento de la presión contra resultados experimentales en X=L/2
Figure 7. Pressure behavior Vs experimental results at X=L/2
Adicionalmente, se observan oscilaciones de alta frecuencia atribuidas a la difusión numérica involucrada por el esquema numérico de segundo orden en el tratamiento del término convectivo de las ecuaciones gobernantes. Mayores oscilaciones se presentaron cuando un comportamiento de las burbujas de vapor isotérmico fue asumido.
La figura 8, muestra la velocidad de la onda en la mezcla como una función del tiempo. Se observa una fuerte dependencia entre la velocidad de la onda y la magnitud de la presión. Para condiciones de estado estable y una fracción de vacío inicial de ao = 0.0001, la velocidad inicial de la onda fue de 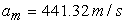 . Reducciones hasta del 75% fueron obtenidas bajo condiciones isotérmicas, y de hasta el 70 % bajo condiciones adiabáticas.
. Reducciones hasta del 75% fueron obtenidas bajo condiciones isotérmicas, y de hasta el 70 % bajo condiciones adiabáticas.
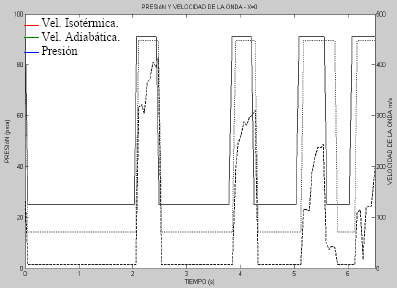
Figura 8. Velocidad de la onda de presión en el tiempo
Figure 8. Pressure – wave velocity in the time
6. CONCLUSIONES
Si se desea predecir adecuadamente el comportamiento de la presión en un flujo transitorio en dos fases o cavitación, es necesario el uso de expresiones para la velocidad de la onda que consideren la dependencia de ésta, con el gradiente de presión y la fracción de vacío. Los cálculos realizados en este trabajo muestran que si no se considera este efecto, los pulsos de presión no se predicen correctamente ni en tiempo de ocurrencia ni en magnitud.
La suposición de comportamiento isotérmico o adiabático de las burbujas de vapor, realizada durante la derivación de la ecuación para velocidad de la onda en flujo de mezcla gas – líquido, no representa diferencia significativa en la predicción de la magnitud del pulso de presión, sin embargo para la predicción en el tiempo de ocurrencia de los pulsos, se presenta desfase entre ellas, desplazándose con mayor rapidez bajo condiciones adiabáticas. Los resultados experimentales indican que el modelo que predice con mayor exactitud el tiempo de ocurrencia de los pulsos es el adiabático.
La magnitud o tamaño de la cavidad de vapor obtenido con ambos comportamientos es similar; a partir de la segunda cavidad se observa un desfase en el tiempo de formación de la burbuja.
En todos los casos estudiados se observó mayor razón de disipación del pulso de presión en la respuesta experimental que en la teórica. Lo anterior indica que están actuando otros factores de disipación de energía diferentes al factor de fricción para estado estable considerado en esta investigación. Algunos de esos factores de disipación de energía pueden ser la disipación de energía generada por el cambio de estado de las burbujas de agua a vapor, y la dependencia con la frecuencia de la velocidad del factor de fricción.
El esquema numérico de MacCormack ha sido introducido con eficacia en la solución de las ecuaciones gobernantes para el problema de flujo transitorio en dos fases o cavitación, los resultados obtenidos muestran concordancia con el fenómeno físico.
El esquema de MacCormack permite un desarrollo numérico más simple, en comparación con el conocido método de las características, en el cual es necesario desarrollar expresiones para predecir el comportamiento de la onda de choque generada en la interfase de las regiones de flujo bajo cavitación y golpe de ariete. Adicionalmente, para garantizar estabilidad, el método de las características requiere realizar interpolaciones en la rejilla de características.
REFERENCIAS
[1] ANDERSON D. A., TANNEHILL J. C. and PLETCHER R. H. Computational Fluid Mechanics and Heat Transfer. Hemisphere Publishing Corporation. New York USA . 1984. [ Links ]
[2] CHAUDHRY M.H. Applied Hydraulic Transients, Van Nostrand Reinhold Company, New York, USA , pp. 289 – 336. 1987. [ Links ]
[3] HALLIWELL A. R. Velocity of Waterhammer Wave in an Elastic Pipe, Jour. Hydr. Div., Amer. Soc, Civil Engrs. Vol. 89, No. HY4, pp. 1-21. 1963. [ Links ]
[4] PADMANABHAN M., AMES W. F. and MARTIN C. S. Numerical Analysis of Pressure Transients in Bubbly two – phase Mixtures by Explicit – Implicit Methods. Journal of Engineering Mathematics, Vol. 12 No. 1, January, pp. 83 - 93. 1978. [ Links ]
[5] ROBERSON J.A., CASSIDY J.J. and CHAUDHRY M.F. Hydraulic Engineering. John Wiley & Sons. New York, USA . 1997. [ Links ]
[6] SIMPSON A. R. Large Water Hammer Pressures Due to Column Separation In Sloping Pipes. Ph.D. Dissertation, University of Michigan. pp 275. 1986. [ Links ]
[7] TULLIS J. P., STREETER V. L. and WYLIE E. B. Waterhammer Analysis with Air Release. Proceeding 2nd International Conference on Pressure Surges, BHRA Fluid Engineering, London, England . Paper C3, pp. 35 – 47. 1976. [ Links ]
[8] WYLIE E.B. and STREETER V.L. Fluid Transients in Systems. Prentince Hall, New Jersey USA . pp. 463. 1993. [ Links ]














