Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.75 n.156 Medellín set./dez. 2008
UNA IMPLEMENTACIÓN HARDWARE OPTIMIZADA PARA EL OPERADOR EXPONENCIACIÓN MODULAR
A HARDWARE OPTIMIZED IMPLEMENTATION FOR THE MODULAR EXPONENTIATION OPERATOR
FREDDY BOLAÑOS
Profesor Auxiliar, Universidad Nacional de Colombia, Sede Medellín,fbolanosm@unal.edu.co
ÁLVARO BERNAL
Profesor Titular, Universidad del Valle, alvaro@univalle.edu.co
Recibido Noviembre 21 de 2007, aceptado Abril 04 de 2008, versión final Abril 10 de 2008
RESUMEN: Este documento muestra la optimización del operador Exponenciación Modular, aprovechando la gran flexibilidad de diseño que ofrecen el lenguaje VHDL y los dispositivos tipo FPGA. Debido a que el diseño se hace en un entorno limitado en hardware, la función de costo usada para la optimización considera tanto el tiempo de ejecución (desempeño) del operador, como el área ocupada por el mismo. La optimización se hace teniendo en cuenta tres alternativas distintas para la implementación del operador. Finalmente se comparan estas alternativas en términos de las funciones de costo asociadas a cada una y se discute la viabilidad de su implementación en entornos específicos.
PALABRAS CLAVE: Criptografía, Aritmética Modular, Lenguaje VHDL, FPGA.
ABSTRACT: This paper shows the optimization of the Modular Exponentiation operator, taking advantage of design tools such as the VHDL language and FPGA devices. Since the implementation occurs in a hardware–limited environment, the cost function used regarding optimization purposes includes both the execution time of the operator and the area occupied by the design. Three alternatives for the Modular Exponentiation operator have been considered. These alternatives are then compared in terms of their associated cost functions. Finally, the feasibility of the implementation of such alternatives in specific environments is discussed.
KEYWORDS: Cryptography, Modular Arithmetic, VHDL, FPGA.
1. INTRODUCCIÓN
La Exponenciación Modular es un operador de amplio uso en técnicas criptográficas tales como RSA [1], Rabin [2], Elgamal [3], McEliece [4] y otras. Básicamente el operador es el equivalente aritmético a calcular una exponenciación natural y luego calcular el modulo o residuo del resultado respecto a cierto número (M).
La Exponenciación Modular recibe tres operandos de entrada y se define de acuerdo con la ecuación (1).
En la ecuación, el operando X es llamado comúnmente la base de la exponenciación, el número Y es referido como el exponente y M es referido como el módulo de la representación.
Sean X, Y y M números enteros tal que: M>0. Se define la Exponenciación Modular P como:

Si y solo si existe un número entero k tal que:
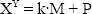
El requerimiento por niveles de seguridad cada vez más exigentes en los sistemas criptográficos modernos, obliga a un aumento paulatino en el tamaño en bits de las claves, de modo que los operadores que componen el sistema deben manejar operandos de mayor tamaño. Esta situación tiende a hacer lenta la ejecución de algunos de estos operadores, especialmente en aquellos de gran complejidad. Tal es el caso de la Exponenciación Modular, que debe operar sobre números enteros de gran tamaño representados normalmente en binario.
Existe entonces un interés por la optimización de tales operaciones, de modo que se puedan conseguir tiempos de ejecución aceptables. Las implementaciones en hardware aparecen como alternativa de diseño, ya que el hardware dedicado y optimizado para una operación es potencialmente más rápido que la ejecución de una aplicación software sobre hardware genérico.
El algoritmo binario es la primera aproximación práctica al problema del cálculo de la exponenciación modular [5]. Se trata de un algoritmo que tiene dos versiones, dependiendo del sentido en el que se recorre la representación binaria del exponente y está basado en la regla de Horner [6]. Esta regla básicamente expresa una manera alternativa y recursiva de representar un número binario en cierta base b, tal y como lo muestra la ecuación (2).
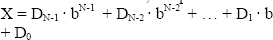
A partir de la representación alternativa propuesta en (2), es posible calcular el valor del número X usando menos productos que los necesarios para la forma de cálculo tradicional. El algoritmo binario aprovecha esta representación alternativa para el exponente (Y), de modo que en el cálculo de la Exponenciación Modular se requieran a lo sumo N productos modulares y N cuadrados. La ecuación (3) muestra cómo se logra esa representación alternativa del exponente para el algoritmo binario, donde b=2.
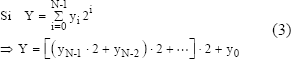
La figura 1 muestra el algoritmo binario en su versión derecha–izquierda, lo que significa que se recorre el exponente empezando por el menos significativo. Esta es la razón por la cual este algoritmo se conoce como LSB primero [7]. En la figura, N representa el tamaño en bits de los operandos involucrados en la Exponenciación.
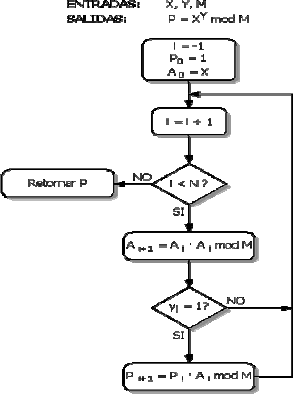
Figura 1. Algoritmo binario, versión derecha–izquierda
Figure 1. Left to right binary algorithm
La versión derecha–izquierda del algoritmo binario tiene una característica que la hace atractiva para una implementación en hardware. Obsérvese de la figura que se deben calcular un producto y un cuadrado por cada iteración. La ejecución del producto es condicional y dependerá de si el i–ésimo del exponente es uno o cero. Sin embargo, las dos operaciones son independientes entre si, de modo que podrían calcularse en paralelo. Una implementación hardware que aproveche está característica podría reducir el tiempo de ejecución a N productos equivalentes, en vez de los 2N que tardaría el algoritmo secuencial en el peor caso.
A partir de la forma básica del algoritmo binario se proponen una serie de optimizaciones, tendientes ya sea a reducir la cantidad de operaciones que es necesario calcular o la complejidad de tales operaciones, de modo que la Exponenciación Modular se pueda calcular en el menor tiempo posible. Tal es el caso del algoritmo m–ario [8], que parte de una representación diferente a la binaria (b>2) para reducir la cantidad de símbolos o dígitos que componen el exponente y consecuentemente, la cantidad de productos (iteraciones) que se deben calcular.
Este trabajo explora tres alternativas para el cálculo de la Exponenciación Modular y las compara en términos de una función de costo que considera tanto tiempos de ejecución como el área ocupada por la implementación. Este último parámetro es de gran importancia en entornos de desarrollo hardware sobre dispositivos FPGA. Todos los diseños hardware que se presentan han sido sintetizados usando dispositivos XC3S200 de Xilinx. Es común que en estos dispositivos la información de área ocupada se represente como la cantidad de celdas lógicas (CLB por sus siglas en inglés) necesarias para la implementación o como una fracción del total de celdas lógicas disponibles en el elemento que se requieren para la síntesis.
Retomando las ideas de [9], la función de costo queda definida como el producto entre el área ocupada y el tiempo de ejecución, tal y como lo muestra la ecuación (4).
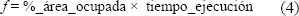
La metodología de optimización tendiente a minimizar el valor de f también es tratada en la referencia y propone la descomposición del operador Exponenciación Modular en una jerarquía organizada por niveles de complejidad. Se empieza con la optimización de los operadores de menor complejidad, para lo cual se implementan diversas alternativas y se les compara en términos de la función de costo escogida. Aquella implementación que exhiba un mejor comportamiento respecto a la función de costo, será la escogida para la implementación de operadores de mayor complejidad. El proceso se repite sucesivamente para cada nivel de la jerarquía hasta implementar el diseño completo.
2. ALTERNATIVAS PARA LA EXPONENCIACIÓN MODULAR
2.1 Exponenciación de Montgomery
El algoritmo de Montgomery se basa en una representación en la cual no es necesario hacer el ajuste de módulo (residuo) a los resultados de operaciones intermedias [10]. La representación es llamada imagen de Montgomery [11], y hace que los productos modulares del algoritmo de la figura 1 se conviertan en multiplicaciones de Montgomery, referidas en la figura 2 como el operador Mont. La figura 2 muestra la versión derecha–izquierda de la Exponenciación de Montgomery, que al igual que su contraparte binaria, permite una implementación paralela de los dos multiplicadores.
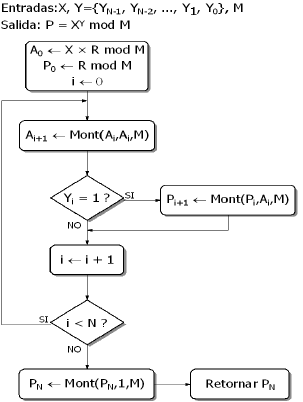
Figura 2. Algoritmo de Exponenciación de Montgomery, versión derecha–izquierda
Figure 2. Montgomerys Exponentiation Algorithm, left to right version
La tabla 1 muestra una comparación de desempeño entre los algoritmos binario y de Montgomery, partiendo del supuesto que la operación de cuadrado es equivalente en complejidad a un producto modular.
Tabla 1. Comparación de desempeño entre los algoritmos Binario y de Montgomery para la exponenciación modular
Table 1. Performance comparison between binary and Montgomery exponentiation algorithms
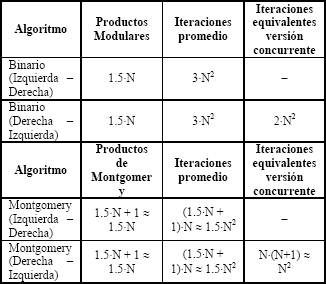
Dicha tabla muestra que en términos de la cantidad de productos que se deben calcular, el algoritmo de Exponenciación de Montgomery (en su versión concurrente) puede mejorar el desempeño del algoritmo binario (completamente secuencial) hasta en tres veces. Además debe considerarse que el producto o multiplicación de Montgomery es inherentemente más simple que el producto modular tradicional [12], lo que puede significar un aumento en la velocidad superior a 3.
La figura 3 muestra la ruta de datos (datapath) propuesta para el Exponenciador de Montgomery para operandos de N bits de longitud. Nótese la existencia de dos multiplicadores de Montgomery independientes, etiquetados como Πm en la figura. El registro de desplazamiento es el encargado de recorrer los bits del exponente y generar la señal Load_P, que representa la decisión que se debe tomar en cada iteración del algoritmo de la figura 2. El resto de elementos corresponde a multiplexores, registros y hardware de uso común.
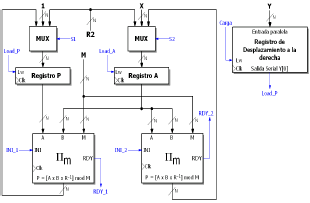
Figura 3. Estructura del Exponenciador de Montgomery
Figure 3. Montgomery exponentiation hardware structure
2.2 Recodificación del Exponente
El algoritmo binario de la figura 1 muestra cómo la cantidad de productos que se deben calcular es dependiente de la cantidad de ceros binarios que tiene el exponente. En el caso trivial en el que todos los bits del exponente son cero, se requiere de N productos modulares, mientras que si todos los bits del exponente son iguales a uno, se requerirá un total de 2×N productos modulares. La técnica por recodificación de exponente busca maximizar la cantidad de ceros que tiene la representación del exponente, con el propósito de hacer mínima la cantidad de operaciones necesaria. Se parte del supuesto que los productos se calcularán de manera secuencial, de lo contrario la estrategia no tiene mucho interés práctico.
Una representación binaria del exponente no aparece muy atractiva para la técnica propuesta. Debido a que la notación binaria es única, no hay oportunidad de maximizar la cantidad de ceros presente en la representación del exponente. La técnica de recodificación de exponente usa notación de dígito signado [13] para la representación del exponente, porque a partir de dicha representación, es posible maximizar la cantidad de dígitos iguales a cero. Esta notación es llamada también notación redundante, debido a que para cierto número entero, existen múltiples representaciones equivalentes.
Sea E un número entero cualquiera. Al conjunto de valores {dt, dt-1, , d1, d0}se le llama representación de dígitos con signo en base 2 de E, si y solo si:
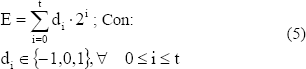
La figura 4 muestra el algoritmo para lograr la recodificación de un exponente en notación de dígito signado, de modo que la cantidad de ceros en la nueva representación sea máxima.
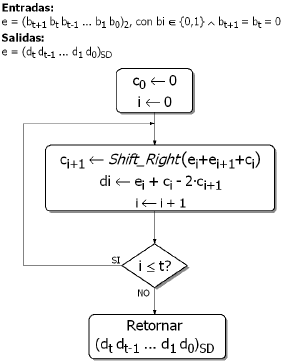
Figura 4. Algoritmo de recodificación del exponente
Figure 4. Exponent reconding algorithm
Es de anotar que el operador de recodificación de la figura 4 incrementa en un bit la longitud del número, respecto a la notación binaria tradicional. Como consecuencia de lo anterior, el algoritmo de Exponenciación Modular tomará una iteración adicional en su recorrido por la representación en dígito signado del exponente, desmejorando así el desempeño de la implementación. Más importante es el efecto que tiene la notación de dígito signado en la estructura del algoritmo binario de la figura 1. En el algoritmo original, se recorre el exponente un dígito binario a la vez, en caso que el dígito evaluado sea 1, se deberá calcular un producto modular adicional. Para el algoritmo modificado y de acuerdo con (5), un dígito de la representación del exponente puede tener tres valores: -1, 0 y 1. La aparición del dígito negativo plantea la necesidad de calcular condicionalmente una nueva operación llamada división modular, que básicamente equivale a calcular una división seguida de un módulo o residuo. La figura 5 muestra el algoritmo de Exponenciación modificado para manejar una notación de dígito signado para el exponente. La división modular está representada en la figura como P = P / X mod M.
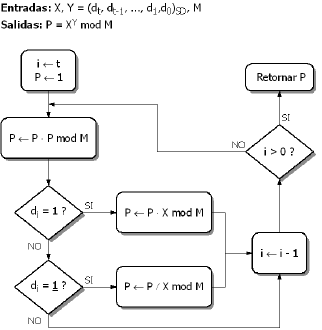
Figura 5. Algoritmo de Exponenciación Modular para exponente recodificado
Figure 5. Modular exponentiation algorithm with recoded exponent
En la versión original del algoritmo binario la única operación de complejidad importante que aparece es el producto modular. Un diseñador que desee calcular exponenciaciones de manera óptima debería preocuparse únicamente por optimizar el cálculo de productos modulares. Esta estrategia es la que más se encuentra reportada en implementaciones hardware de la exponenciación modular y de hecho existen varios algoritmos tendientes a mejorar el desempeño en el cálculo de un producto modular. Con la versión transformada del algoritmo aparece una nueva operación que debe ser optimizada. En entornos limitados en hardware como lo pueden ser las implementaciones en dispositivos reconfigurables, la optimización simultánea de los dos operadores es más compleja.
La ley de Amdahl sugiere que es inútil incurrir en esfuerzos de optimización excesivos tendientes a mejorar cierto aspecto de una solución hardware, si la fracción que ocupa este aspecto dentro de la totalidad del problema es mínima [14]. La figura 5 muestra que la ejecución de divisiones modulares es eventual y está condicionada a la aparición de dígitos negativos en la representación del exponente. En la figura 6 se muestran los resultados de una simulación expresando el porcentaje de operaciones que serían divisiones modulares en el cálculo de una exponenciación, usando el algoritmo transformado, para diferentes longitudes de bit. Como puede verse, la frecuencia de aparición de divisiones modulares en la ejecución del algoritmo se encuentra alrededor del 5% y tiende a saturarse para longitudes de bit considerables. Combinando esta información con la formulación aritmética de la ley de Amdahl, se llega a la conclusión de que en el mejor caso (es decir, si los esfuerzos de optimización lograrán reducir el tiempo de ejecución de una división modular a cero segundos exactos) el desempeño global de la Exponenciación Modular solo mejora en un 5.26 %. Es decir, se incurriría en un esfuerzo de diseño colosal que no se ve reflejado en la Mejora global de desempeño de manera significativa.
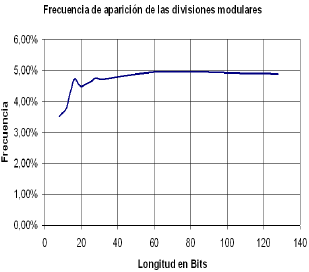
Figura 6. Frecuencia de aparición de divisiones modulares en una Exponenciación Modular con exponente recodificado
Figure 6. Modular division frecuency in a modular exponentation with recoded exponent
2.3 RNS
Los Sistemas de Numeración por Residuos o RNS (por las siglas en inglés de Residue Number Systems), permiten la distribución de cálculos entre números de gran tamaño sobre anillos modulares (o grupos finitos Zm), lo que permite una mejora en el desempeño de las soluciones. Esta característica es bien conocida y usada sobre todo en entornos de Procesamiento Digital de Señales y Criptografía.
La idea con los sistemas RNS es pasar de una representación modular que requiere una cantidad de bits considerable a otra en donde se tienen múltiples valores en distintos módulos para representar un solo número [15]. Cada uno de estos valores ocupa menos bits que la representación original y el hecho que sea independiente de los demás permite la implementación de operaciones de manera concurrente. La recombinación final de los resultados parciales puede llegar a ser bastante compleja y es función directa de cuántas bases o residuos se usen para representar los números. Las implementaciones software de sistemas RNS usan representaciones de hasta tres elementos para reducir la complejidad de las recombinaciones finales. Debido a esta misma razón, Se conocen muy pocas implementaciones hardware [16] que hagan uso de RNS, si bien se han hecho muchos estudios teóricos acerca del tema.
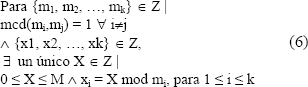
La ecuación (6) plantea la formulación matemática de los sistemas RNS a partir del teorema del residuo chino. Como puede verse, la idea es poder representar un número entero cualquiera X por medio de un conjunto de valores de menor longitud {x1, x2, , xk}. Este conjunto es referido como representación RNS o de raíz mixta del número X para los módulos {m1, m2, , mk}. Dado que las representaciones son ortogonales o independientes entre si, es posible aplicar las operaciones de manera independiente a cada uno de los elementos de la representación y luego recombinar los resultados parciales.
En resumen, con RNS se puede dividir el cálculo de cierta operación aritmética sobre números grandes (gran longitud en bits), en una serie de operaciones independientes entre sí, sobre las representaciones en raíz mixta de los operandos en cuestión. Como tales representaciones son de menor tamaño, las operaciones sobre ellas serán menos complejas y se podrán calcular en menor tiempo. Además, la naturaleza independiente de todos los números que componen una representación RNS permite inferir implementaciones concurrentes en hardware de las operaciones mencionadas.
Obsérvese también que (6) garantiza que la representación RNS de cierto número es única, de modo que existe una manera unívoca por medio de la cual se puede obtener cierto número X a partir de su representación en raíz mixta. La forma de recombinar los elementos de raíz mixta de una representación para obtener el valor del entero que representan es referida como algoritmo de Garner [8].
En entornos criptográficos, no siempre es posible tener disponibles todos los factores (m1, m2, , mk) que componen el módulo del sistema (M), de modo que no siempre se puede usar RNS en el cálculo de una exponenciación modular. En sistemas como RSA y ElGamal, por ejemplo, el conocimiento de los factores que componen el módulo provee a un criptoanalista con las herramientas para descifrar mensajes ajenos, suplantar entidades, etc.
Normalmente en estos sistemas, el conocimiento de los factores del módulo es exclusivo del usuario poseedor de la clave privada. De modo que una aproximación que use RNS en entornos criptográficos deberá usar un exponenciador para las operaciones de cifrado y otro muy distinto y potencialmente más lento para las operaciones de descifrado. Tal es el caso de la referencia [17], donde se hacen reportes de desempeño independientes para cifrado y descifrado en un entorno de firmas digitales RSA. Esta asimetría en las operaciones de cifrado y descifrado pudiera considerarse como la primera desventaja del uso de RNS en entornos criptográficos.
La implementación RNS a la que hace referencia este documento usa como bloques constitutivos Exponenciadores optimizados de 32 bits, usados de manera concurrente para el cálculo de exponenciaciones modulares con operadores de mayor tamaño. Esta aproximación es referida como máquina SIMD dentro de una taxonomía propuesta por Flynn y corresponde al nivel más elemental de paralelismo en un esquema de procesamiento [18].
3. RESULTADOS OBTENIDOS
La figura 7 muestra los resultados de la síntesis del operador Exponenciación Modular luego de haber sido sometidos al proceso de optimización referido anteriormente. Es un gráfico que muestra en un eje logarítmico los valores de la función de costo (f) para diferentes tamaños de los operandos (N).
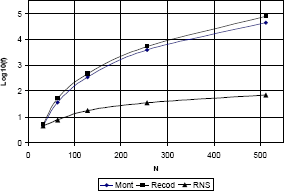
Figura 7. Comparación entre las tres alternativas para el Exponenciador Modular
Figure 7. Cost function comparison between tree choices for modular exponentiation
Los resultados parecen concluyentes: La implementación RNS de la Exponenciación Modular llega a ser superior a cualquiera de las otras dos alternativas hasta en dos órdenes de magnitud para la función de costo escogida. Adicionalmente, la diferencia en las funciones de costo se hace más contundente para valores de N, lo que constituye una situación deseable en entornos criptográficos.
Sin embargo, la implementación de Exponenciadores RNS en aplicaciones prácticas tiene algunas limitantes. En primer lugar, existe la asimetría entre las operaciones de cifrado y descifrado mencionada antes cuando se pretende llevar el Exponenciador RNS a entornos criptográficos. Adicionalmente, se deben considerar los detalles asociados a la recombinación de los resultados parciales, una vez se han calculado las Exponenciaciones Modulares sobre los L componentes de la representación en raíz mixta. El algoritmo propone la forma de llevar una serie de valores correspondientes a la representación en raíz mixta de cierto número a su representación binaria natural. Se requiere del cálculo de un total de L! inversos multiplicativos modulares para su implementación, si bien existen optimizaciones tendientes a reducir este valor [19].
Lamentablemente, el operador inverso multiplicativo modular es de naturaleza no determinística y las estimaciones de peor caso son demasiado pesimistas [20], además de ser poco probables en un entorno criptográfico.
Para poder hacer comparaciones de desempeño más justas, en donde se tenga en cuenta el tiempo que toma la recombinación de resultados parciales para la implementación RNS, se optó por hacer descripciones software de los algoritmos de Montgomery y RNS para cuando L=2 y L=4. La figura 8 muestra los resultados de tales descripciones, en donde se grafica el comportamiento del tiempo de ejecución para diferentes valores de N.
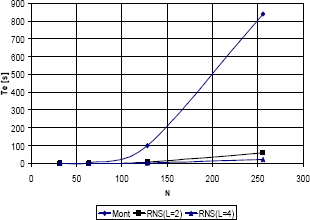
Figura 8. Resultados de una simulación software para la Exponenciación de Montgmoery y RNS
Figure 8. Software simulation results for Montgomerys and RNS exponentiations
La figura evidencia que cuando se introduce la recombinación de resultados al exponenciador RNS, las diferencias de desempeño no son tan acentuadas, si bien RNS sigue siendo la opción de mejor comportamiento. La discusión anterior sugiere que no es apropiado usar demasiados factores para la representación en raíz mixta de los operandos de la Exponenciación Modular. Dado que se requiere del cálculo de L! inversos multiplicativos modulares, existirá un valor de L para el cual la sobrecarga de la recombinación de los resultados sea tal que contrarreste los buenos resultados obtenidos al distribuir las operaciones sobre la representación en raíz mixta.
4. CONCLUSIONES
De todas las opciones disponibles para la implementación de la Exponenciación Modular se ha mostrado que la que usa recodificación del exponente es la que exhibe un comportamiento más pobre. De hecho, no se encuentran trabajos reportados sobre una implementación hardware que haga uso de representaciones de dígito signado para el exponente. De acuerdo con la discusión anterior, esto puede deberse a la necesidad de una serie de operadores de cierta complejidad, cuya optimización simultánea en un entorno hardware puede ser difícil. Se concluye que esta estrategia es más adecuada para entornos software, donde la implementación de tales operadores no representa grandes esfuerzos de diseño.
Se propone que la implementación RNS debe hacerse adoptando una estrategia de codiseño, donde las Exponenciaciones Modulares de la representación en raíz mixta se hagan concurrentemente en hardware, mientras que la recombinación posterior de los resultados sea desarrollada en software y ejecutada por un microprocesador de propósito general. En entornos en donde la disponibilidad de un microprocesador no sea posible, se plantea el uso del exponenciador de Montgomery, como un compromiso aceptable entre complejidad y desempeño.
REFERENCIAS
[1] RIVEST R. L, SHAMIR A, ADLEMAN L. A method for obtaining Digital Signatures and Public-key Cryptosystems. Communications of the ACM. 1978. [ Links ]
[2] RABIN M. O. Digitalized Signatures and Public Key Functions as Intractable as Factorization. Massachusetts Institute of Technology. Laboratory for Computer Science. 1979. [ Links ]
[3] ELGAMAL T. A public key cryptosystem and a signature scheme based on discrete logarithms. Lecture Notes in Comput. Sci., 196, Springer, Berlin, pages 10-18, 1985. [ Links ]
[4] SENDRIER N. MCEliece Public key Cryptosystems. Project CODES. INRIA RocQuencourt. 1996. [ Links ]
[5] LEVITIN A. Introduction to the Design and Analysis of Algorithms. Addison Wesley. 2002. ISBN: 0-201-74395-7. [ Links ]
[6] HORNER W. G. A new method of solving numerical equations of all orders, by continuous approximation. In Philosophical Transactions of the Royal Society of London, pp. 308-335, July 1819. [ Links ]
[7] CHIANG J, CHIEN C, CHEN J, CHOU H. An Efficient VLSI Architecture for Rivest-Shamir-Adleman Public-key Cryptosystem. Tamkang Journal of Science and Engineering, Vol. 7, No 4, pp. 241–250, 2004 [ Links ]
[8] MENEZES A, OORSCHOT P. V, VANSTONE S. Handbook of applied Cryptography. CRC Press. 1996. [ Links ]
[9] BOLAÑOS F, BERNAL A. Diseño y Optimización de un Multiplicador Modular usando Hardware Reconfigurable. VII Encuentro de Investigación sobre Tecnologías de la Información aplicadas a la solución de problemas EITI–2006. Agosto 2006. [ Links ]
[10] MONTGOMERY P. L. Modular Multiplication without trial division. Math. Of Computation. 44(70):519 – 521, April 1985. [ Links ]
[11] KOÇ Ç. K, ACAR T. Fast Software Exponentiation in GF(2k). IEEE Computer Society Press. Proceedings, 13th Symposium on Computer Arithmetic. pp. 225 – 231, 1997. [ Links ]
[12] HACHEZ G, QUISQUATER J. J. Montgomery Exponentiation with no Final Substractions: Improved Results. Lecture Notes in Computer Science. Vol. 1965. pp. 293 – 301. 2000. [ Links ]
[13] JOYE M, YEN S–M. Optimal Left–to–Right Binary Signed–Digit Recoding. IEEE Transactions on Computers. 49(7):740–748, 2000. [ Links ]
[14] HENNESSY J. PATTERSON D. Computer architecture: A quantitative approach. Morgan Kauffman Publishers. 2004. ISBN 1-55860-596-7. [ Links ]
[15] BAJARD J. C, PLANTARD T. RNS Bases and Conversions. LIRMM UMR 5506. University of Montpelier 2, France. [ Links ]
[16] CIET M, NEVE M, PEETERS E, QUISQUATER J. Parallel FPGA Implementation of RSA with Residue Number Systems. UCL Crypto Group. Belgium . 2003. [ Links ]
[17] BLUM T, PAAR C. Montgomery Modular Exponentiation on Reconfigurable Hardware. 14th IEEE Symposium on Computer Artihmetic. Apr. 14 – 16, 1999. [ Links ]
[18] STALLINGS W. Computer Organization and Architecture: Designing for Performance. Prentice Hall Computer Science. 2006. ISBN 0-13-185644-8. [ Links ]
[19] CIET M, NEVE M, PEETERS E, QUISQUATER J. Parallel FPGA Implementation of RSA with Residue Number Systems. UCL Crypto Group. Belgium . 2003. [ Links ]
[20] STEHLÉ D, ZIMMERMAN P. A Binary Recursive GCD Algorithm. LORIA/INRIA 2003. [ Links ]














