Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.75 n.156 Medellín set./dez. 2008
IDENTIFICACIÓN DE SISTEMAS DE EXCITACIÓN: ANÁLISIS DETALLADO DE METODOLOGÍA Y RESULTADOS
IDENTIFICATION OF EXCITATION SYSTEMS: DETAILED ANALYSIS OF METHODOLOGY AND RESULTS
HÉCTOR ANTONIO BOTERO
Grupo de Automática, Universidad Nacional de Colombia, habotero@unalmed.edu.co
JOSÉ MIGUEL RAMÍREZ
Grupo de Investigación en Control Industria, Universidad del Valle, jomiram@univalle.edu.co
Recibido para revisar Agosto 29 de 2007, aceptado Abril 11 de 2008, versión final Mayo 06 de 2008
RESUMEN: En este documento se presenta la descripción detallada de la metodología y los resultados obtenidos para la identificación de parámetros de modelos de sistemas de excitación del estándar IEEE std 421.5 de 1992, propuestos para estudios de estabilidad en sistemas de potencia. La metodología aplica técnicas de identificación paramétrica a las dinámicas lineales del modelo del sistema de excitación; para ello se aplican señales binarias pseudo aleatorias de pequeña magnitud, con operación del generador sincrónico fuera de línea, lo que permite reducir el tiempo de prueba de las máquinas con relación a métodos de respuesta al escalón o respuesta en frecuencia. Los parámetros restantes para las no linealidades como saturación de señal y saturación magnética en las excitatrices se obtienen de pruebas simples de excursión de gran señal. La metodología se ilustra aplicándola en simulación al modelo IEEE tipo ST1A, y experimentalmente a un sistema de excitación auto excitado directo digital, representado con el modelo IEEE tipo ST4B. Los resultados de simulación y experimentales muestran la validez de la metodología propuesta, lográndose porcentajes de aciertos del 96% en simulación y 74% en experimentación.
PALABRAS CLAVE: Identificación, sistemas de excitación, predictor de error, IEEE std 421.5.
ABSTRACT: This paper presents a detailed description of the methodology and results obtained for the parameters identification of excitation systems models defined in the IEEE standard 421,5, 1992 proposed for stability studies in power systems. The methodology applies parametric identification techniques to the linear dynamic of the excitation system model; for it, a small pseudo random binary signal is applied with the synchronous generator operating off line, which allows to reduce the testing time of the machines in relation to the step or frequency response methods. The remaining parameters for the non-linear components, as signal saturation and magnetic saturation in the exciters, are obtained from simple tests of great signal excursion. The methodology is illustrated in simulation by applying it to the IEEE ST1A model and experimentally to a self-excited digital excitation system, represented with the ST4B IEEE model. The experimental and simulation results show the validity of the proposed methodology, achieving success rates of 96% to 74% in simulation and experimentation.
KEYWORDS: Identification, excitation systems, predictor error, IEEE std 421.5.
1. INTRODUCCIÓN
Los sistemas de potencia modernos están constantemente sometidos a perturbaciones como cambios súbitos de carga y generación, fallas en equipos, reconfiguración de líneas de transmisión y redes de distribución, perturbaciones atmosféricas y ataques con material explosivo.
Adicionalmente la globalización de la economía y los convenios entre países vecinos ha impulsado las interconexiones de sistemas eléctricos, lo cual conlleva a que estos sistemas queden sometidos a perturbaciones adicionales y que se tenga una fuerte tendencia a llevar los equipos a sus límites operativos.
Debido a lo anterior, adquiere vigencia el modelado y la identificación de sistemas de excitación, porque la confiabilidad de los resultados arrojados por el análisis de sistemas de potencia depende en gran medida de la exactitud de los modelos.
Con el objetivo de obtener buenos modelos, varios investigadores alrededor del mundo han estudiado y aplicado métodos para identificar los parámetros de sistemas de excitación. Los primeros intentos para identificar parámetros de sistemas de excitación se realizaron con base en métodos de respuesta en el tiempo y respuesta en frecuencia; el objetivo era identificar parámetros dinámicos y estáticos [8, 9]. Posteriormente se utilizaron métodos basados en modelos autoregresivos, en los cuales se realizan aproximaciones lineales para los componentes no lineales del sistema [1, 10, 12, 13].
Con el fin de lograr identificar los parámetros de componentes lineales y no lineales simultáneamente se han utilizado métodos de trayectoria de sensibilidad y aproximación estocástica del gradiente promedio [4, 11]. Otros estudios tienden a utilizar pocas señales de entrada y a registrar pocas señales de salida para hacer más simple el método de identificación. La señal de entrada se inyecta en la referencia del sistema de excitación y la señal de salida se toma como el voltaje en bornes del generador sincrónico [5]. Con el fin de considerar el ruido en el proceso de identificación y minimizar su efecto en el resultado, se ha trabajado con métodos basados en la transformada rápida de Fourier y en mínimos cuadrados generalizados [2, 3]. Finalmente, algunos trabajos tienden a hacer más simple el proceso de identificación realizando aproximaciones de los componentes no lineales, utilizando programas de computador que permitan simplificar los cálculos e inyectando pocas señales en el proceso de identificación [6, 7, 14].
Sin embargo, los métodos que se acaban de describir tienen inconvenientes ya que son matemáticamente complejos y utilizan técnicas que no son de manejo común en nuestra industria. Adicionalmente los documentos que reportan los resultados no son lo suficientemente explicativos para que personal no experto pueda utilizarlos de manera simple. En los reportes no se explican las ayudas computacionales para resolver las ecuaciones resultantes y se supone que se tiene la experiencia suficiente para realizar este trabajo, excepto lo reportado en [14], donde se describe un programa amigable y de fácil utilización para la identificación de parámetros del generador sincrónico y el sistema de excitación. Sin embargo, a nuestro conocimiento, no se han reportado en el país experiencias con este tipo de aplicaciones.
En algunos artículos sólo se estiman pocos parámetros mientras otros se dejan fijos o se suponen conocidos. Esto reduce la exactitud del modelo debido a que los parámetros fijos se basan en datos de fabricante, que normalmente tienen rangos de variación muy amplios.
De otro lado no se da una descripción clara de las pruebas realizadas, ni del equipo utilizado en la ejecución de las mismas, lo cual limita la aplicación en nuestro medio.
Adicionalmente, algunos autores utilizan la discretización de los modelos con base en aproximaciones numéricas como la transformación bilineal. Estas aproximaciones añaden limitantes al proceso de obtención de parámetros, porque no es fácil hacer la interpretación de los resultados en el dominio discreto (transformada Z), con parámetros que no coinciden con elementos físicos del sistema real como ganancias, constantes de tiempo y limitadores en los componentes.
Con base en la problemática anterior, y con el objetivo de proponer una herramienta que permita obtener los parámetros de sistemas de excitación de forma simple, en este artículo se presenta una metodología que se aplica a dos tipos de sistemas ST1A y ST4B de [15], que son los más comúnmente encontrados en el Sistema Interconectado Nacional. El propósito de este documento es analizar en forma detallada la metodología para obtener los resultados mostrados en [16]. La aplicación de dicha metodología se hace en los casos ST1A a nivel de simulación y en un sistema real a escala de laboratorio representado por un modelo ST4B modificado. Las particularidades de cada caso se describen con alto grado de detalle con el fin de mostrar algunas consideraciones que se deben tener en cuenta. Al final se hace una evaluación de los procedimientos propuestos con base en la experiencia adquirida.
La metodología puede ser estudiada y aplicada por Ingenieros con algunos conocimientos en sistemas de potencia, modelado e identificación de sistemas dinámicos, simulación y manejo del programa Matlab.
2. METODOLOGÍA PROPUESTA
El procedimiento propuesto se basa en dos enfoques:
- Metodología de pruebas realizadas en el sistema de control de excitación de la central de Salvajina y reportada en [17-18]. La metodología se basa en la determinación de las ganancias, constantes de tiempo, límites y demás parámetros con base en la estructura del modelo, las ecuaciones diferenciales que rigen el comportamiento del mismo y las señales previamente medidas; este enfoque se aproxima a lo que se conoce como enfoque de ¨caja blanca¨. En general se utilizan pruebas de pequeña señal y gran señal, estas últimas para determinar los límites de los elementos involucrados en el modelo.
- Metodología de identificación paramétrica con una estructura de modelo predeterminada. Con esta metodología se propone un modelo para el sistema con base en las normas y las recomendaciones del fabricante. Con el modelo propuesto se obtiene una representación lineal en variables de estado del sistema dinámico, se eligen los parámetros a identificar y mediante la aplicación de una técnica de identificación de sistemas, se obtienen los parámetros del modelo.
A continuación se explican los pasos de la metodología.
2.1 Obtención del modelo matemático del sistema
Inicialmente se selecciona una estructura para el modelo matemático. Esta estructura se puede obtener de la norma [15] para los sistemas de excitación. Los modelos en la norma se describen mediante diagramas de bloques, de los cuales se obtienen las ecuaciones diferenciales que representan el sistema físico. Estas ecuaciones son normalmente no lineales debido a la saturación magnética de las excitatrices y límites en los elementos electrónicos.
2.2 Definición y medición de alinealidades
La identificación de la función de saturación se realiza midiendo las entradas y salidas del generador en dos puntos de operación, con y sin saturación [15]. Para la identificación de las alinealidades tipo límites, se pueden aplicar señales de gran magnitud en las tarjetas electrónicas de los reguladores, o señales periódicas de gran amplitud y alta frecuencia que saturen transitoriamente las variables de interés [17-18]. Este tipo de pruebas se conocen como pruebas de gran señal. Cada prueba se especifica según el equipo y los manuales del fabricante. Los resultados obtenidos en la medición de los límites deben ser llevados a la base en que se quiera representar el sistema de excitación para el manejo por unidad.
2.3 Linealización del modelo en el punto de operación
Los modelos de sistemas de excitación deben ser linealizados porque los métodos de identificación que se aplicarán suponen que el sistema es lineal.
Los límites pueden ser eliminados si se considera que los cambios en el sistema no tienen magnitudes apreciables que los superen. La función de saturación es diferenciable y se puede linealizar alrededor de un punto de operación.
Mediante la linealización es posible obtener la representación en variables de estado estándar para sistemas lineales invariantes:
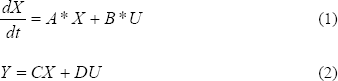
2.4 Obtención de la dinámica general del sistema
Un paso importante en el proceso de identificación consiste en preparar y ejecutar un experimento que permita obtener información sobre la dinámica total del sistema. Para ello es necesario realizar una prueba escalón al sistema real para estimar el tiempo de establecimiento 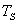 del mismo. Esta prueba se realiza inyectando un cambio de escalón en el voltaje de referencia y registrando la dinámica del voltaje de salida del generador sincrónico en vacío. La magnitud del escalón debe ser tal que no se exciten apreciablemente las no linealidades en el sistema.
del mismo. Esta prueba se realiza inyectando un cambio de escalón en el voltaje de referencia y registrando la dinámica del voltaje de salida del generador sincrónico en vacío. La magnitud del escalón debe ser tal que no se exciten apreciablemente las no linealidades en el sistema.
2.5 Cálculo de la señal de entrada
Los métodos de identificación paramétrica exigen que la señal de entrada aplicada sea de excitación persistente para [19]:
- Obtener una estimación consistente e insesgada y evitar soluciones singulares,
- Obtener una variación permanente pero con una correlación muy baja,
- Excitar las dinámicas importantes del sistema en el rango de frecuencias de interés para la aplicación del modelo.
Para cumplir lo anterior se utiliza una Secuencia Binaria Pseudo Aleatoria (SBPA). La SBPA es una señal de dos niveles consistente en una sucesión de impulsos rectangulares modulados en su ancho, de forma que esta se aproxime a un ruido blanco con un contenido rico de frecuencias. La SBPA es periódica, determinística y se puede generar por medio de un registro de desplazamiento con suma en módulo 2 [19].
La SBPA se caracteriza por tres parámetros:
- El nivel de la señal
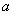 , que determina el valor máximo y mínimo de la misma.
, que determina el valor máximo y mínimo de la misma. - El número de registros
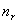 , que determina la longitud
, que determina la longitud 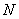 de la señal.
de la señal. 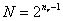 .
. - El período del reloj
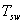 , mediante el cual se modifica la duración de la señal y su densidad espectral de potencia
, mediante el cual se modifica la duración de la señal y su densidad espectral de potencia
La selección de 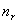 y
y 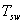 se puede realizar considerando que el espectro de potencia de la SBPA está determinado por [20]:
se puede realizar considerando que el espectro de potencia de la SBPA está determinado por [20]:
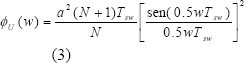
donde 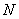 es la longitud de la SBPA y
es la longitud de la SBPA y 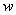 es la frecuencia en (rad/s).
es la frecuencia en (rad/s).
El ancho de banda del espectro de potencia es alcanzado en el valor:

En la frecuencia 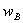 la señal alcanza la mitad del valor máximo de la densidad espectral de potencia. Debido a lo anterior y a la periodicidad de la función de covarianza de la SBPA, el rango útil de esta señal está entre:
la señal alcanza la mitad del valor máximo de la densidad espectral de potencia. Debido a lo anterior y a la periodicidad de la función de covarianza de la SBPA, el rango útil de esta señal está entre:
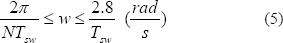
Ahora bien, la duración del pulso más ancho de la SBPA es 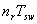 y la duración de este pulso debe ser aproximadamente igual al tiempo de establecimiento del sistema
y la duración de este pulso debe ser aproximadamente igual al tiempo de establecimiento del sistema 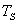 , con el fin de determinar correctamente la ganancia estática del mismo [21]. Un procedimiento para calcular la SBPA puede ser:
, con el fin de determinar correctamente la ganancia estática del mismo [21]. Un procedimiento para calcular la SBPA puede ser:
- Determine el tiempo de establecimiento del sistema
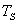 .
. - Con base en la información a priori del sistema, estime la banda de frecuencias de interés.
- Considere fijo
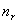 (por ejemplo
(por ejemplo 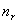 =8) y con base en esto calcule el
=8) y con base en esto calcule el 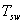 como:
como:

- Verifique que la banda de frecuencias de interés quede cubierta con la selección de
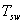 , para ello utilice la ecuación (5).
, para ello utilice la ecuación (5). - Verifique que el tiempo de muestreo sea múltiplo del
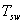 (se recomienda
(se recomienda 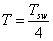 ).
). - Verifique que se cumplen todos los criterios, de lo contrario cambie
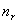 y/o
y/o 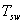 y repita.
y repita. - Para la determinación de la magnitud de la SBPA se deben verificar dos criterios explicados antes:
- La magnitud debe ser tal que no se deben excitar apreciablemente las no linealidades como límites y restricciones físicas, ni tampoco poner en peligro la operación del equipo.
- La relación señal ruido debe ser alta. Esto se puede verificar observando el registro de las señales.
Algunas consideraciones que se deben tener en cuenta para seleccionar el tiempo de muestreo 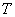 son [22]:
son [22]:
- El tiempo de muestreo
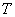 se selecciona considerando un compromiso entre la reducción del ruido y la captura de las dinámicas rápidas del sistema.
se selecciona considerando un compromiso entre la reducción del ruido y la captura de las dinámicas rápidas del sistema. - Si el tiempo de muestreo es muy pequeño se pueden generar problemas numéricos en los algoritmos debido al ruido introducido.
- Si el tiempo de muestreo es muy grande comparado con las constantes de tiempo del sistema, se tendrán errores de varianza en la identificación.
- Para seleccionar el tiempo de muestreo se debe tener en cuenta que la constante de tiempo más pequeña del sistema de excitación (
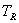 ) se encuentra en el filtro del circuito de medición del voltaje en terminales. Esta constante de tiempo tiene un valor típico de 20 ms, lo cual sugiere que el tiempo de muestreo debe ser mínimo de 10 ms, de tal forma que se capturen 10 muestras en la respuesta dinámica de este filtro y no se pierda información en el proceso de toma de datos.
) se encuentra en el filtro del circuito de medición del voltaje en terminales. Esta constante de tiempo tiene un valor típico de 20 ms, lo cual sugiere que el tiempo de muestreo debe ser mínimo de 10 ms, de tal forma que se capturen 10 muestras en la respuesta dinámica de este filtro y no se pierda información en el proceso de toma de datos.
2.6 Aplicación del método predictor de error
Luego de tener los registros de entrada y salida se encuentran los parámetros relacionados con las dinámicas lineales mediante la aplicación del Método Predictor de Error. Con la utilización de este método se obtienen los estimativos de los parámetros y sus posibles desviaciones. Adicionalmente se puede encontrar un valor que indique el error en el proceso de identificación.
Mediante el método predictor de error se trata de determinar el vector de parámetros 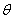 , tal que el error de predicción:
, tal que el error de predicción:
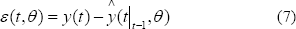
sea pequeño, donde 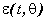 es el error de predicción,
es el error de predicción, 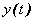 es la salida medida,
es la salida medida, 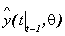 es la predicción de
es la predicción de 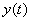 con valores pasados, y
con valores pasados, y 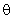 es el vector de parámetros a ser estimados. Para aplicar el método se considera que el sistema puede tomar la forma de estructura de modelo general:
es el vector de parámetros a ser estimados. Para aplicar el método se considera que el sistema puede tomar la forma de estructura de modelo general:
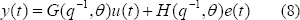
donde 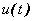 es la entrada,
es la entrada, 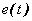 es una secuencia independiente, aleatoria, con media cero (ruido blanco) y
es una secuencia independiente, aleatoria, con media cero (ruido blanco) y 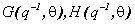 son filtros de dimensión finita con
son filtros de dimensión finita con 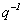 como el operador retardo tal que se puede construir un predictor lineal de la forma:
como el operador retardo tal que se puede construir un predictor lineal de la forma:
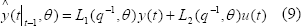
que se calcula con datos pasados y filtros predictores 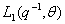 y
y 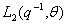 .
.
El predictor de la ecuación (9) se puede construir de varias formas para el modelo de la ecuación (8). Como el modelo y el predictor son dados, el error de predicción se calcula con (7) para todos los datos. Finalmente el valor estimado de 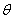 es obtenido tal que el error:
es obtenido tal que el error:
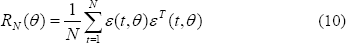
sea pequeño.
El proceso se ilustra en la Figura 1.
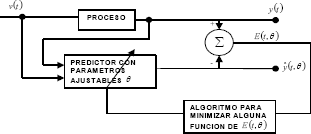
Figura 1. Proceso de identificación
Figure 1. Process for identification
2.7 Herramientas para la identificación
El proceso de identificación se simplifica utilizando una herramienta implementada en Matlab mediante la ayuda del módulo System Identification. La herramienta tiene una serie de funciones programadas que sirven para realizar la siguiente secuencia de operaciones:
- Carga archivo de datos, es decir los datos registrados en un osciloscopio.
- Organiza y filtra los datos, removiendo los valores medios y filtrando el ruido en los mismos. Adicionalmente separa datos para identificación y datos para validación.
- Aplica método predictor de error, mediante un modelo del sistema en variables de estado.
- Realiza proceso de validación, comparando gráficamente los resultados. Adicionalmente, entrega el porcentaje de aciertos y el análisis de correlación de los residuos con la entrada.
3. RESULTADOS OBTENIDOS EN SIMULACIÓN
La metodología de identificación se probó en simulación para un sistema de excitación estático cuyos parámetros se midieron en una planta real [18]. El sistema se representa mediante el modelo ST1A de [15]. Los registros se obtuvieron de datos arrojados por simulaciones realizadas en Matlab - Simulink. En el proceso de identificación se utilizaron dos programas de computador: uno que contiene los parámetros y otro que genera los datos. A continuación se explican estos programas.
Programa de parámetros:
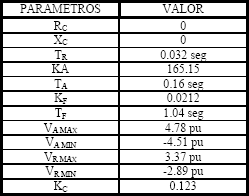
Este programa contiene los parámetros que necesita el simulador para reproducir la dinámica del sistema de excitación. Los parámetros utilizados se ilustran en la Tabla 1.
Tabla 1. Parámetros sistema ST1A
Table 1. Parameters system ST1A
Programa de simulación en Simulink:
Los datos para el proceso de identificación se obtienen de la simulación del sistema de control de excitación. El simulador incorpora funciones que permiten verificar la identificación del sistema con SBPA y considera dos tipos de señales de ruido en la medición: Ruido aleatorio (blanco) y ruido de 360 Hz presente en el puente de tiristores. El diagrama de simulación se muestra en la Figura 2.
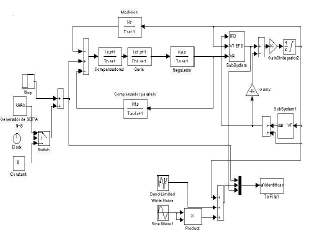
Figura 2. Simulador para el sistema ST1A
Figure 2. ST1A simulator system
El simulador se implementa de forma que
Modelado del sistema
El modelo del sistema se obtiene desde la referencia [15] y se linealiza alrededor del punto de operación. Los elementos del modelo son:

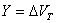
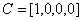
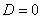
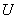 : Cambio en el voltaje de referencia
: Cambio en el voltaje de referencia 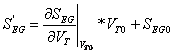
donde:
: Ganancia del regulador
: Ganancia de la red de estabilización
: Ganancia del circuito de medición
: Constante de tiempo del regulador
: Constante de tiempo de la red de estabilización
: Constante de tiempo del circuito de medición
: Constante de tiempo transitoria del campo
: Resistencia de campo
: Voltaje de campo
: Voltaje de salida del circuito de medición
: Voltaje de salida de la red de estabilización
: Voltaje de referencia
: Voltaje en terminales del generador sincrónico
: Función de saturación del generador
: Punto de operación para
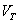
: Función de saturación del generador evaluada en
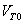
Realizando un análisis en la Matriz A de las ecuaciones anteriores se puede observar que los parámetros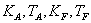 se pueden obtener independientemente mediante una técnica de identificación lineal. Para completar los parámetros del modelo, las constantes que tienen que ver con la regulación, el filtro de medición, la saturación y las constantes del campo del generador sincrónico se pueden medir con pruebas estándar.
se pueden obtener independientemente mediante una técnica de identificación lineal. Para completar los parámetros del modelo, las constantes que tienen que ver con la regulación, el filtro de medición, la saturación y las constantes del campo del generador sincrónico se pueden medir con pruebas estándar.
Identificación de no linealidades
Las no linealidades en este sistema están representadas por la función de saturación del generador sincrónico y los límites del regulador.
La función de saturación se determinó con base en la curva de vacío del generador como se explicó en la parte 2. Los valores de los límites del regulador 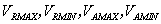 se obtienen mediante pruebas de gran señal como se explica en [17-18] u otras pruebas que permitan aumentar y disminuir la entrada al regulador hasta alcanzar los valores límite. Es necesario recordar que estos valores se deben llevar al sistema por unidad en las bases correspondientes.
se obtienen mediante pruebas de gran señal como se explica en [17-18] u otras pruebas que permitan aumentar y disminuir la entrada al regulador hasta alcanzar los valores límite. Es necesario recordar que estos valores se deben llevar al sistema por unidad en las bases correspondientes.
Identificación de la dinámica lineal
La medición del factor de reducción del voltaje de campo 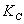 se puede lograr a partir de la ecuación aproximada del puente rectificador. Las pruebas a realizar se describen en [17-18]. El valor de la ganancia
se puede lograr a partir de la ecuación aproximada del puente rectificador. Las pruebas a realizar se describen en [17-18]. El valor de la ganancia 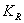 y la constante de tiempo del circuito de medición
y la constante de tiempo del circuito de medición 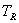 se pueden obtener mediante métodos tradicionales de respuestas al escalón aplicadas a estos subsistemas [23].
se pueden obtener mediante métodos tradicionales de respuestas al escalón aplicadas a estos subsistemas [23].
Así mismo es necesario conocer la constante 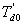 y la resistencia de campo
y la resistencia de campo 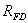 del generador sincrónico. Estos valores se pueden obtener mediante pruebas experimentales o desde datos suministrados por el fabricante.
del generador sincrónico. Estos valores se pueden obtener mediante pruebas experimentales o desde datos suministrados por el fabricante.
Los valores de las constantes 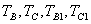 se suponen iguales a uno o cero según el simulador a utilizar. Esto es posible ya que los sistemas de excitación tienen circuito compensador en serie o en paralelo. En este trabajo se supone que la compensación se realiza a través de una red en paralelo con parámetros
se suponen iguales a uno o cero según el simulador a utilizar. Esto es posible ya que los sistemas de excitación tienen circuito compensador en serie o en paralelo. En este trabajo se supone que la compensación se realiza a través de una red en paralelo con parámetros 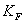 y
y 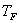 los cuales se determinan mediante el método de identificación.
los cuales se determinan mediante el método de identificación.
Tiempo de establecimiento del sistema
Para obtener el tiempo de establecimiento 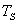 del sistema, se lleva el generador en vacío al punto de operación con
del sistema, se lleva el generador en vacío al punto de operación con 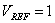 y se aplica un cambio del 1%. Los resultados se muestran en la Figura 3.
y se aplica un cambio del 1%. Los resultados se muestran en la Figura 3.
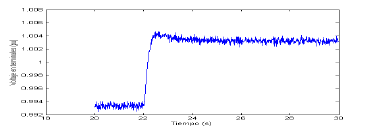
Figura 3. Respuesta al escalón del sistema ST1A
Figure 3. ST1A system step response
Con base en la respuesta al escalón se obtiene que el tiempo de establecimiento es de 4 s, Por lo tanto 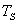 =4 .
=4 .
Cálculo de la señal de entrada
El rango de frecuencias de interés para los modelos de sistemas de excitación está entre 0 y 3 Hz es decir 0 a 18.8 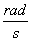 [15]. Con
[15]. Con 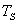 =4 y
=4 y 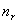 =8, se calcula el período del reloj de la SBPA como:
=8, se calcula el período del reloj de la SBPA como:

La banda de frecuencias de la SBPA se verifica con la ecuación:

En este caso con 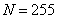 , se tiene que:
, se tiene que:
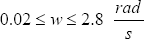
Aunque no se cumple con el rango máximo de frecuencias, la señal fue adecuada para la identificación. La amplitud de la señal SBPA variará entre 0.01 y –0.01, es decir un cambio del 1% alrededor del punto de operación; se ha verificado previamente que con este cambio no se exceden los límites impuestos.
Realización de la prueba y toma de datos
La simulación se realiza durante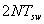 , es decir 500 s que corresponde a aproximadamente el doble del período de la SBPA. Los resultados de los datos obtenidos se observan en la Figura 4. No se observan los 500 s debido a que se eliminan los transitorios iniciales. El tiempo de muestreo se tomó en 10 ms para realizar una aproximación conservativa.
, es decir 500 s que corresponde a aproximadamente el doble del período de la SBPA. Los resultados de los datos obtenidos se observan en la Figura 4. No se observan los 500 s debido a que se eliminan los transitorios iniciales. El tiempo de muestreo se tomó en 10 ms para realizar una aproximación conservativa.
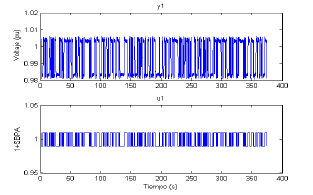
Figura 4. Datos registrados ST1A
Figure 4. ST1A registered data
Archivo de datos y parámetros iniciales
El archivo de datos contiene la información del tiempo, la entrada y la salida con estas dos últimas en por unidad y por lo tanto no es necesario un tratamiento especial de conversión. El archivo de parámetros iniciales se elabora de acuerdo con los valores que se prevean tienen los parámetros a identificar o con ayuda de valores extraídos desde información técnica.
Modelo lineal discretizado
El archivo que se genera para discretizar el modelo del sistema de excitación se realiza utilizando una M Function de Matlab. El archivo contiene la representación en variables de estado del sistema parametrizada en los parámetros desconocidos.
Cálculo de parámetros con el método predictor de error
Para realizar esto se ejecuta el programa de identificación y se obtienen los resultados de las Figuras 5 a 7. Con este programa se realiza la estimación de parámetros utilizando el método predictor de error y se hace la validación del modelo. En la ejecución del programa se hace inicialmente un tratamiento de los datos, que consiste en dividir los datos (identificación – validación), filtrarlos y eliminarles el valor medio. Este tipo de partición permite verificar de una forma más rigurosa la capacidad del modelo para reproducir datos.
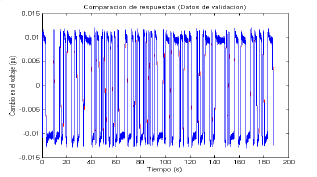
Figura 5. Comparación datos de validación ST1A
Figure 5. Comparison with ST1A validation data
Obtención de parámetros y validación del modelo
La validación del modelo se puede realizar con ayuda de las Figuras 5 a 7. En la Figura 5 se comparan la respuesta del modelo y la del sistema real ante la misma entrada, utilizando los datos de validación. Debido a que la comparación se hace difícil y no cuantificable, se calcula el porcentaje de aciertos que indica el porcentaje de datos que el modelo es capaz de reproducir. En este caso el porcentaje de aciertos es del 96%.
Adicionalmente en la Figura 6 se muestra la función de correlación de los residuos y la correlación entre los residuos y la entrada. Las líneas de demarcación indican los intervalos de confianza de estas funciones. Lo ideal es que ningún punto salga de estas franjas, sin embargo la correlación de los residuos es muy dependiente del tipo de entrada introducida y por ello no se considera determinante en la validación.
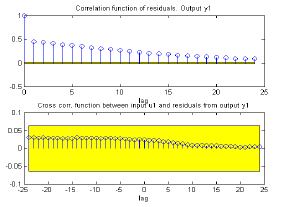
Figura 6. Funciones de correlación ST1A
Figure 6. ST1A correlation functions
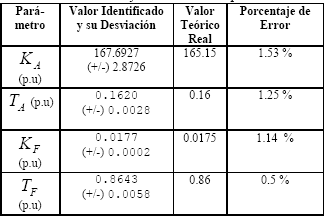
Finalmente se entregan los parámetros y sus desviaciones típicas. Para este caso los valores obtenidos son mostrados en la Tabla 2.
Tabla 2. Parámetros identificados sistema ST1A
Table 2. ST1A system identified parameters
Adicionalmente se hace una validación comparando la señal del voltaje de campo medida con la señal de voltaje de campo que entrega un simulador. Los parámetros utilizados por el simulador son los calculados en el proceso de identificación.
La entrada al simulador es la misma entrada medida. Esta comparación es importante porque la dinámica del voltaje de campo tiene una variación rápida. Los resultados de la comparación se observan en la Figura 7.
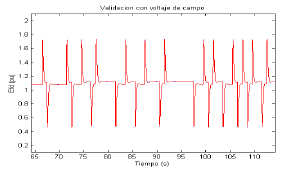
Figura 7. Comparación de señales de voltaje de campo ST1A
Figure 7. ST1A Field voltage signal comparison
En este caso se observa que los resultados son muy buenos, se tiene una buena coincidencia al comparar los gráficos, adicionalmente el porcentaje de aciertos es alto y por lo tanto los parámetros identificados son aceptados. Debido a que se trabaja con datos de un simulador es posible verificar que la desviación de los parámetros identificados respecto a los parámetros verdaderos es muy pequeña.
La comparación de las señales de campo permite analizar la capacidad del modelo para generar señales intermedias. En este caso las señales casi coinciden exactamente.
4. RESULTADOS OBTENIDOS EN UN CASO REAL
Con el objetivo de verificar la metodología en un caso real, se realizaron pruebas a un sistema de excitación construido en la Universidad del Valle [24]. El sistema contiene los siguientes elementos:
- Un generador sincrónico de 3 KVA, 8 A, 208 V, conexión delta, f.p. 0.7-1, 1800 rpm.
- Un motor primario, que consiste en un motor sincrónico de 216V, conexión delta, 15.5 A, 5Kw, f.p. =1, alimentado desde la red.
- Un actuador o excitatriz, que consiste en un puente monofásico totalmente controlado.
- Un regulador de voltaje implementado en un DSP (Digital Signal Processing) serie TMS 320C6711 de Texas Instrument. En este procesador se programó el algoritmo de control utilizando lenguaje C para implementar las ecuaciones en diferencia obtenidas del diseño.
Obtención del tiempo de establecimiento del sistema
Con el objetivo de obtener una idea sobre la dinámica general del sistema se realizó un experimento introduciendo un cambio desde el DSP. El sistema de control de excitación es autoexcitado y por lo tanto no es adecuado obtener una respuesta en lazo cerrado porque se tendría una realimentación positiva al aplicar un escalón o cambio del ángulo de disparo del puente rectificador. Con el aumento del ángulo de disparo, aumenta el voltaje en terminales y como el actuador se alimenta desde este, se produce de nuevo un incremento del voltaje en terminales y en el voltaje de campo. Por lo tanto la dinámica general se obtiene en lazo abierto.
El experimento involucra tener un voltaje AC fijo alimentando el puente monofásico totalmente controlado. A los tiristores del puente se les aplica un cambio en el ángulo de disparo desde el sistema digital, lo que implica un escalón en el voltaje de campo. Esta variación de la excitación produce un cambio del voltaje en terminales como se muestra en la Figura 8. El escalón de voltaje representa una variación de 10% sobre el voltaje nominal de la planta.
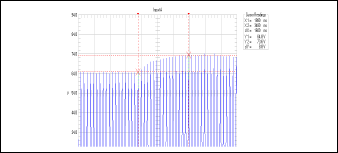
Figura 8. Respuesta al escalón del sistema ST4B
Figure 8. ST4B System step response
Con base en la respuesta al escalón se obtiene que el tiempo de establecimiento es de aproximadamente 1.2 segundos y la constante de tiempo es de 0.315 s. Con esta información y con los datos obtenidos de la prueba de vacío se obtienen los parámetros del generador, recordando que la constante de tiempo 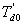 se puede calcular de la ecuación:
se puede calcular de la ecuación:
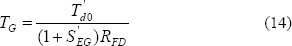
Cálculo de la señal de entrada
Con 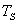 =1 s (aproximado desde 1.2 s) y
=1 s (aproximado desde 1.2 s) y 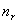 =8, se calcula:
=8, se calcula:
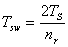 =0.25s
=0.25s
La banda de frecuencias de la SBPA es:
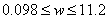
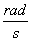
Aunque no se cumple con el rango máximo de frecuencias, la señal fue adecuada para la identificación. La amplitud de la señal SBPA varia entre 0.04 y –0.04, es decir un 4 % alrededor del punto de operación; se ha verificado previamente que con este cambio no se exceden los límites impuestos.
Realización de la prueba y toma de datos
Los resultados de los datos obtenidos se observan en la Figura 9. El tiempo de muestreo es de 50 ms.
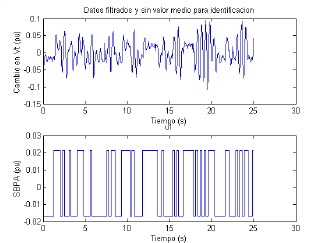
Figura 9. Datos registrados sistema ST4B
Figure 9. ST4B system registered data
Archivo de datos y parámetros iniciales
El archivo de datos contiene la información en p.u. El archivo de parámetros iniciales contiene los estimativos iniciales.
Modelo lineal discretizado
Luego de realizar varias pruebas, el modelo fue una simplificación de lo reportado en [25]. El diagrama en bloques del modelo se muestra en la Figura 10, pero con 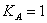 y
y  .
.
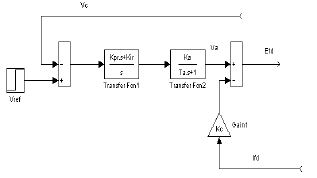
Figura 10. Modelo ST4B simplificado
Figure 10. ST4B simplified model
Cálculo de parámetros con el método predictor de error
El programa es igual al caso ST1A. Los resultados arrojados se muestran en la Tabla 3.
Tabla 3. Parámetros identificados sistema ST4B
Table 3. Identified parameters ST4B System

Validación del modelo
La validación del modelo se puede realizar con ayuda de las Figuras 11 y 12.
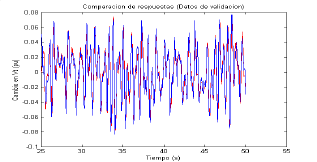
Figura 11. Comparación con datos de validación
Figure 11. Comparison with validation data
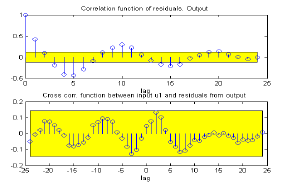
Figura 12. Funciones de correlación ST4B
Figure 12. ST4B correlation functions
El porcentaje de aciertos en este caso es del 74%.
En este caso no se validó el modelo con el voltaje de campo porque no se pudo medir esta señal.
5. CONCLUSIONES
Se ha propuesto una metodología para la identificación de sistemas de excitación la cual se realiza en dos fases: identificación de no linealidades, con métodos clásicos y sugeridos en normas internacionales, e identificación de dinámicas lineales, mediante el método predictor de error.
Una ventaja de la metodología es que sólo utiliza una señal de excitación persistente sumada a la señal de referencia para excitar las dinámicas del sistema. La señal de excitación persistente puede ser introducida en el algoritmo de control del sistema de excitación, si este es digital, o mediante la conmutación programada de una resistencia, si este es analógico.
La metodología propuesta incluye programas implementados en Matlab que contienen las funciones necesarias y recomendadas para realizar el proceso de identificación de forma ágil, lo cual simplifica el manejo matemático.
La metodología fue probada en varios sistemas de excitación, tanto en simulación como en un caso real, y los resultados fueron siempre satisfactorios.
AGRADECIMIENTOS
Los autores expresan su agradecimiento a Martha Lucía Orozco Gutiérrez, Ingeniera Electrónica, M.Sc, por los datos obtenidos en el banco experimental para el análisis del caso ST4B.
REFERENCIAS
[1] LIAW C. M. et al. Parameter Estimation of Excitation Systems from Sampled Data. IEEE Transactions on Automatic Control, May 1992. [ Links ]
[2] LIU C. S. et al. Identification of Exciter Constants Using a Coherence Function Based Weighted Least Squares Approach. IEEE Transactions on Energy Conversion. Sep 1993. [ Links ]
[3] GUO T. Y. et al. Identification of Model Parameters of Excitation Systems and PSS of Mingtan 6 via Finalization Fiels Test. IEEE Trans. on Power Systems, May 1995. [ Links ]
[4] WANG J. C. et al. Identification of Excitation Systems Models Based on Line Digital Measurements. IEEE Transactions on Power Systems, Ago 1995. [ Links ]
[5] HSU Y. T. et al. Experience With the Identification and Tuning of Excitation Systems Parameters at the Second Nuclear Power Plant of Taiwan Power Company. IEEE Trans, on Power Systems, May 1996. [ Links ]
[6] LUDWIG E. et al. A Feasibility Study of On Line Excitation System Parameters Estimation. IEEE Transactions on Power Systems, Ago 1998. [ Links ]
[7] BHASKAR R. et al. Nonlinear Parameter Estimation Of Excitation System. IEEE Transactions on Power Systems, Nov 2000. [ Links ]
[8] GIBBARD M. J. et al. Identification of Excitation System Parameters. IEEE Transactions on Power Apparatus and Systems, Jul/Ago1975. [ Links ]
[9] WARCHOL E. J. et al. Alinement and Modeling of Hanford Excitation Control for Sytem Damping. IEEE Transactions on Power Apparatus and Systems, mar/apr 1971. [ Links ]
[10] SANCHEZ J. J. et al. Trayectory Sensitivity Based Identification of Synchronous Generator and Excitation Systems Parameters. IEEE Transactions on Power Systems, Nov 1988. [ Links ]
[11] BENCHLUCH S. M. et al. 1993. A Trayectory Sensitivity Method for the Identification of Nonlinear Excitation System Models. IEEE Transactions on Energy Conversion, Jun 1993. [ Links ]
[12] BOLLINGER K. E. et al. A Method for On-Line Identification of Power Systems Model Parameters in the Presence of Noise. IEEE Transactions on Power Apparatus and Systems, Sep 1982. [ Links ]
[13] SMITH J. R. et al. 1993. Transfer Function Identification in Power Systems Applications. IEEE Transactions on Power Systems, Ago 1993. [ Links ]
[14] FELTES J. W. et al. Deriving Model Parameters from Field Test Measurements. IEEE Computer Applications in Power, Oct 2002. [ Links ]
[15] IEEE Std 421.5. Recommended Practice for Excitation System Models for Power System Stability Studies. 1992. [ Links ]
[16] BOTERO, H; RAMÍREZ, J.M. Identification of excitation systems – Methodology and Results. International Conference on Industrial Electronics and Control Application. Quito (2005). [ Links ]
[17] RAMIREZ, J. M. et al. Modelos Matemáticos para los Reguladores de Velocidad y los Sistemas de Excitación de la Planta de Salvajina. Energía y Computación. No 2, 2000. [ Links ]
[18] SAAVEDRA, A. J. Modelado Para Estudios de Estabilidad de los Sistemas de Control Velocidad y Excitación de la Central de Salvajina. Tesis de Maestría, Universidad del Valle, 2002. [ Links ]
[19] SODERSTROM, TORSTEN. System Identification. Prentice Hall. 1989. [ Links ]
[20] DAVIS, W.D.T. System Identification for Self Adaptive Control. Wiley Interscience. 1970. [ Links ]
[21] LANDAU, IOAN DORE. . Identification et Commande des Systemes. Edition Hermés. 1993. [ Links ]
[22] LJUNG, L. System Identification: Theory for the User. Prentice Hall 1987. [ Links ]
[23] SMITH C AND CORRIPIO C. Principles and Practice of Automatic Process Control. John Wiley and Sons, 2 ed, 1997. [ Links ]
[24] OROZCO, MARTHA. Diseño e Implementación de un Regulador de Voltaje para un Generador Sincrónico. Tesis de Maestría en Ingeniería - Automática. Universidad del Valle. 2005. [ Links ]
[25] IEEE Committee Report. (Digital Excitation Applications Task Force of the Excitation Systems Subcommittee). Computer Models for Representation of Digital - Based Excitation Systems. IEEE Transactions on Energy Conversion, Sep 1996. [ Links ]














