Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.75 n.156 Medellín set./dez. 2008
SICOMPC: SIMULADOR PARA CONTROL PREDICTIVO BASADO EN MODELOS
SICOMPC: SIMULATOR FOR MODEL PREDICTIVE CONTROL
ROBIN SALCEDO
Ingeniero Electrónico, Universidad Industrial de Santander
RODRIGO CORREA
Ingeniero Químico, Ph.D, profesor titular, Universidad Industrial de Santander crcorrea@uis.edu.co
Recibido para revisar Octubre 12 de 2007, aceptado Enero 21 de 2008, versión final Febrero 11 de 2008
RESUMEN: En este artículo se describe la herramienta computacional SICOMPC desarrollada con el fin de poder disponer de un programa para simulación de control predictivo basado en modelos. Si bien existen en el mercado algunos programas dedicados al control predictivo, ellos son en su mayoría costosos y de estructura cerrada. SICOMPC de otro lado tiene una estructura modular e incluye además ventanas donde se puede simular las estrategias clásicas de control, con el fin de compararlas bajo criterios de estabilidad y robustez en diversos modelos de plantas de procesos.
PALABRAS CLAVE: Control Predictivo, Matriz Dinámica de Control (DMC), Control Predictivo Basado en Modelos de Espacio de Estados (SSMPC), Control PID.
ABSTRACT: This article describes the software SICOMPC created for the simulation of a predictive control system. A model predictive control (MPC) and a dynamic matrix control (DMC) were the predictive control strategy used in this software. The ideal PID compensator was also implemented for comparison purpose. Stability and robustness were the comparison criteria.
KEY WORDS: Predictive control, dynamic matrix control, predictive control based on models, pid controller.
1. INTRODUCCIÓN
El control predictivo tiene como objetivo resolver problemas de control y automatización de procesos industriales, que presentan un comportamiento dinámico difícil, inestables, de fase no-mínima y sistemas con retardos y perturbaciones [1]. El control predictivo basado en modelos (MPC) se puede interpretar como una estrategia de control que utiliza de forma explícita un modelo matemático interno del proceso a controlar (modelo de predicción). Este modelo se utiliza para predecir la evolución de las variables a controlar a lo largo de un horizonte temporal de predicción; de este modo
se pueden calcular las variables manipuladas futuras para lograr que en El horizonte de predicción, las variables controladas converjan a los valores de referencia. Una de las propiedades más atractivas del MPC es su formulación abierta que permite la incorporación de distintos tipos de modelos de predicción, así como la consideración de restricciones sobre las señales del sistema [4].
2. FUNDAMENTOS
2.1 Control predictivo y control PID
A continuación de describen algunos aspectos generales sobre MPC, pero para un tratamiento profundo y completo se Remite al lector a las referencias citadas. El control MPC posee principalmente tres elementos, y para cada uno de estos se pueden elegir diversas opciones, generando distintos algoritmos. Estos elementos son el modelo de predicción, la función objetivo y la obtención de la ley de control. Las metodologías del diseño de sistemas de control actuales se basan en la formulación de modelos lineales y no lineales para reflejar el comportamiento dinámico de un proceso. La aplicación del control predictivo usando un modelo lineal permite conocer la evolución del proceso en un horizonte de predicción ante cualquier valor de la entrada; dicha evolución estará afectada de forma lineal por la influencia de acciones pasadas y futuras [2-4]. Si bien los algoritmos clásicos son aun válidos para el mantenimiento de la estabilidad en las variables de calidad en la mayoría los procesos, presentan un problema fundamental; no están preparados para responder ante determinadas evoluciones dinámicas del proceso, caracterizadas por la aparición de importantes no linealidades, retardos puros, respuestas inversas y tampoco resuelven los problemas de acoplamiento entre diversas variables. Estos problemas inherentes a su propia concepción y diseño, son la causa de la inestabilidad del sistema; este aspecto se trata mas a fondo en la referencias [4-5]. La figura 1 muestra las estrategias de control MPC y control PID.
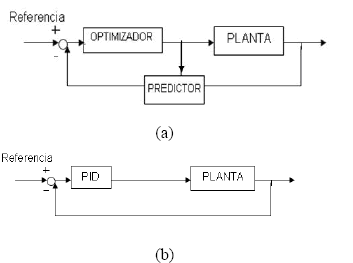
Figura 1. Diagramas de control. a. Control Predictivo. b. Control PID
Figure 1. Control diagrams. a. Predictive control b. PID control
2.2 Control predictivo basado en modelos
El Control Predictivo Basado en Modelos (MPC), constituye un campo muy amplio de métodos de control; integra diversas disciplinas como control óptimo, control estocástico, control de procesos con tiempos muertos y control con restricciones [3]. El MPC es un tipo de control de naturaleza abierta dentro del cual se han desarrollado muchas aplicaciones, encontrando gran aceptación tanto en la industria como en el ámbito académico. En la actualidad existen numerosas aplicaciones de controladores predictivos funcionando con éxito, en la industria de procesos y en el control de motores y la robótica.
2.3 Aspectos generales del MPC
El MPC permite incorporar criterios operacionales a través de la utilización de una función objetivo y restricciones para el cálculo de las acciones de control. El MPC se fundamenta en los siguientes criterios:
- Utiliza el modelo matemático del proceso para predecir la evolución futura de las variables controladas sobre un horizonte de predicción.
- La imposición de una estrategia de control para el cálculo de las variables manipuladas, optimizando una función objetivo.
- El establecimiento de una trayectoria futura conocida a priori, una trayectoria de referencia actual o una trayectoria filtrada para las variables controladas del proceso.
- La aplicación de la estrategia de horizonte de control deslizante, se aplica la primera señal de control en cada instante y se desecha el resto, luego se repiten los cálculos en cada instante de muestreo.
Uno de los inconvenientes del MPC es su elevado grado de computación numérica requerido para la solución de ciertos algoritmos. También es de cierta manera una desventaja el tener que disponerse de un modelo matemático muy cercano a la planta real. Es de notar que aún existen procesos donde no se cuenta con un modelo si quiera satisfactorio que lo describa. El grado de eficiencia de una estrategia de control como MPC es dependiente en alto grado de la diferencia entre el proceso real y el nivel de precisión utilizado en la predicción que es dependiente del modelo.
2.4 Ventajas del control MPC sobre el control convencional
El MPC desde su creación ha mantenido consistentemente varias características que lo diferencian no solo del control convencional sino de otras técnicas modernas como el control adaptativo, LQ de auto ajuste, entre otros. De ellas se destacan:[2-5]:
- Sencillo de comprender. Algunos autores atribuyen esta sencillez a su carácter intuitivo.
- Maneja tanto sistemas de una sola variable como los multivariables.
- La compensación con retardo, así como su ajuste es comparativamente muy fácil.
- Trabaja muy cercanamente a los límites reales (restricciones) impuestos a la planta, permitiendo ello maximizar rendimientos.
2.5 Forma de operación de un MPC
La metodología del control MPC se caracteriza por la siguiente secuencia de eventos:
1. Para cada tiempo t y haciendo uso del modelo del proceso se predicen las salidas futuras para un determinado horizonte de predicción 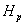 .
.
Estas salidas predichas, dependen de los valores conocidos hasta el instante t (entradas y salidas pasadas)
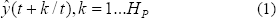
y de las señales de control futuras
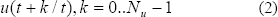
La nomenclatura general 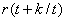 indica que el cálculo en el instante
indica que el cálculo en el instante 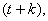 depende de su valor inmediatamente anterior en
depende de su valor inmediatamente anterior en 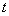 .
.
2. Las señales de control futuras se calculan empleando un criterio de optimización en el que se busca mantener el proceso lo más próximo posible a la trayectoria de referencia, que usualmente es el punto de ajuste o una trayectoria conocida. Este criterio es en ciertos casos una función cuadrática de los errores entre la salida predicha por el modelo matemático y la trayectoria de referencia predicha (similar al planteamiento del criterio de mínimos cuadrados). Para el caso en que se tenga una función, conocida en optimización como función objetivo, cuadrática, un modelo matemático lineal y si no existen restricciones (ni activas ni pasivas), se puede obtener una solución explícita de esta función. Si en cambio el problema posee por ejemplo un modelo no linealizable alrededor del punto de operación, se requiere hacer uso de un método numérico de tipo iterativo para la optimización mediante programación cuadrática.
3. Envío de únicamente la primera señal de control 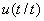 al proceso, desechándose las otras calculadas, puesto que en el siguiente instante de muestreo ya se conoce
al proceso, desechándose las otras calculadas, puesto que en el siguiente instante de muestreo ya se conoce 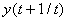 , repitiéndose nuevamente el paso 1; con este nuevo valor todas las secuencias se deben actualizar. Luego se calcula
, repitiéndose nuevamente el paso 1; con este nuevo valor todas las secuencias se deben actualizar. Luego se calcula 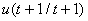 , que en principio será diferente a
, que en principio será diferente a 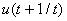 al disponer de nueva información; este procedimiento se conoce en la literatura como horizonte móvil o deslizante.
al disponer de nueva información; este procedimiento se conoce en la literatura como horizonte móvil o deslizante.
2.6 Estructura típica de un MPC
En la estructura del MPC, se usa el modelo matemático del proceso (planta) para predecir sus salidas futuras, basándose en las señales de control futuras. Estas señales se calculan con ayuda de un programa de optimización que siempre requiere del planteamiento de una función objetivo y de ser el caso, de restricciones activas o pasivas. Este modelo matemático debe ser capaz de describir en forma muy cercana la dinámica del proceso para poder predecir las salidas futuras. Otros componentes estructurales de un control MPC son la trayectoria de referencia, los errores futuros (diferencia entre la trayectoria de referencia y las salidas predichas) y las señales de control futuras. La figura 2 muestra la estructura típica de un control MPC; en ella SP son la salidas predichas, TR es la trayectoria de referencia, ERR es el error, CF son los controles futuros y E/S son las entradas salidas al modelo.
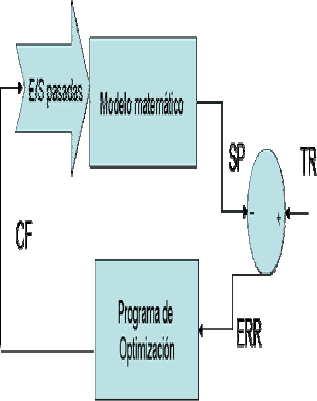
Figura 2. Estructura de control MPC
Figure 2. MPC structure
En contraste con el modelo utilizado en control convencional, esto es, un modelo nominal, en el caso de MPC se requiere de un modelo más elaborado pero con la contradicción de que entre más preciso sea, eventualmente requerirá más tiempo de cómputo punto que puede ser neurálgico en algunas aplicaciones.
3. SIMULADOR SICOMPC
3.1 Diagrama de funcionamiento de la herramienta SICOMPC
La figura 3 muestra el diagrama del funcionamiento de la herramienta.
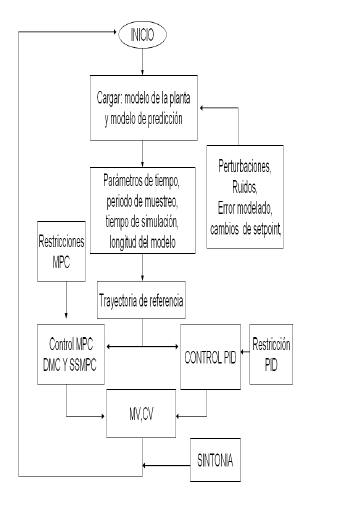
Figura 3. Diagrama de flujo del SICOMPC
Figure 3. SICOMPC Flow diagram
Como se observa la herramienta tiene una estructura modular en donde cada uno de ellos tiene una función específica; esto facilita le seguimiento de la lógica con el fin de depurar el programa.
3.2 Ventana de inicio de la Herramienta SICOMPCLa figura 4 muestra la ventana inicial de SICOMPC. En esta ventana el usuario selecciona si desea trabajar con MPC o con la representación en espacio de estados. Seguidamente completa toda la información requerida llenando los espacios apropiados. Por razones de edición resultó imposible incrementar el tamaño de la figura.
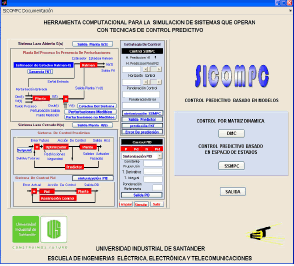
Figura 4. Ventana de inicio SICOMPC, versión en español
Figure 4. Initial window of SICOM, Spanish version
3.3 Algoritmo de control DMC
La figura 5 muestra la ventana de configuración del algoritmo de control DMC
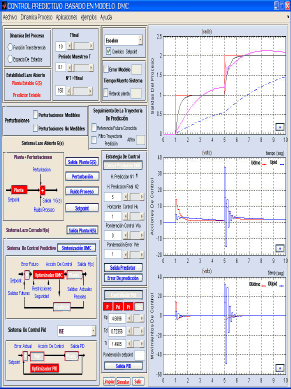
Figura 5. Ventana principal para el DMC
Figure 5. Principal window for DMC
En esta ventana se incluye toda la información pertinente al proceso a ser controlado, obteniéndose la respuesta en ella misma. Esta se puede variar directamente por el usuario facilitando de esta manera su análisis.
3.4 Algoritmo de control SSMPC
La figura 6 muestra la ventana de configuración del algoritmo de control SSMPC. Una vez se seleccionó trabajar en el espacio de estados, en esta ventana se procede a completar toda la información, seguidamente aparecen los resultados de la simulación.
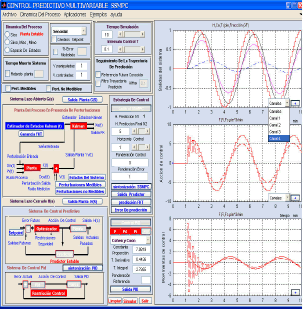
Figura 6. Ventana principal para el SSMPC
Figure 6. Principal window for SSMPC
3.5 Estrategia de control predictivo
La figura 7 muestra el diagrama de bloques del control predictivo implementado en la herramienta SICOMPC. Esta ventana permite al usuario tener presente sobre la estructura de un compensador predictivo típico.
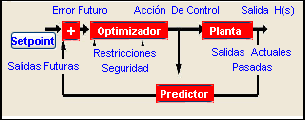
Figura 7. Estructura de control predictivo (SICOMPC)
Figure 7. Predictive control structure (SICOMPC)
La figura 8 muestra el panel donde el usuario introduce los parámetros del controlador predictivo. En caso de que sea el control SSMPC para sistemas multivariables, los parámetros de ponderación son vectores que corresponden con las dimensiones del sistema.
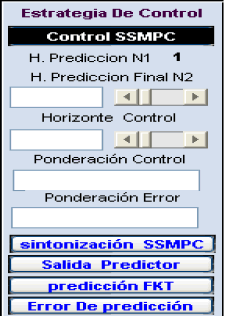
Figura 8. Parámetros del control predictivo
Figure 8. Predictive control parameters
3.7 Estrategia control PID ideal
La figura 9 muestra la estructura del controlador PID ideal.

Figura 9. Estructura del control PID
Figure 9. Structure of the PID control
Se selecciona el tipo de controlador, (P, PI, PD y PID). Se introducen los parámetros (kp, ti, td) y la ponderación de referencia.
Adicionalmente la herramienta de simulación de control predictivo basado en modelos brinda al usuario final la facilidad de modificar el escenario de control, a continuación se mencionan las opciones disponibles en SICOMPC:
- Cambios de referencia (escalón, pulso, rampa, senoidal, diente sierra, triangular tren de pulsos).
- Error de modelado de la planta del proceso
- Filtro de la trayectoria de referencia.
- Adición de perturbaciones.
- Solución sin y con restricciones de seguridad en las variables del proceso.
- Solución con estimación de estados.
La documentación del simulador SICOMPC se encuentra disponible para el usuario mediante ayudas y videos tutoriales en la aplicación.
4. PRUEBAS Y RESULTADOS
4.1 Aplicación del algoritmo de control DMC
Se tiene la siguiente función de transferencia que identifica a un proceso de control monovariable de temperatura para un intercambiador de calor.
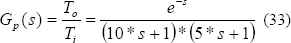
El sistema posee intrínsecamente retardos puros, se desea controlar la temperatura de salida del intercambiador de calor mediante la manipulación de la temperatura de entrada del sistema, la referencia temperatura es generada mediante un cambio de temperatura de 0ºC a 1ºC en la entrada del sistema. Se desea compensar el efecto del retardo de tal forma que el sistema se estabilice lo más rápido posible ante esta eventualidad. Se analizan la estrategia de control predictivo DMC contra la estrategia de control PID para el control de este proceso. A continuación se muestran los parámetros para el diseño de los dos controladores.
Parámetros del control DMC: 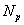 =3;
=3; 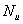 =1;
=1; 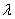 =0,
=0, 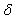 =1;
=1; 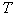 =1, N=70;
=1, N=70;
Parámetros del control PID: kp=2.27; td=1.49; ti=16.6; b=1.
La figura 10 muestra la temperatura de salida del sistema para las estrategias de control predictivo DMC y control PID. Se observa la eficiencia del control predictivo frente a sistemas con retardos, debido a que una escogencia del horizonte de predicción mucho más grande que el retardo del sistema hace que su efecto no sea considerable en la predicción. El mínimo prototipo de control, es cuando Np=td+1, siendo (td) el retardo del sistema. Para este caso el retardo del sistema es 1 y el horizonte de predicción es 3, por lo tanto en la primera iteración el control predictivo tiene conocimiento de la salida del sistema a priori, debido a esta razón cuando el sistema apenas empieza a evolucionar justo después del retardo ya el controlador predictivo tiene suficiente información para decidir adecuadamente la señal de control que enviará a la planta. La salida del control PID elimina el error en estado estable pero se ajusta la referencia de temperatura muy lentamente.
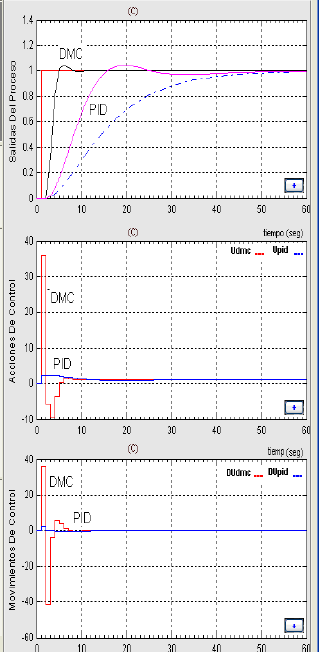
Figura 10. Temperatura de salida del horno de carbón. (Control DMC y PID)
Figure 10. Output temperature of the coal burner (DMC and PID control)
Las actuaciones de control de la temperatura de entrada son más fuertes cuando se implementa el control predictivo que con el uso de las actuaciones del PID.
4.2 Aplicación Algoritmo de control SSMPC
Control predictivo de una máquina de papel
En la figura 11 se presenta el proceso para la máquina de papel, [7]. Este ejemplo es clásico y lo desarrollan otras herramientas tales como la Toolbox de control predictivo de MATLAB. Se seleccionó dado que es muy común en la mayoría de textos clásicos en control predictivo por su fácil interpretación y manejo.
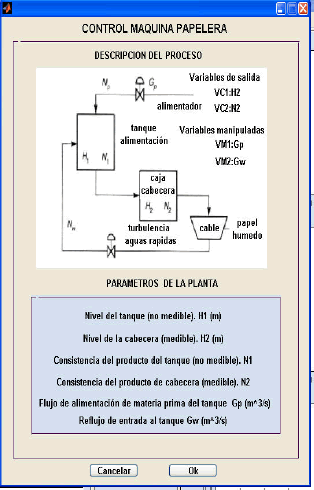
Figura 11. Planta máquina de papel
Figure 11. Paper machine with headbox
Las variables controladas del proceso son:
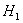 nivel del tanque,
nivel del tanque, 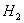 nivel de la cabecera,
nivel de la cabecera, 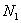 consistencia del producto del tanque,
consistencia del producto del tanque, 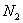 consistencia del producto de cabecera
consistencia del producto de cabecera
Las variables manipuladas del proceso son:
Gp flujo de alimentación de materia prima del tanque, Gw reflujo de entrada al tanque.
La dinámica del sistema a controlar se identifica en espacio de estados, [7]:
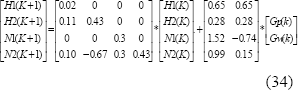
El sistema para la máquina de papel busca controlar el nivel del tanque del agua y la consistencia del tanque mediante la manipulación de los flujos de alimentación y el flujo entrante.
Parámetros del control SSMPC: 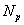 =10;
=10; 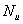 =3;
=3; 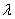 = [0.6; 0.6],
= [0.6; 0.6], 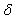 = [3.2; 3.2];
= [3.2; 3.2]; 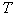 =0.1;
=0.1;
En la figura 12 se muestra la respuesta del sistema de la máquina de papel.
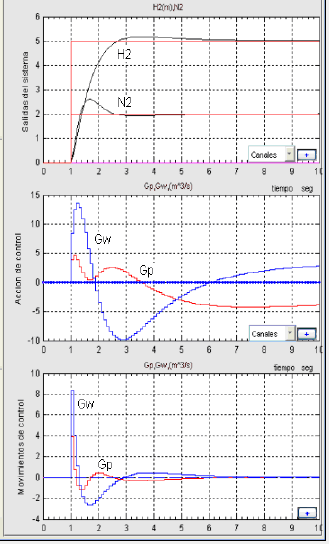
Figura 12. Control de nivel y consistencia del tanque de agua en la máquina de papel
Figure 12. Level and consistency control for a water tank in a paper machine
Como resultado el nivel de cabecera y la consistencia del producto logra estabilizarse en sus puntos de ajustes muy rápidamente, se eliminan los errores estacionarios. Las actuaciones de control son fuertes en los primeros instantes de error. Como se observa en la figura 13 las acciones de los flujos interactúan en todo el proceso para mantener las variables controladas en sus referencias. A continuación se presenta cinco segundos después de iniciado el proceso un cambio en el punto de ajuste del nivel del tanque de tal forma que disminuye de 5 a 4 metros, el punto ajustado para la consistencia del tanque se mantiene igual en todo el proceso. Se desea controlar la planta frente a esta eventualidad.
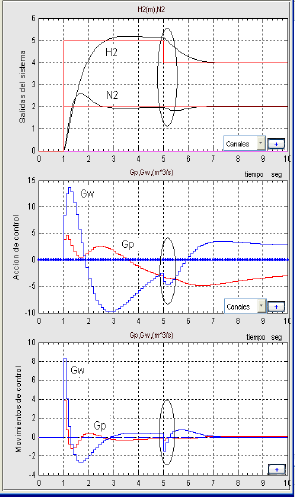
Figura 13. Control de nivel y consistencia del tanque de agua en la máquina de papel, (Cambio en el punto de ajuste)
Figure 13. Level and consistency control for a water tank in a paper machine (changes in the set-point)
Esta figura muestra como reacciona el sistema frente a un cambio en el punto de ajuste; se debe notar la interacción entre las variables debido a que cuando se afecta la referencia del nivel del tanque, la consistencia del tanque también se afecta y actúa de acuerdo a la dinámica del proceso. Lo mismo sucede para las actuaciones de las señales de flujo que interviene en la máquina de papel.
5. CONCLUSIONES
Aunque existen otros programas de simulación para el control predictivo tales como la Toolbox de control predictivo de MATLABTM, IMPACT, MIMO-GPCIT, SISO-GPCIT, se optó por desarrollar, utilizando la facilidad gráfica que posee MATLAB (GUI), una versión modular que permita crecer y que no posea las limitaciones típicas cuando se adquiere un programa comercial. Este crecimiento se facilita por ser un desarrollo propio dentro de una estructura modular, es decir, se podrá mejorar, adicionar o incluso eliminar un módulo sin que se afecte el sistema global. Al comparase con otros programas destacamos como SICOMPC, en su primera versión, realiza las mismas actividades incluyendo el manejo en el espacio de estados, se puede acondicionar para que a futuro maneje restricciones operacionales mas exigentes. El módulo de optimización se está habilitando para hacerlo mas eficiente y robusto mediante varias técnicas de búsquedas de óptimos absolutos. Esta herramienta se describe en detalle en la referencia [9].
El simulador SICOMPC para control predictivo en espacio de estados y mediante matriz dinámica de control, constituye una herramienta muy práctica para el estudio del control predictivo en las prestaciones de lazo cerrado. El usuario puede encontrar en esta aplicación un primer contacto con este tipo de controladores, previo paso al desarrollo teórico. Al mismo tiempo éste puede obtener la validación de sus propios diseños de una forma rápida y fiable. Esta herramienta computacional permite implementar las estrategias de control predictivo de una forma sencilla gracias a su interfaz gráfica; además, permite configurar estrategias de control PID convencionales con el fin de comparar criterios de rendimiento con los controladores predictivos. La herramienta computacional cumple con criterios de desempeño, y validación propias de un programa de uso especializado.
Como trabajo futuro y con el objetivo de ir expandiendo esta herramienta se incluirán otros módulos de control predictivo como GPC, MAC, QDMC, entre otras técnicas avanzadas en control predictivo existentes, al igual que programarla en visual C++ que permitan ser compiladas y utilizadas posteriormente con la interfase gráfica de MATLAB.
REFERENCIAS
[1] US Patent No. 4349869, Sep 14, 1982. [ Links ]
[2]. BEQUETTE B. WAYNE. Process Control: Modelling, Design and Simulation (Prentice-Hall International Series in the Physical and Chemi),Upper Saddle River, NJ (2003). pp. 487-519. [ Links ]
[3] BORDÓNS ALBA, CARLOS. Control Predictivo: metodología, tecnología y nuevas perspectivas, Aguadulce, Almería: Departamento de Ingeniería de Sistemas y Automática Universidad de Sevilla, 2000. 73 p. [ Links ]
[4] UREÑA TREJOS. CRISTIAN, MURILLO SOLÍ. IVÁN. Introducción al control predictivo, Universidad de Costa Rica, Escuela de Ingeniería Eléctrica, Departamento de Automática, 2003. 22p. [ Links ]
[5] ROSSITER. J. ANTHONY. Model-Based Predictive Control: A Practical Approach, CRC Press, New York, Technology & Industrial Arts, 2003. 318 p.
[6] DANIEL R. LEWIN. Lecture 12: Model Predictive Control. Process Control System Design (online), Department of Chemical Engineering, Technion, Haifa, Israel , March 14, 2005. 17 p. [ Links ]
[7] GARCÍA NIETO. S, MARTÍNEZ. SANCHOS. Resumen: Simulador de Controladores Predictivos Multivariables Con Modelos en Espacio de Estados, Dpto. de ingeniería de sistemas y automática. Universidad politécnica de valencia. 8p, 2005. [ Links ]
[8] ALFARO, VÍCTOR. Identificación de los modelos para los procesos controlados. San José de Costa Rica, Universidad de Costa Rica. Departamento de Automática, 2005. 20 p. [ Links ]
[9] SALCEDO B. ROBIN. Trabajo de grado, Escuela de Ingenierías Eléctrica, Electrónica y de Telecomunicaciones, Universidad Industrial de Santander, (2007). [ Links ]














