Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
DYNA
versión impresa ISSN 0012-7353versión On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.75 n.156 Medellín sep./dic. 2008
UNA HERRAMIENTA MATRICIAL PARA EL MODELADO EN 2-D DE ALGUNOS PROBLEMAS DE CONTACTO ELÁSTICO
A MATRIX–TOOL FOR THE 2-D MODELLING OF SOME ELASTIC CONTACT PROBLEMS
FABIO ALEXANDER SUÁREZ
Grupo de Tribología y Superficies, Universidad Nacional de Colombia, Medellín, alexsb75@yahoo.com
JUAN MANUEL VÉLEZ
Profesor Asociado, Grupo de Tribología y Superficies, Universidad Nacional de Colombia, Medellín, jmvelez@unalmed.edu.co
Recibido para revisar Octubre 04 de 2007, aceptado Agosto 13 de 2008, versión final Septiembre 02 de 2008
RESUMEN: En los contactos localizados, la búsqueda de las relaciones entre la carga, la geometría de los cuerpos, sus propiedades elásticas y la geometría de la zona de contacto, constituye un campo del conocimiento de alto impacto tecnológico. El conocimiento de estas relaciones permite entender mejor el comportamiento de los sistemas tribológicos para mejorar su diseño y desempeño. Este artículo busca dar a conocer una herramienta matricial útil para el modelado de problemas bidimiensionales de contactos elásticos. Basada en una generalización del problema de Flamant, dicha matriz constituye un vínculo entre los desplazamientos perpendiculares a la superficie que experimentan los puntos de ésta y la forma como se distribuye la carga en la zona de contacto, permitiendo encontrar una de estas variables en función de la otra. Esta es una herramienta sencilla y de gran utilidad para la solución de problemas complejos de este tipo. Para mostrar su utilidad, esta matriz fue empleada para resolver el problema del contacto elástico entre dos cilindros largos, problema inicialmente planteado por Hertz; los resultados encontrados son iguales a los obtenidos por Hertz en su solución analítica.
PALABRAS CLAVE: Tribología, Desgaste, Modelos, Hertz, Flamant, Mecánica del Contacto.
ABSTRACT: On the localized contacts, the search of the relationships among the load, the body geometries, their elastic properties and the contact zone geometry constitutes a field of knowledge with high technological impact. The knowledge of these relationships permits to have a better understanding of the tribological systems behavior for improving their design and their performance. This paper has as a goal to give for knowing a matrix-tool that is useful for the modeling of the 2-D problems of elastic contacts. Based on a generalization of Flamant´s problem, this matrix constitutes a link between the perpendicular displacements to the surface experienced by some points on this and the shape of the distribution of the load in the contact zone. This link permits to find one of these variables as a function of the other. The matrix is a very simple tool and has huge useful for the solution of complex problems of this kind. For showing its useful, the matrix was used to resolve the elastic contact problem between two long cylinders, a problem initially formulated and solved by Hertz; the found results are the same as those obtained by Hertz in his analytical solution.
KEY WORDS: Tribology, Wear, Models, Hertz, Flamant, Contact Mechanics.
1. INTRODUCCIÓN
La mecánica del contacto se constituye en una herramienta fundamental para realizar estudios en el área de la tribología y de la mecánica de sólidos debido a que la mayoría de las interacciones entre los componentes de máquinas se realizan a través de sus superficies; las otras interacciones son producto de los campos eléctricos, magnéticos o gravitatorios que puedan estar presentes. Las fuerzas que resultan de estas interacciones entre las superficies de los elementos generan esfuerzos de contacto. En muchos casos, los contactos tienen lugar en regiones muy localizadas de las superficies de los componentes de máquinas, alcanzándose elevados esfuerzos de contacto en dichos sitios y sus vecindades; el conocimiento de la ubicación y la magnitud de estos esfuerzos es necesario para realizar un buen diseño. Ejemplos típicos de estas situaciones se encuentran en los sistemas rueda-riel (transporte férreo), en el conjunto esfera-pista en los rodamientos, en conjuntos de engranajes y en los sistemas leva-seguidor de los motores a gasolina, entre otros.
El conocimiento de los esfuerzos y las deformaciones generados durante el contacto permite determinar la vida útil de los componentes de máquinas, la selección de sus materiales y de los tratamientos térmicos a efectuarles, entre otros. La necesidad de determinar las intensidades y las distribuciones de las cargas presentes en contactos localizados ha llevado a plantear ecuaciones en función de las cargas aplicadas, la geometría de los cuerpos en la zona de contacto y sus vecindades, de la geometría de las regiones de contacto y de las constantes elásticas de los materiales involucrados. Varios investigadores han trabajado en la solución de estos problemas centrando su atención en una geometría y/o una distribución de carga definidas. Algunos de los investigadores pioneros y más reconocidos son Hertz1,2,3, Boussinesq, Flamant2,3,4.
Hertz1, a partir de su trabajo con lentes, pretendió determinar si las deformaciones elásticas experimentadas por un par de lentes presionados entre sí influirían significativamente en sus patrones de las franjas de interferencia; sus observaciones experimentales y su conocimiento de la teoría de potencial electrostático, le permitieron elaborar su modelo de cálculo de esfuerzos y deformaciones para el contacto entre dos cuerpos cuyas superficies son caracterizadas por sus radios de curvatura. En su trabajo, Hertz supuso un contacto en ausencia de fricción entre las superficies de dos cuerpos sólidos perfectamente elásticos y una distribución parabólica para los desplazamientos normales experimentados por los puntos de estos sólidos que pertenecen a la zona de contacto1,2,3.
Boussinesq y Flamant2,3, estudiaron los problemas de deformaciones ocasionadas por fuerzas concentradas en un punto y a lo largo de una línea recta respectivamente. Estos investigadores, a diferencia de Hertz, abrieron caminos hacia la solución de problemas de contacto más complejos.
Las soluciones de problemas de mecánica del contacto aplicados a componentes de máquinas normalmente se basan en las expresiones derivadas por Hertz. Así, tanto los esfuerzos sub-superficiales como las capas endurecidas por tratamiento térmico son calculados con base en esas ecuaciones. Sin embargo, es importante considerar que, generalmente, estas expresiones son utilizadas como simples ecuaciones para cálculo de elementos de máquinas5 y no como una poderosa herramienta para la solución y la comprensión de problemas tribológicos cuando se aplican a escalas microscópicas y posiblemente nanométricas, como lo han hecho algunos investigadores6,7,8,9,10.
El presente trabajo pretende desarrollar un método general para la solución de problemas de contacto elástico modelables en dos dimensiones, caracterizados por un estado de deformación plana; este método está basado en el uso de una matriz cuyos coeficientes contienen la información relacionada con las contribuciones hechas por diferentes elementos de carga a los desplazamientos experimentados por algunos puntos de la superficie de los cuerpos en contacto. De manera general, en dicho método se consideran las siguientes variables: intensidad y forma de la distribución de la carga, estados de esfuerzos, desplazamientos y deformaciones de los puntos ubicados en la zona de contacto y sus vecindades. Adicionalmente, se aplica el método desarrollado para obtener una solución numérica al problema del contacto hertziano de dos cilindros largos alineados, la cual es contrastada con la solución analítica dada por Hertz.
2. DEFINICIÓN DEL PROBLEMA
Cuando dos cuerpos entran en contacto a través de sus superficies rugosas, éstas no se ajustan o se amoldan completamente la una sobre la otra, en este caso se dice que se tiene una condición de contactos no conformes o de contactos localizados. En este caso, los contactos están localizados en regiones muy pequeñas del área aparente de contacto.
La necesidad de determinar con exactitud la distribución e intensidad de los esfuerzos en la zona de contacto y sus vecindades para contactos no conformes es un problema tecnológico importante; su solución permitiría encontrar la situación más crítica a ser considerada durante el diseño de componentes de máquinas y ayudaría en la comprensión de algunos fenómenos tribológicos. Para la solución del problema se deben considerar la influencia de la geometría de los cuerpos en la zona de contacto y sus vecindades, las propiedades elásticas de sus materiales y la geometría de la zona de contacto ante la aplicación de una carga compresiva determinada. Los problemas de contacto a tratar se restringen a problemas modelables en dos dimensiones, donde el supuesto de un estado de deformación plana sea aplicable y en los cuales la naturaleza de los contactos sea elástica.
3. IDENTIFICACIÓN DE VARIABLES DE ENTRADA Y SALIDA
Como variables de entrada al modelo se tienen:
- Parámetro para definir la geometría de los cuerpos en la zona de contacto y sus vecindades. Para cuerpos cilíndricos se utiliza su radio de curvatura
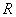 .
. - Propiedades elásticas de los materiales de los cuerpos en contacto: Módulo de Young
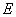 y Relación de Poisson
y Relación de Poisson 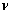 .
. - Desplazamientos normales a la superficie experimentados por puntos superficiales definidos por una función
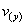 .
. - Geometría de la zona de contacto, definida por su semi-ancho
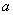 y su partición
y su partición 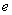 .
.
Y como variables de salida.
- Distribución de la carga en la zona de contacto definida por una función
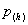 .
. - Magnitud de la carga aplicada en la zona de contacto por unidad de longitud
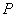 .
.
4. CONSTRUCCIÓN DEL MODELO
Para la construcción de este modelo se hace uso de una generalización del problema estudiado por Flamant2,3,4 (determinación de los esfuerzos, los desplazamientos y las deformaciones experimentados por un cuerpo elástico, isotrópico y semi-infinito, al aplicarle una carga uniformemente distribuida perpendicular a su superficie a lo largo de una línea recta) con el objetivo de aplicar sus resultados a la solución de problemas más reales de ingeniería, en los cuales las cargas aplicadas se distribuyen sobre áreas finitas de forma rectangular de tal manera que se permite alcanzar un estado de deformación plana2,3,11.
Existen problemas de contacto que resultan difíciles de visualizar desde el punto de vista analítico, ya que las distribuciones de carga deben ser representadas por complejas expresiones matemáticas; además, si se considera la presencia de deslizamientos parciales que generan tracción en las superficies producto de la fricción allí presente, el problema se tornaría más complicado.
Si la distribución de la carga aplicada en la zona de contacto es conocida, se puede determinar la distribución de esfuerzos en ésta y en sus vecindades (zona sub-superficial y/o adyacente a la superficie de contacto). La forma adoptada por la superficie del cuerpo puede ser determinada aplicando métodos analíticos o numéricos, dependiendo de la complejidad de la distribución de la carga.
Si por el contrario, se desconoce la distribución de la carga y se conocen al menos los desplazamientos verticales sufridos por algunos puntos en la superficie, ubicados dentro o fuera de la zona de contacto, es posible estimar la manera en que se distribuye la carga y luego proceder a determinar la distribución de los esfuerzos si se puede asumir el estado de deformación plana.
A continuación se muestra una manera de determinar aproximadamente la distribución de la carga de cuando se conocen los desplazamientos sufridos por N puntos ubicados en la zona de contacto y en su frontera. Para esto considérese la figura 1.
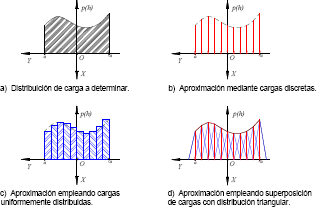
Figura 1. Aproximaciones de una distribución de carga desconocida
Figure 1. Approximations of an unknown load distribution
Supóngase que la distribución de la carga en la zona de contacto que se desea hallar tiene la forma mostrada en la figura 1a. Esta distribución puede ser representada con una buena aproximación empleando diversos elementos discretos. Varias formas de hacer esto se muestran en las figuras 1-b, c, d. Representar la carga distribuida mediante una serie de cargas discretas concentradas en diferentes puntos de la zona de contacto (figura 1b) es la forma más sencilla de hacerlo, pero tiene una gran desventaja, debido a que los desplazamientos sufridos por la superficie en los puntos donde se aplican estas cargas concentradas tienen una magnitud infinita. Al hacer una representación empleando una serie de columnas adyacentes de cargas normales uniformemente distribuidas (figura 1c) se evita este problema, pero la distribución de los desplazamientos superficiales obtenida será discontinua, es decir, los gradientes de la distribución de desplazamientos serán infinitos entre cada par elementos adyacentes. Por último, si se emplea en la representación de la carga una serie de elementos de carga normal con distribución triangular (figura 1d), es posible obtener desplazamientos superficiales que pueden ser descritos por una función suave y continua, aunque no necesariamente diferenciable.
Por lo anterior, esta última aproximación de la carga distribuida basada la superposición de elementos de carga triangulares es la que se emplea en el método que se describe a continuación.
Al considerar un elemento de carga triangular, actuando sobre la superficie plana de un cuerpo elástico (figura 2), los desplazamientos normales de los puntos superficiales estarían dados por la expresión,
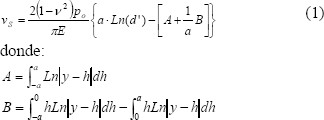
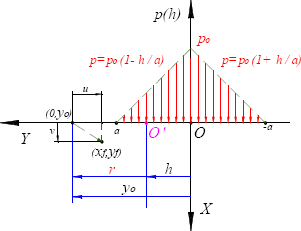
Figura 2. Carga distribuida en forma triangular (Diamante)
Figure 2. Distributed load with a triangular form (Diamond distribution)
Al analizar todos los posibles casos de interés a evaluar en estas integrales para los distintos valores de la variable 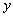 , y teniendo en cuenta que
, y teniendo en cuenta que 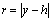 es igual a
es igual a 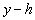 si
si 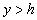 ó
ó 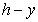 si
si 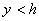 , se tiene que las variables
, se tiene que las variables 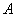 y
y 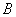 están dadas por las expresiones
están dadas por las expresiones
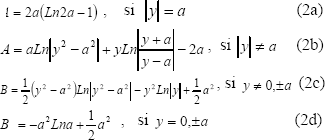
En la figura 3 se muestra la forma que adquiere la superficie debido a la acción de este elemento de carga triangular. Allí se observa que la superficie deformada en la zona de contacto tiene la forma de una V con su punta redondeada. Este comportamiento es similar al obtenido en la solución al problema de Flamant, salvo que en este último los desplazamientos sobre el eje X tienden a ser infinitos.
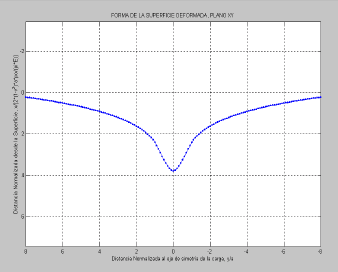
Figura 3. Superficie deformada por Carga Distribuida en Forma Triangular
Figure 3. Deformed surface by a distributed load with a triangular form
Ahora, supóngase que la carga distribuida que se desea encontrar es representada por medio de elementos de carga triangulares como se muestra en la figura 4. En ésta, la zona de contacto, de ancho 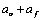 , ha sido dividida en varias sub-regiones de longitud
, ha sido dividida en varias sub-regiones de longitud 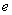 cada una; por lo tanto, se tendrán entonces
cada una; por lo tanto, se tendrán entonces 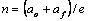 espaciados, definidos por
espaciados, definidos por 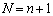 puntos nodales. Si estos puntos nodales se enumeran desde 1 en
puntos nodales. Si estos puntos nodales se enumeran desde 1 en 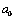 , hasta N en
, hasta N en 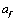 , y a cada uno de ellos se asocia un valor de carga
, y a cada uno de ellos se asocia un valor de carga 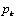 (valor máximo de carga del k-ésimo elemento de carga triangular), entonces se puede construir una matriz cuyos coeficientes cuantifican el aporte efectuando por cada uno de los elementos de carga al desplazamiento total experimentado por uno de los puntos nodales.
(valor máximo de carga del k-ésimo elemento de carga triangular), entonces se puede construir una matriz cuyos coeficientes cuantifican el aporte efectuando por cada uno de los elementos de carga al desplazamiento total experimentado por uno de los puntos nodales.
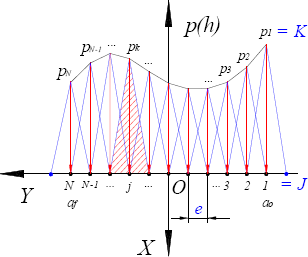
Figura 4. Aproximación de la distribución de carga por medio de elementos de carga triangulares
Figure 4. Approximation of the load distribution by triangular load elements
Para construir la matriz, solo es necesario hacer una generalización del resultado obtenido en la Ec-1 y así determinar los desplazamientos normales de los puntos de la superficie, generados por el conjunto de los 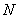 elementos de carga triangular. En esta matriz, denominada matriz
elementos de carga triangular. En esta matriz, denominada matriz 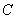 , cada una de sus componentes
, cada una de sus componentes 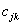 representa la contribución del k-ésimo elemento de carga al desplazamiento sufrido por el j-ésimo punto nodal. De esta manera, en notación matricial, el desplazamiento total sufrido por el j-ésimo punto nodal se puede escribir como
representa la contribución del k-ésimo elemento de carga al desplazamiento sufrido por el j-ésimo punto nodal. De esta manera, en notación matricial, el desplazamiento total sufrido por el j-ésimo punto nodal se puede escribir como
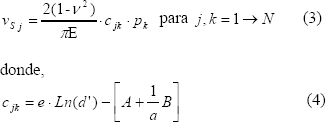
Resultado obtenido al sustituir en la Ec-1 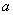 por
por 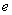 . Haciendo esta misma consideración y empleando las expresiones de la Ec-2, se determinan los valores de las variables A y B asociados a cada
. Haciendo esta misma consideración y empleando las expresiones de la Ec-2, se determinan los valores de las variables A y B asociados a cada 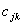 .
.
Como puede observase, los coeficientes de la matriz C cuantifican el efecto en el desplazamiento de cada punto nodal debido a un elemento de carga unitario ubicado a una cierta distancia 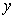 de dicho punto; siendo ésta su interpretación física asociada al problema de estudio.
de dicho punto; siendo ésta su interpretación física asociada al problema de estudio.
Los vectores 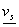 y
y 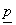 representan respectivamente los desplazamientos de los
representan respectivamente los desplazamientos de los 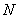 puntos nodales y las cargas máximas asociadas a cada elemento de carga triangular. De la Ec.-3 se observa que, si se conocen los desplazamientos totales
puntos nodales y las cargas máximas asociadas a cada elemento de carga triangular. De la Ec.-3 se observa que, si se conocen los desplazamientos totales 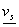 experimentados por los
experimentados por los 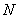 puntos nodales y se halla la matriz de coeficientes
puntos nodales y se halla la matriz de coeficientes 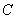 , es posible encontrar los valores de los coeficientes de carga máxima de cada elemento, coeficientes del vector
, es posible encontrar los valores de los coeficientes de carga máxima de cada elemento, coeficientes del vector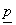 , de la siguiente manera:
, de la siguiente manera:
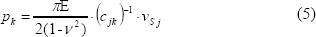
donde 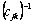 es la matriz inversa de
es la matriz inversa de 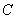 .
.
En el caso en el cual la distribución de carga sea conocida y se desee determinar la forma de la superficie deformada en la zona de contacto (e incluso en sus alrededores, aunque para esto se deben hacer unas pequeñas reformas o recurrir a algunos artificios matemáticos), basta con efectuar el producto matricial indicado por la Ec-3 y se encuentran así los desplazamientos de los puntos clave de una forma rápida y sencilla sin importar mucho la complejidad de la distribución de la carga.
Para determinar la contribución de un elemento de carga en particular sobre un nodo específico (figura 5), primero hay que averiguar si este nodo coincide con el nodo asociado a este elemento (Punto nodal tipo 1), si hace parte de la frontera del elemento de carga (Punto nodal tipo 2) o si simplemente es un punto exterior a dicho elemento (Punto nodal tipo 3). Luego, se procede a emplear la expresión adecuada para hallar la contribución. Esta expresión se obtiene de las encontradas de manera analítica para el caso mostrado para un elemento de carga triangular, las cuales se resumen en la Ec- 2.
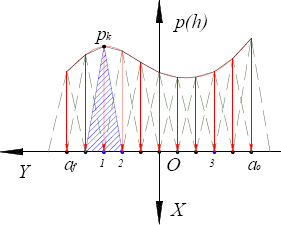
Figura 5. Tipos de puntos nodales según su ubicación respecto a un elemento de carga
Figure 5. Types of key points according to their position with regard to one load element
El elemento de carga triangular (figuras 2 y 4) es un elemento sencillo cuyas contribuciones a los desplazamientos han sido ya estudiadas3,4,11. La unión de dos mitades de estos elementos consecutivos permite realizar una aproximación lineal del tramo de la distribución de carga ubicado entre estos como se muestra en la figura 6 (es como si se emplearan trapecios como elementos de carga para representar la carga distribuida, siendo más sencillo trabajar con elementos triangulares)11.
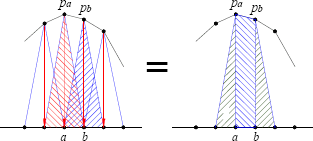
Figura 6. El elemento de carga triangular y su relación con un elemento trapezoidal
Figure 6. A triangular load element and its relation with a trapezoid element
Al aproximar distribuciones de carga que no sean nulas en su frontera, tal y como se ha mostrado en la figura 1a, se observa que en ésta, una parte de los elementos empleados quedan fuera de la zona de contacto (pueden también quedar ubicados dentro de la zona de contacto), lo cual introduce un error al estimar la distribución de carga o los desplazamientos según sea el caso. Sin embargo, debe tenerse en cuenta que lo mostrado con respecto a esto en las figuras 1d y 4 es una situación exagerada de lo que realmente se presenta cuando se emplea el método antes descrito. Gracias a la posibilidad que ofrecen los computadores de hacer muchas operaciones en poco tiempo, el tamaño del espaciado 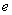 puede escogerse lo suficientemente pequeño, para que los elementos así generados se ajusten bastante bien a la forma de las cargas con estas características en su frontera.
puede escogerse lo suficientemente pequeño, para que los elementos así generados se ajusten bastante bien a la forma de las cargas con estas características en su frontera.
Una gran ventaja de este método reside en el hecho que la matriz 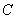 es una constante para un valor de
es una constante para un valor de 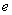 específico, y por lo tanto, si se construye una buena matriz (
específico, y por lo tanto, si se construye una buena matriz (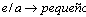 ), ésta puede guardarse y emplearse para diferentes problemas de estudio. De esta manera se reduce todo a obtener bien sea el vector de distribución de la carga
), ésta puede guardarse y emplearse para diferentes problemas de estudio. De esta manera se reduce todo a obtener bien sea el vector de distribución de la carga 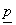 o el vector de desplazamientos superficiales normales
o el vector de desplazamientos superficiales normales 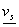 , y determinar a partir de estos, el vector incógnita en cada caso empleando la Ec- 3 ó la Ec-5.
, y determinar a partir de estos, el vector incógnita en cada caso empleando la Ec- 3 ó la Ec-5.
La figura 7 muestra una representación gráfica de una matriz 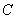 , construida empleando una relación
, construida empleando una relación 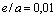 . La matriz
. La matriz 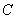 posee una alta simetría y esto permite también ahorrar muchos cómputos operacionales a la hora de calcular sus coeficientes. Como puede deducirse de la figura 7, basta sólo determinar prácticamente la cuarta parte de sus coeficientes para tener la matriz completa.
posee una alta simetría y esto permite también ahorrar muchos cómputos operacionales a la hora de calcular sus coeficientes. Como puede deducirse de la figura 7, basta sólo determinar prácticamente la cuarta parte de sus coeficientes para tener la matriz completa.
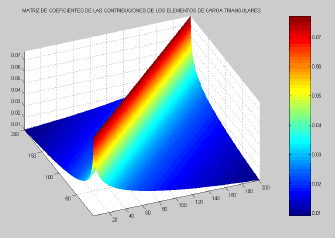
Figura 7. Gráfica de la matriz de coeficientes C para -ao= af =a = 1, e/a = 0.01
Figure 7. Graphic of the Coefficient Matrix C for a =-ao= af = 1, , e/a = 0.01
5. APLICACIÓN DEL MÉTODO EN SOLUCIÓN DE UN PROBLEMA DE UN CONTACTO HERTZIANO
Con base en el procedimiento descrito a partir de la generalización del problema de Flamant y con el uso de la matriz de coeficientes se encontrará la solución de uno de los problemas estudiados por Hertz, el problema del contacto entre dos cilindros largos y alineados cuyos radios y propiedades elásticas son conocidas. Adicionalmente, esto permitirá probar la aplicabilidad del método desarrollado al contrastar la solución numérica obtenida con la solución analítica dada por Hertz.
Un cuerpo de material isotrópico perfectamente elástico, con forma cilíndrica, bastante largo y cuya geometría se halla caracterizada por su radio de curvatura 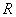 , es puesto en contacto inicialmente bajo la acción de una carga normal nula contra la superficie plana de otro cuerpo que es totalmente rígido (figura 8a). En este caso, el contacto tiene lugar a lo largo de una línea recta. Si se incrementa la carga intentando unir este cuerpo a la superficie, el cilindro se deformará, convirtiéndose la zona de contacto en una región rectangular de semiancho
, es puesto en contacto inicialmente bajo la acción de una carga normal nula contra la superficie plana de otro cuerpo que es totalmente rígido (figura 8a). En este caso, el contacto tiene lugar a lo largo de una línea recta. Si se incrementa la carga intentando unir este cuerpo a la superficie, el cilindro se deformará, convirtiéndose la zona de contacto en una región rectangular de semiancho 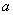 unidades de longitud (figura 8b).
unidades de longitud (figura 8b).
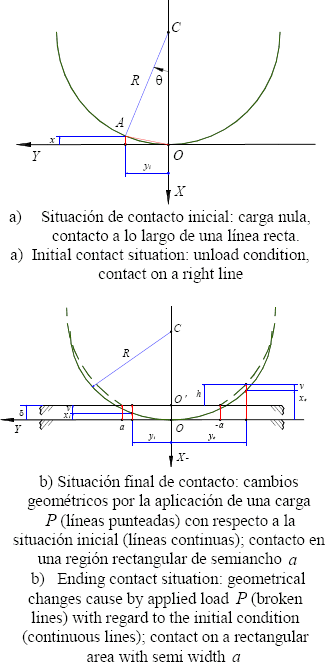
Figura 8. Contacto entre un cilindro deformable y una superficie plana rígida
Figure 8. Contact between a deformable cylinder and a rigid plain surface
Supóngase que en este estado, la carga aplicada por unidad de longitud 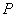 , es igual o inferior al valor crítico necesario para que se genere un flujo plástico y los cuerpos se hallan en una condición de equilibrio estático. Debido a que el cuerpo deformable es lo suficientemente largo, es posible alcanzar un estado de deformación plana. Suponiendo que
, es igual o inferior al valor crítico necesario para que se genere un flujo plástico y los cuerpos se hallan en una condición de equilibrio estático. Debido a que el cuerpo deformable es lo suficientemente largo, es posible alcanzar un estado de deformación plana. Suponiendo que 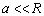 y despreciando los efectos de la fricción debidos a los micro-deslizamientos que tienen lugar durante el tiempo de carga y más aún, despreciando los micro-desplazamientos que ocurren en la dirección tangente a las superficies (es decir los puntos en contacto sólo se desplazan en dirección perpendicular a la superficie plana), se puede elaborar un modelo sencillo y acorde con la situación real objeto de estudio, considerando las siguientes variables (figura 8):
y despreciando los efectos de la fricción debidos a los micro-deslizamientos que tienen lugar durante el tiempo de carga y más aún, despreciando los micro-desplazamientos que ocurren en la dirección tangente a las superficies (es decir los puntos en contacto sólo se desplazan en dirección perpendicular a la superficie plana), se puede elaborar un modelo sencillo y acorde con la situación real objeto de estudio, considerando las siguientes variables (figura 8):
x : Vacío o distancia inicial entre puntos correspondientes de la superficie del cuerpo deformable y la superficie plana, ubicados a una distancia y del eje X . Los subíndices i y e indican si el punto de la superficie cilíndrica se halla dentro o fuera de la zona de contacto respectivamente.
v : Desplazamiento experimentado por un punto de la superficie del cuerpo deformable desde la situación de cero carga hasta que alcanza su equilibrio estático una vez se ha aplicado la carga.
: Desplazamiento de aproximación de la superficie plana hacia el centro de curvatura del cuerpo deformable C.
h : Vacío o distancia final entre puntos correspondientes de la superficie del cuerpo deformable y la superficie plana ubicados a una distancia y del eje X .
En ausencia de carga normal, al aplicar la ley de cosenos al triángulo isósceles ACO mostrado la figura 8a, se obtiene la siguiente expresión
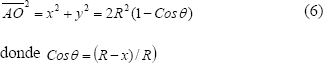
donde 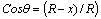
Al simplificar esta expresión se tiene que
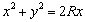
donde 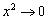 dado que x es muy pequeño; por lo tanto, al despejar
dado que x es muy pequeño; por lo tanto, al despejar 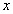 se tiene que
se tiene que

Este resultado muestra que en la zona de contacto y sus vecindades, es posible aproximar el perfil de la superficie circular del cilindro a un perfil parabólico sin cometer un error grave, permitiendo esto simplificar bastante el tratamiento matemático.
Al aplicar la carga compresiva por unidad de longitud 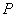 , el centro del cilindro C se acerca a la superficie plana una distancia
, el centro del cilindro C se acerca a la superficie plana una distancia 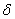 y los puntos de la zona de contacto
y los puntos de la zona de contacto 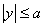 , se desplazan y entran en contacto con los puntos de la superficie plana ubicados sobre una banda de ancho
, se desplazan y entran en contacto con los puntos de la superficie plana ubicados sobre una banda de ancho 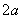 ( figura 8b). Para estos puntos se tiene que sus desplazamientos verticales v se relacionan con sus posiciones iniciales y el desplazamiento del centro C de la siguiente manera
( figura 8b). Para estos puntos se tiene que sus desplazamientos verticales v se relacionan con sus posiciones iniciales y el desplazamiento del centro C de la siguiente manera
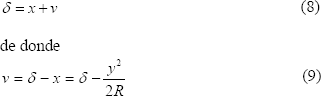
Para aquellos puntos de la superficie cercanos a la zona de contacto, 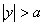 , las relaciones anteriores se transforman en
, las relaciones anteriores se transforman en
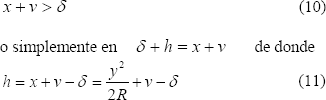
A partir de las expresiones encontradas para el sistema cilindro – superficie plana, se pueden deducir expresiones más generales que se apliquen al caso de dos cilindros deformables de radios R1 y R2 que se encuentren alineados y sean puestos en contacto.
Al utilizar la Ec-7 y aplicarla a cada superficie cilíndrica, la Ec-9, que da cuenta de los desplazamientos de los puntos superficiales al interior de la zona de contacto, se transforma en
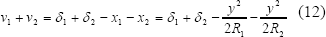
pudiéndose simplificar de la siguiente forma

al definir el acercamiento total entre los centros de los cilindros como

e introducir concepto de radio reducido del sistema,

Procediendo de manera similar, en las afueras de la zona de contacto, la Ec-10 que da cuenta de los desplazamientos de los puntos superficiales en estas regiones, se transforma en

y por lo tanto, el espacio vacío que queda en las afueras de la zona de contacto cuando se ha aplicado la carga se puede describir con la expresión
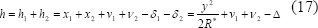
De la Ec-13 se puede observar que cuando los dos cilindros se hallan en contacto bajo la acción de una carga 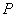 , la suma de los desplazamientos experimentados por puntos de la superficie correspondientes entre sí, que pertenecen a la zona de contacto, tiene una forma parabólica, al igual que las contribuciones de hechas por cada uno de los cuerpos. Por lo tanto, para conocer la distribución de esfuerzos generados en la zona de contacto y sus alrededores, es necesario determinar primero la distribución de la carga aplicada en la zona de contacto, de tal manera que satisfaga la condición impuesta por los desplazamientos de los puntos que entran en contacto y sus vecinos.
, la suma de los desplazamientos experimentados por puntos de la superficie correspondientes entre sí, que pertenecen a la zona de contacto, tiene una forma parabólica, al igual que las contribuciones de hechas por cada uno de los cuerpos. Por lo tanto, para conocer la distribución de esfuerzos generados en la zona de contacto y sus alrededores, es necesario determinar primero la distribución de la carga aplicada en la zona de contacto, de tal manera que satisfaga la condición impuesta por los desplazamientos de los puntos que entran en contacto y sus vecinos.
Determinación de la carga normal distribuida en la zona de contacto:
Dada la simetría del problema, los desplazamientos normales a la superficie y la distribución de carga exhiben un comportamiento simétrico con respecto al plano que contiene el eje X. Para determinar la distribución de la carga en la zona de contacto es preciso definir claramente las condiciones de frontera; para este caso, el valor alcanzado por la presión en la frontera es nulo, es decir, en 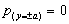 .
.
Si 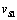 y
y 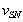 son los desplazamientos normales a la superficie experimentados por los puntos de la frontera de la zona de contacto,
son los desplazamientos normales a la superficie experimentados por los puntos de la frontera de la zona de contacto, 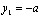 y
y 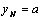 , entonces, por la simetría del problema sus valores son iguales
, entonces, por la simetría del problema sus valores son iguales 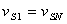 y al hacer uso de la Ec-13 se tiene que
y al hacer uso de la Ec-13 se tiene que 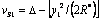 de donde
de donde 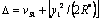 , y por lo tanto, esta expresión se puede reescribir así:
, y por lo tanto, esta expresión se puede reescribir así:
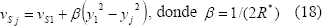
Al introducir el módulo reducido del sistema de estudio 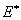 , la Ec-3 se puede modificar así
, la Ec-3 se puede modificar así
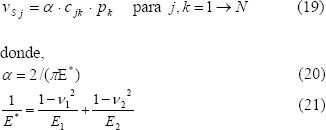
Igualando Ec-18 y 19 se obtiene una nueva expresión,
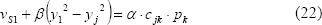
que hace referencia a un sistema de ecuaciones lineales. Ésta, al escribirse en su forma expandida para reorganizar sus términos convenientemente, se transforma un sistema equivalente de la forma
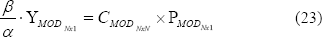
en el cual, la matriz 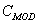 es invertible y por lo tanto, es factible hallar un único vector
es invertible y por lo tanto, es factible hallar un único vector 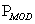 para un vector
para un vector 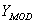 conocido,
conocido,
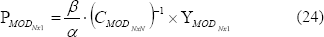
Al construir este nuevo sistema de ecuaciones lineales y resolverlo para un valor de 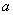 en particular, se obtienen los valores de las variables de interés en el vector
en particular, se obtienen los valores de las variables de interés en el vector 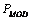 . Hecho esto y separando convenientemente sus componentes, se determina el vector que representa las cargas
. Hecho esto y separando convenientemente sus componentes, se determina el vector que representa las cargas 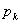 , y el vector de los desplazamientos de los puntos superficiales
, y el vector de los desplazamientos de los puntos superficiales 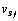 .
.
La figura 9 muestra una gráfica con los resultados encontrados para 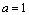 y
y 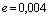 . Con base en los valores numéricos obtenidos se tiene que:
. Con base en los valores numéricos obtenidos se tiene que:
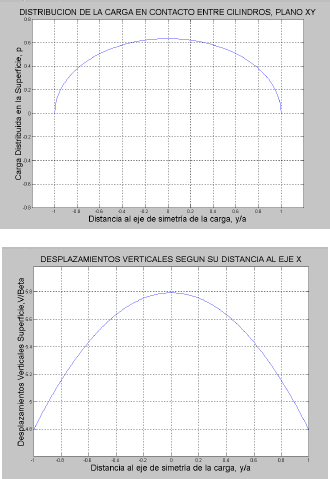
Figura 9. Distribución de la Carga y Desplazamientos en la Zona de Contacto. Parámetros empleados: a=1; e=0.0040; N=501
Figure 9. Distribution of the load and the displacements in the contact zone. Used parameters: a=1; e=0.0040;N =501
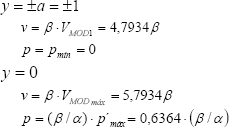
Pudiéndose mostrar fácilmente que en cada caso las componentes respectivas de los vectores 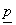 y
y 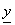 se relacionan mediante la función elíptica,
se relacionan mediante la función elíptica,
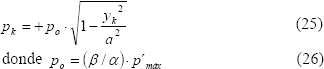
quedando así resuelto el problema de interés, al determinar la distribución de la carga en la zona de contacto para el caso de dos cilindros presionados entre sí.
Adicionalmente, con base en los resultados encontrados al variar el parámetro 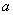 desde 0,5 hasta 4, se obtuvo que
desde 0,5 hasta 4, se obtuvo que 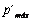 es proporcional al semi-ancho de la zona de contacto,
es proporcional al semi-ancho de la zona de contacto,
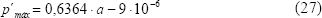
Despreciando el último término de esta expresión y sustituyendola en la Ec-26 se tiene que,
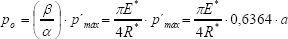
dado que para una distribución semi-elíptica, la carga total aplicada por unidad de longitud se puede expresar como
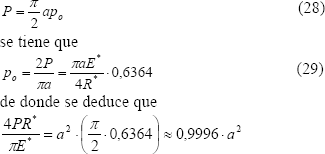
de donde se deduce que
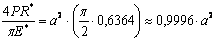
resultado que puede aproximarse a
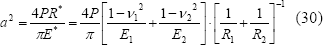
Relación que concuerda exactamente con el resultado hallado por Hertz en su trabajo. Ahora bien, en esta expresión puede verse la relación de los cuatro elementos que inicialmente se querían conjugar: geometría de los cuerpos en las vecindades de la zona de contacto (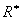 ), geometría del contacto (
), geometría del contacto (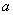 ), propiedades elásticas de los materiales (
), propiedades elásticas de los materiales (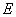 y
y 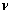 ) y carga por unidad de longitud impuesta al sistema (
) y carga por unidad de longitud impuesta al sistema (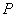 ).
).
Se debe tener en cuenta que para el caso en el cual, las superficies sean cóncavas, su radio sería negativo; y si éstas son planas, entonces su radio sería infinito.
Conocida la distribución de la carga en la zoda de contacto, basta utilizar las expresiones asociadas al problema de una carga normal distribuida para determinar las distribuciones de esfuerzos en sus vecindades11. La figura 10 muestra la distribución de esfuerzos de von Mises sobre el plano XY y sus respectivas curvas de nivel. El esfuerzo máximo tiene una magnitud de 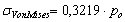 y se alcanza en la posición
y se alcanza en la posición 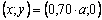 . Si se usa el criterio de flujo de Tresca, el esfuerzo máximo obtenido, con los parámetros de discretización utilizados, tiene una magnitud de
. Si se usa el criterio de flujo de Tresca, el esfuerzo máximo obtenido, con los parámetros de discretización utilizados, tiene una magnitud de 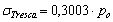 y alcanza en la posición
y alcanza en la posición 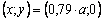 . Para este último caso, el resultado de la ubicación del punto de máximo esfuerzo difiere un poco con el valor teórico,
. Para este último caso, el resultado de la ubicación del punto de máximo esfuerzo difiere un poco con el valor teórico, 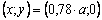 ; sin embargo el resultado obtenido es muy bueno y puede mejorarse disminuyendo el tamaño de los parámetros de discretización usados resolver las integrales asociadas al problema.
; sin embargo el resultado obtenido es muy bueno y puede mejorarse disminuyendo el tamaño de los parámetros de discretización usados resolver las integrales asociadas al problema.
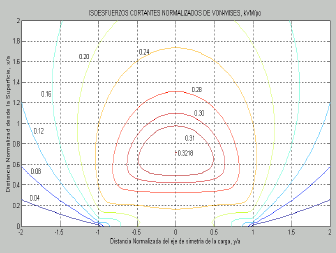
Figura 10. Esfuerzos de von Mises sobre el plano XY y sus curvas de nivel
Figure 10. Mises´s stress on the plane XY and y its level curves
Según el criterio de von Mises, la carga crítica a partir de la cual se iniciaría el flujo plástico está dada por la siguiente relación:
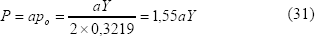
CONCLUSIONES
El método descrito para determinar los desplazamientos o la distribución de las cargas en la zona de contacto con base en el empleo de la matriz de coeficientes 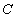 , resulta ser un método confiable y de fácil uso para abordar problemas más complejos siempre y cuando permitan ser tratados en dos dimensiones y sea aplicable el supuesto de un estado de deformación plana.
, resulta ser un método confiable y de fácil uso para abordar problemas más complejos siempre y cuando permitan ser tratados en dos dimensiones y sea aplicable el supuesto de un estado de deformación plana.
La matriz 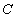 puede emplearse también para calcular desplazamientos perpendiculares a las superficies de puntos ubicados fuera de la zona de contacto. Con ella también se pueden simular problemas más complejos como por ejemplo algunos en los que se combinen varias zonas de contacto espaciadas entre sí por zonas donde las cargas aplicadas sean nulas.
puede emplearse también para calcular desplazamientos perpendiculares a las superficies de puntos ubicados fuera de la zona de contacto. Con ella también se pueden simular problemas más complejos como por ejemplo algunos en los que se combinen varias zonas de contacto espaciadas entre sí por zonas donde las cargas aplicadas sean nulas.
El método descrito puede ser complementado de tal manera que sea posible tratar problemas donde el efecto de la fuerza de fricción comience a ser relevante. Sin embargo, en la forma como se ha presentado este método, puede emplearse como una buena aproximación en aquellos casos donde el coeficiente de fricción sea bajo, es decir, inferior a 0,2 3,11,12.
REFERENCIAS
[1] HERTZ, H . On the contact of rigid elastic solids and on hardness. En: Verhandlungen des Vercins zur Beforderung des Gewerbefleisses, November 1882 , p 163-183. [ Links ]
[2] TIMOSHENCO, S., GOODIER, J.N. Theory of Elasticity. McGraw Hill Book Company, Inc. Second Edition, 1951, pp 85-96, 372-384. [ Links ]
[3] JOHNSON, K.L. Contac mechanics. Cambridge University Press 1985, 421 p. [ Links ]
[4] WILLIAMS, J. Engineering Tribology. Oxford University Press, Amen House, London, 1994. [ Links ]
[5] SHIGLEY, J.E., MISCHKE, C.R. Diseño en Ingeniería Mecánica. Editorial McGraw-Hill, Quinta Edición 1990, pp: 542-591 [ Links ]
[6] BOWDEN, F.P., TABOR, D. The friction and lubrication of solids. Oxford 1950, pp 5-57,87-105. [ Links ]
[7] ARCHARD, J.F. Contac and Rubbing of Flat Surfaces. En: Journal of applied phisycs. Vol 24, Number 8, August, 1953, p 981-988. [ Links ]
[8] GREENWOOD, J.A., WILLIAMSON, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. London, Ser. A, 295 (1966), pp 300-319. [ Links ]
[9] JOHNSON, K.L., GREENWOOD, J. A. An Adhesion Map for the Contact of Elastic Spheres. Journal of Colloid and Interface Science 192, 326–333 ,1997. [ Links ]
[10] JOHNSON, K.L. Mechanics of adhesion. Tribology International Vol. 31, No. 8, pp. 413–418, 1998. [ Links ]
[11] SUAREZ, F. Alexander. Análisis del Modelo de Archard para desgaste por deslizamiento en seco. Tesis, Universidad Nacional de Colombia, Facultad de Minas. Medellín 2002, 226p. [ Links ]
[12] HSU, S.M. SHEN M.C. RUFF, A.W. Wear prediction for metals. En: Tribology International Vol. 30 Number 5 1997 p 377-383. [ Links ]














