Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.75 n.156 Medellín set./dez. 2008
TECNOLOGIA A FIBRA OPTICA: UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLIN, UN REFERENTE LATINOAMERICANO
FIBER OPTIC TECHNOLOGY: NATIONAL UNIVERSITY OF COLOMBIA MEDELLIN CAMPUS, A LATINOAMERICAN REFERENT
RODRIGO ACUÑA
Escuela de Física, Universidad Nacional de Colombia, Medellín, racuna@unal.edu.co
JORGE GÓMEZ
Escuela de Física, Universidad Nacional de Colombia, Medellín, jagomez3@unalmed.edu.co
VICTOR ARISTIZABAL
Escuela de Física, Universidad Nacional de Colombia, Medellín, vharisti@unal.edu.co
PEDRO TORRES
Escuela de Física, Universidad Nacional de Colombia, Medellín, pitorres@unal.edu.co
Recibido para revisar Agosto 03 de 2007, aceptado Enero 28 de 2008, versión final Febrero 04 de 2008
RESUMEN: En este artículo se muestran algunos resultados de las investigaciones realizadas por el grupo de Fotónica y Opto-electrónica de la Universidad Nacional de Colombia, Sede Medellín. Se hace una breve reseña de la creación del grupo y se describen las principales aplicaciones desarrolladas, las cuales convierten al grupo en un referente Latinoamericano en el área. Se ilustran aplicaciones de las redes de Bragg en fibra óptica en sensores, simulaciones computacionales de guías de onda ópticas y la construcción de fuentes de luz láser a fibra óptica.
PALABRAS CLAVE: Fibra óptica, redes de Bragg, simulación, láser a fibra óptica.
ABSTRACT: In this paper some results concerning to researches completed by the Photonics and Opto-electronics Group of the National University of Colombia, Medellín campus, are shown. Firstly, a brief account of the creation of the group and the main applications in fiber optic technology are given, which situate to the Group as one of the most reputable Universitary group in Latin-American. Applications of fiber Bragg gratings sensor technology, computational simulation of optical waveguide, and fiber laser are shown.
KEYWORDS: Fiber optics, fiber Bragg grating, computational simulation, fiber optic laser.
1. INRODUCCION
El grupo de Fotónica y Opto-Electrónica de la Universidad Nacional de Colombia- Medellín fue creado en el año 2000 como consecuencia del estudio sobre la pertinencia de desarrollar una línea de investigación, desarrollo en innovación en sistemas a fibra óptica en Colombia. En sus inicios el grupo se concentró en el desarrollo de sistemas sensores basados en FBGs (Redes de Bragg en Fibra) debido a la Cooperación internacional con el laboratorio de sensores a fibra óptica de la Pontificia Universidade Catolica do Rio de Janeiro- Brasil; de esta forma fue posible explorar diferentes aplicaciones en sensores a fibra óptica, al igual que diferentes técnicas de medición. Posteriormente el grupo incursionó en el desarrollo de herramientas de simulación computacional que permitieron el estudio de la forma en que se guía la luz en fibras especiales y guías de onda en general. Desde el año 2005 se viene trabajando en la construcción de fuentes de luz sintonizables basadas en fibras dopadas con iones de tierras raras con el ánimo de construir sistemas de multiplexación de sensores. El grupo está formado por Profesores y estudiantes asociados a la Escuela de Física con títulos de Ph.D y M.Sc. y cuenta con convenios de cooperación con instituciones de Ciencia y Tecnología Brasileras y con ACREO-Suecia. El objetivo de este trabajo es entonces mostrar algunos de los resultados de los trabajos desarrollados por el grupo, que lo convierten en un grupo de vanguardia en Latinoamérica.
2. APLICACIONES DE FBGs
2.1 Generalidades
Una FBG es una fibra óptica en la cual el índice de refracción en cierta región del núcleo ha sido perturbado formando una modulación periódica o cuasi-periódica. Si luz con cierto espectro incide en la FBG parte del espectro es reflejado, y la máxima reflexión es dada en la llamada Longitud de Onda de Bragg, esto es;
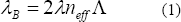
donde 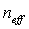 es el índice efectivo y
es el índice efectivo y 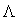 la periodicidad de la variación del índice del núcleo. Como se puede observar de la ecuación anterior, la longitud de onda de Bragg depende del índice de refracción efectivo y la periodicidad de la red, los cuales pueden ser afectados externamente por alteraciones mecánicas y térmicas del medio que la rodea; por lo tanto es posible cuantificar estas alteraciones con el simple hecho de medir los cambios en
la periodicidad de la variación del índice del núcleo. Como se puede observar de la ecuación anterior, la longitud de onda de Bragg depende del índice de refracción efectivo y la periodicidad de la red, los cuales pueden ser afectados externamente por alteraciones mecánicas y térmicas del medio que la rodea; por lo tanto es posible cuantificar estas alteraciones con el simple hecho de medir los cambios en 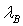 debido a las variaciones en
debido a las variaciones en 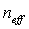 ,
, 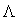 ó en ambas.
ó en ambas.
2.2 Sensor de Campo Magnético
En condiciones isotérmicas es posible demostrar que el corrimiento espectral de la longitud de onda de Bragg, según la ecuación (1) está dada por [1]:
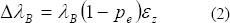
donde 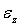 es la deformación de red y
es la deformación de red y 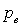 es el coeficiente elasto-óptico efectivo para deformaciones mecánicas longitudinales. Si utilizamos un material magnetoestrictivo como el terfenol, el cual responde a cambios lineales de deformación con el cuadrado del campo magnético en la dirección de este [2], para pequeñas intensidades de campo será posible escribir la ecuación (2) como [3,4,5]:
es el coeficiente elasto-óptico efectivo para deformaciones mecánicas longitudinales. Si utilizamos un material magnetoestrictivo como el terfenol, el cual responde a cambios lineales de deformación con el cuadrado del campo magnético en la dirección de este [2], para pequeñas intensidades de campo será posible escribir la ecuación (2) como [3,4,5]:
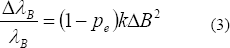
donde k es una parámetro relacionado con el magnetostrictivo. El montaje experimental utilizado se muestra en la Figura 1. El magneto-estrictivo empleado es fabricado por la compañía Adaptronic y sus especificaciones se pueden encontrar en la referencia [6]. A una barra de dicho material se le adhirieron dos FBGs separadas una distancia de 1.4cm con el propósito de observar la deformación del terfenol en diferentes puntos de la muestra. La longitud de cada FBG era de aproximadamente 5mm y una reflectividad del 100%. Se utilizo un imán en forma de anillo para producir el campo magnético que afectaba el comportamiento del magneto-estrictivo. Durante la experiencia se mantuvo las redes a temperatura de 20°C; por lo tanto podemos despreciar cualquier efecto de temperatura sobre las redes.
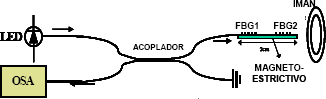
Figura 1. Configuración del montaje experimental realizado para medir campo magnético con redes de Bragg
Figure 1. Developed experimental setup to measure magnetic field using fiber Bragg grating
El comportamiento de lB en FBG1 y FBG2 en función del cuadrado del campo magnético para la región lineal cercana al origen se muestran en las Figura 2 y Figura 3 respectivamente.
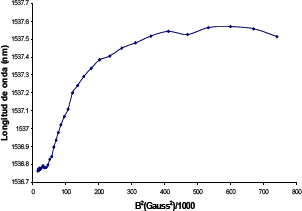
Figura 2. Respuesta FBG1 como sensor de campo
Figure 2. Response of the FBG1 sensor as a function of magnetic field
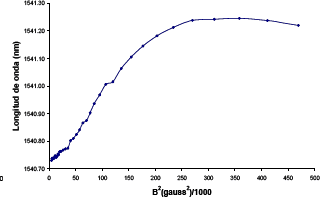
Figura 3. Respuesta FBG2 como sensor magnético de campo magnético
Figure 3. Response of the FBG2 sensor as a function of magnetic field
De las Figuras 2 y 3; las cuales tienen una incertidumbre de 2pm en la longitud de onda y 0.2G2 en B2; se observan que para campos magnéticos pequeños, hasta aproximadamente 150000 Gauss2, el cambio en la longitud de onda de Bragg, es proporcional al cuadrado del campo, con sensibilidades alrededor de 4.07644x10-6 nm/(G2x1000). Además, es posible ver que la linealidad se conserva a pesar de estar las redes colocadas en posiciones diferentes. Por lo tanto, esta técnica resulta ser útil para el diseño de sensores de campo magnético; aplicación ésta de gran interés en sistemas eléctricos.
2.3 Sensor de Temperatura
En condiciones de no deformación mecánica es posible demostrar que el corrimiento espectral de la longitud de onda de Bragg, según la ecuación (1) está dada por [1]:
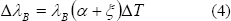
donde 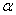 es el coeficiente de expansión térmica del silicio y
es el coeficiente de expansión térmica del silicio y 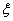 es el coeficiente termo-óptico. De aquí que es posible la construcción de un sensor de temperatura con el monitoreo del corrimiento espectral de la respuesta de la red de Bragg. Además es importante notar que se espera un comportamiento totalmente lineal con los cambios térmicos.
es el coeficiente termo-óptico. De aquí que es posible la construcción de un sensor de temperatura con el monitoreo del corrimiento espectral de la respuesta de la red de Bragg. Además es importante notar que se espera un comportamiento totalmente lineal con los cambios térmicos.
Para llevar a cabo la interrogación de la red se utilizó la técnica conocida como filtro fijo. El principio de la técnica se puede explicar considerando la Figura 4. La luz de un LED banda ancha ilumina mediante el acoplador direccional la FBG de referencia reflejándose parte del espectro del LED. La señal reflejada pasa nuevamente por el acoplador direccional iluminando la FBG sensora, que a su a vez refleja parte del espectro proveniente de la FBG de referencia; así, la potencia óptica medida por un fotodetector resulta ser proporcional a la convolución (área de intersección) entre los espectros de las redes. De esta manera, cambios en la separación relativa de los espectros de las redes se traducen en cambios de lectura de potencia óptica en el fotodetector.
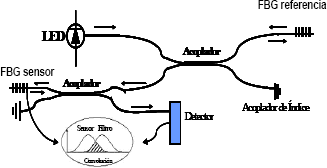
Figura 4. Montaje experimental de la técnica de filtro fijo
Figure 4. Experimental setup for the fixed filter technique
Siguiendo el montaje en la Figura 4, donde se utilizaron acopladores marca Newport 50/50, un medidor de potencia óptica marca EXFO, LED a 1550nm y ancho de banda de 50nm. Las redes de Bragg utilizadas como filtro y sensor poseen las siguientes características: Longitud de onda de Bragg 1550.49nm y 1549.27nm, respectivamente, ancho espectral de 2.7nm y 2.8nm y reflectividades del 40%. Para producir cambios de temperatura sobre la FBG sensora, la red se insertó en un calorímetro con agua, que inicialmente estaba a una temperatura de 7°C, la cual aumenta por medio de una bombilla insertada al calorímetro. La medida de temperatura se hizo por medio de una termocupla previamente calibrada. Los resultados obtenidos de curva de calibración e histéresis para el sensor de temperatura se muestran en las Figuras 5 y 6 respectivamente. La incertidumbre en las mediciones de potencias es de 0.1nw y 0.1°C en las mediciones de temperaturas.
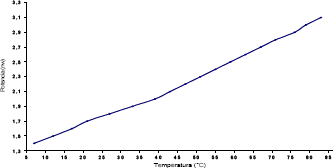
Figura 5. Curva de calibración para el sensor de temperatura
Figure 5. Calibration for the temperature sensor
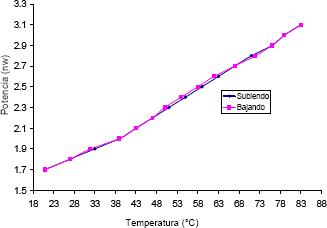
Figura 6. Análisis de histéresis para el sensor de temperatura
Figure 6. Hysteresis analysis of the temperature sensor
3. HERRAMIENTAS COMPUTACIONALES
3.1 Generalidades
El desarrollo acelerado de las computadoras y el estudio de los diferentes métodos numéricos han hecho de la simulación computacional una herramienta fundamental en procesos de investigación y desarrollo tanto en áreas de las ciencias básicas como de las ingenierías. Para problemas con estructuras complejas, como es el caso de las guías de onda ópticas micro-estructuradas, las soluciones analíticas se complican excesivamente, por lo que se hace imprescindible el desarrollo de un software que, por una parte, proporcione soluciones completas a partir de la discretización en problemas más simplificados y, por otra, que le sea posible la incorporación de nuevas herramientas de análisis a medida que se tienen nuevos desarrollos tecnológicos. Con esta filosofía se ha venido desarrollando el programa PHOENIXOWA (Optical Waveguide Analysis) para analizar la propagación característica de la luz en guías de onda dieléctricas con cualquier estructura transversal. En esta sección se referencian resultados obtenidos con PHOENIXOWA y se detalla algunas de las características del software en sí mismo, como también del proceso de discretización y de análisis de guías de onda en general. En el programa se implementaron técnicas matemáticas bien conocidas, como el método de diferencias finitas, el método de los elementos finitos (FEM), técnicas para graficación, entre otras.
3.2 Descripción del software
PHOENIXOWA incorpora varias técnicas numéricas, en particular, el método de los elementos finitos (FEM) para el cálculo de las constantes de propagación y las distribuciones de campo eléctrico (o magnético), y el método de diferencias finitas para evaluar el factor de corrección por efectos de polarización, el parámetro de dispersión y el inverso de la velocidad de grupo. En el caso del método de los elementos finitos, es deseable poder calcular las constantes de propagación y las distribuciones de campo con el menor número de operaciones posibles. Este objetivo se logra enumerando adecuadamente los nodos y discretizando con el menor número posible de elementos la sección transversal del guía de onda a analizar; lo que en parte se puede llevar a cabo mediante el uso de algunas herramientas que brindan programas comerciales basados en elementos finitos como son el AnsysÒ y CosmosÒ.
PHOENIXOWA proporciona un GUI (Graphic User Interface) para facilitarle al usuario la entrada de parámetros y el manejo de resultados de la simulación; además, integra un programa núcleo que se encarga de implementar la técnica de elementos finitos. El funcionamiento de PHOENIXOWA se puede dividir en tres etapas principales: pre-proceso, proceso y pos-proceso.
En el pre-proceso se define la malla de elementos finitos a utilizar, Figura 7, la cual se consigue mediante, por ejemplo, el programa comercial AnsysÒ que, además, puede brindar información de deformaciones termo-mecánicas cuando se requiera incorporar la parte estructural. Las propiedades de los materiales como son los índices de refracción de cada región del guía, la longitud de onda de la luz con la cual se va a trabajar, el número y tipos de modos de propagación a calcular, y otras opciones más de cálculo, se definen a través de las ventanas mostradas en la Figura 8. El proceso es la parte en la cual el programa núcleo ejecuta el cálculo utilizando el método de los elementos finitos escalar, del cual se hablará en la siguiente sección. A este programa se le entrega una serie de archivos que poseen la información de la discretización de la estructura de la sección transversal del guía de onda, de los índices de refracción, de la longitud de onda y de otras opciones más. Luego, el programa entrega otra serie de archivos que poseen las constantes de propagación, la distribución de los campos y otros parámetros de interés. El pos-proceso es la parte final del análisis por elementos finitos. En él podemos hacer cálculos adicionales, como son las velocidades de grupo, la dispersión y las correcciones necesarias. También podemos ver los resultados en archivos de texto o gráficamente. En esta parte podemos ver la superficie o el degradado en intensidad de la distribución del campo, las curvas de índice efectivo, del inverso de la velocidad de grupo y de la dispersión, Figura 9.
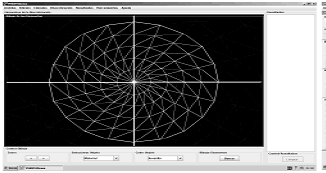
Figura 7. Malla de discretización típica de la sección transversal de un guía de onda, creada con AnsysÒ
Figure 7. Typical discretization of a waveguide cross section created by AnsysÒ
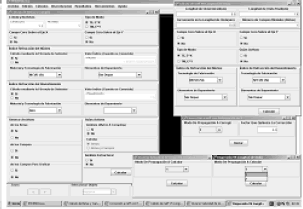
Figura 8. Ventana de opciones adicionales que ofrece PHOENIXOWA
Figure 8. Window of additional option displayed by PHOENIXOWA
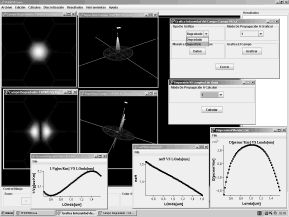
Figura 9. Representación gráfica de resultados que ofrece el programa PHOENIXOWA
Figure 9. Graphical representation offered by PHOENIXOWA for final results
3.3 Análisis de fibras ópticas micro-estructuradas
Desde la introducción de los cristales fotónicos a fibra [7], se han realizado diferentes estructuras que guían señales ópticas utilizando arreglos de huecos micro-estructurados [8]. En estas estructuras, el índice de refracción efectivo de los modos propagantes es un parámetro esencial, pues determina, entre otras, las propiedades de dispersión de la guía de onda.
La gran variedad de posibles formas y arreglos para los huecos demandan el uso de métodos numéricos que permitan modelar adecuadamente la sección transversal de estas estructuras para analizarlas. Adicionalmente, la existencia de interfaces con alto contraste en el índice de refracción entre el material con que se fabrican (generalmente Silicio puro) y los huecos, hace necesaria considerar una solución vectorial para tomar en cuenta los efectos de polarización del campo óptico. Entre las técnicas propuestas, el método de elementos finitos (FEM) se ha utilizado exitosamente, debido a que puede modelar cualquier geometría que tenga la guía de onda y a que se han desarrollado diferentes formulaciones vectoriales. Dentro de estas aproximaciones, existen las que se formulan en término de todas las componentes del campo eléctrico, o magnético, en donde se debe introducir una función de penalidad con coeficientes artificiales para eliminar las soluciones espurias que aparecen mezcladas con las soluciones físicamente aceptables [9]; es decir, en estos esquemas la exactitud de la solución depende de dicha penalidad. Este problema fue recientemente resuelto con elementos de bode de orden superior [10,11], haciendo posible la solución de la ecuación de onda vectorial a costa del aumento de la complejidad del algoritmo, y por ende, demandando altos requerimientos computacionales y mayor tiempo de procesamiento.
Como una alternativa más eficiente a las soluciones vectoriales, algunos de los autores propusieron [12] mejorar la aproximación escalar para ampliar su rango de validez a longitudes de onda largas y fracciones de llenado de aire grandes en fibras cristal fotónico, incluyendo en el análisis por el método de elementos finitos escalar (SFEM), un término de corrección que da cuenta de los efectos de polarización generados por las interfases material-hueco. Para este propósito se usaron elementos triangulares de primer orden, cuya región que delimitan es de índice de refracción homogéneo, y se aprovecha el hecho de que el SFEM provee directamente la distribución del campo sobre la sección transversal de la fibra para la corrección al análisis escalar.
Con este software, miembros del grupo han analizado exitosamente fibras de cristal fotónico [12,13], y otras más que incluyen efectos mecánicos y termo-mecánicos [14].
4. FABRICACION DE FUENTES DE LUZ A FIBRA OPTICA
4.1 Generalidades
Las fibras ópticas dopadas con Erbio (EDF) han sido ampliamente estudiadas por su emisión característica en la tercera ventana de transmisión por fibras ópticas, que las convierte en un elemento de sumo interés en la construcción de amplificadores ópticos y fuentes de luz láser [15].
Los modelos teóricos usados para el diseño y posterior construcción de dispositivos basados en fibras ópticas dopadas con Erbio se han basado tradicionalmente en parámetros espectroscópicos cuya medición no es práctica por los altos requerimientos tecnológicos [16]; esto en algunos casos es un limitante para el diseño optimizado de dispositivos basados en estas fibras. En este trabajo se ilustra una técnica alternativa para el diseño de una cavidad láser lineal a fibra óptica basada en Redes de Bragg.
4.2 Modelo del Láser Lineal A Fibra Óptica
Previamente en la referencia [17] hemos mostrado que es posible expresar las ecuaciones básicas para un Amplificador Óptico a fibra como se muestra a continuación:
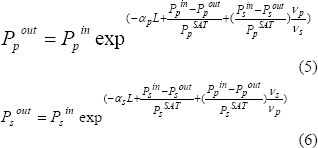
Las ecuaciones (5) y (6) representan el principal resultado de la teoría del amplificador óptico a fibra ya que su solución lleva a encontrar la potencia de salida a la longitud de onda de la señal para cada potencia de bombeo de entrada. Lo interesante de estas expresiones es que están dadas en términos de parámetros fácilmente medibles como se muestra en [18] lo que hace inmediato la identificación de parámetros de diseño certeros para un amplificador óptico. De otro lado si pensamos en un láser como un medio amplificador de luz realimentado podremos tener el modelo de un láser a fibra óptica.
El esquema típico de un láser lineal es mostrado en la Figura 10. Un láser a fibra óptica lineal está constituido básicamente por dos espejos de reflectividades R1 y R2 en los extremos de un tramo de fibra dopada con Erbio. Ambos espejos son transparentes a la longitud de bombeo así que el bombeo pasa una sola vez a través de la fibra. Para efectos de modelamiento se suponen dos regiones de perdidas (ξ1, ξ2) asociadas a elementos de sintonización y estabilización [19].
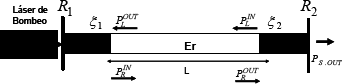
Figura 10. Esquema básico de un láser a Fibra óptica lineal
Figure 10. Basic configuration of a linear fiber laser
Si se evalúa el proceso de amplificación de luz después de un ciclo en la cavidad, es posible demostrar que la potencia de salida se puede escribir como:
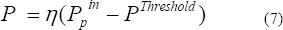
donde la ecuación (7) tiene la forma de la potencia para una fuente láser y por lo tanto esta dada en términos de una eficiencia 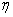 y una potencia de bombeo umbral
y una potencia de bombeo umbral 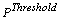 .
.
Las equivalencias en términos de los puntos fáciles de [20] para los parámetros de la ecuación (7) se pueden verificar en [19].
4.3 Resultados Experimentales Láser Lineal
La metodología de caracterización descrita en [19] se llevó a cabo con una fibra fabricada por Telebras-Brasil. En la Figura 11 se ilustra una de las curvas experimentales obtenidas para la caracterización a 1550nm.
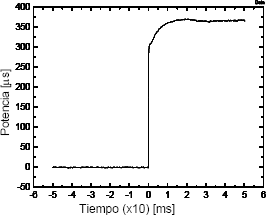
Figura 11. Resultado experimental para una fibra óptica dopada con Er
Figure 11. Experimental results for an Er-doped fiber optics
Con las curvas obtenidas a 1550nm y 980nm fue posible identificar los puntos fáciles y los tiempos característicos del sistema a 1550nm y a 980nm lo que permitió el cálculo directo de los parámetros de las ecuaciones (5) y (6).
Como la configuración lineal es una topología donde las pérdidas son bajas [21], se exploró experimentalmente una cavidad lineal donde los espejos reflectores fueron dos redes de Bragg de alta reflectividad. El esquema utilizado para el montaje se ilustra en la Figura 12.
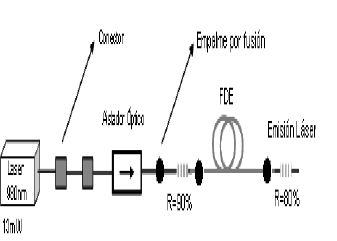
Figura 12. Montaje experimental desarrollado para la caracterización de fibras ópticas dopadas con Er
Figure 12. Developed experimental setup for the characterization of Er-doped fiber optics
Para el montaje experimental se dispuso de un láser Q-Photonics el cual ofreció una potencia de salida de 13mW para el que en condiciones óptimas se necesitaban 37m de FDE según el modelo
Con el montaje experimental descrito fue posible obtener 300µW de potencia de salida en 1551.5nm. En la Figura 13 se muestra el espectro de salida el cual fue medido con un Burleigh Multi-line Wavemeter WA-7600 que es un equipo de alta tecnología que tiene resolución de 1pm. Los resultados experimentales estuvieron de acuerdo con los modelos desarrollados con un error de 0,5 dB; de lo que se puede concluir que el modelo propuesto a pesar de ofrecer un camino muy simplificado desde el punto de vista del diseño de las cavidades ofrece resultados muy confiables.
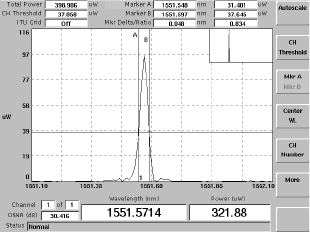
Figura 13. Espectro de emisión del láser a fibra óptica lineal
Figure 13. Spectral emission of the developed linear fiber laser
5. CONCLUSIÓN
En este trabajo se mostraron algunos de los desarrollos del Grupo de Fotónica y opto-electrónica. Se presentó la forma en que el Grupo lleva a cabo procesos de Ingeniería desde la Física en el ámbito de los sistemas a fibra óptica; lo que lo convierte en pionero en nuestro país y uno de los principales referentes latinoamericanos al lado de grupos de Brasil y Argentina.
6. AGRADECIMIENTOS
Este trabajo fue parcialmente financiado por Colciencias (Código: 1118-330-18905) y el proyecto DIME – Universidad Nacional de Colombia sede Medellín, código 30802951.
REFERENCIAS
[1] ANDREAS OTONOS, Fiber Bragg Grating, Review Article, AMERICAN INSTITUTE OF PHYSICS., pg 4309.1997. [ Links ]
[2] SANDLUND, L., FAHLANDER, M., CEDELL, T., CLARK, A. E., RESTORFF, J. B., AND WUN-FOGLE, M., Magnetostriction, elastic moduli, and coupling factors of composite Terfenol-D ,. Journal of Applied Physics, 75, pp. 5656-5658. 1994. [ Links ]
[3] J. L. CRUZ, A. DÍEZ, M. V. ANDRÉS, A. SEGURA, B. ORTEGA, AND L. DONG, Fiber Bragg gratings tuned and chirped using magnetic fields, Electron. Lett., vol. 33, no. 3, pp. 235–236. 1997. [ Links ]
[4] RACHID GAFSI AND MAHMOUD A. El-Sherif. Analysis of Induced-Birefringence Effects on Fiber Bragg Gratings, OPTICAL FIBER TECHNOLOGY 6, pg 299.1999. [ Links ]
[5] J. MORA, A. DÍEZ, J. L. CRUZ, AND M. V. ANDRÉS., A Magnetostrictive Sensor Interrogated by Fiber Gratings for DC-Current and Temperature Discrimination, IEEE Photonics Techn. Lett., vol. 12, Decembre 2000. [ Links ]
[6] A study of active engine mounts. Available: http://www.diva-portal.org/ [Julio 8 de 2007]. [ Links ]
[7] J. C. KNIGHT, T. A. BIRKS, P. S. J. RUSSELL, AND D. M. ATKIN, All-silica single-mode optical fiber with photonic crystal cladding, Opt. Lett. ,21, 1547-1549, 1996. [ Links ]
[8] P. RUSSELL, Photonic Crystal Fibers, Science, 299, 358-362, 2003. [ Links ]
[9] B. M. A. RAHMAN AND J. B. DAVIES, Penalty function improvement of waveguide solution by finite elements, IEEE Trans. Microwave Theory Tech., MTT-32, 922-929, 1984. [ Links ]
[10] M. KOSHIBA AND Y. TSUJI, Curvilinear hybrid edge/nodal elements with triangular shape for guided-wave problems, J. Lightwave Technol., 18, 737-743, 2000. [ Links ]
[11] M. KOSHIBA, S. MARUYAMA, AND K. HIRAYAMA, A vector finite element method with the high-order mixed-interpolating-type triangular elements for optical waveguides problems, J. Lightwave Technol., 12, 1547-1549, 1996. [ Links ]
[12] V. H. ARISTIZABAL, F. J. VÉLEZ, AND P. TORRES, Modelling of photonic crystal fibers with the scalar finite element method, Proc. SPIE, 5622, 849-854, 2004. [ Links ]
[13] V. H. ARISTIZÁBAL, P. TORRES, Analysis of photonic Crystal Fibers: Scalar Solution and polarization correction. Optics Express Vol. 14, pp. 11848-11854, 2007. [ Links ]
[14] F. J. VELEZ, V. H. ARISTIZÁBAL AND P. TORRES, Numerical model and analysis of optical fibers with internal electrodes. Revista Colombiana de Física, Vol. 38, No. 1, p.173-176 2006. [ Links ]
[15] E. DESURVIRE, J SIMPSON, Amplification of spontaneous emission in Erbium-doped single-mode fibers, Journal of Lightwave Technology, 7, 835-845, 1989. [ Links ]
[16] E.DESURVIRE, Erbium-Doped Fiber Amplifiers - Principles and Applications, John Wiley & Sons, Inc. New York, 1994. [ Links ]
[17] JORGE A. GÓMEZ, PEDRO TORRES, Láser de fibra óptica en anillo: modelo basado en parámetros de transmisión. Univesidad Nacional de Colombia. Sede Medellín. IX ENO. Medellín 2005. [ Links ]
[18] H.L.FRAGNITO E C.MAZZALI, Modelamento Analítico da Dinâmica de Ganho em Amplificadores a Fibra Dopada com Érbio - Relatório Técnico 12/96 - ContratoUnicamp-PADCT n°0730/91. [ Links ]
[19] C. BARNARD, P. MYSLINSKY, J. CHROSTOWOSKY, Analytical Model for Rare Earth Doped Fiber Amplifiers and Lasers, IEEE Journal of Quantum Electronics, 30, 1817-1830, 1994. [ Links ]
[20] JORGE A. GÓMEZ, PEDRO TORRES, ADRIANA C. TRIQUES, CARLA KATO, ALEXANDRE RIBEIRO Erbium doped fibers: characterization through the easy points method. 1Physics School, Universidad Nacional de Colombia-Sede Medellín. Mechanical Engineering Department, Pontifícia Universidade Católica do, Rio de Janeiro, Brazil Revista Colombiana de Física Vol. 38, Nº 2, p.p. 637-640. [ Links ]














