Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.72 no.157 Medellín Jan./Apr. 2009
LA EFICIENCIA TÉCNICA COMO UN NUEVO CRITERIO DE OPTIMIZACIÓN PARA LA GENERACIÓN HIDROELÉCTRICA A CORTO PLAZO
TECHNICAL EFFICIENCY AS A NEW APPROACH TO HYDROELECTRIC GENERATION IN THE SHORT TERM
JAVIER DIAZ
Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, javidiaz@unalmed.edu.co
Recibido para revisar marzo 13 de 2008, aceptado agosto 29 de 2008, versión final septiembre 12 de 2008
RESUMEN: En este artículo se formula un modelo no lineal para representar la eficiencia técnica en la operación de las turbinas de generación hidroeléctrica, partiendo de las gráficas entregadas por sus fabricantes, normalmente conocidas como diagramas colinares. Se propone un análisis de regresión, no lineal, múltiple para representar la eficiencia de una turbina Francis como una función cuadrática de la cabeza neta y la descarga de agua. Se postula una trayectoria de máxima eficiencia relativa, que permite encontrar la descarga óptima para una cabeza neta dada, la cual puede observarse en el diagrama colinar y calcularse de forma analítica con la función estimada. Se analiza la utilidad de esta trayectoria para la toma de decisiones con respecto a la descarga, como variable de decisión, para una empresa de generación hidroeléctrica operando a máxima eficiencia en el mercado de corto plazo.
PALABRAS CLAVE: cabeza neta, descarga, eficiencia de las turbinas, generación hidroeléctrica, optimización, trayectoria de máxima eficiencia relativa.
ABSTRACT: In this paper a non linear model to represent the technical efficiency in the hydroelectric generation turbine operation is formulated, beginning from graphs, given for the manufacturers, normally known as hill diagrams. A multiple non linear regression analysis is proposed to represent a Francis turbine as a quadratic function of the net head and the discharged water. A relative efficiency maximum trajectory to meet the optimal discharge to a specified net head is postulated, which can be observed in the hill diagram and calculated in an analytic form from the estimated function. It is analized this trajectory usefulness for decision making in regard to the discharge, as a decision variable, for a hydroelectric generation enterprise operating in the maximum efficiency in the short term market place.
KEY WORDS: net head, discharge, turbine efficiency, hydroelectrical generation, optimization, relative maximum efficiency trajectory.
1. INTRODUCCIÓN
En los sistemas de generación de potencia eléctrica, la Coordinación Hidrotérmica de Corto Plazo es concebido como un problema complejo, de optimización dinámica, estocástica, a gran escala. Este problema está asociado a la toma de decisiones con respecto a la generación de energía eléctrica asignada a cada una de las plantas, hidráulicas y térmicas, durante cada período del horizonte de planeación. En la operación del sistema deben satisfacerse, además de las condiciones de balance hídrico temporal y espacial, ciertas restricciones técnicas como el almacenamiento de agua en los embalses y las capacidades tanto de las plantas de generación como de las líneas de transmisión.
Para la solución de este problema se han considerado básicamente dos enfoques. En los esquemas tradicionales, basados en sistemas monopólicos centralizados, la función objetivo era el mínimo costo total esperado de la operación del sistema para todo el horizonte de planeación. En los sistemas desregulados, en esquemas de mercados en competencia, generalmente, se tiene como principal objetivo la maximización del beneficio de la empresa de generación.
En este trabajo se propone, como criterio de optimización, la máxima eficiencia en la operación de las unidades de generación hidroeléctrica. Este criterio se aplica a un caso de estudio donde se toma un sistema de generación de caída media, operado por una turbina Francis, con el objetivo de ilustrar la proposición de que en la programación de la operación de una central hidroeléctrica es posible y conveniente considerar la eficiencia de los recursos hidráulicos utilizados para la generación de electricidad.
Los esquemas tradicionales, normalmente, se basan en un concepto de costo de sustitución, de energía termoeléctrica por hidroeléctrica, y en un costo de oportunidad, estimado con base en escenarios hidrológicos y de almacenamiento de agua en los embalses. Para la solución del problema, se formula una función de costos futuros, FCF, que se utiliza para determinar la cantidad de agua que debe usarse en el período actual y la que debe ahorrarse para posterior utilización [1]. En el presente trabajo, se considera que las señales de largo y de mediano plazo, de un sistema agregado, pueden incluir una gran componente de incertidumbre, causando problemas de confiabilidad en la toma de decisiones para un sistema particular, como es el caso de interés de una empresa de generación hidroeléctrica. Por lo tanto, se considera importante realizar un análisis complementario de corto plazo que permita ajustar las citadas señales de mediano y de largo plazo.
La idea fundamental de este enfoque es aplicar herramientas de análisis estadístico y de optimización para hacer un uso racional y eficiente de los recursos hidráulicos en la operación de la central hidroeléctrica. El detallado modelamiento del sistema de generación hidroeléctrica podría contribuir a mejorar el aprovechamiento de los recursos hídricos que en ciertos momentos llegan a ser críticos para el abastecimiento de la energía necesaria en el desarrollo económico y social de las comunidades. Estos recursos hidroeléctricos pueden ser considerados como una fuente renovable de energía que contribuye a reducir el uso de combustibles fósiles, no renovables, y a evitar daños ambientales procedentes de las emisiones de contaminantes de las plantas térmicas. El uso racional y eficiente de estos recursos podría tener efectos significativos en la disminución del precio de la electricidad con sus consecuentes beneficios para la población.
El problema de Coordinación Hidrotérmica de Corto Plazo está relacionado con tres problemas, que, en este contexto, para el caso de una central hidroeléctrica, podrían especificarse como: i) El Despacho Económico Hidroeléctrico, HED, relacionado con la respuesta a la pregunta: cuánto generar, de manera óptima, considerando la máxima eficiencia de las unidades; ii) La Asignación de las Unidades Hidroeléctricas, HUC, asociado a la pregunta: cuándo generar, a máxima eficiencia, es decir, la asignación de las unidades o la decisión de cuándo encenderlas y cuándo apagarlas; y iii) El Diseño o la Preparación de Ofertas al mercado.
Estos problemas han sido abordados mediante técnicas como la Programación Lineal, PL, que indiscutiblemente presenta muchas ventajas, como la facilidad para la formulación y solución del modelo, aún para problemas de gran escala y acoplados en tiempo y espacio, la disponibilidad en el mercado de algunos de los paquetes de software, populares y transparentes al usuario, y la facilidad, claridad y utilidad en la interpretación de los resultados.
La estrategia de descomposición por cortes de Benders es normalmente utilizada cuando se presentan variables complicantes, aquellas cuya presencia agrega significativa complejidad al problema. La Programación Dinámica Dual Estocástica, SDDP, [1], implementada en el paquete de software MPODE, ha sido concebida como una función recursiva, actualizada a partir de soluciones duales de programación lineal. De esta manera se van obteniendo aproximaciones lineales a la función recursiva, evitando la conocida maldición de la dimensionalidad presente en la Programación Dinámica por la naturaleza combinatoria explosiva cuando crece el número discretizaciones de las variables de estado.
Mediante el enfoque propuesto en este trabajo, el problema del despacho económico de las unidades de generación hidroeléctricas, asociado a la pregunta ¿cuánto generar? puede resolverse a partir de la descarga óptima, de máxima eficiencia relativa, para una determinada cabeza neta, tal como se especifica mas adelante.
Este artículo está organizado como sigue. En la sección 2 se formula un modelo no lineal, para representar la generación hidroeléctrica en función de la cabeza neta y la descarga de agua, partiendo del análisis de un diagrama colinar entregado por el fabricante de la turbina. En la sección 3 se postula, como hipótesis de trabajo, una trayectoria de máxima eficiencia relativa conformada por la descarga óptima asociada a una determinada cabeza neta, y se intoduce una regresión cuadrática bivariable como método de análisis estadístico. El procedimiento propuesto se ilustra, en la sección 4, mediante un caso de estudio. En la sección 5 se estima la trayectoria de máxima eficiencia relativa mediante análisis matemático. En la sección 6 se presentan posibles extensiones de este enfoque, se esbozan lineamientos para una posible solución del problema de Asignación de las Unidades Hidroeléctricas y se plantea, como trabajo futuro, el diseño de ofertas para someter al mercado del día siguiente. Finalmente se presentan las conclusiones, en la sección 7, las referencias y un anexo con los procedimientos estadísticos.
2. DEFINICIÓN DEL PROBLEMA: LA GENERACIÓN HIDROELÉCTRICA COMO UNA FUNCIÓN NO LINEAL DE LA CABEZA NETA Y LA DESCARGA
Las unidades de generación hidroeléctrica presentan un comportamiento operacional complejo. Su potencia de salida depende básicamente de tres variables, a saber, la cabeza neta, la descarga de agua a las turbinas y la eficiencia técnica del conjunto turbina-generador. La cabeza neta es una función no lineal de variables tales como la cabeza bruta (relacionada con el volumen almacenado de agua en el embalse), el flujo de agua descargado a las turbinas y el nivel de agua en la cola del embalse. Además, la eficiencia de la turbina es una función no lineal de la cabeza neta y de la descarga de agua.
La potencia de salida de la unidad de generación hidroeléctrica j, Pj, en MW, puede escribirse como:
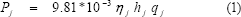
Donde: 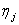 representa la eficiencia de las unidades, en porcentaje como una medida adimensional; qj la descarga de agua a la turbina, en m3/s; y hj, la cabeza neta, en m. La energía hidroeléctrica generada durante un intervalo de tiempo de duración t puede representarse como:
representa la eficiencia de las unidades, en porcentaje como una medida adimensional; qj la descarga de agua a la turbina, en m3/s; y hj, la cabeza neta, en m. La energía hidroeléctrica generada durante un intervalo de tiempo de duración t puede representarse como:
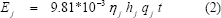
Considerar la cabeza neta variable, hj, para la estimación de la potencia generada en la operación de una central hidroeléctrica, puede tener un efecto significativo. En tal caso, la potencia de salida, Pj, y la energía hidroeléctrica generada, Ej, no son funciones lineales, como ha sido asumido en muchos trabajos relacionados, donde se consideran la cabeza neta y la descarga como parámetros con valores promedio para el período de tiempo de interés [2]-[5].
En este trabajo se formula un modelo no lineal para representar la operación de las turbinas. Se parte de la información disponible, entregada por sus fabricantes, generalmente como gráficas de eficiencia, a diferentes niveles, en términos de la cabeza neta y la descarga de agua, normalmente conocidas como diagramas colinares [6], tal como el que se ilustra en la Figura 1, adaptada por el autor de [7].
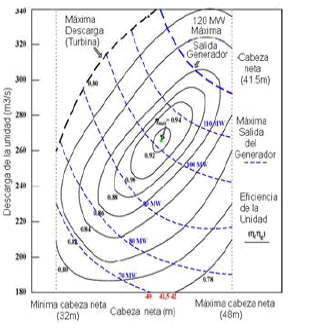
Figura 1. Eficiencia de una turbina Francis en función de la cabeza neta y la descarga de agua
Figure 1. Francis turbine efficiency as a net head and water discharge function
Del análisis de uno de los citados diagramas colinares, puede observarse que existe un punto de máxima eficiencia, aproximadamente 0.94, en este caso, correspondiente a unos parámetros de diseño, donde se presenta su desempeño óptimo, que serán llamados en este trabajo cabeza de diseño, hd, y descarga de diseño, qd, con valores aproximados de 41.67 m y 263.43 m3/s, respectivamente.
En este diagrama, para cualquier pareja (cabeza neta, descarga) asociada a cualquier punto de la región de operación factible, puede leerse tanto la eficiencia de la turbina como la potencia de salida.
Del análisis de la Figura 1 puede considerarse la eficiencia de una turbina Francis como una función cuadrática de la cabeza neta y la descarga de agua, tal como se presenta en (3). Además, debe tenerse en cuenta que la cabeza neta es función de varias variables entre las cuales se destaca, por su importancia, la descarga de agua a la turbina.
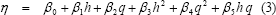
3. HIPÓTESIS DE TRABAJO Y MÉTODO DE ANÁLISIS
Mediante un detallado análisis de la Figura 1, puede inferirse esta hipótesis de trabajo:
Existe una trayectoria de máxima eficiencia relativa, que depende del nivel alcanzado por la cabeza neta, para el cual puede leerse, en el diagrama colinar, la descarga óptima, de máxima eficiencia relativa, que es posible alcanzar con la citada cabeza neta.
En la Figura 1 puede observarse que si se toma la cabeza neta dada, en el eje horizontal, dentro del rango de operación factible, a medida que incrementa la descarga, desde su límite inferior, aumenta la eficiencia de la turbina, hasta un nivel máximo, a partir del cual empieza a disminuir. Este es el punto de máxima eficiencia relativa para la cabeza neta dada. Si se permite la variación de la cabeza neta, dentro de su rango de operación factible, y para cada uno de sus valores se lee el correspondiente punto de máxima eficiencia, puede obtenerse la citada trayectoria de máxima eficiencia relativa. El punto de diseño, nominado en este trabajo como la pareja (hd, qd), pertenece a dicha trayectoria.
Con el fin de facilitar el análisis del sistema y su aplicación en la toma de decisiones, a partir del diagrama de curvas colinares, se realiza un trabajo estadístico que permite estimar la eficiencia de la turbina como una función cuadrática de dos variables: la cabeza neta y la descarga de agua. Su objetivo es estimar los coeficientes 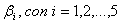 de la función cuadrática (3). Esta representación permitirá hallar, de manera analítica, la citada trayectoria de máxima eficiencia relativa.
de la función cuadrática (3). Esta representación permitirá hallar, de manera analítica, la citada trayectoria de máxima eficiencia relativa.
4. CASO DE ESTUDIO
Se considera como información de entrada el diagrama colinar de la Figura 1. Mediante el uso del visor de textos e imágenes GSview 4.7 para archivos Poscript, se tomó una muestra de 378 puntos. Con el uso del paquete estadístico R, versión 2.4.1, se obtuvo el siguiente modelo que cumple las pruebas estadísticas, t y F, y arroja un R2 ajustado de 0.82. (Ver Anexo)
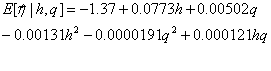
En la Figura 2 se presentan las gráficas de los puntos muestreados (arriba) y el modelo ajustado (centro y abajo). Para cualquier pareja (cabeza neta, descarga) asociada a cualquier punto de la región de operación factible, puede utilizarse la anterior ecuación para estimar la eficiencia de la turbina, ηj. Así mismo, es posible utilizar este valor de eficiencia para calcular tanto la potencia de salida, Pj, utilizando (1), como la energía generada, Ej, durante un intervalo de tiempo de duración t, aplicando (2).
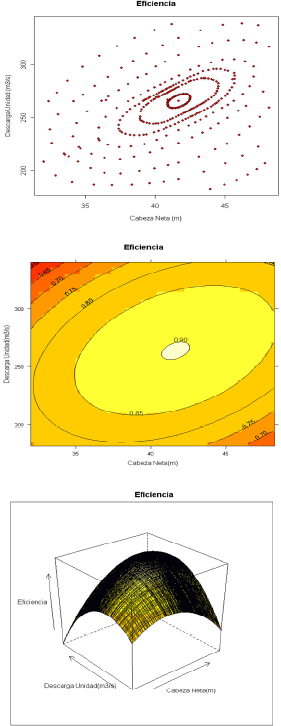
Figura 2. Puntos muestreados de la gráfica de eficiencia (arriba). Modelo ajustado (centro y abajo)
Figure 2. Sample points of the efficiency graphic (up). Fit model (center and down)
5. ESTIMACIÓN DE LA TRAYECTORIA DE MÁXIMA EFICIENCIA RELATIVA ANÁLISIS MATEMÁTICO
La ventaja de una función de este tipo consiste en la posibilidad de desarrollar un análisis matemático de optimización para su uso en decisiones relacionadas, por ejemplo, con la descarga óptima en los procesos operativos diarios u horarios (o, inclusive, para un menor intervalo de tiempo, según el diseño del sistema o mercado de interés). En estos períodos de tiempo, de muy corto plazo, es posible conocer, con buena aproximación, la cabeza neta, la cual puede actualizarse, mediante un proceso iterativo, de tal manera que permita la operación, a máxima eficiencia, de las unidades de generación. De este modo, podría obtenerse el mínimo costo de operación, desde el pùnto de vista del recurso hidráulico descargado para cubrir una determinada demanda o para la preparación o el diseño de las ofertas a someter al mercado del día siguiente.
Para el análisis de la operación del sistema en un período de tiempo dado, puede tomarse la cabeza neta como una variable exógena, ya que generalmente presenta poca variabilidad en el corto plazo. En este caso, la descarga de agua a la turbina representa la variable de decisión, de tal manera que para una cabeza neta dada, la eficiencia de la turbina es una función, no lineal, de la descarga. Las otras variables que determinan la cabeza neta, en general, pueden considerarse dependientes de la descarga y de algunos parámetros del sistema relacionados con la topología del embalse o con el diseño de la central hidroeléctrica.
La descarga óptima, para una cabeza neta dada, puede hallarse, mediante optimización, al igualar a cero la derivada parcial de la función de eficiencia con respecto a la descarga, δη / δq = 0 (para lo cual, h se toma como una constante), y resolviendo la ecuación resultante, para la descarga, q, como una función de la cabeza neta, h. En el caso de (3), se tiene:
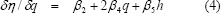
De (4), puede expresarse q como una función lineal de h, así:
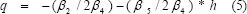
La eficiencia técnica de una turbina Francis, como la de la Figura 1, ha sido aproximada mediante un modelo cuadrático bivariable, como se especifica en (3), a partir del cual y mediante análisis matemático, se ha llegado a una función lineal que permite hallar la descarga de máxima eficiencia relativa asociada a una determinada cabeza neta. Para esta pareja es posible calcular tanto la eficiencia de la turbina como la potencia de salida y la energía generada, es decir, puede estimarse el nivel de potencia a máxima eficiencia relativa, lo cual puede servir a la empresa generadora como una ayuda importante para la toma de decisiones en el diseño de ofertas, relacionadas con las cantidades de energía, para someter al mercado de corto plazo.
Continuando el análisis matemático, mediante un procedimiento similar, igualando a cero la derivada parcial de la eficiencia, esta vez con respecto a la cabeza neta, δη / δh = 0, (tomando la descarga q como una constante), se obtiene:
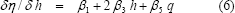
De los anteriores análisis, se tiene el sistema de dos ecuaciones lineales simultáneas, con dos variables, formado por (4) y (6), cuya solución debe reproducir el punto de diseño del diagrama colinar. Para el ejemplo numérico del caso de estudio se obtiene el sistema:
q = 131.4136 + 3.1675 * h
h = 29.5038 + 0.0462 * q
cuya solución, salvo errores de redondeo, reproduce el punto de diseño, observado en el diagrama colinar de la Fig. 1, (hd, qd) = (41.67, 263.43).
6. POSIBLES EXTENSIONES DE ESTE ENFOQUE
6.1 La operación del sistema
6.1.1 La Potencia como una función cúbica de la cabeza neta y la descarga
La ecuación (1) representa la Potencia de salida, Pj, de una turbina Francis, como función de varias variables. Si en (1) se reemplaza la eficiencia, expresada en (3) como una función cuadrática de la cabeza neta y la descarga, se obtiene la Potencia de salida, Pj, como una función cúbica de las mismas variables, así:
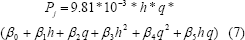
Normalmente, en la operación del sistema, se requiere generar una potencia dada P. La cabeza neta es conocida por las condiciones del embalse y de las unidades de generación. Por lo tanto, puede calcularse la descarga de operación, q, para generar la potencia deseada P, mediante la solución de la ecuación cúbica (7). Además, puede estimarse la eficiencia técnica asociada a esta pareja (cabeza neta dada, descarga calculada) aplicando (3).
6.1.2 Pérdida de eficiencia por descarga
Para cualquier punto de la región de operación factible, la pérdida de eficiencia por descarga, ocasionada por no operar la turbina a la descarga de máxima eficiencia relativa, para una determinada cabeza neta, h, puede calcularse como la diferencia entre las eficiencias estimadas, utilizando la descarga de máxima eficiencia relativa y la descarga de operación para generar la potencia de interés. Esta pérdida de eficiencia puede significar un mayor uso del recurso hídrico necesario para generar la potencia determinada.
6.2 El problema de Asignación de las Unidades de generación Hidroeléctrica. Análisis Dinámico
6.2.1 Evolución del nivel del embalse con las decarga
La energía eléctrica generada por la turbina, Ej, en MWh, puede calcularse como la potencia Pj, en MW, multiplicada por la duración del periodo de tiempo, t, en horas, según (2). En un análisis dinámico, la descarga, q, puede considerarse como una variable de decisión o de control, y la cabeza neta, h, como una variable endógena (dependiente tanto de las afluenciasde agua al embalse como de la descarga q).
Si se mantiene la descarga de agua a las turbinas, q, durante un periodo de tiempo de duración t, el volumen de agua descargada, q*t, usada para la generación de energía eléctrica, Ej, ocasiona la disminución del volumen almacenado en el embalse, así como la altura del agua contenida en él, o su cabeza bruta; por lo tanto, la cabeza neta asociada a la turbina puede empezar a decrecer. Dependiendo de la topología del embalse, la relación volumen-csbeza, suele representarse mediante curvas de nivel específicas. Utilizando las curvas típicas del embalse particular de interés puede actualizarse tanto el nivel de agua en el embalse, para un período de tiempo especificado, como su cabeza neta. Para esta última, es posible calcular la descarga de máxima eficiencia relativa, a la cual debería operar la turbina durante el siguiente período de tiempo, y nuevamente actualizar los parámetros: volumen y nivel de agua en el embalse, y cabeza neta, siempre que ésta permanezca en la región de operación factible. De esta manera, la cabeza neta podría disminuir de forma continua hasta su nivel mínimo permisible.
La descarga de agua a la turbina, idealmente, debería ir disminuyendo también de manera continua, para permanecer en la trayectoria de máxima eficiencia relativa en su dirección de descenso, según la cabeza neta actualizada. Sin embargo, para la operación de una central hidroeléctrica, en un caso práctico, podría ser más conveniente calcular la descarga de máxima eficiencia relativa, para una cabeza neta dada, y establecer un umbral de tolerancia para la cabeza neta, dentro del cual podría conservarse la descarga constante. Cuando la descarga neta caiga por fuera de los límites de este umbral de tolerancia, se actualizaría la descarga a un nuevo valor, de máxima eficiencia, para la nueva cabeza neta.
Dadas las características de la turbina Francis, especificadas en el diagrama colinar de la Fig. 1, y su eficiencia técnica estimada mediante (3), puede conocerse la pendiente de la trayectoria de máxima eficiencia relativa, m = δη / δq. En este caso m = – (β5/2β4). De tal manera, tomando las diferencias finitas, se tendría, Δq = m * Δh. Cuando Δh sea mayor que el umbral de tolerancia, especificado previamente, es posible actualizar la descarga, q, para operar a la máxima eficiencia relativa.
6.2.2 Considerando afluencias de agua al embalse
Las conocidas técnicas de Programación Lineal Entera Mixta, PLEM, que permiten combinar variables continuas, enteras y binarias en un mismo modelo, se han convertido en una poderosa herramienta para la formulación y solución de problemas de naturaleza muy diversa. La PLEM se concibe como una buena alternativa para la solución del problema de Asignación de las Unidades Hidroeléctricas, incluyendo su encendido y apagado, para lo cual pueden usarse los métodos de ramal y límite (Branch and Bound) o aproximaciones lineales por partes, utilizando variables binarias para identificar los segmentos lineales.
En un periodo de tiempo dado puede considerarse la alternativa de no generar, es decir, es posible tomar q = 0, lo cual tiene como efecto conservar el agua en el embalse, con la posibilidad de permitir el incremento de su nivel, durante el tiempo y, por lo tanto su cabeza neta, para utilizar el recurso hídrico en periodos futuros. De tal manera, en la formulación del problema, puede aparecer la descarga afectada por una variable binaria, Bt, que toma valores de 1, 0 si la decisión es generar o no generar, durante el período t.
Las afluencias de agua al embalse pueden provenir de la hidrología, así como de las descargas de otros embalses aguas arriba. En este último caso, si estos embalses son operados por la misma empresa será necesario integrar la toma de decisiones en la cadena para realizar una operación óptima del sistema. En el caso de que los embalses sean operados por una empresa diferente, será necesario recurrir a otras herramientas como la teoría de juegos.
Considerando pronósticos de entrada de agua al embalse, pueden asumirse afluencias, At, para cada periodo de tiempo t. Si este volumen total de agua disminuye, se debe regresar al caso anterior, donde se analiza la disminución de la cabeza neta con la descarga. De lo contrario, la cabeza neta debe actualizarse para este mayor volumen de agua. Si la cabeza neta permanece dentro de un umbral de tolerancia predefinido, se continúa la operación con la descarga dada; de otra manera, se actualiza la descarga de máxima eficiencia relativa. Este proceso continúa siempre que la cabeza neta siga siendo menor que la cabeza de diseño. En caso contrario, a medida que la cabeza se aproxima a la máxima, es conveniente realizar un análisis de riesgo de vertimientos para complementar la metodología propuesta de toma de decisiones sobre la utilización de la trayectoria de máxima eficiencia relativa.
6.3 El diseño de ofertas para someter al mercado del día siguiente.
Los ingresos de la empresa de generación son el producto de los precios de mercado de la energía y las cantidades que puede producir y vender a estos precios. La cantidad producida depende de las condiciones de operación, determinadas, entre otras, por la topología del embalse y las características de la central. La principal variable de decisión, en cuanto a la generación hidroeléctrica, es la descarga de agua a las turbinas. La metodología propuesta en este trabajo permite estimar la trayectoria de máxima eficiencia relativa mediante la cual puede obtenerse la descarga óptima para una determinada cabeza neta que se considera conocida en cualquier período de tiempo. Por otro lado, los pronósticos de los precios de la energía son una de las componentes fundamentales para el diseño de los precios de oferta para someter al mercado del día siguiente. Esta temática está fuera del alcance de este estudio pero debería ser retomada en posteriores trabajos.
7. CONCLUSIONES
En el enfoque tradicional, la política de operación del sistema hidrotérmico de mediano plazo es una combinación de pronósticos estocásticos de entrada, planificación de mantenimiento y modelación de factores económicos para el mercado futuro, entre otros. El proceso de programación hidroeléctrica diaria comienza con una evaluación de esta política de operación a mediano plazo para determinar la cantidad de agua a descargar, con base en pronósticos tanto del precio de mercado del día siguiente como de las afluencias al embalse. El resultado del proceso diario de operación óptima es un conjunto de descargas diarias de agua para cada planta, las cuales dependerán de los niveles reales del embalse, los pronósticos del flujo, las previsiones de mercado de corto y mediano plazo y el portafolio de contratos en que se ha comprometido la empresa [8].
En este estudio se considera un enfoque complementario, donde la modelación detallada de las características de las unidades de generación hidroeléctrica es de fundamental importancia para la planeación de su operación, ya que es necesario representar, con una buena aproximación, la relación entre el agua descargada y la potencia de salida, así como la energía hidroeléctrica generada. La formulación de un modelo analítico para representar esta relación tiene la ventaja de facilitar un tratamiento matemático para encontrar una trayectoria de máxima eficiencia relativa.
En este documento se ha tenido en cuenta la operación de las turbinas a una velocidad constante. Como trabajo futuro se plantea la consideración de su operación a velocidad variable.
REFERENCIAS
[1] PEREIRA M. AND PINTO L. Multistage stochastic optimization applied to energy planning. Mathematical Programming, vol. 52, 359-375, 1985. [ Links ]
[2] VELÁSQUEZ J.M., RESTREPO P.J., AND CAMPO R. Dual Dynamic Programming. A note on implementation. Water Resources, vol. 35, No.7, 2269-2271, 1999. [ Links ]
[3] CATALAO J.P.S., MARIANO S.J.P.S, MENDES V.M.F. AND FERREIRA L.A.F.M. Scheduling of head-sensitive cascaded hydro systems: a comparison based on numerical simulation results, Proceedings of the Fourth IASTED International Conference on Power and Energy Systems, Greece, 418–423, 2004. [ Links ]
[4] CATALAO J.P.S., MARIANO S.J.P.S, MENDES V.M.F. AND FERREIRA L.A.F.M. Parametrization effect on the behavior of a head depen dent hydro chain using a non-linear model, Electr Power Syst. 76, 404-412, 2006. [ Links ]
[5] CAMPO R. y RESTREPO P. Estudio de optimalidad del programa MPODE. Mundo Eléctrico, vol. 18, No 54, 32-35, 2004. [ Links ]
[6] HEREDIA F.J, AND NABONA N. Optimun short term hydrothermal scheduling with spinning reserve through network flows., IEEE Trans Power Syst., 10 (3), 1642-1651, 1995. [ Links ]
[7] FINARDI E.C. AND Da SILVA E.L. Unit Commitment of single hydroelectric plant, Elect. Power System Research, 75, 116-123, 2005. [ Links ]
[8] TUFEGDZIC N., FROWD R.J. AND STADLIN W.O. A Coordinated Approach for Real-time Short Term Hydro Scheduling. IEEE Trans. on Power Systems, vol. 11, No.4, 1698-1704, 1996. [ Links ]














