Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.72 no.157 Medellín Jan./Apr. 2009
MODELO AUTOREGRESIVO MULTIVARIADO BASADO EN REGÍMENES PARA LA GENERACIÓN DE SERIES HIDROLÓGICAS
CLASS BASED MULTIVARIATE AUTOREGRESSIVE MODEL FOR HYDROLOGICAL SERIES GENERATION
JULIAN MORENO CADAVID
Universidad Nacional de Colombia, Docente Escuela de Sistemas, Facultad de Minas, jmoreno1@unalmed.edu.co
JOSÉ ENRIQUE SALAZAR
Empresas Públicas de Medellín, Profesional Tecnología Mercados Energéticos, jose.salazar.velasquez@epm.com.co
Recibido para revisar febrero 4 de 2008, aceptado abril 11 de 2008, versión final abril 30 de 2008
RESUMEN: El objetivo de este artículo es presentar la utilización de un modelo autoregresivo multivariado para la generación de series hidrológicas sintéticas. Dicho modelo emplea como datos de entrada las series históricas de caudales pero además considera el uso de una variable exógena para la determinación de regímenes. Tal variable es la SST la cual está relacionada, no sólo estadística si no físicamente, con los caudales. A manera de ejemplo se muestra el desarrollo del modelo para tres ríos específicos del sistema hídrico Colombiano para un horizonte de largo plazo, empleando el pronóstico de mediano plazo de la NOAA para la SST.
PALABRAS CLAVE: Generación de Series Hidrológicas, Modelo de Thomas y Fiering, Modelo Autoregresivo Multivariado, SST.
ABSTRACT: The aim of this paper is to show the use of a multivariate autoregressive model for synthetic hydrologic series generation. Such model uses as input data the streamflows historical series but it also considers an exogenous variable for classes determination. This variable is the SST which is related, not just statistical but physically with the streamflows. As an example, the development of the model for three specific rivers of Colombian system is presented in a long term horizon, using the NOAAs SST medium term forecast.
KEYWORDS: Hydrological Series Generation, Thomas & Fiering Model, Multivariate Autoregressive Model, SST.
1. INTRODUCCIÓN
Dado el alto componente hidráulico del parque de generación en Colombia (cerca del 70% de la capacidad instalada corresponde a plantas de este tipo), la evolución de la hidrología desempeña un papel fundamental en la operación comercial de las plantas del sistema y por tanto en la formación del precio de la electricidad. Teniendo esto en mente, la modelación de las series hidrológicas resulta ser una tarea importante, no solo para las entidades encargadas de la planeación y operación del mercado (básicamente la UPME [7] y XM [9] respectivamente), si no también para las empresas involucradas que requieren bien sea evaluar la viabilidad de proyectos futuros, o proyectar los ingresos provenientes de sus plantas existentes. Este último caso con múltiples fines: elaboración de presupuesto, valoración de plantas, etc.
Un caso concreto que ejemplifica claramente la utilidad que para las empresas implica la modelación de dichas series es la reciente adopción en el mercado eléctrico colombiano del esquema de cargo por confiabilidad [2].
De esta manera muy resumida puede decirse que bajo este esquema una planta nueva debe participar en una subasta en la que compite con otras plantas por una remuneración que reciben a cambio de garantizar la entrega bajo ciertas condiciones del mercado de una cierta cantidad de energía conocida como obligación de energía firme. El resultado de dicha subasta es la determinación del valor de dicha remuneración o prima. Dentro de este contexto la pregunta que debe hacerse cada agente en este mercado es cuál debería ser el valor de esa prima para que la inversión en cada planta sea remunerada de manera adecuada, y de su respuesta depende la manera en la que participa en la subasta. Esa pregunta sin embargo no es fácil de responder pues cada agente debe considerar que sus ingresos provienen en una parte del cargo por confiabilidad, pero también por sus ingresos por ventas de energía en el mercado, los cuales a su vez está determinados por dos variables: cantidad de energía vendida y precio al que se vende. Y ese precio precisamente, tal como se indicó al principio de la introducción, está determinado en gran medida por la evolución de la hidrología.
El resto de este artículo se encuentra organizado de la siguiente manera. En la siguiente sección se describe brevemente la finalidad y fundamentos de la hidrología estocástica. En la sección 3 se presenta la formulación matemática del modelo empleado en este trabajo. En la sección 4 se describe el preprocesamiento que debe realizarse a los datos de entrada para mejorar el desempeño del modelo. En la sección 5 se explica como se puede incorporar una variable exógena (diferente a los caudales) en el modelo, y en la sección 6 se muestran los resultados obtenidos. Finalmente en la sección 7 se presentan las conclusiones.
2. HIDROLOGÍA ESTOCÁSTICA
El creciente número de aplicaciones en el área de los recursos hidráulicos ha exigido un estudio más detenido de los fenómenos hidrológicos, dando origen durante la década de los 70s a una disciplina conocida con el nombre de hidrología estocástica, cuyo fundamento es contemplar las variaciones aleatorias que presentan dichos fenómenos, para que luego sea posible estimar la influencia que estas variaciones tienen sobre las consecuencias físicas y económicas de diversos procesos hidráulicos [8].
Esta disciplina considera que los eventos hidrológicos ocurridos en el pasado, y los que tendrán lugar en el futuro, son funciones muestrales de procesos estocásticos muy complejos. Un proceso estocástico es una función aleatoria de un parámetro (usualmente el tiempo).
A manera de ejemplo, es posible considerar los caudales promedio en un cierto punto de un determinado río, y contemplar x(t) como el caudal del año t, siendo t un parámetro discreto. Supóngase que t = 1950, 1951, , 2007. Entre 1950 y 2007 se dispone de una función muestral que corresponde al registro histórico. El conjunto muestral existe únicamente como una abstracción de uso conceptual: está compuesto por aquellas funciones muestrales que pudieron haber ocurrido. Mirando hacia el futuro desde 2007, es posible imaginar todas las posibles (infinitas) funciones muestrales que podrán ocurrir, tal como se muestra en la Figura 1 (allí se han dibujado las funciones muestrales como un trazo continuo, aunque cabe recordar que t es discreto).
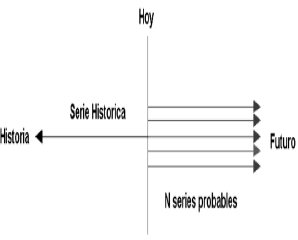
Figura 1. Generación de series sintéticas
Figure 1. synthetic series generation
El interés de la hidrología estocástica es encontrar modelos que proporcionen alguna idea sobre las posibles funciones muestrales, o mejor, sobre las variaciones muestrales de dichas series. Tales modelos permiten generar series de tiempo, conocidas generalmente como trazas sintéticas, que son estadísticamente indistinguibles de las series históricas en términos de ciertos estadísticos considerados como relevantes. Es importante destacar que estos modelos son meramente descriptivos, en el sentido estadístico, y no son modelos causales que pretendan explicar el carácter físico de los fenómenos hidrológicos.
El diseño de estos modelos es gobernado por dos hipótesis fundamentales. La primera es la hipótesis de la estacionariedad, se dice que un proceso es estacionario si sus propiedades estadísticas no cambian en el tiempo. Así por ejemplo, parece aceptable la suposición de que el proceso que da origen a la serie de caudales anuales de un río es estacionario, si se piensa en el carácter periódico anual de diversos eventos astronómicos que tienen influencia sobre ciertos procesos hidrológicos. Se diría, si tal es el caso, que la media, la varianza, etc. de la serie permanecen invariables a lo largo del tiempo. La segunda hipótesis, más fuerte que la primera y que en realidad la implica, tiene que ver con la llamada ergodicidad del proceso. Si se acepta esta hipótesis, los estadísticos de un determinado proceso pueden estimarse promediando a lo largo de una función muestral (la serie histórica), evitándose la necesidad de estimar, para un valor específico de t = ta, efectuando el promedio sobre el conjunto de funciones muestrales. Haciendo un ejemplo con caudales mensuales, la hipótesis de ergocidad permite afirmar que la media de x (enero de 2008), igual a la media x(ta) para todo ta en virtud de la estacionalidad del proceso, puede estimarse haciendo el promedio aritmético de los caudales de los eneros observados entre 1950 y 2007.
3. FORMULACIÓN DEL MODELO
Un primer modelo para la generación de caudales sintéticos fue desarrollado en 1962 por Thomas y Fiering [6]. Este modelo contempla además de la media y la varianza, el coeficiente de correlación pues estos autores consideraron que los registros históricos indicaban la importancia de preservar este estadístico (consecuencia del fenómeno de persistencia observable en los procesos hidrológicos). Su forma es la siguiente:
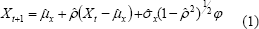
Donde φ es ruido aleatorio normal
La técnica de los valores esperados (empleada para definir los parámetros del modelo) dice que los estadísticos μx, σx y ρ son preservados como valores esperados. O sea que los estadísticos de una serie sintética como las ya definidas tienden a los correspondientes μx, σx y ρ cuando el número de términos de la serie tienda a infinito. Por eso se dice que las series sintéticas son estadísticamente indistinguibles de la serie histórica en términos de la media, la varianza y el coeficiente de correlación. Igualmente, se espera que las series sintéticas proporcionen alguna idea sobre las variaciones muestrales del proceso, lo que equivale a decir que se espera que las series sintéticas guarden algún grado de coincidencia con las series reales que podrán ocurrir en el futuro.
Hasta aquí, se presenta un modelo para la generación de series sintéticas para una sola variable, es decir, para un solo río. Sin embargo, la necesidad de preservar propiedades de correlación espacial de procesos hidrológicos que tienen lugar en sitios diferentes (varios ríos), dio origen a modelos que generan varias series sintéticas a la vez, cada una correspondiente a uno de los sitios considerados. En 1967, Matalas [4] propuso el siguiente modelo, desarrollado luego por Young & Pisano [10], que en realidad es una extensión del de Thomas y Fiering al caso de series múltiples:

En donde Xt es un vector columna de variables aleatorias, cada una de las cuales corresponde, por ejemplo, al caudal en el año t en uno de los z sitios diferentes; φ es un vector de z componentes aleatorias, independientes entre sí e independientes de las variables de Xt, cada una de las cuales tiene media cero y varianza unitaria (normalmente distribuida); A y B son matrices cuadradas de orden z. Para determinar A se tiene las siguiente ecuación:

En el caso de interés Sxx corresponde a la matriz de covarianza entre ríos (recordar que por definición la covarianza entre dos variables no es más que el promedio de los productos de las desviaciones de ambas variables respecto a sus medias respectivas), mientras que Syx corresponde a la matriz de covarianza entre ríos pero con un rezago de un período (un mes).
Por su parte B es una matriz que cumple con la siguiente propiedad:
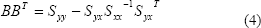
Esta es una ecuación matricial en B (BBT = C, siendo C dada), cuya solución puede encontrarse utilizando algunos conceptos del algebra matricial. Como C es el producto de una matriz por su transpuesta, entonces C debe ser simétrica y definida positivamente (o al menos semidefinida). De acuerdo a esta restricción sobre C, B puede encontrarse de la siguiente manera:

Donde P y R corresponden a los autovalores y autovectores de C, calculada como aparece en (4), respectivamente.
A manera de ejemplo considérense los siguientes 3 ríos: Nare, Grande y Magdalena. Sus aportes mensuales medidos en m3/s para el período 2002 – 2006 se ilustran en la Figura 2. En el caso del río Magdalena los datos se encuentran en una escala 1/10.
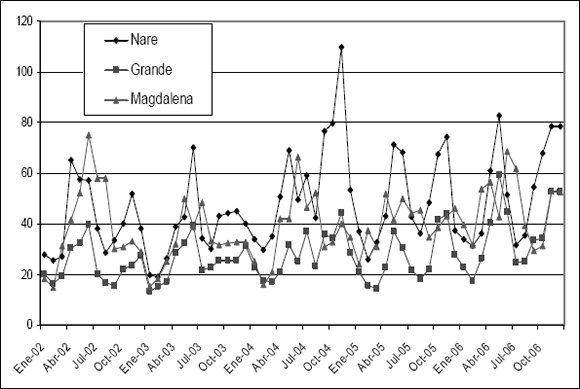
Figura 2. Histórico de los aportes mensuales de 3 ríos
Figure 2. History of 3 rivers monthly streamflows
El coeficiente de correlación entre estos ríos con datos del período 1963-2006 se muestra en la Tabla 1.
Tabla 1. Coeficiente de correlación
Table 1. Correlation coefficient
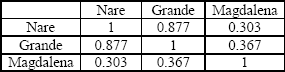
En esta tabla puede observarse que existe una marcada relación entre los caudales para un mes t de los ríos Nare y Grande, lo cual es fácilmente explicable dada su geografía, mientras que la relación con el río Magdalena es bastante baja.
En las Tablas 2 y 3 se muestran las correspondientes matrices Sxx y Syx, Emientras que en las Tablas 4 y 5 se muestran las matrices A y B resultantes.
Tabla 2. Matriz Sxx
Table 2. Sxx Matrix
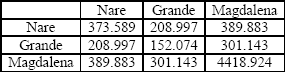
Tabla 3. Matriz Syx
Table 3. Syx Matrix
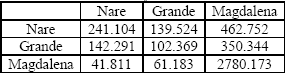
Tabla 4. Matriz A
Table 4. A Matrix
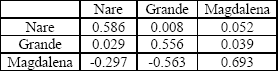
Tabla 5. Matriz B
Table 5. B Matrix
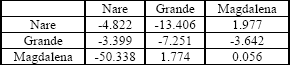
4. INCORPORACIÓN DE VARIABLE EXÓGENA Y DEFINICIÓN DE REGÍMENES
Una manera de mejorar el modelo descrito hasta este momento es incorporar una variable exógena que se encuentre altamente relacionada con las variables de interés, y de la cual se tenga disponible algún pronóstico o valor esperado. Para el caso del sistema hídrico Colombiano, la variable candidata es de carácter climático y se trata de la Temperatura Superficial del Mar (SST por sus siglas en inglés) para la zona Niño 3.4, de la cual diversas fuentes se pueden consultar para obtener pronósticos de mediano plazo (de uno a dos años hacia adelante) [1, 3, 5].
Para incorporar esta variable en el modelo se debe proceder como se describe a continuación.
Primero se realiza el preprocesamiento al pronóstico que se tenga de la SST según el procedimiento descrito en la siguiente sección.
Luego se generan trazas sintéticas de SST con el modelo de Thomas y Fiering, calculando previamente los σx y ρ respectivos. En el caso de los μx, estos corresponden a los valores esperados de acuerdo a algún pronóstico para el período en que este se encuentre disponible, y son iguales a cero de allí en adelante. Para este trabajo el pronóstico de SST utilizado fue el de la NOAA, el cual históricamente ha estado bastante acorde con las ocurrencias reales.
Los resultados de este modelo con información real hasta agosto de 2007 para 20 trazas se presentan en la Figura 3. Allí se observa que al menos hasta diciembre de 2007 se esperaban condiciones frías, lo cual es un factor común en las 20 series generadas, mientras que de ahí en adelante se presentan variadas posibles ocurrencias con una media cercana a cero.
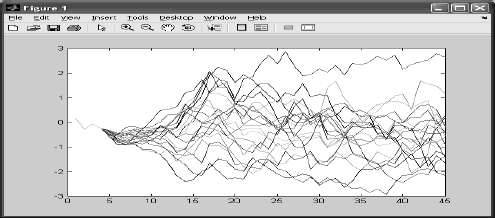
Figura 3. Generación de 20 trazas de SST
Figure 3. Generation of 20 SST traces
Una vez se obtienen las trazas de SST, éstas se utilizan para separar los datos de los caudales en regímenes o clases. Una manera de hacer esto es definir un rezago común para todos los caudales respecto al SST y utilizar un diagrama de frecuencia para separar los datos históricos de caudales en n regímenes con aproximadamente el mismo número de datos. En el caso de interés se contó con 528 datos tanto de caudales como de SST (con un rezago de 3 meses) y se emplearon 5 regímenes, de manera que cada uno contiene aproximadamente 105 datos. Los regímenes resultantes se separaron de la siguiente manera:
- R1: SST* <= -0.84
- R2: -0.84 < SST* <= -0.3162
- R3: -0.3162 < SST* <= 0.2397
- R4: 0.2397 < SST* <= 0.799
- R5: 0.799 < SST*
Donde SST* corresponde al valor del SST luego de aplicarle el preprocesamiento descrito en la siguiente sección.
Al separar los datos en n regímenes (en este caso el valor de n elegido es 5) se hace necesario considerar que (2) se convierte en n ecuaciones, una para cada régimen, por lo que es necesario calcular las matrices A y B en cada caso. Al hacer esto debe tenerse en cuenta que los estadísticos de interés como las matrices de covarianza entre los ríos con y sin rezago (Syx y Sxx) y por tanto los índices de correlación cruzada y de autocorrelación tienen que ser calculados para cada régimen bajo la premisa de que son significativamente diferentes en cada uno. Si esta condición no se cumple la división analizada no tendría justificación estadística.
5. PREPROCESAMIENTO DE LOS DATOS
Para garantizar el desempeño del modelo descrito en las secciones anteriores es importante anotar que los datos utilizados, tanto históricos como recientes, requieren de un preprocesamiento que facilita el desarrollo de los mismos. En este caso, tal como ya
se expuso, las variables consideradas son básicamente los caudales de los ríos que alimentan a las diferentes plantas de generación del país y la SST para la zona niño 3.4.
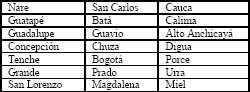
En el caso de los caudales se toma la serie histórica que se tenga disponible. En este caso se contó con la serie de los ríos que se muestran en la Tabla 6 (21 en total) desde 1963 hasta 2006.
Tabla 6. Caudales considerados
Table 6. Considered streamflows
Luego a dichos datos se les saca el logaritmo natural para garantizar que al generar las series sintéticas no se produzcan valores negativos de los caudales.
Posteriormente para cada uno de los doce meses se obtienen las medias y las desviaciones estándar, con las cuales se normalizan los datos resultantes. A manera de resumen se puede ver este proceso como:

Siendo Xm,a el dato de los caudales de los ríos en el mes m del año a.
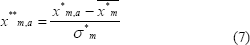
En el caso de la SST se procede de la misma manera para el mismo período de tiempo pero sin sacar el logaritmo natural de los datos (debido a que la estabilidad y rango de esta variable no lo justifican).
6. RESULTADOS
Los resultados obtenidos por el modelo se presentan en la Figura 4, donde pueden observarse una de las ocurrencias en valores normalizados para los 21 ríos analizados en un horizonte de 42 meses (de Agosto de 2007 a Diciembre de 2010).
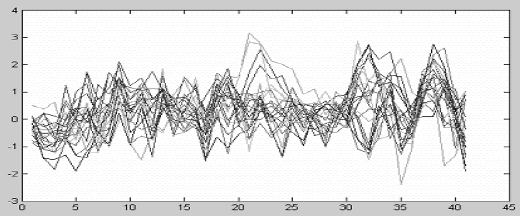
Figura 4. Generación de una traza de caudales (valores normalizados)
Figure 4. Generation of a flows traces (normalized values)
A pesar de que debido a la cantidad de ríos modelados en esta figura no se aprecie bien el comportamiento para cada uno en particular, si es posible notar el condicionamiento general a condiciones húmedas respecto a las medias para los primeros meses, mientras que de allí en adelante se presentan valores que oscilan alrededor del cero respetándose las correlaciones cruzadas y las autocorrelaciones, obteniéndose incluso valores pico, los cuales son de gran importancia en los análisis de riesgo en los que los agentes de los mercados eléctricos pueden estar interesados.
Igualmente a manera de resumen, y volviendo al ejemplo utilizado en la sección 3, en la Figura 5 se presenta una instancia de las series sintéticas obtenidas para los ríos Nare, Grande y Magdalena, así como los correspondientes valores de SST. En esta figura se observa que se preservan la magnitud de correlaciones entre los valores para los tres ríos, al tiempo que se observa su relación inversa con los valores correspondientes de SST.
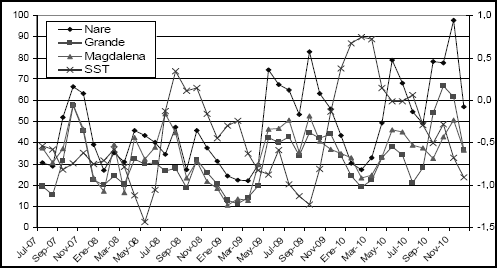
Figura 5. Generación de una traza de caudales (valores reales)
Figure 5. Generation of a streamflows traces (real values)
7. CONCLUSIONES
Si bien existen diversos modelos provenientes de la hidrología estocástica con los que es posible modelar series de caudales, el presentado en este artículo exhibe un enfoque novedoso en el sentido que incorpora una variable exógena como es la SST la cual condiciona las series sintéticas obtenidas sin dejar de preservar ciertos estadísticos de interés como las varianzas y covarianzas. Este aspecto es especialmente importante si dichas series son utilizadas para el pronóstico del precio de la electricidad en mercados con características como el Colombiano, en el que no solo las condiciones reales si no también la hidrología esperada, juega un papel fundamental en la determinación de dicho precio.
Por último cabe mencionar que otra ventaja del modelo propuesto es su robustez matemática la cual no representa necesariamente dificultades para su implementación gracias al uso de herramientas de programación como Matlab que permiten realizar operaciones matriciales con relativa facilidad.
REFERENCIAS
[1] CPC Climate Prediction Center. National Weather Service. Disponible: http://www.cpc.ncep.noaa.gov/ (citado 18 de Enero de 2008). [ Links ]
[2] CREG. Comisión de Regulación de Energía y Gas. Resolución 071. 2006 [ Links ]
[3] IRI. Internacional Research Institute for Climate and Society. Disponible: http://iri.columbia.edu/ (citado 18 de Enero de 2008) [ Links ]
[4] MATALAS, N. Mathematical assessment of synthetic hydrology, Water Resources Research 3 (4), pp. 937–945. 1967 [ Links ]
[5] NOAA. National Oceanic & Atmospheric Administration. United States department of commerce. Disponible: http://www.noaa.gov/ (citado 18 de Enero de 2008). [ Links ]
[6] THOMAS, H. & FIERING, M. Mathematical synthesis of streamflow sequences for the analysis of river basins by simulation. En: Maass A, Humfschmidt MM, Dorfman R, Thomas Jr HA, Marglin SA, Fair GM (eds) Design of water resource systems. Harvard University Press, Cambridge. 1962. [ Links ]
[7] UPME. Unidad de Planeación Minero Energética. República de Colombia, Ministerio de minas y energía. Disponible: http://www.upme.gov.co (citado 18 de Enero de 2008). [ Links ]
[8] VALENCIA, DARÍO. Optimización y simulación en sistemas de recursos hidráulicos. Universidad Nacional de Colombia. 1982. [ Links ]
[9] XM. Expertos en Mercados. Portal XM. Disponible: http://www.xm.com.co (citado 18 de Enero de 2008). [ Links ]
[10] YOUNG, G. & PISANO, W. Operational hydrology using residuals. Journal of Hydraulics Division, ASCE, 94(HY4): 909-923. 1968. [ Links ]














