Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.72 no.157 Medellín Jan./Apr. 2009
ANÁLISIS Y CONTROL DE UN BIORREACTOR ANAEROBIO DE LECHO FIJO DE FLUJO ASCENDENTE
ANALYSIS AND CONTROL OF AN ANAEROBIC UPFLOW FIXED BED BIOREACTOR
ALEJANDRO RINCON
Estudiante Doctorado en Ingeniería Línea de Investigación en Automática, Universidad Nacional de Colombia, sede Manizales
FABIOLA ANGULO GARCIA
Universidad Nacional de Colombia, Sede Manizales, fangulog@unal.edu.co
GERARD OLIVAR TOST
Departamento de Ingeniería Eléctrica, Electrónica y Computación, Universidad Nacional de Colombia, Sede Manizales
Recibido para revisar enero 23 de 2008, aceptado mayo 15 de 2008, versión final mayo 19 de 2008
RESUMEN: En este artículo se presenta el análisis dinámico y el diseño de un regulador autosintonizado para un biorreactor anaerobio de lecho fijo de flujo ascendente, utilizado para tratamiento de aguas residuales. Se ha demostrado de manera analítica que la condición de arrastre en el reactor se obtiene por una combinación de una bifurcación transcrítica con una del tipo silla-nodo. Una vez se determina el rango de operación del reactor se diseña un regulador autosintonizado para mejorar la remoción de materia orgánica, obteniéndose buenos resultados.
PALABRAS CLAVE: bifurcaciones, digestión anaerobia, regulador auto sintonizado.
ABSTRACT: this paper presents the bifurcation analysis in an anaerobic upflow fixed bed bioreactor, which is an anaerobic digestion system useful for wastewater treatment. In the dynamic analysis part, the equilibrium points, linear stability and bifurcation curves are studied, focusing in the washout condition. For the self tuning regulator the parameter estimation and control law are designed, and an integral action is introduced in order to address the disturbances. The simulation studies show the improvement of the performance when a disturbance appears.
KEY WORDS: bifurcation, anaerobic digestion, self tuning regulator.
1. INTRODUCCIÓN
Las normas ambientales propenden por limitar la cantidad de materia tóxica liberada por las industrias a través de sistemas de alcantarillado, a ríos. Esto ha provocado un creciente interés por la utilización de técnicas de control automático y optimización en plantas de tratamiento biológico de aguas residuales [1].
El objetivo de una planta de tratamiento de aguas residuales es disminuir la concentración de contaminantes orgánicos en la corriente de salida. Este objetivo puede ser cumplido manipulando la velocidad de dilución [2]. Desde los años 90 el modelado, análisis y control de procesos biotecnológicos, incluyendo los procesos de
digestión anaerobia y los procesos de tratamiento de aguas residuales en general, ha cobrado gran importancia, debido a la necesidad de cumplir las normativas ambientales. En [1,3,4] se han utilizado modelos a escala piloto, con el objeto de comprobar los resultados obtenidos teóricamente.
Existen diversos sistemas biológicos para el tratamiento de aguas residuales, que se clasifican en aerobios y anaerobios. Generalmente, los procesos anaerobios se usan para tratar residuos con alta carga orgánica contaminante, por ejemplo los lodos producidos por los tratamientos primarios y secundarios de las actividades económicas.
Una parte importante para obtener una buena remoción de materia orgánica en los procesos de digestión anaerobia, consiste en una adecuada selección del modelo. Existen diversas técnicas para obtener estos modelos. Ellos incluyen métodos que se basan en la fenomenología del proceso [4,5] y en el gradiente de concentraciones [4,6,7], principalmente.
Estos modelos pueden ser aplicados a diferentes tipos de procesos de tratamiento de aguas residuales: lodos activados, reactores de lecho fluidizado, reactores de lecho fijo, entre otros. Para propósitos de control lo más adecuado es utilizar modelos concentrados, que tengan en cuenta sólo una etapa, la metanogénesis, [8] o dos etapas, la acidogénica y la metanogénica [1,2,5]. En [9] se hace una revisión de los modelos dinámicos de varios tipos de biorreactores, en especial los utilizados para tratamiento de aguas residuales, teniendo en cuenta parámetros distribuidos y los fenómenos de transporte existentes.
En particular en este trabajo se analiza un proceso de digestión anaerobia, la cual consiste en un proceso microbiológico que se desarrolla en ausencia de oxígeno y comprende un conjunto de reacciones complejas. Estas reacciones están ligadas al metabolismo de numerosos microorganismos que actúan como intermediarios en la transformación de la materia orgánica hacia substratos directamente asimilables, que acaban convirtiéndose en biogás. Así pues la digestión anaerobia consiste en una descomposición de la materia orgánica, que genera como productos finales un gas de alto contenido energético, denominado biogás, y un lodo residual. De esta forma se presentan dos bondades en los sistemas de digestión anaerobia: la reducción de la carga orgánica y la producción de energía en forma de gas metano.
El biorreactor de lecho fijo de flujo ascendente anaerobio también recibe la denominación de bio-filtro anaerobio de flujo ascendente. Su principal ventaja radica en que ocupa poco espacio, lo que lo hace adecuado para industrias pequeñas. Consiste básicamente en una columna de relleno sobre la cual se desarrollan y fijan las bacterias anaeróbicas. El desarrollo de los microorganismos sobre un medio sólido hace que se logren tiempos de retención celular muy elevados con bajos tiempos de retención hidráulica.
La figura 1 muestra un diagrama esquemático del reactor. El agua a tratar pasa de abajo hacia arriba por el interior de la columna, donde los microorganismos realizan la depuración. Por la parte inferior entra el agua contaminada a tratar. En el interior de la columna están las bacterias que realizan la depuración. Por la parte superior se obtiene biogás y un efluente con menos carga orgánica, de esta forma se realiza la depuración. Hay una recirculación de microorganismos para evitar que gran cantidad de ellos salga a través del efluente. Esta recirculación generalmente no se tiene en cuenta en el modelado.
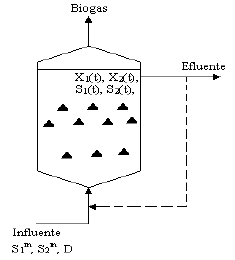
Figura 1. Esquema del proceso de digestión anaerobia
Figure 1. Scheme of anaerobic digestion process
En [2] se estudian los puntos de equilibrio, la condición de arrastre y el análisis de estabilidad para un sistema de digestión anaerobia y en [5,10] se desarrollan técnica de optimización para un sistema de este mismo tipo. Sin embargo, hasta ahora no se ha hecho un análisis exhaustivo de la dinámica del sistema, ya que en los trabajos previos, se analizan solo algunos puntos de equilibrio aislados, y en ningún momento se estudia su comportamiento, en la medida que cambian los parámetros en el sistema, lo cual es una suposición más realista.
El trabajo está organizado de la siguiente manera: en la sección 2 se presenta el modelo dinámico del sistema. En la sección 3 se hace un análisis de la estabilidad y de las bifurcaciones del sistema y se obtienen límites para la señal de control, de tal modo que se garantice la operación del reactor y no se llegue al arrastre de la biomasa. En la sección 4 se diseña y prueba un controlador adaptativo del tipo regulador autosintonizado y en la última sección se dan algunas conclusiones.
2. MODELO DEL SISTEMA
Se adoptó un modelo dinámico correspondiente a un biorreactor de lecho fijo de flujo ascendente, cuyas constantes fueron estimadas para una situación específica: un efluente de una destilería de vino cerca de Narbonne, Francia [1]. Las variables de estado del sistema son: X1(t) (concentración de biomasa acidogénica), X2(t) (concentración de biomasa metanogénica), S1(t) (concentración de la Demanda Química de Oxígeno DQO) y S2(t) (concentración de Ácidos Grasos Volátiles AGV. La variable independiente t representa el tiempo. Las leyes físicas y químicas que gobiernan las variables de estado están implícitas en balances de materia, que dan lugar a las siguientes ecuaciones diferenciales ordinarias:
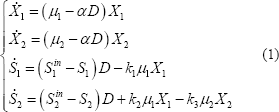
Donde:
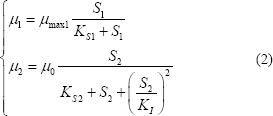
La variable D es la velocidad de dilución o factor de dilución, que se define como la razón entre el caudal de la corriente líquida que entra al biorreactor y el volumen ocupado por el líquido en el interior del biorreactor. Sus unidades son días-1 y en el presente trabajo tomará valores en el rango D Î [0 1.44] días-1.
S1 es la concentración de DQO (g/L).
S2 es la concentración de AGV (mmol/L).
X1 es la concentración de bacterias acidogénicas (g/L).
X2 es la concentración de bacterias metanogénicas (g/L).
S1in es la concentración de DQO en la corriente de entrada al biorreactor. S1in = 5.8 g/L.
S2in es la concentración de AGV en la corriente de entrada al biorreactor. S2in = 52 mmol/L.
α es la fracción de las bacterias en la fase líquida y refleja la heterogeneidad del proceso (adimensional). α = 0.5.
μ1 es la velocidad de crecimiento de la biomasa acidogénica (días-1).
μ2 es la velocidad de crecimiento de la biomasa metanogénica (días-1).
μmax1 es la velocidad de crecimiento máxima de la biomasa acidogénica (días-1). μmax1= 1.2días-1.
μ0 es el parámetro asociado con la velocidad de crecimiento máxima de la biomasa metanogénica (días-1). μ0=0.74días-1.
k1 es el coeficiente de rendimiento para la degradación de DQO (g DQO/g X1). k1=10.53g DQO/g X1.
k2 es el coeficiente de rendimiento para la producción de AGV (mmol AGV/g X1) k2=28.6 mmol AGV/g X1.
k3 es el coeficiente de rendimiento para el consumo de AGV (mmol AGV/g X2) k3=1074 mmol AGV/g X2.
KS1 es una constante de la cinética de Monod (g DQO/L). KS1=7.1 g DQO/L.
KS2 es una constante de la cinética de Haldane (mmol AGV/L). KS2=9.28 mmol AGV/L.
KI es una constante de la cinética de Haldane (mmol AGV/L)1/2 KI=16 (mmol AGV/L)1/2.
En la figura 1 se muestra el proceso de digestión anaerobia con las variables correspondientes.
3. ANÁLISIS DINÁMICO
En esta sección se hace un análisis dinámico del sistema descrito anteriormente. Se incluye un estudio de estabilidad y bifurcaciones.
El análisis de la condición de arrastre, en la cual ocurre la desaparición de la biomasa, es uno de los aspectos más importantes a tener en cuenta para el diseño de controladores de estos reactores. Una vez se obtiene el límite para el cual se da la condición de arrastre, se imponen restricciones a la señal de control o a los parámetros del mismo, con el fin de establecer condiciones que garanticen la operatividad del reactor en zona donde la biomasa se mantenga activa.
3.1 Puntos de equilibrio
El anterior sistema puede escribirse de manera compacta como 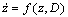 . Los puntos de equilibrio del sistema se encuentran haciendo
. Los puntos de equilibrio del sistema se encuentran haciendo 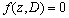 [11]. Sin embargo, teniendo en cuenta que no se ha asignado un valor al parámetro D, los puntos de equilibrio están en función de éste. Para determinar la estabilidad de los puntos de equilibrio se calcula el jacobiano del sistema, se evalúa en cada punto y se obtienen los valores propios. De acuerdo con esto, los valores propios estarán en función de D y así ése se presenta como un parámetro de bifurcación del sistema. Teniendo en cuenta que las variables del sistema sólo pueden tomar valores positivos, el espacio alcanzable está definido por la intersección de los subespacios X1>0, X2>0, S1>0 y S2>0. Para D menor que 1.07116 días-1 existen 2 nodos estables y cuatro sillas. Uno de los nodos es físicamente alcanzable, corresponde a X1>0, X2>0, S1>0, S2>0 y es llamado primer equilibrio. El otro nodo es físicamente no alcanzable, se nota como sexto equilibrio, y corresponde a X1>0, X2<0, S1>0, S2>0. De las cuatro sillas, una está en el subespacio no alcanzable y las otras 3 están en el espacio físicamente alcanzable. Las sillas alcanzables presentan las siguientes características: una corresponde con X1=0, X2=0, S1>0, S2>0; otra corresponde a X1=0, X2>0, S1>0, S2>0, y la tercera corresponde a X1>0, X2=0, S1>0, S2> 0. A esta última silla se le nota como quinto punto de equilibrio en las gráficas. Para valores de D en el intervalo 1.07116 a 1.071851 días-1 existen 2 nodos estables, ambos físicamente alcanzables. Uno corresponde a la condición de arrastre (washout) y el otro a la operación normal del reactor. Para valores de D>1.071851días-1, se presenta un único punto de equilibrio estable correspondiente a la condición de arrastre del sistema (X2=0).
[11]. Sin embargo, teniendo en cuenta que no se ha asignado un valor al parámetro D, los puntos de equilibrio están en función de éste. Para determinar la estabilidad de los puntos de equilibrio se calcula el jacobiano del sistema, se evalúa en cada punto y se obtienen los valores propios. De acuerdo con esto, los valores propios estarán en función de D y así ése se presenta como un parámetro de bifurcación del sistema. Teniendo en cuenta que las variables del sistema sólo pueden tomar valores positivos, el espacio alcanzable está definido por la intersección de los subespacios X1>0, X2>0, S1>0 y S2>0. Para D menor que 1.07116 días-1 existen 2 nodos estables y cuatro sillas. Uno de los nodos es físicamente alcanzable, corresponde a X1>0, X2>0, S1>0, S2>0 y es llamado primer equilibrio. El otro nodo es físicamente no alcanzable, se nota como sexto equilibrio, y corresponde a X1>0, X2<0, S1>0, S2>0. De las cuatro sillas, una está en el subespacio no alcanzable y las otras 3 están en el espacio físicamente alcanzable. Las sillas alcanzables presentan las siguientes características: una corresponde con X1=0, X2=0, S1>0, S2>0; otra corresponde a X1=0, X2>0, S1>0, S2>0, y la tercera corresponde a X1>0, X2=0, S1>0, S2> 0. A esta última silla se le nota como quinto punto de equilibrio en las gráficas. Para valores de D en el intervalo 1.07116 a 1.071851 días-1 existen 2 nodos estables, ambos físicamente alcanzables. Uno corresponde a la condición de arrastre (washout) y el otro a la operación normal del reactor. Para valores de D>1.071851días-1, se presenta un único punto de equilibrio estable correspondiente a la condición de arrastre del sistema (X2=0).
3.2 Análisis de los puntos de equilibrio, usando la variable X2
El diagrama de bifurcaciones muestra una parábola que está definida sólo para D≤1.071851días-1. El estudio de la estabilidad se obtuvo con base en el análisis de los valores propios, que se muestran en la figura 3 y completado con los diagramas de bifurcaciones. En la figura 3 se puede ver la evolución de los puntos de equilibrio en una región amplia del espacio de parámetros y en la figura 4 se presenta un zoom de las curvas de bifurcación y las características de estabilidad correspondientes. Se utiliza la convención de una línea continua gruesa para equilibrios estables y línea a trozos para equilibrios inestables. Las figuras 3 y 4 se obtuvieron con base en las expresiones analíticas de los puntos de equilibrio. Utilizando el software MATCONT, basado en métodos de continuación, se estudió el sistema encontrando idénticos resultados.
En la figura 2 se observa que un punto de equilibrio (notado como sexto equilibrio en la figura) cruza dos veces por cero: la primera para un valor de D=1.07116 y la segunda para un valor de D=1.071851.
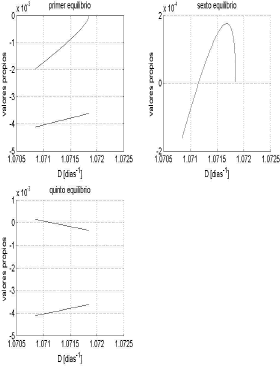
Figura 2. Comportamiento de los valores propios más relevantes para las bifurcaciones transcrítica y fold
Figure 2. Behaviour of the main eigenvalues for transcritical and fold bifurcations
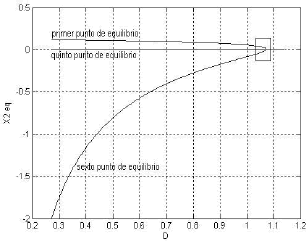
Figura 3. Curvas de equilibrio
Figure 3. Equilibrium curves
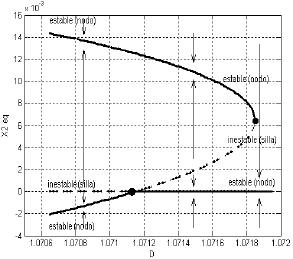
Figura 4. Bifurcaciones transcrítica y nodo-silla
Figure 4. Transcritical and node-saddle bifurcations
La figura 3 muestra el comportamiento de estos mismo equilibrios en una amplia zona del espacio de variación del parámetro D. El primer punto de equilibrio corresponde con un nodo estable alcanzable para todo D<1.071851. El sexto punto de equilibrio corresponde a un nodo estable no alcanzable físicamente para D<1.07116. El quinto punto de equilibrio corresponde a una silla para D<1.07116 y a un nodo estable alcanzable para 1.07116<D<1.071851
A continuación se presenta un análisis más detallado del comportamiento y evolución de estos puntos de equilibrio, en la medida que se varía el parámetro D.
3.2.1 Bifurcación transcrítica
En la figura 4 se puede ver que para D<1.07116 sólo existe un punto de equilibrio estable, alcanzable, en el sistema, correspondiente a un nodo. Sin embargo coexisten, como ya se dijo, cuatro sillas y otro nodo estable no alcanzable. En D=1.07116 días-1 el nodo estable inalcanzable colisiona con una silla definida para X2eq=0. A partir de este momento se cambian las características de estabilidad. Así se transfiere la característica de nodo estable al equilibrio generado con X2eq=0 (con D>1.07116 dias-1) y la rama que continúa hacia el punto X2=0.00631368 g/L corresponde a una silla. Se reconoce como una bifurcación transcrítica pues se intersectan dos ramas con tangentes distintas, de forma que cada rama aparece a ambos lados del punto de bifurcación. Esto se puede observar en la figura 4.
Haciendo un análisis de los valores propios a medida que se varía el parámetro D se tiene que para D<1.07116 dias-1 los valores propios del nodo son reales y negativos, y los de la silla, tres son reales negativos y uno real positivo. Al llegar a D=1.07116 dias-1 el valor propio positivo de la silla se hace cero (Figura 2, quinto equilibrio) y uno de los valores propios negativos del nodo inalcanzable se hace cero (Figura 2, sexto equilibrio). Si se continúa aumentando el parámetro, se tiene que el valor propio que provenía del nodo estable y pasó por cero, se hace ahora positivo, con lo cual adquiere el carácter de silla (Figura 2 sexto equilibrio). Por el contrario el valor propio de la silla que pasó por cero, continúa decreciendo, y hace que la silla se vuelve un nodo estable (Figura 2, quinto equilibrio). Se observa que el carácter de los valores propios asociados al primer equilibrio no cambia (ambos son negativos para todo el rango de D considerado).
3.2.2 Bifurcación nodo-silla
A partir de D=1.07116 dias-1 la rama que continúa hacia el punto X2=0.00631368 g/L corresponde a una silla. En D=1.071851, esta silla, y el nodo que proviene del espacio alcanzable, se unen en un sólo punto. El punto donde se aniquilan los dos equilibrios (D=1.071851, X2=0.00631368) es un nodo-silla, ya que corresponde a la fusión de un nodo y una silla. De esta forma, el nodo-silla está separando un equilibrio estable (nodo) de uno inestable (silla). Este fenómeno se puede observar en la figura 4.
Haciendo un análisis de los valores propios, similar al anterior, se observa que a medida que se varía el parámetro D, para D>1.07116 dias-1, se tienen los siguientes resultados: si D<1.071851 los valores propios de los dos nodos (ambos alcanzables) son reales y negativos, y los de la silla tres son reales negativos y uno real positivo. Al llegar a D=1.071851 dias-1 el valor propio positivo de la silla se hace cero (Figura 2, sexto equilibrio) y uno de los valores propios negativos de uno de los nodos alcanzables (correspondiente al punto e operación del sistema) se hace cero (Figura 2, primer equilibrio). Si se continúa aumentando el parámetro, se tiene que el único equilibrio del sistema corresponde con el nodo estable de la condición de arrastre (X2=0).
En la bifurcación nodo-silla ocurre el arrastre, es decir, hay desaparición de una biomasa, la biomasa metanogénica. Para los sistemas de digestión anaerobia se busca siempre evitar llegar a este punto, dado que si desaparece la biomasa metanogénica se deja de producir metano, que es un combustible valioso, y no se realiza degradación de la DQO.
Así pues el rango en el cual D debe estar y que garantiza la correcta operación del sistema es D<1.07116. Si bien para 1.07116<D<1.071851 se presenta un nodo estable operacional, es posible que perturbaciones en el sistema lo lleven al otro equilibrio alcanzable también, y que corresponde con la condición de arrastre.
Debe anotarse acá, que en esta sección se ha hecho un análisis dinámico del sistema, el cual no solo ha hecho uso del concepto de linealización, sino que por el contrario ha tratado la dinámica no lineal del sistema en conjunto. Una vez se dispone del análisis dinámico del reactor, se procede al diseño del controlador. En este sentido, los resultados obtenidos permiten establecer las condiciones para las cuales se da la condición de arrastre. Con esta idea en mente se procede a calcular un controlador adaptativo con modelo de referencia que evite que el sistema alcance la condición de arrastre.
4. ESTRATEGIA DE CONTROL
La variable controlada es la concentración de la DQO en la corriente de salida del biorreactor (S1). La variable de control (entrada de control) es la velocidad de dilución (D), la cual se regula por medio de una válvula. Se quiere que la salida siga una señal de referencia especificada a través de un modelo referencia [2,12] aún en presencia de perturbaciones. La perturbación considerada consiste en un cambio en la DQO en la corriente de entrada, simbolizada por S1in.
Se diseñará un control adaptativo del tipo regulador autosintonizado, con base en los procedimientos estándar establecidos en [13]. Se requiere una primera parte de estimación de parámetros de la planta, y una segunda parte de cálculo de los parámetros del controlador y de la entrada de control. Los parámetros del controlador se calculan con base en los estimados de los parámetros de la planta, y suponen que estos estimados son coherentes con la realidad, correspondiendo con el principio de equivalencia certera.
Se asume que el proceso se comporta como una planta de primer o segundo u otro orden, donde los parámetros varían lentamente en el tiempo y son estimados mediante algún mecanismo. Esta suposición es válida ya que los procesos de digestión anaerobia son bastante lentos. Para verificar este supuesto se realizaron varias perturbaciones en la entrada de control. En la figura 5 se presentan las gráficas de la respuesta del sistema y la entrada. Como se puede ver, la salida responde como si fuera una planta de primer orden.
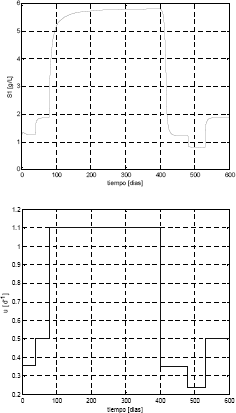
Figura 5. Respuesta del sistema ante el escalón
Figure 5. Step response of the system
4.1 Estimación de parámetros
Para la estimación de parámetros se utilizaron mínimos cuadrados recursivos, Este método se basa en los datos de la salida y la entrada para estimar los parámetros variantes en el tiempo [13]. Tal como se dijo antes se supone que la planta tiene el siguiente comportamiento:
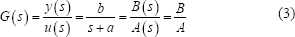
Esta función puede ser expresada como:

Supóngase ahora que se aplica un filtro de la siguiente forma:

El filtro está dado por la siguiente expresión:

Se define el operador 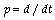 . Si se aplica el filtro anterior al modelo, éste puede escribirse como:
. Si se aplica el filtro anterior al modelo, éste puede escribirse como: 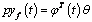 donde
donde

El método de mínimos cuadrados con olvido exponencial, aplicado a la planta de primer orden, (n=1), está dado por las siguientes ecuaciones:
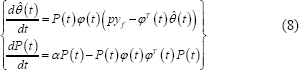
Donde a es el factor de olvido. Este algoritmo proporciona los estimados de los parámetros de la planta, que son usados para el cálculo de los parámetros de la ley de control. Así pues

4.2 Diseño del controlador
Para el diseño del controlador se utiliza ubicación de polos de grado mínimo, de acuerdo al procedimiento de [13]. Los polos del sistema en lazo cerrado deben corresponder a los polos deseados y así la salida del sistema sigue a la referencia. El diagrama general se presenta en la figura 6.
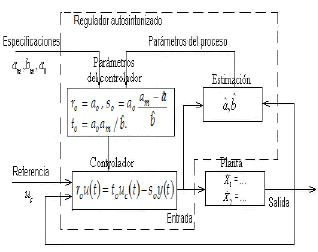
Figura 6. Diagrama del sistema estimador-controlador
Figure 6. Schematic diagram of estimator-controller
Se considera un controlador lineal de la forma:

Donde 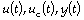 son la entrada de control, la referencia y la salida, respectivamente.
son la entrada de control, la referencia y la salida, respectivamente. 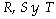 son los polinomios del controlador, los cuales deben ser calculados. La salida deseada o señal de referencia está dada por el modelo de referencia, llamado también función de transferencia en lazo cerrado deseada, la cual para este caso particular, y teniendo en cuenta que se asume que el sistema se comporta como un sistema de primer orden, debe ser de orden uno. Puede ser expresada como:
son los polinomios del controlador, los cuales deben ser calculados. La salida deseada o señal de referencia está dada por el modelo de referencia, llamado también función de transferencia en lazo cerrado deseada, la cual para este caso particular, y teniendo en cuenta que se asume que el sistema se comporta como un sistema de primer orden, debe ser de orden uno. Puede ser expresada como:
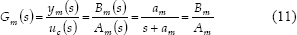
Donde 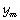 y
y 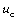 son la salida deseada y la referencia. Con el fin de que la salida del sistema siga la señal de referencia, la función de transferencia en lazo cerrado se iguala a la función de transferencia del modelo de referencia:
son la salida deseada y la referencia. Con el fin de que la salida del sistema siga la señal de referencia, la función de transferencia en lazo cerrado se iguala a la función de transferencia del modelo de referencia:

Donde 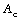 es el polinomio característico en lazo cerrado deseado. Se asume que hay cancelación de factores de BT y Ac, lo cual implica, en primer lugar, la factorización del polinomio B:
es el polinomio característico en lazo cerrado deseado. Se asume que hay cancelación de factores de BT y Ac, lo cual implica, en primer lugar, la factorización del polinomio B: 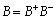 , donde
, donde 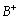 es un polinomio mónico, cuyos ceros son estables y bien amortiguados. En segundo lugar, la factorización de
es un polinomio mónico, cuyos ceros son estables y bien amortiguados. En segundo lugar, la factorización de 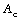 , de acuerdo con la ecuación Diofantina:
, de acuerdo con la ecuación Diofantina:
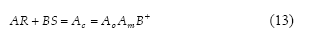
Donde 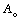 es el polinomio observador. Las condiciones de causalidad permiten determinar el grado de los polinomios del controlador, y las ecuaciones (12) y (13) los coeficientes correspondientes.
es el polinomio observador. Las condiciones de causalidad permiten determinar el grado de los polinomios del controlador, y las ecuaciones (12) y (13) los coeficientes correspondientes.
Al aplicar el procedimiento descrito al sistema en estudio, el primer paso es factorizar el polinomio B, obteniéndose: 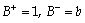 . Las condiciones de causalidad indican los grados de los polinomios:
. Las condiciones de causalidad indican los grados de los polinomios:
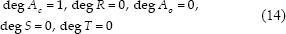
lo cual implica que los polinomios son términos constantes:
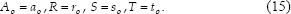
La ecuación Diofantina (13) permite determinar los coeficientes 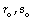 , y las ecuaciones (12) y (13) el coeficiente
, y las ecuaciones (12) y (13) el coeficiente 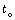 :
:
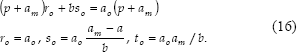
La ley de de control se obtiene entonces reemplazando los coeficientes de (15) y (16) en (10), teniendo en cuenta que los parámetros de la planta se conocen por estimación de acuerdo con (9):
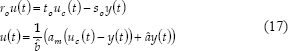
4.3 Simulación
Al simular el controlador aplicando una perturbación en el parámetro S1in que pasa de 5.8 a 10 g/L en el momento 100 días, se obtienen los resultados que se muestran en la figura 7. Se observa que el controlador rechaza las perturbaciones adecuadamente y sigue el modelo de referencia. Las oscilaciones que se presentan en el transitorio del sistema se deben al algoritmo de estimación de parámetros.
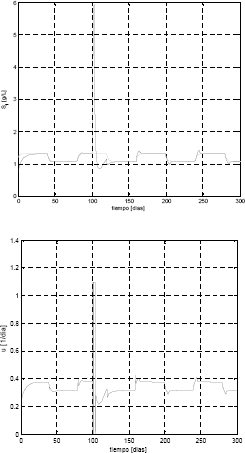
Figura 7. Comportamiento del sistema y esfuerzo de control ante perturbaciones
Figure 7. Behaviour of the system and control effort in presence of disturbances
5. CONCLUSIONES
En este trabajo se observa claramente el efecto de las no linealidades, las cuales no pueden ser consideradas en un modelo lineal. Si bien la dinámica del proceso de digestión anaerobia puede ser aproximada por un sistema de primer orden, es claro que la variable de control D no puede tomar valores por fuera de determinado rango. Así pues este tipo de análisis se convierte en una herramienta útil al momento de diseñar controladores. Se ha demostrado de manera analítica que la condición de arrastre se obtiene por una bifurcación transcrítica.
El washout o arrastre del proceso corresponde con una bifurcación del sistema y puede ser evitado imponiendo una saturación a la velocidad de dilución D.
Se diseñó y probó un controlador adaptativo, del tipo regulador autosintonizado, para controlar la DQO teniendo en cuenta la restricción de saturación en la señal de control, de tal manera que no sea posible llegar al fenómeno del arrastre. La planta se pudo aproximar como un sistema de primer orden para estimar los parámetros. Este controlador rechaza perturbaciones generadas en la concentración de la DQO en la corriente de entrada, tal como se observa en la figura 7.
Aunque el punto de operación es estable en el rango 1.07116<D<1.071851, se debe tener cuidado con la señal de control, pues si se permite que tome valores en este rango, es posible que ante alguna perturbación el sistema llegue a la condición de arrastre. Así pues D debe saturarse a D=1.07116.
REFERENCIAS
[1] BERNARD O., HADJ-SADOK Z., DOCHAIN D., GENOVESI A. AND STEYER J.P. Dynamical model development and parameter identification for an anaerobic wastewater treatment process, Biotechnology and Bioengineering, 75, 424-438, 2001. [ Links ]
[2] MÉNDEZ-ACOSTA H.O., CAMPOS-DELGADO D.U., FEMAT R. AND GONZÁLES-ALVAREZ V. A robust feedforward/feedback control for an anaerobic digester, Computers and Chemical Engineering, 29, 1613-1623, 2005. [ Links ]
[3] HILGERT N., HARMAND J., STEYER J.P. AND VILA J.P. Nonparametric identification and adaptative control of an anaerobic fluidized bed digester, Control Engineering Practice, 8, 367-376, 2000. [ Links ]
[4] BETEAU J.F., OTTON V., HILN J.Y., DELPECH F. AND CHERUY A. Modelling of anaerobic digestion in a fluidised bed with a view to control, Biochemical Engineering Journal, 24, 255-267, 2005. [ Links ]
[5] SIMEONOV I. AND QUEINNEC I. Linearizing control of the anaerobic digestion with addition of acetate (control of the anaerobic digestion), Control Engineering Practice, 14, 799-810, 2006. [ Links ]
[6] BOURREL S., DOCHAIN D., BABARY J.P. AND QUEINNEC I. Modelling, identification and control of a denitrifying biofilter, Journal of Process Control, 10, 73-91, 2000. [ Links ]
[7] BABARY J.P., JULIEN S., NIHTILA M.T., CZECZOT J. AND METZGER. New boundary conditions and adaptative control of fixed-bed bioreactors, Chemical Engineering and Processing, 38, 35-44, 1999. [ Links ]
[8] MARCOS N.I., GUAY M., DOCHAIN D., AND ZHANG T. Adaptive extremum seeking control of a continuous stirred tank bioreactor with Haldanes Kinetics, Journal of Process Control, 14, 317-328, 2004. [ Links ]
[9] SARAVANAN V. AND SREEKRISHNAN T.R.. Modelling anaerobic biofilm reactors – a review, Journal of Environmental Management, 81, 1-18, 2006. [ Links ]
[10] GUAY M., DOCHAIN D. AND PERRIER M. Adaptive extremum seeking control of continuous stirred tank bioreactors with unknown growth kinetics, Automatica, 40, 881-888, 2004. [ Links ]
[11] KUZNETSOV, Y.A., Elements of applied bifurcation theory, Springer Verlag, New York, 1995. [ Links ]
[12] ESTABEN M., POLIT M. AND STEYER J.P. Fuzzy control for an anaerobic digester, Control Engineering Practice, 5, 1303-1310, 1997. [ Links ]
[13] ASTROM K. AND WITTENMARK B., Adaptive control, Addison-Wesley Publishing Company, Reading MA, 1995. [ Links ]














