Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.72 no.157 Medellín Jan./Apr. 2009
MODELADO MATEMÁTICO DEL COMPORTAMIENTO MECÁNICO DE UN FRAGMENTO DE CARTÍLAGO ARTICULAR
MATHEMATICAL MODELING OF THE MECHANICAL BEHAVIOR OF AN ARTICULAR CARTILAGE PIECE
NANCY STELLA LANDÍNEZ
Profesor Asistente, Universidad Nacional de Colombia, Facultad de Medicina, nslandinezp@unal.edu.co
JUAN CARLOS VANEGAS
Universidad Nacional de Colombia, Facultad de Medicina, jcvanegasa@unal.edu.co
DIEGO ALEXANDER GARZÓN
Profesor Asociado, Universidad Nacional de Colombia, Facultad de Ingeniería, dagarzona@unal.edu.co
Recibido para revisar febrero 20 de 2008, aceptado agosto 28 de 2008, versión final septiembre 12 de 2008
RESUMEN: El cartílago articular es un material biológico poroelástico que permite la distribución de las cargas mecánicas y el movimiento de las articulaciones. Como material bifásico, en presencia de carga, el cartílago articular deforma su matriz sólida y modifica la presión hidrostática del fluido en su interior. El objetivo del presente trabajo es implementar numéricamente un modelo matemático que predice el comportamiento mecánico del cartílago articular teniendo en cuenta la dualidad entre la matriz sólida y el líquido articular, y la característica de poroelasticidad. Utilizando una metodología basada en el método de los elementos finitos, se simuló el comportamiento de un fragmento de cartílago articular en una y dos dimensiones, ante cargas mecánicas de tensión, compresión y oscilación. El análisis de los resultados permite validar cualitativamente el comportamiento poroelástico del modelo debido a la deformación de la matriz sólida y a la salida de fluido que modifica la presión del mismo de manera similar a lo reportado en trabajos experimentales. Se concluye que el modelo matemático permite realizar predicciones sobre el comportamiento biomecánico del cartílago articular, contribuyendo al proceso investigativo en áreas como la biomecánica y la ingeniería de tejidos.
PALABRAS CLAVE: Cartílago Articular, Modelado Matemático, Poroelasticidad, Elementos Finitos.
ABSTRACT: The articular cartilage is a poroelastic biological material that allows the distribution of mechanical loads and the joint movements. As a biphasic material, in presence of load, the articular cartilage deforms its solid matrix and modifies the fluid hydrostatic pressure inside. The aim of this work is to implement numerically a mathematical model that predicts the mechanical behaviour of articular cartilage taking into account the duality between the solid matrix and articular liquid, and its poroelastic feature. Using a finite element method approach , the response of a piece of articular cartilage in one and two dimensions has been simulated, with tensile, compresive and oscillative mechanical loads. The analysis of results allows a qualitatively validation of the poroelastic behavior of the model due to the solid matrix deformation and the fluid outflow that causes variations of pressures inside the articular cartilage according with reported trials. We conclude that the mathematical model allows the prediction of the articular cartilage biomechanical behaviour. Our results contribute to the investigative processes in fields of study like biomechanics and tissue engineering.
KEYWORDS: Articular cartilage, poroelasticity, mathematical model, Finite Elements.
1. INTRODUCCIÓN
La osteoartrosis (OA) es una entidad patológica originada por el deterioro del cartílago de las articulaciones sinoviales que compromete a un número creciente de personas en todo el mundo y afecta su calidad de vida [1-2]. La OA compromete la función músculo esquelética causando dolor y dificultad para desarrollar las actividades cotidianas. Diversos estudios han demostrado que las fuerzas ejercidas sobre el cartílago articular modifican la estructura y composición del tejido y generan cambios en su comportamiento biomecánico [3]. El inicio y la progresión de la osteoartrosis están comúnmente afectados por factores mecánicos relacionados bien sea con la carga articular o con la tensión por el contacto local [4].
Los materiales biológicos son en general multifásicos, coexistiendo una fase sólida y otra fluida [5-8]. Poseen además una marcada micro estructura que proporciona el carácter heterogéneo y anisótropo y, adicionalmente, posee un comportamiento mecánico fuertemente no lineal [6], [9-11]. La teoría general bifásica toma su forma más simple bajo tensiones pequeñas y con un coeficiente de permeabilidad constante. Estos postulados constituyen el cuerpo de lo que es conocido como la teoría lineal bifásica para el cartílago. Bajo condiciones estrictas de laboratorio, esta teoría lineal bifásica permite una descripción bastante exacta de los comportamientos de creep compresivo y de tensión-relajación de este tejido [7]. Sin embargo estos simples postulados no son válidos para describir la anisotropía del cartílago articular. Si el material se somete a grandes cargas o deformaciones, o a aplicaciones de cargas rápidas, se producen efectos de deformación no lineales cuya descripción requiere de teorías más avanzadas [12].
De acuerdo a esto, el cartílago articular corresponde a los tejidos blandos denominados hidratados, los cuales tienen un comportamiento altamente compresible correspondiente a un material bifásico saturado con la posibilidad de evacuación del fluido [13-15]. Varios autores han realizado sus investigaciones creando modelos del cartílago a partir de este comportamiento bifásico [7-8], [16-22], lo que permite analizarlo como un material con comportamiento poroelástico en respuesta a las cargas. Para solucionar estos modelos, el análisis computacional por elementos finitos ha sido usado como acercamiento a diversos procesos biológicos entre ellos el comportamiento biomecánico del cartílago articular [9-11], [17], [21-25]. La simulación de este comportamiento evolutivo permite entonces establecer predicciones sobre procesos cuya evaluación experimental es muy costosa y a veces imposible.
El objetivo del presente trabajo es implementar un modelo matemático con base en el método de los elementos finitos, para predecir el comportamiento mecánico del cartílago articular considerándolo como un material poroelástico. Se inicia con una revisión mecanobiológica del cartílago articular, seguida por el planteamiento del comportamiento matemático del tejido que permite plantear un modelo computacional mediante la utilización de los elementos finitos. Finalmente se presentan los resultados obtenidos a partir de la implementación del modelo en una y dos dimensiones, se realiza la discusión de los resultados y se señalan las líneas de trabajo futuro.
2. EL CARTILAGO ARTICULAR
El cartílago articular recubre la mayoría de las articulaciones diartrósicas de los seres humanos. Corresponde al cartílago hialino y es un componente muy especializado que facilita los movimientos articulares, resistiendo las cargas que se pueden experimentar durante los movimientos. A nivel de las articulaciones, el cartílago debe cumplir con dos funciones esenciales, (1) distribuir cargas articulares sobre un área amplia, disminuyendo así las solicitaciones mantenidas por el contacto de las superficies articulares [26]; y (2) permitir el movimiento relativo con mínima fricción y desgaste entre las superficies articulares opuestas [27]. El espesor de este tipo de cartílago en una persona adulta se relaciona con la ubicación del mismo; por ejemplo, a nivel de la rodilla, una de las más grandes articulaciones del cuerpo, el espesor puede ser de 3 a 4 mm, mientras que en una articulación interfalángica de la mano puede ser de 1 a 2 mm [12].
Clásicamente el cartílago ha sido considerado como un tejido avascular, aneural y alinfático, compuesto por células denominadas condrocitos, rodeadas por una matriz extracelular (MEC) que ellos mismos secretan [12],[28]. Dentro de la MEC los condrocitos se ubican en espacios llamados lagunas (Figura 1). Los condrocitos sintetizan y secretan los componentes orgánicos de la MEC que son básicamente colágeno, ácido hialurónico, proteoglicanos (PGs) y glicoproteínas [28-30].
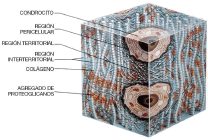
Figura 1. Estructura del Cartílago Articular. Adaptado de [32]
Figure 1. Articular Cartilage Structure. Adapted from [32]
2.1 Mecánica del Cartílago Articular (CA)
Las propiedades mecánicas del cartílago articular (CA) se atribuyen a su estructura compleja y a la composición de la MEC que comprende una fase de fluido (agua con iones disueltos), y una matriz sólida (colágeno tipo II, agregados de PGs, proteínas, lípidos, y células) [17]. Con la carga mecánica, el fluido intersticial se redistribuye a través de los poros de la matriz sólida permeable, dando lugar a una conducta predominantemente poroelástica. Este comportamiento del CA, se debe principalmente a dos mecanismos: (a) la fuerza de fricción debida al arrastre del flujo de líquido intersticial a través de la matriz sólida porosa (mecanismo dependiente del flujo), y (b) la deformabilidad de la matriz sólida en función del tiempo (mecanismo flujo-independiente) [31].
3. MATERIALES Y METODOS
Varios autores, [7-8],[16-22] han realizado sus investigaciones sobre cartílago a partir del comportamiento bifásico que exhibe este tejido. Esto ha permitido realizar un análisis del mismo como un material con un comportamiento poroelástico capaz de soportar cargas. El modelo matemático del CA como material bifásico, analiza el desplazamiento u(t,x) del sólido (matriz) y la presión p(x) del fluido que es desplazado por la carga, gracias a su característica de poroelasticidad. Este modelo es descrito por las ecuaciones (1) y (2):
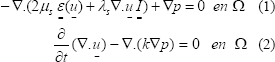
La ecuación (1) se deriva de la ley de conservación de momento y corresponde con la ecuación de elasticidad lineal (término 1a) acoplada con un término que representa la presión del fluido (término 1b). El término corresponde al tensor de deformación que actúa sobre la superficie G encerrada por W . son las constantes elásticas de Lamé para el sólido, relacionadas con el módulo de Young y el coeficiente de Poisson (E, ν). Por su parte, la ecuación (2) hace referencia al cambio de la dilatación de la matriz sólida (término 2a) ante la carga mecánica creada por la divergencia del gradiente de la presión del fluido contenido en el dominio W (término 2b) [5]. En esta ecuación, es una constante que representa el modulo de permeabilidad del sólido.
Las condiciones de contorno del modelo son definidas en el dominio G y pueden ser dependientes en el tiempo. La expresión matemática de estas condiciones es (3-6):
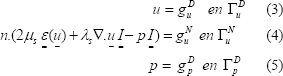
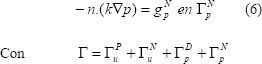
Un método extensamente utilizado para la solución de ecuaciones diferenciales parciales en geometrías complejas es el método de los elementos finitos [33]. Este método permite implementar numéricamente el modelo presentado en las ecuaciones (1) y (2) de manera simple y con un bajo consto computacional. El método consiste en utilizar una función vectorial W o función de ponderación y una función escalar q, encargadas de minimizar los términos de las ecuaciones (1) y (2). Multiplicando (1) por W y (2) por q, y realizando integración por partes en el dominio , se obtiene un variacional de la forma [5]:
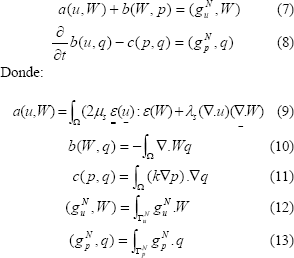
El método de solución se basa en dividir el dominio W (medio continuo) sobre el que están definidas las ecuaciones (1) y (2) en su forma integral en una serie de subdominios no intersectantes We denominados elementos finitos. El conjunto de elementos finitos forma una partición del dominio denominada discretización que en conjunto se describe a partir de las ecuaciones (14) y (15):
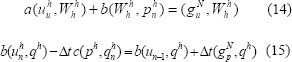
En (15) el subíndice indica el valor de un parámetro en un tiempo , mientras que el subíndice indica el valor en el tiempo siguiente . [5]. Usando el método de Galerkin, las funciones W y q se aproximan por la expresión matricial (16) donde el vector N contiene las funciones de forma normalizadas (x,h) que permiten realizar la interpolación al interior de cada elemento del dominio.
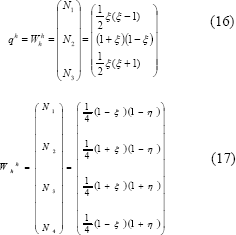
En (16), las funciones de forma corresponden al caso de elementos unidimensionales de tres nodos (figura 2a). Para el caso bidimensional, se utilizan elementos de cuatro nodos cuyas funciones de forma normalizadas son las mostradas en la forma matricial (17) y en la figura 2b.
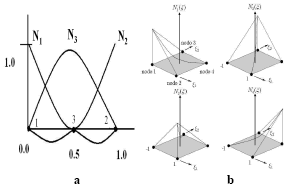
Figura 2. Representación de las funciones de forma. a) Caso 1D, 3 nodos por elemento. b) Caso 2D, elementos con cuatro nodos [35]
Figure 2. Form functions representation . a) Case 1D, three-nodal elements. b) Case 2D, four-nodal elements [35]
Si se cambia el espacio de integración de (x,y) a (x,h) mediante el jacobiano de la transformación y se ajusta la notación vectorial, las ecuaciones (1) y (2) pueden reducirse a un sistema matricial de tipo elemental de la forma (18) que corresponde a la discretización algebráica en el dominio We de un elemento, con k la matriz de rigidez elemental, m las incógnitas y f el término independiente. Ensamblando el resultado de (18) para el total de elementos en W se obtiene un sistema matricial general definido como (19) donde K es la matriz global de rigidez, M el vector de incógnitas y F el vector global de entradas.
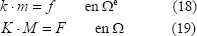
3.1 Implementación
La solución de estas ecuaciones tanto para u como para p se implementó usando una rutina de usuario programada en Fortran y un PC de escritorio con procesador AMD de 2.4 GHz y 1.0 GB de memoria RAM.
3.1.1 Simulación
Las condiciones para la simulación se basaron en los experimentos realizados por Frijns [5] y Wu [37]. Se realizaron simulaciones para 1D y 2D, buscando respuesta del tejido ante la aplicación de cargas de (a) compresión, (b) tensión y (c) oscilantes o cíclicas. El tiempo de simulación equivale a 45 segundos de carga en todos los casos. Las cargas aplicadas en las simulaciones 1D y 2D se realizaron considerando los parámetros que se muestran en la tabla 1. Las pruebas realizadas consideraron el CA como un material continuo y homogéneo con los condrocitos haciendo parte del continuo.
Tabla 1. Parámetros para las características del material homogéneo [34]
Table 1. Parameters for the homogeneous material characteristics [34]

3.1.2 Mallado
Para la simulación 1D, se realizó una malla que representa un fragmento de 0.3 mm de CA. A partir de esta malla se obtuvieron 641 nodos y 320 elementos de 3 nodos. En la simulación 2D se realizó una malla que representa un fragmento de 0.09 mm2 de cartílago articular (0.3mm x 0.3 mm). En este caso se obtuvieron 10.201 nodos que equivalen a 10.000 elementos de 4 nodos.
3.1.3 Condiciones de Contorno
La simulación se realizó de manera que no se permitió el desplazamiento en el eje y en la parte inferior. Se aplicó la carga en el borde superior, permitiendo la salida de fluido solamente en la parte inferior del fragmento de tejido, como se muestra en la figura 3a. Para 2D, se simuló una condición de confinamiento del tejido en la forma que indica la figura 3b, de manera que se presente flujo únicamente en la parte inferior. En la parte superior se colocó la carga y se restringió el movimiento lateral e inferior, condiciones similares a las reportadas en diversos trabajos experimentales, entre ellos el de Ateshian et al [10], Frijns [5] y Wu et al [34].
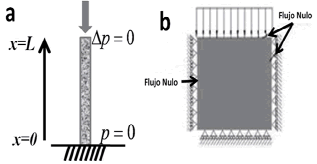
Figura 3. Esquema del CA en su condición de confinamiento en (a) 1D y (b) 2D
Figure 3. AC scheme for the confinement conditions in (a) 1D and (b) 2D
3.1.4 Condiciones de Carga
Los cálculos para simular la carga aplicada se realizaron a partir de los datos para el CA reportados por Wu et al [34]. Para las simulaciones 1D se aplicó una carga de -2.033 N/m en compresión, 2.033 N/m en tensión y cargas cíclicas con frecuencia equivalente a 0.1 Hz. En las simulaciones en 2D se aplicó una carga sobre la cara superior del fragmento de cartílago cuyo valor correspondió a -4.0397e-6 N/m en compresión, 4.0397e-6 N/m en tensión. Para cargas cíclicas se aplicó una frecuencia equivalente a 0.1 Hz.
4. RESULTADOS OBTENIDOS
4.1 Simulaciones 1D
4.1.1 Respuesta ante cargas de Compresión
Las respuestas obtenidas en las prueba ante cargas compresivas pueden observarse en las figura 4. En la figura 4a se observa el desplazamiento negativo del componente sólido que incrementa negativamente su valor a medida que aumenta el tiempo de carga, siendo inicialmente cero (0) para un t= 0.67s y llegando a cifras de -15x10-4 mmN-1s-1 en el tiempo máximo de carga, t=45s para x=0.3. A medida que fluye el líquido, el comportamiento se hace similar a un comportamiento elástico lineal, debido a que el único componente que soporta la carga es el sólido.
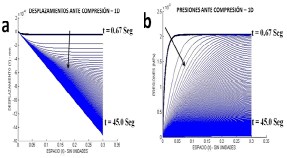
Figura 4. Respuesta del tejido a las fuerzas de Compresión a. Desplazamientos de la matriz sólida. b. Variación de la presión del fluido en el tejido ante el desplazamiento del mismo
Figure 4. Response of tissue to compression forces a. Displacement of solid matrix. b. Changes in the fluid pressure in the tissue in presence of the displacement of the same
En la figura 4b se observa la disminución de la presión debido a la salida del fluido ante la compresión del tejido. Para un tiempo inicial t=0.67s la presión que se ejerce sobre el fluido en el tejido es de 2 MPa, pero a medida que evoluciona la permanencia de la carga compresiva, la presión disminuye y toma valores cercanos a 0 MPa, con lo cual se equilibra la presión externa, también igual a cero.
4.1.2 Respuesta ante cargas de Tensión
La figura 5 resume los resultados obtenidos para fuerza de tensión. En la figura 5a se evidencia el desplazamiento positivo del componente sólido en respuesta a la carga tensil impuesta al tejido. Se aprecia cómo ante la tensión mantenida en el tiempo los desplazamientos se hacen positivos. Desde un valor inicial de 0 mmN-1s-1 en t= 0.67s, el desplazamiento aumenta hasta llegar al máximo de 16x10-4 mmN-1s-1 en un tiempo máximo de carga t=45s.
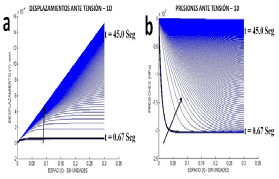
Figura 5. Respuesta del tejido ante fuerzas de tensión. a. Desplazamiento del componente sólido del tejido en sentido ascendente. b. Evolución de la presión del fluido generada por la redistribución del líquido dentro del tejido
Figure 5. Response of tissue in presence of tension forces. a. Displacement of solid component tissue upward. b. Change in the fluid pressure generated by the redistribution of fluid in the tissue
En la figura 5b se observa el incremento de la presión del fluido generada por el ingreso de éste hacía el interior del tejido debido a la diferencia de presiones entre el medio interno y el externo (succión del fluido). Esta diferencia de presiones es ocasionada por el desplazamiento del componente sólido en sentido positivo como respuesta a la carga tensil impuesta. Se evidencia como ésta progresión del incremento de la presión se presenta a través del tiempo realizando una redistribución del fluido en el tejido.
4.1.3 Respuesta ante cargas Oscilantes
Las respuestas obtenidas en la simulación de cargas oscilantes pueden observarse en la figura 6. En la figura 6a se observa la alternancia en los desplazamientos presentada en cada oscilación.
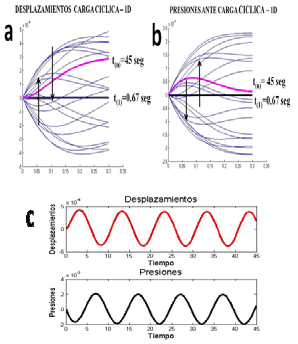
Figura 6. Respuesta ante cargas ciclicas. a. Desplazamientos alternos del componente sólido. b. Evolución de la presión del fluido de manera oscilante. c. Retardo entre la deformación del sólido y la variación de la presion del fluido
Figure 6. Response to cyclic load. a. Alternate displacement of the solid component. b. Changes in the fluid pressure in oscillate form. c. Delay between the solid deformation and fluid pressure variation
Inicialmente los desplazamientos del sólido son pequeños, cercanos a 0 mmN-1s-1 para t= 0.67s. Sin embargo, aumenta en el tiempo llegando a valores de 6x10-4 mmN-1s-1 ó -6x10-4 mmN-1s-1, en t=45s, según el tejido soporte cargas de tensión o compresión respectivamente. En la figura 6b se muestra el desarrollo del proceso de oscilación en las presiones del fluido en respuesta a los desplazamientos que sufre la matriz sólida al percibir la carga cíclica. Inicialmente la presión desciende para luego realizar un ajuste que la incrementa, estando en fase inversa con la evolución de la deformación de la fase sólida del tejido. Es decir, una vez el sólido se deforma en sentido positivo, la presión cambia haciéndose más negativa y viceversa.
La evidente alternancia en los procesos de deformación del sólido frente a la aplicación de cargas cíclicas demuestra que los desplazamientos son debidos a la carga ejercida sobre el tejido y a la movilización del fluido desde o hacia el interior su interior según se apliquen cargas compresivas o de tensión respectivamente. Estas cargas, a su vez, generan alternancia respecto a cada instante de tiempo entre el patrón de variación de la presión y el patrón de variación de los desplazamientos. Sin embargo, ésta acción no se encuentra en completa fase con los desplazamientos. Se puede apreciar la presencia de un retardo en los procesos alternantes anteriormente descritos, debido a que la ecuación que representa los desplazamientos es elíptica y corresponde a una ecuación de desplazamiento en el espacio en tanto que la ecuación que representa las presiones corresponde a una ecuación parabólica que representa un proceso difusivo mucho más lento que el proceso de desplazamiento (figura 6c).
4.2 Simulaciones 2D
4.2.1 Respuesta ante cargas de Compresión
La figura 7a corresponde al desplazamiento del sólido en el eje y para cada instante de tiempo. Los desplazamientos se hacen pequeños en los primeros momentos de la carga y se puede apreciar que a medida que incrementa el tiempo de carga el desplazamiento aumenta hacia valores más negativos, lo que demuestra una mayor deformación de la fase sólida del tejido. Estos desplazamientos se producen gracias a la salida del fluido en respuesta a la carga de compresión mantenida y se observa que el mayor desplazamiento se produce en las capas superiores del tejido, encargadas de recibir la carga de manera directa, mientras que la transferencia de desplazamiento es menor a mayor profundidad del tejido.
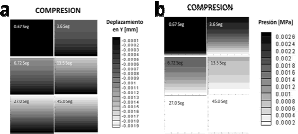
Figura 7. Respuesta 2D ante carga compresiva. a. desplazamientos ocurridos en y durante 45 segundos. b. Comportamiento de la presión del fluido pa causa de la salida del mismo por la carga
Figure 7. 2D response to compressive load. a. y displacements during 45 seconds. b. Behavior of the fluid pressure p due to its outflow in presence of the load
La figura 7b muestra el comportamiento de la presión del fluido en cada instante de tiempo. Se observa que la presión desciende rápidamente en todas las capas del tejido llegando a valores muy cercanos a 0 MPa en tiempos muy cortos. Esta variación de la presión del fluido corresponde a la disminución del mismo en función de la carga ejercida a través del tiempo y al comportamiento poroelástico del tejido que permite la salida del fluido.
4.2.2 Respuesta ante cargas de Tensión
Los resultados obtenidos a partir de la simulación en tensión se muestran en la figura 8. En la figura 8a se muestra el desplazamiento del sólido en el eje y para distintos instantes de tiempo. Se observan grandes desplazamientos en los primeros momentos de carga (t=0.67s) y la disminución del desplazamiento a medida que aumenta el tiempo de carga. Se observa además que ante una carga tensil mantenida en un tiempo dado, el mayor desplazamiento o elongación se produce en las capas superiores del tejido donde la tensión se percibe en primera instancia, razón por la cual la transferencia de deformación es menor a mayor profundidad del tejido. En este caso las presiones del fluido tienden a incrementarse porque el tejido busca un equilibrio entre el amiente interior y el ambiente exterior. El desplazamiento entonces se produce en respuesta a la tensión y origina una reorganización del fluido dentro del tejido, interfiriendo con la variación en las presiones del mismo.
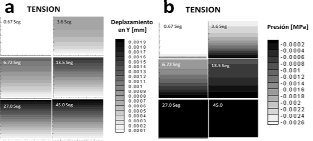
Figura 8. Respuesta en 2D ante carga tensil. a. desplazamientos ocurridos en y. b. comportamiento de la presión del fluido p a causa de la entrada del mismo por la tensión
Figure 8. 2D response to tensile load. a. y displacements. b. Behaviour of the fluid pressure p due to its inflow in presence of the load
La figura 8b muestra el comportamiento de la presión del fluido p para diferentes instantes de tiempo. Se observa que la presión del fluido se incrementa en pequeñas cantidades en respuesta a la carga tensil mantenida. Esta acción es debida a la compensación del tejido en respuesta a la deformación en elongación presentada por la fase sólida del tejido que obliga a una redistribución del fluido hacia el interior del tejido. Sin embargo, es evidente que al final del tiempo de carga tensil (aproximadamente en t= 27s), el tejido ya no puede sufrir mayor deformación en elongación y por lo tanto la presión del fluido también tiende a estabilizarse en el interior del mismo, lo que causa una presión mantenida estable cercana a cero que se equilibra con la presión externa.
4.2.3 Respuesta ante cargas Oscilantes
La figura 9a corresponde al desplazamiento del sólido en el eje y en diferentes instantes de tiempo. Se observa que los desplazamientos o deformaciones se producen de manera alternada ya que en los tiempos 1, 3 y 5 (t=0.67s, t=6.57s y t=27s respectivamente) el desplazamiento se hace positivo, comportamiento equivalente al observado durante la exposición a cargas de tensión. De manera inversa, en los tiempos 2, 4 y 6 (t=3.37s, t=16.5 s y t=45s respectivamente) el desplazamiento se hace negativo, lo que concuerda con el comportamiento que exhibe la matriz ante cargas de compresión.
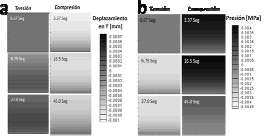
Figura 9. Respuesta en 2D ante carga oscilante. a. Desplazamientos alternados ocurridos en y b. Oscilación de la presión p dentro del tejido según la carga que se perciba
Figure 9. 2D response to oscillate load a. y displacements. b. Oscillation of the pressure p within the tissue according to the load
En la figura 9b se aprecia el comportamiento de la presión del fluido p. De manera semejante a lo ocurrido con las deformaciones de la fase sólida, se evidencia la oscilación de las presiones en respuesta a las cargas cíclicas impuestas al tejido. Nótese que en los tiempos 1, 3 y 5 (t=0.67s, t=6.57s y t=27s respectivamente) la presión tiende a disminuir a causa de la redistribución del fluido como respuesta a las cargas de tensión percibidas. Debido que las cargas no son mantenidas, el tejido no alcanza a compensar con entrada de fluido desde el exterior lo que explica que la presión no se incremente. De esta manera, en los tiempos 2, 4 y 6 (t=3.37s, t=16.5 s y t=45s respectivamente), la presión tienden a incrementar en respuesta a la compresión impuesta al tejido. Esto se debe a la rapidez con que se alternan las cargas compresivas y tensiles que evitan que el comportamiento del cartílago durante el período de carga cíclica corresponda exclusivamente al exhibido en los casos de tensión o compresión.
5. DISCUSION
Existen varias teorías que explican el comportamiento del CA ante condiciones de carga, resumidas en modelos de cómputo que incluyen el proceso inflamatorio y las propiedades de la estructura anisotrópica del colágeno. Las pruebas más utilizadas para determinar la calidad mecánica del CA son las pruebas de compresión confinada, compresión no confinada, identación e inflamación [16] llevadas a cabo utilizando herramientas de aproximación numérica.
Para efectos de cumplir los objetivos planteados en este trabajo se simuló una condición de confinamiento del tejido que permite el flujo en la parte inferior restringiendo el movimiento en sentido lateral e inferior, condiciones similares a las reportadas en experimentos prácticos como los trabajos presentados por Ateshian, et al [10], Frijns [5] y Wu et al. [34], entre otros. Los datos obtenidos a partir de las simulaciones realizadas confirman la teoría del comportamiento bifásico del cartílago articular, propuesta inicialmente por V.C. Mow et al. [7], y respaldada por diversos autores como M.A. Haider et al. [8], W. Wilson et al. [16], M.A. Haider et al. [17], X.N. Meng et al. [18], J.Z. Wu et al.[19], K. Terada et al. [20], P.S. Donzelli et al. [21] y P.S. Donzelli et al. [22], entre otros.
Los resultados encontrados nos permiten concluir que el cartílago articular exhibe una respuesta de desplazamiento de su componente sólido (matriz) y una variación en las presiones de su componente de fluido a causa de la salida o entrada del mismo, con disminución de la presión en respuesta a las cargas compresivas y aumento de la misma ante cargas tensiles. El desplazamiento es causado por la salida del fluido en respuesta a la carga de compresión mantenida. Sin embargo es importante resaltar que una vez que el tejido llega a su máximo desplazamiento, se comporta como un material sólido más que como un material poroelástico. A partir de este momento el fluido no puede fluir fuera del tejido porque la presión se ha equilibrado con la externa y el fluido empieza a soportar parte de la carga.
Si esta presión se mantiene por periodos prolongados puede causarse deshidratación del tejido y producirse cambios en su comportamiento habitual, haciéndolo más sensible a lesiones de manera temporal o permanente. Estos hallazgos permiten concluir que una carga mantenida de manera constante por largos periodos de tiempo o una carga excesiva que sobrepase las características del tejido, una vez ha alcanzado el máximo de desplazamiento posible, puede hacerlo más vulnerable a las lesiones por sobrecarga. Este hecho es motivo de discusión de un segundo artículo que incluye los procesos bioquímicos en respuesta a las cargas, como lo sugieren las investigaciones realizadas por Lucchinetti, et al. [37] y Chen, et al.[38], entre otros.
Los datos reportados son el inicio de trabajos más amplios en el estudio del tejido cartilaginoso que permitan incorporar el componente celular de manera diferencial y la bioquímica propia del cartílago en el modelo. Los resultados obtenidos motivan los esfuerzos que actualmente buscan simular la producción y destrucción de la matriz en presencia de cargas mecánicas, simular la remodelación del mismo después de una lesión, aplicar modelos matemáticos en el estudio del cartílago en crecimiento y estudiar su comportamiento in vitro e in vivo. Estas líneas de investigación pretenden brindar bases sólidas para el desarrollo de experimentos con CA in vivo e in vitro que permitan ampliar el rango de aplicaciones de las técnicas de simulación numérica y las técnicas usadas en ingeniería de tejidos.
6. AGRADECIMIENTOS
Los autores desean agradecer a la División de Investigación de Bogotá (DIB) de la Universidad Nacional de Colombia que en la convocatoria de Investigación 2008 apoyó el presente trabajo en el marco del proyecto Modelado Matemático y Simulación de Procesos en Ingeniería Mecánica y Biomédica.
REFERENCIAS
[1] LAWRENCE, R.C., HELMICK, CH.G., ARNETT, F.C.. Estimates of the prevalence of the arthritis and selected musculoskeletal disorders in the United States . Arthritis Rheum; 41: 2213-2218. 1998. [ Links ]
[2] DÍAZ CORTÉS, M. Guías de práctica clínica para el tratamiento de la osteoartritis de cadera, rodilla y mano. Revista Colombiana de Reumatología VOL. 9 No. 1, pp. 15-17, Marzo 2002. [ Links ]
[3] WU, J.P. and KIRK, T.B. A Study of the Shape Change of the Sheep Chondrocytes with Application of Compression to Cartilage. Seventh Australian and New Zealand Intelligent Information Systems Conference, Perth, Western Australia. 18-21 November 2001. [ Links ]
[4] ANDRIACCHI, T.P., MÛNDERMANN, A., SMITH, R.L., ALEXANDER, E.J., DYRBY, C.O., KOO, S. A framework for the in vivo pathomechanics of osteoarthritis at the knee. Annals of Biomedical Engineering 32, 447–457. 2004. [ Links ]
[5] FRIJNS, A.J.H. A Four-Component Mixture Theory Applied to Cartilaginous Tissues. Tesis Doctoral. Eindhoven University of Technology, 2000. [ Links ]
[6] DOBLARÉ CASTELLANO, M. Sobre el Modelado en Biomecánica y Mecano-biología. Discurso de ingreso a la Real Academia de Ciencias Exactas, Físicas, Químicas y Naturales de Zaragoza. 3 de noviembre del año 2005. [ Links ]
[7] MOW, V.C., KUEI, S.C., LAI, W.M., ARMSTRONG, C.G. Biphasic creep and stress relaxation of articular cartilage in compression: theory and experiments. Journal of Biomechanical Engineering 102: 73-84. 1980. [ Links ]
[8] HAIDER, M.A, SCHUGART, R.C. A numerical method for the continuous spectrum biphasic poroviscoelastic model of articular cartilage. Journal of Biomechanics 39, 177–183. 2006. [ Links ]
[9] WILSON, W., VAN DONKELAAR, C.C., VAN RIETBERGEN, B., ITOA, K., HUISKES, R. Stresses in the local collagen network of articular cartilage: a poroviscoelastic fibril-reinforced finite element study. Journal of Biomechanics 37, 357–366. 2006. [ Links ]
[10] ATESHIAN, G.A., WARDEN, W.H., KIM, J.J., GRELSAMER, R.P. and MOW, V.C. Finite deformation biphasic material properties of bovine articular cartilage from confined compression experiments. J. Bimechanics Vol 30. Nos. 11/ 12. pp 1157-1164. Published by Elsevier Science. 1997. [ Links ]
[11] CHAN, B., DONZELLI, P.S., and SPILKER, R.L. A Mixed-Penalty Biphasic Finite Element Formulation Incorporating Viscous Fluids and Material Interfaces. Annals of Biomedical Engineering, Vol. 28, pp. 589–597, 2000. [ Links ]
[12] MARTÍN HERNÁNDEZ, C. Estudio Mecánico, Histológico, e Histomorfométrico del Regenerado de Cartílago a Partir de Injertos de Periostio Invertido. Tesis Doctoral. Universidad Autónoma de Barcelona. 2002. [ Links ]
[13] MOW, V.C., KWAN, M.K., LAI, W.M., and HOLMES, M.H. A finite deformation theory for nonlinearly permeable soft hydrated biological tissues. Frontiers in Biomechanics. Ed by G.W. Schmid-Schönbein. S.L.-Y. Woo and B.W. Zwiefach. pp 153-179. Springer-Verlag. 1986. [ Links ]
[14] YANG, M. and TABER, L.A. The possible role of poroelasticity in the apparent viscoelastic behaviour of passive cardiac muscle. Journal of Biomechanics. 24(7): 587-597. 1991 [ Links ]
[15] POTTS, J.T., KRONENBERG, H.M., and ROSENBLATT, M. Parathyroid hormone: chemistry, biosynthesis, and mode of action. Advances In Protein Chemistry, 35:323–396, 1982. [ Links ]
[16] WILSON, W., VAN DONKELAAR, C.C., VAN RIETBERGEN, B., HUISKES, R. A fibril-reinforced poroviscoelastic swelling model for articular cartilage. Journal of Biomechanics 38, 1195–1204. 2005 [ Links ]
[17] HAIDER, M.A, GUILAK, F. Application of a three-dimensional poroelastic BEM to modelling the biphasic mechanics of cell–matrix interactions in articular cartilage. Computer methods in applied mechanics and engineering. 196, 2999–3010. 2007. [ Links ]
[18] MENG, X.N., LEROUX, M.A., LAURSEN, T.A., SETTON, L.A. A nonlinear finite element formulation for axisymmetric torsion of biphasic materials. International Journal of Solids and Structures 39, 879–895. 2002. [ Links ]
[19] WU, J.Z, HERZOG, W., EPSTEIN, M. An improved solution for the contact of two biphasic cartilage layers. J. Biomechanics Vol. 30, No. 4, pp 371.-375, 1997. [ Links ]
[20] TERADA, K., ITO, T., KIKUCHI, N. Characterization of the mechanical behaviors of solid-fluid mixture by the homoge nization method. Computer methods in applied mechanics and engineering. 153, 223-257. 1998. [ Links ]
[21] DONZELLI, P.S., SPILKER, R.L., ATESHIAN, G.A., MOW, V.C.. Contact analysis of biphasic transversely isotropic cartilage layers and correlations with tissue failure. Journal of Biomechanics 32, 1037-1047. 1998. [ Links ]
[22] DONZELLI, P.S., SPILKER, R.L. A contact finite element formulation for biological soft hydrated tissues. Computer methods in applied mechanics and engineering. 153, 63-79. 1998. [ Links ]
[23] ALMEIDA, E.S, SPILKER, R.L. Finite element formulations for hyperelastic biphasic soft tissues transversely isotropic. Computer methods in applied mechanics and engineering. 151, 513-538. 1998. [ Links ]
[24] WU, J.Z and HERZOG, W. Finite Element Simulation of Location- and Time-Dependent Mechanical Behavior of Chondrocytes in Unconfined Compression Tests. Annals of Biomedical Engineering, Vol. 28, pp. 318–330, 2000. [ Links ]
[25] LEVENSTON, M.E, FRANK, E.H., GRODZINSKY, A.J. Variationally derived 3-field finite element formulations for quasistatic poroelastic analysis of hydrated biological tissues. Computer methods in applied mechanics and engineering. 156, 231-246. 1998 [ Links ]
[26] HELMINEN, H. J. KIVIRANTA, I. TAMMI, M. ET AL. Joint Loading: Biology and Health of Articular Structures. Bristal, U.K. : Wrigth and Sons. 1987 [ Links ]
[27] MOW, V.C. and ATESHIAN, G.A. Lubrication and wear of diarthrodial joints. In V.C. Mow y W.C. Hayes (Eds.), Basic Biomechanics (2nd ed., pp 275-315) Philadelphia: Lippincott-Raven. 1997 [ Links ]
[28] SOPENA JUNCOSA, J.J., CARRILLO POVEDA, J.M., RUBIO ZARAGOZA, M., REDONDO GARCÍA, J.I., SERRA AGUADO, I., SOLER CANET, C.. Estructura y función del cartílago articular. Portada: Armas Frente a la Patología Articular. 2000 [ Links ]
[29] KOENIG, C. Curso de Histología. Oficina de Educación Médica. Escuela de Medicina. Pontificia Universidad Católica de Chile. http//escuela.med.puc.cl. [Consultado el 25 Noviembre 2007]. [ Links ]
[30] NORDIN, M. y FRANKEL V. Biomecánica Básica del sistema Musculoesqueletico. ED McGrawn-Hill Interamericana. Ed. 4ª. pp 61. 2004. [ Links ]
[31] WILSON, W. An explanation for the onset of mechanically induced cartilage damage. Tesis Doctoral. Technische Universiteit Eindhoven. Eindhoven, 2005. [ Links ]
[32] BUCKWALTER, J.A., MARTIN, J. Degenerative Joint Disease. Anatomy and physiology of sinovial joints. Clinical Symposia, Ciba, vol 47, nº 2, 1995. [ Links ]
[33] GARZÓN, D.A. Simulación de Procesos de Reacción-Difusión: Aplicación a la Morfogénesis del Tejido Óseo. Tesis doctoral. Centro Politécnico Superior de la Universidad de Zaragoza. Zaragoza, Mayo de 2007. [ Links ]
[34] WU, J.Z., HERZOG, W., EPSTEIN, M. Modelling of location- and time-dependent deformation of chondrocytes during cartilage loading. Journal of Biomechanics. 32: 563-572. 1999. [ Links ]
[35] RADI, M. Three-Dimensional Simulation of Thermal Oxidation. Dissertation. Institute for Microelectronics. Faculty of Electrical Engineering and information technology. 1998. http://www.iue.tuwien.ac.at/phd/radi [Consultado el 25 de Enero de 2007]. [ Links ]
[36] LAWRENCE. Curso de Materiales. Mechanical and aerospace engineering. University of Texas at Arlington. Consultado el 28 Enero de 2008. http://www-mae.uta.edu [ Links ]
[37] LUCCHINETTI, E., ADAMS, C.S, HORTON, W.E. Jr. and TORZILLI, P.A. Cartilage viability after repetitive loading: a preliminary report. Osteoarthritis and Cartilage 10: 71–81. 2002. [ Links ]
[38] CHEN, C.T., BHARGAVA, M., LIN, P.M., TORZILLI, P.A. Time, stress, and location dependent chondrocyte death and collagen damage in cyclically loaded articular cartilage. Journal of Orthopaedic Research 21: 888–898. 2003. [ Links ]














