Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.72 n.157 Medellín jan./abr. 2009
EFECTO DE LAS FORMAS DE ONDAS DE CORRIENTE PULSANTE EN LA ELECTRODEPOSITACIÓN DE NANOCRISTALES
EFFECT OF PULSE CURRENT WAVEFORMS IN NANOCRYSTALLYNE ELECTRODEPOSITION
JAROL MOLINA
Universidad Nacional de Colombia, Facultad de Minas, Medellín, jemolina@unal.edu.co
BIBIAN HOYOS
Universidad Nacional de Colombia, Escuela de Procesos y Energía, Medellín, bahoyos@unal.edu.co
Recibido para revisar febrero 18 de 2008, aceptado junio 18 de 2008, versión final julio 2 de 2008
RESUMEN: Se desarrolló un modelo matemático para establecer el efecto que tiene la forma de las ondas de corriente pulsante en el tamaño y dureza de nanocristales electrodepositados. El modelo relaciona de forma directa las variables típicas de las ondas (frecuencia, ciclo de trabajo y corriente pico) con la dureza de los depósitos generados mediante corriente continua y con cuatro tipos de ondas de corriente pulsante: rectangular, rampa ascendente, rampa descendente y triangular. Se evaluaron los resultados del modelo para ciclos de trabajo de 20 y 80%, con frecuencias de 50 y 150 Hz y corrientes pico de 4 y 8 kA/m2. El modelo predice que pequeños aumentos en el sobrepotencial de concentración incrementan significativamente la velocidad de nucleación, disminuyen el crecimiento de los nanocristales y generan un aumento en la dureza. El aumento del ciclo de trabajo y la frecuencia de las ondas produce un comportamiento cada vez más cercano al producido por la corriente continua, con una disminución en la dureza de los nanocristales. Cualquier modificación en las variables de las ondas, que tenga como consecuencia el incremento de la corriente pico, produce valores de dureza más altos.
PALABRAS CLAVE: Ondas de corriente, electrodepositación, nucleación, crecimiento, Modelo matemático.
ABSTRACT: A mathematical model has been developed for describing the effect of pulse current wave forms on size and hardness of electroplated nanocrystals. The model relates in a direct form the typical wave variables (frequency, duty cycle and peak current) with harness of generated deposits by means of direct current and by four pulse current wave forms: rectangular, ramp up, ramp down and triangular. The results of the model were evaluated for duty cycles of 20 and 80%, with frequencies of 50 and 150 Hz and peak currents of 4 and 8 kA/m2.The model predicts that small increases in the concentration overpotential drives to increase the nucleation rate significantly, diminishing the growth of the nanocrystals and generating a hardness increase. The increase of the duty cycle and the waves frequency produces a behavior increasingly close to that produced by direct current, with a diminution in the nanocrystals hardness. Any modification in the waveform variables that increases the peak current produces higher hardness values.
KEY WORDS: Pulse current, electroplating, nucleation, growth, Mathematical model.
1. INTRODUCCIÓN
Las investigaciones teóricas y experimentales para mejorar el proceso de electrodepositación han conducido a la propuesta de emplear técnicas como la electrodepositación por pulsos de corriente, sobre la cual existe un gran interés en la comunidad científica por comprender y explicar fenómenos como la formación, crecimiento y
coalescencia de los núcleos [1-3]. Estudios de los mecanismos de nucleación instantánea y progresiva cuando hay control mixto de transferencia de carga y difusión [4,5] son ejemplos típicos de investigaciones que se realizan alrededor de este proceso para mejorar su comprensión.
Se ha mostrado que el empleo de pulsos de corriente conduce al aumento en la pureza de nanocristales [6], con depósitos más homogéneos y de mayor densidad [7]. Esta técnica también se emplea, entre otras aplicaciones, en la fabricación de películas delgadas de alta dureza [8], en la electrodepositación de compuestos como Ni-Co [9] y Ni-SiC [10,11] y en la fabricación de electrodos para celdas de combustible obteniéndose excelentes desempeños [12].
En los últimos años ha aumentado la investigación encaminada a producir metales policristalinos y aleaciones de alta dureza mediante la reducción del tamaño de grano empleando corriente pulsante [9-12]. Como resultado de esto, se han llegado a producir industrialmente depósitos metálicos y aleaciones con tamaños de grano inferiores a 5 mm y con técnicas especiales de electrodepositación se han alcanzado tamaños de grano entre 10 y 20 nm [13]. Este tipo de materiales de tamaño fino se han denominado indistintamente como nanocristalinos, nanoestructurados o ultrafinos. Sin embargo, Hansen [13] propuso recientemente una clasificación para estos materiales teniendo en cuenta sus diferencias estructurales: cuando los granos están claramente delimitados y no se presenta prácticamente ninguna dislocación entre ellos, el material se clasifica como nanocristalino, mientras que materiales con ángulos de borde pequeños o con una mezcla de ángulos de borde altos y bajos, se denominan nanoestructurados. Los materiales nanoestructurados se producen típicamente por deformación plástica, mientras que los nanocristalinos generalmente se producen por condensación de gas o por electrodepositación.
En este artículo se presenta un modelo matemático que describe el efecto de la forma de la onda de corriente pulsante sobre el tamaño de grano y la dureza de depósitos nanocristalinos. Las formas de onda consideradas son: rampa ascendente, rampa descendente, onda triangular y onda rectangular.
En la literatura sobre el tema, existen algunos modelos para la descripción del sobrepotencial o de la velocidad de nucleación [14-17] pero dentro de nuestro conocimiento no hay uno que presente una relación funcional directa entre las variables que caracterizan a las ondas (frecuencia, ciclo de trabajo y corriente pico) con el tamaño de grano y la dureza de los depósitos. Con este modelo se presenta una nueva propuesta para el cálculo del tamaño final y promedio de los núcleos.
2. MODELO MATEMÁTICO
La concentración de especies electro-activas en la superficie del electrodo en un sistema donde la etapa controlante es la difusión, está descrita por la segunda ley de Fick (Ecuación 1):

con condiciones inicial y de frontera:
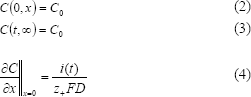
La función i(t) está definida por la forma de las ondas de corriente, las cuales se pueden representar matemáticamente con ayuda de la función impulso unitario o función de Heaviside, de tal manera que la ecuación diferencial parcial (ec. 1) se puede resolver empleando transformada de Laplace. En la tabla 1 se presenta la solución para la concentración en la superficie del electrodo y para el sobrepotencial (detalles de esta solución se pueden encontrar en Molina y Hoyos [18]).
Tabla 1. Perfiles de concentración y sobrepotencial para la onda rectangular, rampa ascendente, rampa descendente y triangular
Table 1. Concentration profiles and overpotential for the rectangular, ramp up, ramp down and triangular waveforms

Los parámetros que caracterizan las ondas de corriente son: el ciclo de trabajo (λ), la frecuencia (f) y la corriente promedio (iprom). Estos parámetros están definidos por las ecuaciones 5 a 8:
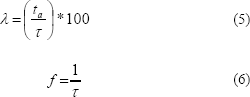
Para la onda de forma rectangular:

y para las ondas triangulares:
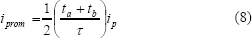
con tb = 0 para las rampas ascendente y descendente.
El tamaño de núcleo crítico, nc, definido como el aglomerado de la nueva fase que está en equilibrio inestable con la fase madre sobresaturada está definido en la ecuación 9.
Se habla de equilibrio inestable porque la unión de un átomo a un aglomerado de tamaño nc lo hace crecer irreversiblemente convirtiéndose en un aglomerado estable. Por el contrario, si se separa un átomo del aglomerado, este se disuelve de manera irreversible.
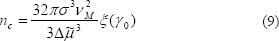
La función de ángulo mojado ξ(γo) que aparece en la ecuación 9, es la relación entre el volumen del segmento esférico del nanocristal formado y el volumen de una esfera completa con el mismo radio R:
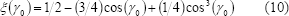
Para el caso de nucleación progresiva (nucleación y crecimiento simultáneos), la corriente total impuesta al sistema se emplea en los procesos simultáneos de nucleación y crecimiento:

La velocidad de nucleación está relacionada con la corriente de nucleación mediante la ec. 12:

Para el proceso de crecimiento de los núcleos, la realización de un balance de masa durante el crecimiento de un núcleo esférico individual en un proceso controlado por la transferencia de masa conduce a:
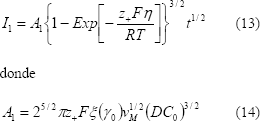
La corriente total de crecimiento de los nanocristales para un sistema con nucleación progresiva está dada por:
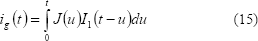
La ecuación 15 es una integral de convolución que contabiliza la corriente empleada en el crecimiento de los núcleos desde el momento en el cual nacen (u) hasta el tiempo t.
La relación entre la sobresaturación electroquímica, Δμ, y el radio, rc, del nanocristal formado que contiene 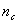 átomos está dada por:
átomos está dada por:

Con la corriente de crecimiento (ec.15) y la ley de Faraday se puede establecer el aumento del radio debido al crecimiento del núcleo a partir del momento en el cual nace:
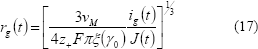
Finalmente la distribución del tamaño alcanzado por los nanocristales es:

Con la evaluación de un promedio másico y considerando una desviación estándar igual a cero para el radio de los núcleos, se puede obtener un diámetro promedio:
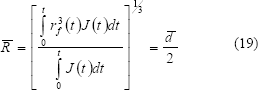
En este punto se debe resaltar que las ecuaciones 12, 17, 18 y 19 constituyen una nueva propuesta para el cálculo del tamaño final y promedio de los núcleos.
Una forma de relacionar el diámetro de los nanocristales depositados con sus propiedades mecánicas es emplear la relación Hall-Petch [15] que para el caso de la dureza se puede escribir como:
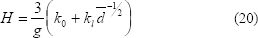
donde ko es un valor que depende del esfuerzo al cual comienza el movimiento de las dislocaciones, kl representa la penetrabilidad de la frontera de la dislocación móvil y g es la gravedad.
3. RESULTADOS Y DISCUSIÓN
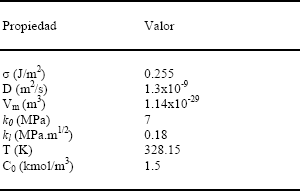
Con el objetivo de establecer el efecto que tiene la forma de la onda en el tamaño de los nanocristales y en su dureza, se comparan los resultados del modelo para las cuatro ondas de corriente pulsante y para corriente continua (modelada como una onda rectangular con un ciclo de trabajo de 100%). Con las ondas pulsantes se evalúa el efecto de la frecuencia, el ciclo de trabajo y la corriente pico. Se evaluaron los resultados del modelo para ciclos de trabajo de 20 y 80%, con frecuencias de 50 y 150 Hz y corrientes pico de 4 y 8 kA/m2. Los valores de las constantes físicas y los parámetros utilizados para la solución del modelo se muestran en la tabla 2.
Tabla 2. Propiedades físicas y parámetros empleados en el modelo
Table 2. Physical properties and parameters used in the model
En la figura 1 se puede apreciar el efecto del ciclo de trabajo sobre la dureza de los nanocristales: Cuando se aumenta el ciclo de trabajo a porcentajes cercanos al 100%, la forma de las ondas se aproxima cada vez más a la corriente continua, lo cual genera perfiles de concentración, sobrepotenciales y tamaños de grano similares a los generados por esta última forma de corriente. En consecuencia, para todos los casos, un mayor ciclo de trabajo produce depósitos menos duros (aproximándose al resultado obtenido con corriente continua). Se puede también observar que, para un mismo ciclo de trabajo, la rampa ascendente genera durezas levemente mayores a las otras ondas, pero esta diferencia no es significativa para estas condiciones.
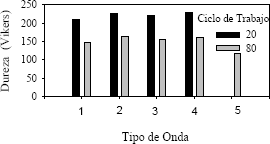
Figura 1. Variación en la dureza por modificación del ciclo de trabajo (iprom 2000 A/m2): 1 onda rectangular, 2 rampa ascendente, 3 rampa descendente, 4 onda triangular, 5 DC
Figure 1. Hardness variation by modification of the duty cycle (iprom 2000 A/m2): 1 rectangular, 2 ramp up, 3 ramp down, 4 triangular, 5 DC
Para el caso del efecto de la frecuencia (fig. 2) se puede ver que para altas frecuencias el sistema se acerca al caso de corriente continua y la dureza disminuye con respecto a la utilización de bajas frecuencias. También se debe observar que para que los cambios de dureza sean apreciables, hay que disminuir la frecuencia de forma significativa. Esto indica que el sistema es poco sensible a esta variable.
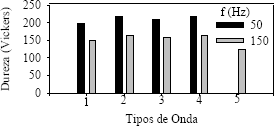
Figura 2. Variación en la dureza por modificación de la frecuencia (iprom 2000 A/m2): 1 onda rectangular, 2 rampa ascendente, 3 rampa descendente, 4 onda triangular, 5 DC
Figure 2. Hardness variation by modification of frequency (iprom 2000 A/m2): 1 rectangular, 2 ramp up, 3 ramp down, 4 triangular, 5 DC
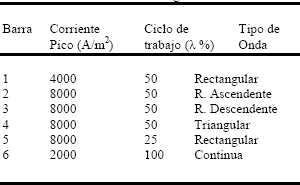
La influencia que tiene la corriente pico o máxima impuesta al sistema sobre la dureza se puede apreciar en la figura 3. En la tabla 3 se muestran las condiciones de corriente pico y ciclo de trabajo bajo las cuales fue realizada la simulación y que garantizan una corriente promedio de 2000 A/m2.
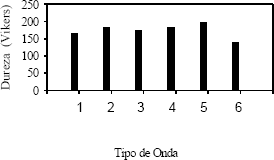
Figura 3. Dureza de los depósitos (iprom 2000 A/m2): 1 onda rectangular, 2 rampa ascendente, 3 rampa descendente 4 onda triangular todos con 50% de ciclo de trabajo, 5 onda rectangular (25% de ciclo de trabajo), 6 DC
Figure 3. Deposit harndness (iprom 2000 A/m2): 1 rectangular, 2 ramp up, 3 ramp down, 4 triangular, all the previous with 50% duty cycle, 5 rectangular (25% duty cycle), 6 DC
Tabla 3. Condiciones de ciclo de trabajo y corriente pico para los resultados de la figura 3
Table 3. Conditions of duty cycle and peak current for the results of figure 3
En la figura 3 se observa de forma clara que para la onda rectangular con un 25% de ciclo de trabajo (barra 5) y 8000 A/m2, el modelo produce un valor de dureza un poco mayor a la de las otras formas de corriente pulsante. El modelo también reporta que con corriente continua, la dureza es siempre menor.
El modelo desarrollado también permite establecer el efecto de los diferentes parámetros de la onda en el sobrepotencial (figura 4). El comportamiento del sobrepotencial es crítico ya que con altos sobrepotenciales se favorece la formación de nuevos nanocristales (nucleación) mientras que a bajos sobrepotenciales se favorece el crecimiento de ellos.
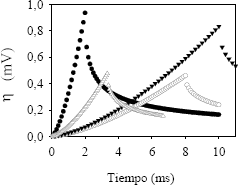
Figura 4. Sobrepotencial de concentración para la rampa Ascendente con iprom = 2000 A/m2: ● λ= 20% y 100 Hz; ○ λ = 80% y 100 Hz; ▼ λ= 50 % y 50 Hz; ∆ λ= 50% y 150 Hz
Figure 4. Concentration overpotential for the ramp up with iprom 2000 A/m2: ● λ= 20% and 100 Hz; ○ λ = 80% and 100 Hz; ▼ λ= 50% and 50 Hz; ∆ λ= 50% and 150 Hz
En la figura 4 se puede observar que, para una corriente promedio constante, el aumento de la frecuencia produce inicialmente un mayor aumento en el sobrepotencial de concentración, pero el valor máximo que se alcanza es menor que el alcanzado a bajas frecuencias. Por otra parte, una disminución del ciclo de trabajo produce inicialmente un drástico aumento en el sobrepotencial y un mayor valor de sobrepotencial máximo alcanzado, pero al final de la aplicación de la onda, el sobrepotencial ha caído a valores menores que los obtenidos con ciclos de trabajo mayores. Este comportamiento es similar para los diferentes tipos de onda de corriente considerados en este trabajo.
La figura 5 muestra que el modelo predice que los aumentos en el sobrepotencial de concentración incrementan significativamente la velocidad de nucleación, alcanzando las mayores velocidades de nucleación en los picos del sobrepotencial, con lo cual se establece que para bajos sobrepotenciales los nanocristales son de mayor tamaño y los depósitos son más blandos.
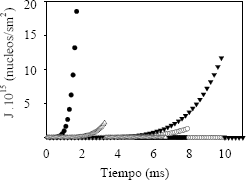
Figura 5. Velocidad de nucleación para la rampa Ascendente con iprom 2000 A/m2: ● λ= 20% y 100 Hz; ○ λ = 80% y 100 Hz; ▼ λ= 50 % y 50 Hz; ∆ λ= 50% y 150 Hz
Figure 5. Nucleation rate for the ramp up with iprom 2000 A/m2: ● λ= 20% and 100 Hz; ○ λ = 80% and 100 Hz; ▼ λ= 50% and 50 Hz; ∆ λ= 50% and 150 Hz
Como se observa en la figura 6, los parámetros de la onda que producen mayores sobrepotenciales y mayores velocidades de nucleación producen a su vez menores tamaños en la distribución final de los radios de los nanocristales formados. Como el tamaño de núcleo es más pequeño para el caso del mayor sobrepotencial, esto confirma el resultado de que la dureza del depósito sea mayor para el caso de sobrepotenciales más altos.
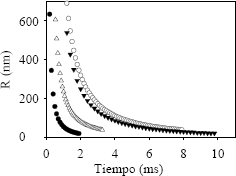
Figura 6. Radio de núcleo para la rampa Ascendente con iprom 2000 A/m2: ● λ= 20% y 100 Hz; ○ λ= 80% y 100 Hz; ▼ λ= 50 % y 50 Hz; ∆ λ= 50% y 150 Hz
Figure 6. Nucleus radii for the ramp up with iprom 2000 A/m2: ● λ= 20% and 100 Hz; ○ λ= 80% and 100 Hz; ▼ λ= 50% and 50 Hz; ∆ λ= 50% and 150 Hz
Otro resultado del modelo (fig. 7) muestra que la dureza tiene una relación directa con la corriente pico: cuando la corriente pico se incrementa ya sea por modificación del ciclo de trabajo o frecuencia, la dureza de los depósitos también se incrementa.
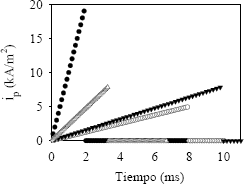
Figura 7. Perfil de corriente impuesta para rampa ascendente con iprom 2000 A/m2: ● λ= 20% y 100 Hz; ○ λ= 80% y 100 Hz; ▼ λ= 50 % y 50 Hz; ∆ λ=50% y 150 Hz
Figure 7. Imposed current profile for ramp up with iprom 2000 A/m2: ● λ= 20% and 100 Hz; ○ λ= 80% and 100 Hz; ▼ λ= 50% and 50 Hz; ∆ λ=50% and 150 Hz
Aunque en las figuras 4 a 7 se presenta el comportamiento del sobrepotencial, la velocidad de nucleación y la distribución de tamaños para el caso de la rampa ascendente, el comportamiento de estas variables es similar con los restantes tipos de ondas.
4. CONCLUSIONES
Se desarrolló un modelo matemático analítico para establecer el efecto de los diferentes parámetros de las ondas de corriente pulsante sobre la velocidad de nucleación, tamaño y dureza de nanocristales electrodepositados.
El modelo predice que pequeños aumentos en el sobrepotencial de concentración incrementan significativamente la velocidad de nucleación, disminuyen el crecimiento de los nanocristales y generan un aumento en la dureza.
El aumento del ciclo de trabajo y la frecuencia de las ondas produce un comportamiento cada vez más cercano al producido por la corriente continua, con una disminución en la dureza de los nanocristales.
Cualquier modificación en las variables de las ondas, que tenga como consecuencia el incremento de la corriente pico, produce valores de dureza más altos.
5. AGRADECIMIENTOS
Este trabajo se pudo llevar a cabo gracias a la financiación de COLCIENCIAS (código: 1118-08-17212) y de la dirección de investigación de Universidad Nacional de Colombia – Medellín (DIME)
NOMENCLATURA
Constantes y abreviaturas
Símbolos griegose Carga elemental del electrón.
i Corriente impuesta al sistema.
t Tiempo.
f Frecuencia.
g Constante de gravedad.
x Distancia al electrodo.
C Concentración de iones.
D Coeficiente de difusión.
F Constantes de Faraday.
H Dureza del depósito.
J Velocidad de nucleación.
R Constante de los gases ideales.
Radio promedio de los nucleos
T Temperatura.
C0 Concentración de iones en el estado inicial y en el seno de la solución.
i Corriente impuesta al sistema
ig Corriente de crecimiento.
iN Corriente de enucleación.
ip Corriente máxima o pico.
iprom Corriente promedio.
I1 Corriente de crecimiento de un núcleo individual.
kl Constante experimental de la ecuación de Hall-Petch.
k0 Constante experimental de la ecuación de Hall-Petch.
nc Tamaño de núcleo critico.
rc Radio critico de un aglomerado.
rf Radio final de un aglomerado.
rg Radio de crecimiento.
Sk Función de Heaviside.
ta Tiempo de corriente activa.
tb Tiempo de corriente activa (Onda triangular).
vM Volumen molecular.
z+ Carga del ion.
Potencial electroquímico.
η Sobrepotencial (En este caso particular sobrepotencial de concentración).
Sobrepotencial de concentración para la onda rectangular.
Sobrepotencial de concentración para la onda rampa ascendente.
Sobrepotencial de concentración para la onda rampa descendente.
Sobrepotencial de concentración para la onda triangular.
Γ Función Gamma.
γ0 Angulo de contacto o ángulo mojado del aglomerado con el sustrato.
Función de ángulo mojado.
σ Energía libre especifica interracial.
λ Ciclo de trabajo.
τ Tiempo total de un ciclo.
REFERENCIAS
[1] SCHARIFKER, B. AND HILLS, G. Theoretical and experimental studies of multiple nucleation, Electrochimica Acta, 28, 7, 879-889, 1983. [ Links ]
[2] MOSTANY, J., SERRUYA, A. AND SCHARIFKER, B. Spatial distribution of electrodeposited lead nuclei on to vitreous carbon beyond their nearest neighbours, J. Electroanalytical Chemistry, 383, 37–41, 1995. [ Links ]
[3] SERRUYA, A., MOSTANY, J. AND SCHARIFKER, B. The kinetics of mercury nucleation from Hg22+ and Hg2+ solutions on vitreous carbon electrodes, J. Electroanalytical Chem., 464, 39–47, 1999. [ Links ]
[4] ALEXANDER, M. AND ZAPRYANOVA, T. Nucleation and growth of copper under combined charge transfer and diffusion limitations: Part I, Electrochimica Acta, 51, 2926–2933, 2006. [ Links ]
[5] MILCHEV, A. AND ZAPRYANOVA, T. Nucleation and growth of copper under combined charge transfer and difusión limitationsPart II, Electrochimica Acta, 51, 4916– 4921, 2006. [ Links ]
[6] YOUSSEF , KH. M. S., KOCH, C. C. AND FEDKIW, P. S. Influence of Additives and Pulse Electrodeposition Parameters on Production of Nanocrystalline Zinc from Zinc Chloride Electrolytes, J. Electrochemical Soc., 151, 2, C103-C111, 2004. [ Links ]
[7] KIM, B., RITZDORF, T. Electrical Waveform Mediated Through-Mask Deposition of Solder Bumps for Wafer Level Packaging, J. Electrochemical Soc., 151, 5, C342-C347, 2004. [ Links ]
[8] IBAÑEZ, A., FATÁS, E. Mechanical and structural properties of electrodeposited copper and their relation with the electrodeposition parameters, Surface & Coatings Techno., 191, 7–16, 2005. [ Links ]
[9] HANSAL,W. E.G., TURY, B., HALMDIENST, M., VARSÁNYI, M. L. AND KAUTEK, W. Pulse reverse plating of Ni–Co alloys: Deposition kinetics of Watts, sulfamate and chloride electrolytes, Electrochimica Acta., 52, 1145–1151, 2006. [ Links ]
[10] HU, F. AND CHAN, K. C. Electrocodeposition behavior of Ni–SiC composite under different shaped waveforms, Applied Surf. Sci., 233, 163–171, 2004. [ Links ]
[11] HU, F. AND CHAN, K. C. Deposition behaviour and morphology of Ni–SiC electro-composites under triangular waveform, Applied Surf. Sci., 243, 251–258, 2005. [ Links ]
[12] KIM, H. AND NALINI P. Subramanian, Branko N. Popov, Preparation of PEM fuel cell electrodes using pulse electrodeposition, J. Power Sour., 138, 14–24, 2004. [ Links ]
[13] HANSEN, N. HALL–PETCH relation and boundary strengthening, Scripta Materialia, 51, 801–806, 2004. [ Links ]
[14] WONG, K. P., CHAN, K. C., AND YUE, T. M. A study of hardness and grain size in pulse current electroforming of nickel using different shaped waveforms, J. Appl. Electrochem., 31, 25-34 2001. [ Links ]
[15] WONG, K. P., CHAN K. C. AND YUE, T. M. Modelling the effect of complex waveform on surface finishing in pulse current electroforming of nickel, Surface and Coating Technology, 135, 91-97, 2001. [ Links ]
[16] WONG K. P., CHAN K. C. AND YUE, T. M. Modelling of electrocrytallization for pulse current electroforming of nickel, Appl. Surf. Sci., 178, 178-189, 2001. [ Links ]
[17] GEORGIADOU M. AND VEYRET, D. Modeling of Transient Electrochemical Systems Involving Moving Boundaries, J. Electrochemical Soc., 149, 6, C324-C330, 2002. [ Links ]
[18] MOLINA J. E. Y HOYOS B. A. Modelo Matemático de la Nucleación Electroquímica con Ondas de Corriente Pulsante, Información Tecnológica., 18, 5, 31–40 2007. [ Links ]














