ANÁLISIS DE LA INESTABILIDAD DE TURING EN MODELOS BIOLÓGICOS

ANALYSIS OF TURING INSTABILITY IN BIOLOGICAL MODELS

 

JUAN VANEGAS
Maestría en Ingeniería Biomédica, Universidad Nacional de Colombia, jcvanegasa@ieee.org

NANCY LANDINEZ
Maestría en Ingeniería Biomédica, Universidad Nacional de Colombia, nslandinezp@unal.edu.co

DIEGO GARZÓN
Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia, dagarzona@unal.edu.co

 

Recibido para revisar marzo 12 de 2008, aceptado noviembre 12 de 2008, versión final noviembre 24 de 2008

 

---

RESUMEN: El análisis matemático de modelos biológicos descritos por ecuaciones de reacción difusión da lugar al concepto de inestabilidad de Turing. En este artículo se analiza este concepto y el espacio matemático en donde tiene lugar, conocido como espacio de Turing. El objetivo es establecer la relación entre el conjunto de parámetros que definen la presencia de patrones espacio-temporales en un sistema de reacción difusión. Estos parámetros son validados mediante la implementación numérica por el método de los elementos finitos en 1D y 2D de dos modelos conocidos: el modelo de Schnakenberg y el modelo de glucólisis. Los resultados demuestran que los parámetros obtenidos mediante el análisis matemático cumplen las restricciones de Turing y permiten la formación de patrones espacio-temporales. Se concluye que el análisis matemático de estabilidad es una herramienta útil para la obtención de parámetros desconocidos en modelos que usualmente requieren de ajustes mediante experimentación numérica.

PALABRAS CLAVE: Inestabilidad de Turing, reacción-difusión, formación de patrones, biología matemática.

ABSTRACT: The mathematical analysis of biological models described by reaction-diffusion equations gives place to the idea of Turing Instabilities. In this work we study this idea and the mathematical space upon which is supported, known as Turing Space. The aim is to establish the relationship between the set of parameters that define the presence of spatial-temporal patterns in the solution of a reaction-diffusion system. These parameters are validated in 1D and 2D by the implementation through the finite element method of two well-known biological models: the Schnakenberg model and the glycolysis model. The results show that the parameters obtained by the mathematical analysis lead to the formation of spatial-temporal patterns. We concluded that the mathematical analysis of stability is a useful tool for the selection of unknown parameters in a model that otherwise might require of adjustment through numerical experimentation.

KEYWORDS: Turing instability, reaction-diffusion, pattern formation, mathematical biology.

---

 

1. INTRODUCCIÓN

La formación de patrones espacio temporales ha sido analizada mediante diversos tipos de modelos matemáticos [1, 2, 3, 4, 5]. Desde el punto de vista biológico, los patrones formados por estos modelos pueden ser clasificados en dos categorías: patrones químicos y patrones de movimiento celular [2]. En la categoría de patrones químicos se tienen dos tipos de modelos: los modelos de gradiente y los modelos de reacción-difusión [1, 2]. Los modelos de gradiente son aquellos que generan patrones espacio temporales a partir de la descripción de la interacción entre sustancias químicas con diferencias de concentración. Estos gradientes de concentración dan lugar a que el sistema tienda a un estado uniforme en el espacio a lo largo de su evolución temporal. Por su parte, los modelos de reacción-difusión describen las interacciones químicas que generan patrones complejos en el espacio y/o el tiempo, debido a la presencia de términos de transporte, síntesis y degradación que dependen de todas las sustancias químicas presentes en el dominio de análisis [2, 6]. Por su parte, los modelos de movimiento celular analizan la formación de patrones espaciales debido a cambios de densidad celular, por agregación o repulsión entre las células, o por respuesta a sustancias químicas concretas [7].

En 1952 A. Turing [8] fue el primero en observar y atribuir a las interacciones químicas entre sustancias la auto-formación de patrones en la naturaleza y estudió las soluciones de los modelos biológicos descritos por ecuaciones de reacción-difusión. En ellas encontró que pueden existir tres tipos de inestabilidades: a) oscilatorias en el tiempo y uniformes en el espacio, relacionadas con las inestabilidades de Hopf independientes del espacio, b) estacionarias en el tiempo y periódicas en el espacio, y c) oscilatorias en el espacio y en el tiempo [3]. Turing demostró además que un sistema químico de reacción-difusión puede evolucionar hacia patrones espaciales heterogéneos desde un estado estacionario uniforme en respuesta a pequeñas perturbaciones [1, 2, 4, 9]. Conforme a esto, estableció que la difusión puede llevar un sistema químico a la inestabilidad, induciendo así la formación de un patrón espacial donde antes no existía. Este tipo de inestabilidad, estacionaria en el tiempo, es más conocida como inestabilidad de Turing [4, 5, 9, 10].

En este artículo se describe el análisis matemático de la inestabilidad de Turing para dos modelos biológicos conocidos [2, 6, 9, 10, 11]: el modelo de Schnakenberg, utilizado en morfogénesis, y el modelo de glucólisis, que describe el proceso de síntesis de la molécula de glucosa para proporcionar la energía necesaria para el metabolismo celular. En la sección II se enuncian los modelos biológicos utilizados y en la sección III se describe el análisis de estabilidad utilizado. En la sección IV se aplican los criterios de estabilidad obtenidos a los modelos señalados y en la sección V se discuten los resultados.

 

2. MODELOS BIOLÓGICOS

Existen diferentes modelos biológicos que permiten obtener una descripción matemática de fenómenos complejos presentes en la naturaleza [1, 5, 6, 7, 9]. Dos modelos bien referenciados, formulados por ecuaciones de reacción difusión, son el modelo de Schnakenberg, o modelo de morfogénesis [2, 4, 9, 10], y el modelo de glucólisis [2, 9, 11], utilizado para explicar la síntesis de glucosa en energía celular. Estos dos modelos generan patrones espaciales y cumplen con los criterios de estabilidad de Turing analizados en este artículo.

2.1 Modelo De Schnakenberg
El modelo de Schnakenberg es conocido como uno de los modelos de reacción difusión más sencillo y más utilizado en morfogénesis. En su forma adimensional, el modelo está descrito por [2, 9, 11]:

(1a)

(1b)

Este modelo explica el comportamiento de un químico activador en presencia de un químico inhibidor. Si u es el químico activador, la reacción cinética es tal que en la ecuación (1a) el término u²v representa la producción de u en presencia de v, en tanto que en (1b) el mismo término representa el consumo de v en presencia de u [2, 5]. Las constantes a, b, d y g son todas parámetros positivos, siendo a y b valores de producción, g una constante adimensional y d el coeficiente de difusión [2, 11].

2.2 Modelo De Glucólisis
La glucólisis o glicólisis es el proceso de síntesis de la molécula de glucosa para proporcionar energía al metabolismo celular. A través de una secuencia de reacciones, la glucosa es transformada en piruvato y en ATP, la unidad de intercambio metabólico en el organismo vivo [9, 11]. El modelo está representado por:

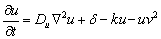(2a)

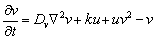(2b)

La interpretación biológica es similar al modelo de Schnakenberg, con u la concentración de glucosa, v la producción de piruvato, D_u y D_v los coeficientes de difusión, el término u²v representando consumo no lineal de u y el término uv² representando la activación no lineal de v. d es un parámetro positivo que representa una cantidad inicial de glucosa. El parámetro k, también positivo, representa en u el consumo natural de glucosa, mientras que en v representa la producción, en la misma proporción, de piruvato.

 

3. CONDICIONES GENERALES PARA LA INESTABILIDAD DE TURING

Supóngase que en (1) y (2) los términos difusivos (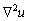,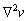) son cero y que existe un estado estacionario estable. Si al incluir nuevamente los términos difusivos el sistema no alcanza un estado estacionario estable, se dice entonces que (1) y (2) presentan inestabilidades por difusión o inestabilidades de Turing [9].

El análisis matemático de la inestabilidad de Turing predice el tipo y forma de los patrones emergentes de la solución temporal de las ecuaciones de reacción-difusión [2, 5, 9]. El primer paso del análisis es desacoplar el término de difusivo para garantizar la estabilidad temporal. Luego se reincorpora este término difusivo y se determina el espacio de parámetros que producen la inestabilidad espacial [1, 2, 9]. Esta metodología aplica para un sistema de reacción-difusión clásico de dos químicos u y v definido por:

(3.1.)

(3.2.)

donde f y g son las funciones de reacción. Se asumen condiciones de flujo en el contorno iguales a cero para garantizar que el patrón espacial formado se deba únicamente a la organización al interior del contorno, y no a flujos externos [9]. En ausencia de difusión, el sistema en (3) queda reducido a:

(4.1.)

(4.2.)

El estado estable de (3) es (u,v)=(u₀,v₀) tal que:

(5)

La inestabilidad de Turing tiene lugar cuando el estado estacionario (u₀,v₀), es estable en ausencia de difusión y se torna inestable en presencia del término difusivo. Si se define x y h como unas pequeñas perturbaciones del estado estable tal que (u,v)=(u₀+x, v₀+h), y se desarrolla (4) en series de Taylor alrededor del punto (u,v), (despreciando los términos de orden mayor e igual a 2 de x y de h) se tiene [2, 12]:

(6)

que puede rescribirse en su equivalente matricial (7) donde X=[x h]^T y J es la matriz jacobiana evaluada en el punto (u₀,v₀).

(7)

De la teoría de las ecuaciones diferenciales ordinarias se conoce que la solución de (7) tiene la forma [13]:

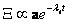(8)

donde l_t es un autovalor de J y a es su correspondiente autovector. Reemplazando (8) en (7) se obtiene que el estado homogéneo (u₀,v₀) es linealmente estable si los autovalores l_t de la matriz jacobiana J tienen parte real negativa. Para ello se debe cumplir que:

(9)

Tomando el determinante de (9) de obtiene la siguiente relación:

(10)

Resolviendo para l_t se tiene:

(11)

De 10 se obtiene que las condiciones para que los autovalores l_t tengan parte real negativa, conforme a los criterios de Routh-Hurwitz, son [14]:

(12a)

(12b)

Las condiciones en (12) garantizan la estabilidad lineal en el tiempo del estado estable homogéneo en ausencia de variaciones espaciales, es decir, sin difusión. En presencia de difusión, la linealización alrededor del estado estable es [2]:

(13)

donde X y J son como en (7) y D es una matriz diagonal de coeficientes de difusión. Si se considera que la solución del sistema es de la forma X=X(x)T(t) y se resuelve (13) por separación de variables, teniendo en cuenta que la solución debe cumplir las condiciones de contorno de flujo nulo 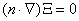, se obtiene un par de ecuaciones de la forma:

(14a)

(14b)

con k el autovalor de la ecuación o número de onda para el caso de las ecuaciones de reacción difusión. La solución de (14a) tiene la forma [13]:

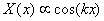(15)

con k=np, y n entero. La solución general de (13) es la combinación lineal de todos los términos que satisfacen (15), y el término temporal de (14b):

(16)

donde F_k son coeficientes de la serie de Fourier. Reemplazando (16) en (13) y linealizando se obtiene:

(17)

Como se busca una solución no trivial para (13) se debe satisfacer:

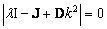(18)

Se requiere hallar l=l(k²), así que resolviendo (18) se obtiene la ecuación de dispersión asociada:

(19)

con:

(20)

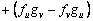(21)

La inestabilidad de Turing, inducida por difusión, ocurre cuando una de las raíces de (19) cumple que Re(l)>0 para algún k²>0. Esto es cierto si se cumple c(k²)>0 y b(k²)<0, o viceversa [2, 12]. Considerando (12a), D₁>0 y D₂>0, se obtiene b(k²) >0. Luego, para que exista inestabilidad de Turing se debe cumplir c(k²) <0 para todo k². De (12b) y de las condiciones D₁>0 y D₂>0, se obtiene que la condición para c(k²) se cumple si:

(22)

Sin embargo, (22) es condición necesaria pero no suficiente para que c(k²) <0, por lo que se debe cumplir además que el mínimo c_min sea negativo. Derivando (21) respecto a k² e igualando a cero se obtiene:

(23)

Reemplazando (23) en (21) y resolviendo, se obtiene la última condición para el análisis de la inestabilidad de Turing en sistemas de reacción difusión:

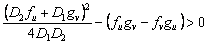
(24)

En resumen, las condiciones que restringen el espacio de parámetros, y que dan lugar al espacio de Turing, se define por el conjunto de las siguientes desigualdades [2, 12]:

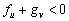(25a)

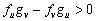(25b)

(25c)

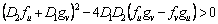(25d)

Sin embargo, si en (19) se cumple que c(k²)=0, se obtiene un parámetro de bifurcación donde el sistema puede ser estable o inestable [12, 15]. Esto da lugar a una condición adicional para la inestabilidad por difusión relacionada con la existencia de un número de onda k² que permita la formación del patrón espacial inestable. Esta nueva condición está dada por las raíces de (21), es decir:

(26a)

(26b)

donde:

(27a)

(27b)

Se puede verificar que en el caso c(k²)=0 existe un valor crítico d_c para la relación de difusión d=D₂/D₁ que condiciona la posible aparición de patrones de Turing. Resolviendo (21) para c(k²)=0 se obtiene el valor crítico d_c a partir de la solución de:

(28)

Este valor crítico d_c es el valor de difusión límite a partir del cual aparece el espacio de Turing y dentro del cual se cumplen las condiciones dadas en (25). De (28) se obtienen dos raíces solución, una de las cuales es descartada por no cumplir con (25). La otra raíz es el valor crítico de difusión d_c.

El análisis matemático puede extenderse a problemas bidimensionales resolviendo (14a) de forma separada para cada dimensión. La expresión bidimensional equivalente a (16) queda escrita como [2]:

(29)

con k²= k₁²+k₂² =(mp)²+(np)², m y n enteros. Como el número de onda debe estar asociado al menos a una posible solución de (29), k² debe ser tal que satisfaga la condición de estabilidad por difusión descrita en (26).

 

4. RESULTADOS DEL ANÁLISIS

Para verificar el análisis matemático de la sección anterior, se procede a realizar su aplicación en los modelos biológicos mencionados en la sección II. Se presentan resultados para los modelos unidimensionales y se aprovecha la extensión formulada a partir de (29) para ilustrar el caso bidimensional.

4.1 Modelo De Schnakenberg
A partir de las ecuaciones (1) y eliminando el término difusivo para obtener el estado estacionario uniforme de la expresión (4) se obtiene:

(30a)

30b)

De (30) se puede calcular explícitamente el estado estacionario, dado por (u₀,v₀)=(a+b,b/(a+b)²). Asumiendo a=0.1 y b=0.9, se obtiene (u₀,v₀)=(1.0,0.9). Por su parte, los valores de la matriz jacobiana J necesarios para el resto del análisis son:

(31a)

(31b)

(31c)

(31d)

Para hallar las condiciones críticas a partir de las cuales se encuentran patrones de Turing se utiliza la expresión (28) de donde se obtiene:

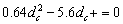(32)

A partir de (32) se obtienen las raíces d_c=0.1824 y d_c= 8.5676. De (19) se sabe que para que exista inestabilidad de Turing c(k²)<0 para todo k². Esto se corrobora graficando el término c(k²) para diferentes valores de d (figura 1). La condición de inestabilidad Re(l)>0 para algún k²>0 se verifica mediante la gráfica de la parte real de (19) (figura 2) [12]. Se observa que para d<d_c no se cumplen las condiciones de inestabilidad. Para el caso d=d_c, se obtiene el valor de k crítico de la expresión (23), mientras que para d>d_c se obtiene un espacio de inestabilidad limitado por los valores k_min y k_max dados por la expresión (26). Conforme a lo anterior, y en virtud de los criterios en (19), queda justificada la escogencia de un valor d>d_c que para el caso particular es d=10.

Figura 1. Término c(k²) de la expresión (21) para el modelo de Schnakenberg.
Figure 1. The term c(k²) in the expression (21) for the Schnakenberg model.

Figura 2. Parte real de los autovalores en (19) para el modelo de Schnakenberg.
Figure 2. Real part of the eigenvalues in (19) for the Schnakenberg model.

Ahora supóngase un dominio 0 ≤ x ≤ 1. Como los autovalores normalizados del sistema en una dimensión están dados por la expresión [2]:

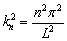(33)

se obtiene que k=np, donde n es un valor entero que representa el número de períodos existente en la solución (teniendo en cuenta además que la función coseno es par). Por lo tanto, para las anteriores condiciones se encuentra un intervalo de posibles números de onda dado por:

(34)

Utilizando la expresión (26) conforme a la adimensionalidad de (1) [15] y reemplazando los parámetros seleccionados se obtiene:

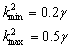(35)

Si se supone g=0, no habrá formación de patrones y, debido a las condiciones iniciales, el sistema llegará a su estado estacionario uniforme en el tiempo [12]. Luego, para valores de g<0, existe inestabilidad de Turing y conforme a su valor el sistema exhibirá diferentes comportamientos. Si se considera el caso g=30, el intervalo de formación de patrones estará dado por:

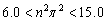(36)

Es decir:

(37)

Luego, el único valor entero para n es n=1. Para el caso g=250 se tiene:

(38)

de donde el único valor entero para n es n=3, es decir, un número de onda igual a 3. Las figuras 3 y 4 muestran el resultado para el caso g=30 resolviendo (1) mediante el método de los elementos finitos [16, 17, 18]. Para todos los casos se ha utilizado un PC con procesador AMD Turion 64 X2 doble núcleo de 1.6GHz y 2GB de memoria RAM. Las flechas señalan la dirección de la evolución desde el estado estacionario uniforme t=0 hacia el estado inestable espacial t=5. Los parámetros de la simulación son a=0.1, b=0.9, d=10 y g=30. Se requirieron 50 iteraciones y un paso de tiempo Dt=0.1.

Figura 3. Concentración de u para el modo n=1. Modelo de Schnakenberg en 1D
Figure 3. Concentration of u for the mode n=1. Schnakenberg model in 1D

Figura 4. Concentración de v para el modo n=1. Modelo de Schnakenberg en 1D
Figure 4. Concentration of v for the mode n=1. Schnakenberg model in 1D

Las figura 5 y 6 muestran el resultado para el caso g=250. Los parámetros de simulación se mantienen conforme al caso anterior. Se utilizaron 100 iteraciones y un paso de tiempo Dt=0.05.

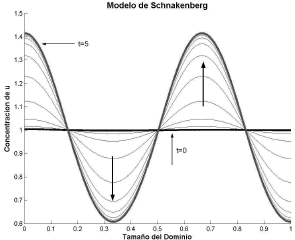
Figura 5. Concentración de u para el modo n=3. Modelo de Schnakenberg en 1D
Figure 5. Concentration of u for the mode n=3. Schnakenberg model in 1D

Figura 6. Concentración de v para el modo n=3. Modelo de Schnakenberg en 1D
Figure 6. Concentration of v for the mode n=3. Schnakenberg model in 1D

Es posible utilizar el mismo procedimiento para encontrar los parámetros de un modelo bidimensional. Sin embargo, debido a la presencia del término coseno adicional en (29), los autovalores del problema bidimensional en adoptan la forma [2]:

(39)

Si se escogen los parámetros de estado establece usados en el caso correspondiente a las figuras 3 y 4 pero se escoge d=9.1676 y g=176.72, al resolver (26) y (39) para un dominio [0,1] x [0,1] se obtiene:

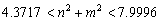(40)

Si se selecciona m=2, entonces el único valor entero que pertenece al intervalo y que puede adoptar n es n=1. Este modo de onda (2,1) se ilustra en la figura 7. En ella, a) y b) son las concentraciones para u y v respectivamente. Las dos imágenes corresponden al tiempo t=50. Los parámetros de la simulación son a=0.1, b=0.9, d=9.1676 y g=176.72. Se requirieron 1.000 iteraciones y un paso de tiempo Dt=0.05. La solución se hace sobre una malla de elementos cuadriláteros bilineales de 25 x 25 definida en un dominio de [0,1] x [0,1].

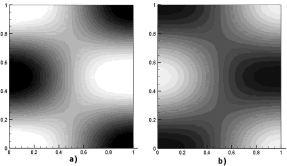
Figura 7. Concentraciones de u y v para el modo (2,1). Modelo de Schnakenberg en 2D
Figure 7. Concentrations of u and v for the mode (2,1). Schnakenberg model in 2D

Finalmente, si se escoge d= 8.6676 y g=230.82 y se repite el procedimiento anterior se obtiene la siguiente expresión:

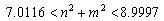(41)

de donde se obtiene que los únicos valores enteros que pueden tomar n y m son n=m=2, es decir, un modo de onda (2,2). Este modo es ilustrado en la figura 8. En ella, a) y b) son las concentraciones para u y v respectivamente. Las dos imágenes corresponden al tiempo t=20. Los parámetros son a=0.1, b=0.9, d=8.667 y g=230.82. Se requirieron 1.000 iteraciones y un paso de tiempo Dt=0.02. Se utilizó una malla de elementos cuadriláteros bilineales de 25 x 25 definida en un dominio de [0,1] x [0,1].

Figura 8. Concentraciones de u y v para el modo (2,2). Modelo de Schnakenberg en 2D
Figure 8. Concentrations of u and v for the mode (2,2). Schnakenberg model in 2D

4.2 Modelo De Glucólisis
De manera alterna al modelo de Schnakenberg, se ha realizado el análisis de estabilidad del modelo de glucólisis descrito en (2). Eliminando el término difusivo, se obtiene:

(42a)

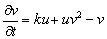(42b)

De (42), es posible calcular el estado estacionario, dado por (u₀,v₀)=(δ/(δ²+k),δ). Asumiendo d=1.2 y k=0.06, se obtiene (u₀,v₀)=(0.8,1.2). Similar a (31), los valores de la matriz jacobiana J asociada son:

(43a)

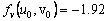(43b)

(43c)

(43d)

Reemplazando (43) en (28) se obtienen como valores críticos de difusión las raíces d_c=0.0991 y d_c=3.7942. Graficando el término c(k²) de (21) para diferentes valores de d (figura 9), y la parte real de (19) (figura 10), se verifican los valores de d para los cuales existe inestabilidad de Turing. A diferencia del modelo de Schnakenberg, para d>d_c no se cumplen las condiciones de estabilidad asociadas a (19). Si bien d=d_c continua siendo el valor de difusión crítico, es para d<d_c que existe inestabilidad de Turing asociada. Este hecho se corrobora observando que en la figura 9 la condición c(k²) <0 se cumple para d<d_c, de la misma forma que en la figura 10 es para d<d_c que Re(l)>0. Por conveniencia se escoge d=0.08, de manera que al calcular los extremos del espacio de Turing de acuerdo a (26) se obtiene:

(44)

Utilizando un dominio tal que 0 ≤ x ≤ p , de las ecuaciones (33) y (34) se obtiene:

(45)

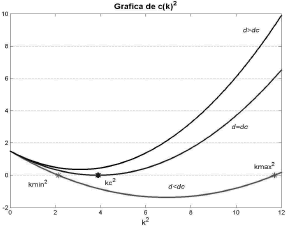
Figura 9. Término c(k²) de la expresión (21) para el modelo de glucólisis
Figure 9. The term c(k²) in the expression (21) for the glycolysis model

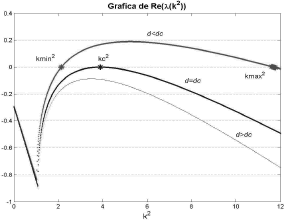
Figura 10. Parte real de los autovalores de (19) para el modelo de glucólisis
Figure 10. Real part of the eigenvalues in (19) for the glycolysis model

Luego, el único valor entero para n es n=2, es decir, un número de onda igual a 2. La figura 11 resume estos resultados. En este caso se omite el resultado para la concentración de v ya que u y v presentan el comportamiento activador-inhibidor observado para el modelo de Schnakenberg. Los parámetros de la simulación son δ=1.2, k=0.06, d=0.08. Se requirieron 50 iteraciones y un paso de tiempo Dt=1. Un análisis similar permite establecer que para δ=2.8 y k=0.06 se obtiene (u₀,v₀)=(0.3544,2.8). Los valores críticos de difusión asociados son d_c=0.0212 y d_c=0.7345. De acuerdo con las figuras 9 y 10, si se hace d=0.0125 y se calcula (26), al desarrollar (33) y (34) teniendo en cuenta que el dominio es tal que 0 ≤ x ≤ p, se obtiene:

(46)

de donde n puede tomar los valores enteros n=4, 5 ó 6. Sin embargo, el número de onda es n=5 ya que representa mayor estabilidad dentro del intervalo dado por (46). La figura 12 corrobora la elección del número de onda. Nuevamente se omite el resultado para la concentración de v ya que u y v presentan el comportamiento activador-inhibidor observado para el modelo de Schnakenberg. Los parámetros de la simulación son δ=2.8, k=0.06, d=0.0125. Se requirieron 100 iteraciones y un paso de tiempo Dt=1.

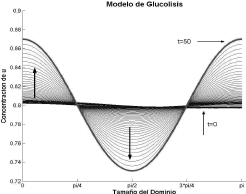
Figura 11. Concentración de u para el modo n=2. Modelo de Glucólisis en 1D
Figure 11. Concentration of u for the mode n=2. Glycolysis model in 1D

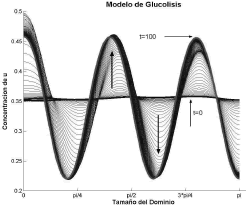
Figura 12. Concentración de u para el modo n=5. Modelo de Glucólisis en 1D
Figure 12. Concentration of u for the mode n=5. Glycolysis model in 1D

Para el caso bidimensional, si se escoge δ=1.75 y k=0.05, se puede verificar mediante el procedimiento mencionado que el modo de onda está dado por la expresión:

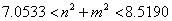(47)

de donde se obtiene nuevamente que los únicos valores enteros que pueden tomar n y m son n=m=2, es decir, el modo (2,2). La simulación de este modo se muestra en la figura 13. En ella, a) y b) son las concentraciones para u y v respectivamente. Las dos imágenes corresponden al tiempo t=5.000. Los parámetros de la simulación son δ=1.75, k=0.05, d=0.0518. Se requirieron 50.000 iteraciones y un paso de tiempo Dt=0.1. La solución se hace sobre una malla de elementos cuadriláteros bilineales de 50 x 50 definida en un dominio de [0,p] x [0,p].

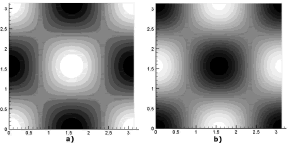
Figura 13. Concentraciones de u y v para el modo (2,2). Modelo de Glucólisis en 2D
Figure 13. Concentrations of u and v for the mode (2,2). Glycolysis model in 2D

Un segundo resultado se obtiene si se elige δ=2,8 y k=0.06, en cuyo caso el modo de onda asociado está dado por la expresión:

(48)

de donde m=2 y n=5, es decir, un modo de onda (2,5).

La simulación de este modo se muestra en la figura 14. En ella, a) y b) son las concentraciones para u y v respectivamente. Las dos imágenes corresponden al tiempo t=3.000. Los parámetros de la simulación son δ=2,8, k=0.06, d=0.0125. Se requirieron 30.000 iteraciones y un paso de tiempo Dt=0.1. Se utilizó una malla de elementos cuadriláteros bilineales de 50 x 50 definida en un dominio de [0,p] x [0,p].

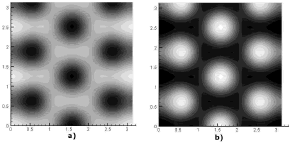
Figura 14. Concentraciones de u y v para el modo (2,5). Modelo de Glucólisis en 2D
Figure 14. Concentrations of u and v for the mode (2,5). Glycolysis model in 2D

 

5. DISCUSIÓN

Los modelos matemáticos utilizados demuestran que las ecuaciones de reacción difusión son de utilidad para representar la formación de patrones en sistemas biológicos [2, 11]. Se evidencia la existencia de inestabilidades espaciales debido a pequeñas perturbaciones del estado estacionario uniforme, y la relación entre estas inestabilidades y los parámetros de cada modelo [1, 2, 4, 9].

El espacio de Turing es el espacio numérico donde el conjunto de parámetros de un modelo cumple las condiciones dadas en (25) y es posible la formación de patrones espacio-temporales [9, 10]. En las figuras 1, 2, 9 y 10 se recurrió a un método matemático basado en la formulación de (19) [12, 15] que permitió obtener los parámetros adecuados para la formación de patrones espacio temporales en los modelos de Schnakenberg y glucólisis. Por su parte, la obtención del número de onda a partir de las expresiones (26) y (34) permite predecir la distribución de los patrones espaciales que se forman con los parámetros elegidos. Esto se evidencia en las figuras 3-6 y 11-12, todas exhibiendo el patrón especificado por el número de onda asociado.

El análisis matemático presentado hace posible la extensión del método predictivo a problemas de mayor dimensión [2]. En el caso unidimensional, la formación del patrón a partir del número de onda asociado es de fácil seguimiento si se evalúa el número de medio ciclos que traza la solución. Esto se explica por el carácter de función par que posee el coseno que resulta en la solución dada por (16) [2]. Para el caso bidimensional, la traza de la solución debe cumplir el número de medio ciclos en los bordes de dominio, conforme a lo expresado por (29). Las figuras 3-6 y 11-12 dan evidencia de lo anterior para el caso unidimensional, mientras que las figuras 7, 8, 13 y 14 respaldan la predicción para el caso bidimensional.

A partir del desarrollo de la expresión (34) se encontró que existe la posibilidad de tener más de un número de onda para un mismo conjunto de parámetros. La razón de esto es la distancia existente entre las raíces del espacio de Turing definidas por (26) y la magnitud del valor de difusión determinado por los valores de las raíces de (28). Una mayor distancia entre el valor de difusión elegido y el valor de difusión crítico, amplia el espacio de Turing y permite que exista más de un número entero en el intervalo definido por (34) [12, 15]. Sin embargo, y aunque sea posible más de un número de onda con un conjunto de parámetros dado, la formación del patrón corresponderá al de aquel número de onda que represente mayor estabilidad al sistema, esto es, al número de onda que se encuentre más cerca de la media geométrica entre las raíces de (26). Este hecho particular se analiza para el modelo de glucólisis con los parámetros δ=2.8, k=0.06, d=0.0125, valores que conducen a un espacio de Turing con tres números de onda válidos, a saber n=4, 5, y 6. La figura 12 muestra que el patrón espacial responde al número de onda más estable, en este caso, n=5.

La implementación de los modelos dados por (1) y (2) mediante el método numérico de los elementos finitos permite reproducir los resultados obtenidos por otros métodos reportados [1, 2, 6, 11]. La técnica empleada proporciona una solución a problemas complejos que requiere de menor costo computacional y permite obtener una mejor aproximación numérica, siempre que el dominio, el mallado y las características temporales sean bien especificados [2]. De esta manera, se espera que la técnica de solución empleada, en conjunto con el análisis matemático de estabilidad, sean de utilidad en la formulación e implementación de modelos matemáticos biológicos complejos que describan fenómenos de crecimiento y desarrollo celular y tisular.

 

REFERENCIAS

[1] MAINI, P. K. Mathematical models in morphogenesis. En: Mathematics Inspired by Biology. Springer Berlin- Heidelberg, 151-189, 1999.         [ Links ]
[2] GARZÓN, D. A. Simulación de procesos de reacción-difusión: aplicación a la morfogénesis del tejido óseo [Tesis de Doctorado]. Zaragoza, España: Centro Politécnico Superior de la Universidad de Zaragoza. 2007.         [ Links ]
[3] DOLNIK, M., A. M. ZHABOTINSKY, A. B. ROVINSKY, I. R. EPSTEIN. Spatio-temporal patterns in a reaction-diffusion system with wave instability. Chemical Engineering Science 55 (2), 223-231, 2000.         [ Links ]
[4] BENSON, D, P. K. MAINI, J. A. SHERRATT. Unravelling the Turing bifurcation using spatially varying diffusion coefficients. J. Math. Biol. 37,381-417, 1998.         [ Links ]
[5] MAINI, P. K. Using mathematical models to help understand biological pattern formation. C. R. Biologies 327, 225-234, 2004.         [ Links ]
[6] MAINI, P. K., K. PAINTER, H. CHAU. Spatial pattern formation in chemical and biological systems. J. Chem. Soc., Faraday Trans. 93 (20), 3601-3610, 1997.         [ Links ]
[7] WANG, Z., T. LI, S. RUAN. Travelling wave fronts in reaction-diffusion systems with spatio-temporal delays. J. Differential Equations 222, 185-232, 2006.         [ Links ]
[8] TURING, A. M. The chemical basis of morphogenesis. Philos. Trans. Roy. Soc. 237, 37-72, 1952.         [ Links ]
[9] MURRAY, J. D. Mathematical Biology II. Spatial models and biomedical applications. Springer-Verlag, 1993.         [ Links ]
[10] PAGE, K., P. K. MAINI, N. MONK. Patter formation in spatially heterogeneous Turin reaction-diffusion models. Physics D. 181, 80-101, 2003.         [ Links ]
[11] PAINTER, K. J. Chemotaxis as a mechanisms for morphogenesis [PhD Thesis]. United Kingdom: Oxfod University, 1997.         [ Links ]
[12] MADZVAMUSE, A. A numerical approach to the study of spatial pattern formation. [PhD Thesis]. Oxford, UK: Computing Laboratory.University of Oxford, 2000.         [ Links ]
[13] ZILL, D. G. Ecuaciones diferenciales con aplicaciones de modelado. Thomson, México, 1997.         [ Links ]
[14] MURRAY, J. D. Mathematical Biology I. An introduction. Springer-Verlag, 2001.         [ Links ]
[15] CRAMPIN, E. Reaction diffusion patterns on growing domains [PhD Thesis]. Oxford, UK: Magdalen College. University of Oxford, 2000.         [ Links ]
[16] HUNTER, P. FEM/BEM Notes. Departament of Engineering Science. The University of Auckland, New Zealand . 2001.         [ Links ]
[17] OÑATE, E., J. MIQUEL, F. ZÁRATE. Stabilized solution of the multidimensional advection–diffusion–absorption equation using linear finite elements. Computers and Fluids 36, 92–112, 2007.         [ Links ]
[18] OÑATE, E. Cálculo de estructuras por el Método de los Elementos Finitos. CIMNE, España, 1992.         [ Links ]