Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.77 n.161 Medellín jan./mar. 2010
STABILITY ANALYSES OF FOOTWALL SLOPES IN OPEN PIT MINING
ANÁLISIS DE ESTABILIDAD DE TALUDES DE MURO EN EXPLOTACIONES MINERAS A CIELO ABIERTO
LEANDRO R. ALEJANO
Departamento de Ingeniería de los Recursos Naturales y Medio Ambiente, Universidad de Vigo, España, alejano@uvigo.es
ABEL SÁNCHEZ JUNCAL
Departamento de Ingeniería de los Recursos Naturales y Medio Ambiente, Universidad de Vigo, España
Received for review May 20th, 2009, accepted December 6th, 2009, final version December 17th, 2009
ABSTRACT: In this paper we analyse different failure mechanisms typically associated to footwall slopes, in order to evaluate its stability using the numeric code UDEC. These results will then be analysed and contrasted against the Limit Equilibrium Method (LEM) to determine the use of UDEC as a valid tool in footwall slope analysis. Two real cases, where the footwall slope failure took place through complex mechanisms, are finally analysed using UDEC.
KEYWORDS: Rock engineering, Stability analyses, Footwall slope, UDEC.
RESUMEN: En éste artículo se analizan diferentes mecanismos de rotura típicamente asociados a taludes de muro, con el objetivo de poder evaluar su estabilidad, mediante el código numérico UDEC (Código de Elementos Distintos Universal). Se analizan, también, mediante métodos de equilibrio límite (MEL), comparándose los resultados obtenidos por ambos métodos, a fin de determinar la validez del código UDEC como herramienta de análisis de la estabilidad de taludes de muro. Se incluye además, el análisis de dos casos reales, en los que la rotura del talud se produjo por mecanismos complejos.
PALABRAS CLAVE: Mecánica de rocas, Análisis de estabilidad, Taludes de muro, UDEC.
1. INTRODUCTION
In mineral deposits associated with sedimentary rock, the economic limit is commonly defined by the footwall of the deeper seam to be mined. Where open pit mines are developed in dipping strata, a high footwall slope may result, which is usually designed with an angle equal or less steep than that of the bedding planes to avoid planar failure (see Figure. 1).
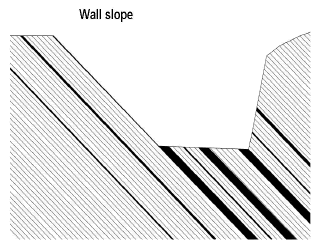
Figure 1. Typical footwall slope where the instabilities analyzed in this study may take place
This design is sometimes appropriate, but some failure mechanisms -associated with bedding planes or any other persistent discontinuity parallel to the slope- may occur producing undesirable instability effects, whose study is the object of this paper.
These types of phenomena do not only take place in sedimentary rock –where they are more common (see for instance Coulthard et al. [1] or Hawley et al. [2]) – but it has also been observed in metamorphic rocks like slate –whenever a slope is designed parallel to cleavage– and in any type of opencast seam mining in which behind the footwall slope any persistent discontinuity or weak material is encountered.
This last case has been reported for instance, in the case study of a quartz mine [3] and in the case study of the Brenda Mine, where clay gouge zones induced wall slope instabilities in a quartz diorite host rock [4].
These instability mechanisms are not very often considered in classic civil or mining rock slope design techniques. However, they have produced some important accidents in mines. They are mainly linked to the sliding of a mass of rock through one of these pre-existing discontinuities, but they also need either one or more smaller discontinuities, or the yield of an area of intact rock due to compressive, shear or tensile stress to allow toe breakout.
In classic rock mechanics literature and in practice, these types of phenomena were studied by means of standard Limit Equilibrium Methods (LEM). However, presently and due to the advances in numerical modeling, distinct element codes, such as UDEC [5], have shown to be a useful tool to understand the mechanism associated with these phenomena and to calculate the safety factor of the designed footwall slope, based on the shear strength reduction technique [6]. The numerical approach to study these problems was firstly introduced by Stead and Eberhardt [7]
2. METHODOLOGY
We have analysed different problems with different footwall slope failure mechanisms. A factor of safety (FoS) can be estimated for these mechanisms according to limit equilibrium methods (LEM) [8]. This FoS can also be calculated according to the shear strength reduction technique (SSRT) and by means of numerical models. For the failure modes where discontinuities play a significant role, it is very appropriate to use distinct element codes such as UDEC [5].
A numerical model simulates reality as it is. In this way, if one models a slope, either it is stable or it falls. Therefore, in order to obtain a FoS with numerical models, we need to use special techniques, such as the SSRT. This technique estimates the factors of safety (FoS) by performing a series of models with different tentative values of the FoS. These tentative values are used to reduce the actual values of the strength properties of the rock and joints (cohesion, friction, tensile strength), until the instability of the slope is observed. The final value of the FoS according to the SSRT is that corresponding to a limiting state (equilibrium-instability).
In this paper, we present a series of simple cases of possible footwall slope failures. We will analyse them by means of LEM. Then they will be studied by means of the UDEC-SSRT.
3. FAILURE MECHANISMS OBSERVED
High slopes with persistent discontinuities parallel to the slope face are prone to fail according to different mechanisms, reviewed by Hawley et al. [2] and can be primarily divided according to the full or partial discontinuity control. If the failure mechanism is totally controlled by pre-existing discontinuities, the instability phenomena presented in the next section may take place. If no secondary joints -enabling instability- exist, then, the discontinuity control is only partial and the failure phenomena necessitating the crushing or shearing of the rock mass. The instability mechanisms resulting in this case are geometrically similar to the previously mentioned ones, but they are obviously less likely to occur.
3.1 Totally joint controlled failure mechanisms
The most commonly encountered mechanisms, presented in Figure 2 include:
- Bilinear slab failure, which involves sliding along a basal plane in combination with sliding along a secondary shallow dipping joint, which is undercut by the slope face (Fig. 2.A). In reference [2] this type of failure is reported in a mine.
- Ploughing slab failure, which takes place when slab sliding along a primary discontinuity combines with sliding along a joint, which strikes sub-parallel to the slope face, causing the toe block to be lifted by sliding and eventually rotated out of the slope (Fig. 2.B). Although this mechanism is not very common Ramírez-Oyanguren [9] reported various cases, where this type of failure was observed.
- Three hinge buckling, described by Cavers [10], is the third known mechanism of this type. It assumes the presence of at least three joints normal to bedding in the slopes lower part. Failure is initiated when enough water pressure exists in the basal plane to induce rotation or shearing along cross-joints causing the extrusion of blocks. (Fig. 2.C).
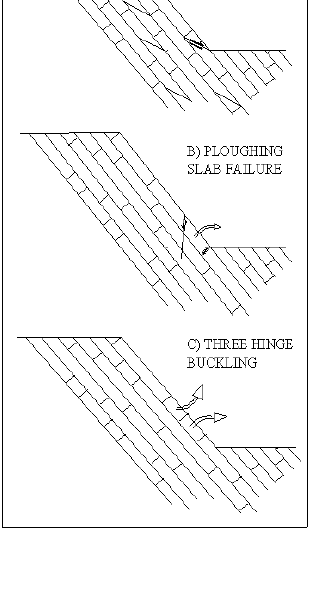
Figure 2. Totally discontinuity controlled failure mechanisms observed on footwall slopes, including A) Bilinear slab failure, B) Ploughing slab failure and C) Three hinge buckling
There are other kinematically possible failure modes but they have not been reported or observed as far as the authors are concerned.
3.2 Partially joint controlled failure mechanisms
The three basic mechanisms of this type analogous to those fully controlled by discontinuities and presented in Figure 3 are:
- Bilinear slab failure with shearing and/or crushing in the toe of the slope, similar to the one all along discontinuities, but with the failure of the rock mass penetrating through the slope toe. Recently Fisher [10] has studied in detail these mechanisms.
- Ploughing slab failure, with shearing of the rock mass in the slope face and shearing or tensile separation in the toe of the slope.
- Euler buckling of the first rock bed as presented by Cavers [11].

Figure 3. Partially discontinuity controlled failure mechanisms observed on footwall slopes, including A) Bilinear slab failure with shearing, B) Ploughing slab failure with shearing and tensile failure and C) Euler buckling
Due to the higher strength of the rock mass versus the rock joints, these mechanisms are much less common than the previously presented ones, but they should not be a priori discarded in a design analysis.
4. LIMIT EQUILIBRIUM METHODS
LEMs are based on the force and moment equilibrium in a rock mass or in different sliding or toppling blocks in a mass. The method may require some more or less realistic assumptions be made. The degree of realism of these hypotheses determines the reliability of the results obtained. If, as in the case of fully discontinuity controlled cases, failure is due to movements of blocks fully limited by geological discontinuities, the geometry and joint shear strength are the key parameters in the analyses and, when no untrue assumptions are taken, LEM are accurate enough to obtain reliable results.
4.1 Discontinuity controlled bilinear slab failure
The stability analysis is done dividing the sliding elements into an active block (1) or slab and a passive block (2) in the toe (Figure 4). For the sake of simplicity, the calculations that follow assume null cohesion joints and no underground water.
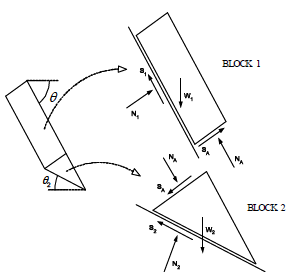
Figure 4. Bilinear slab failure analysis geometry
First, the normal external force needed by the active block to be stable (NA) is calculated, and then, this force is transferred to the resisting block to calculate the safety factor. The analysis needs an assumption concerning the state of the interface between the active and the resisting blocks. If we assume that this boundary is frictionless, it can be found that:
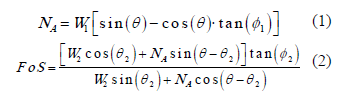
If we assume that there is friction acting on this interface, and that the upper block is in limit equilibrium, it can be found that:
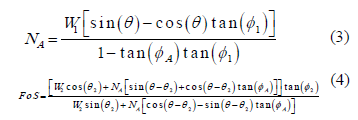
The realism of these assumptions varies according to the case, so no one can be considered a priori better. However, the actual value of the factor of safety has to be one in-between the values obtained according to the presented hypothesis. According to our experience, we suggest for practice the use of the average value safety factor (frictionless and friction assumptions).
4.2 Discontinuity controlled ploughing slab failure
The method of analysis is similar to the bilinear slab failure (see Figure 5). But in this case two further topics should be considered in greater detail.
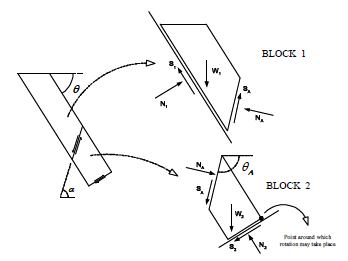
Figure 5. Ploughing slab failure analysis geometry
First, the only kinematically available possibility for the resisting block to move involves that the interface in-between blocks should be in limit equilibrium, so the second assumption proposed for the previous case should not only be used, but it is also a highly realistic one.
Second, the passive block may move out of the slope by either sliding through the upper and lower limiting discontinuities or rotating freely out of the toe of the slope. It turns out then, that a different factor of safety should be computed for both types of mechanisms, finally selecting the smaller FoS, which will also mark the type of behaviour to be expected.
Assuming friction acting on the interface, we find:
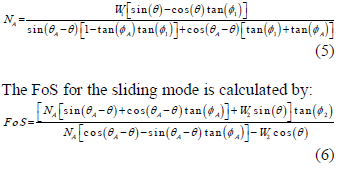
For the limit equilibrium of the toppling case, some geometric values are needed, which are defined in Figure 6. Finally, the FoS for the toppling mode is:
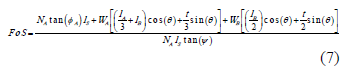
Where:
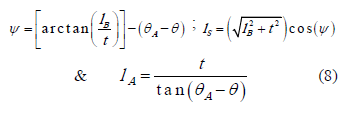
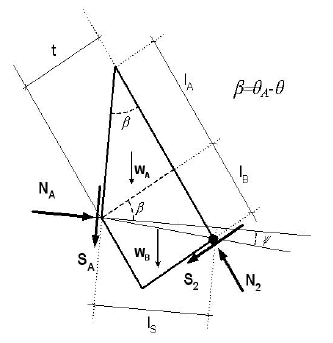
Figure 6. Detail of block 2 for the toppling analysis
5. THEORETICAL EXAMPLES
To deepen the understanding on these mechanisms some theoretical examples are analysed according to LEM and numerical model (UDEC) and the SSRT. Another goal is to contrast these techniques and highlight their advantages and draw-backs. The examples concern totally joint controlled mechanisms –for which only rigid blocks are needed–.
5.1 Example 1. Bilinear slab failure
The analysis focuses on a 50 m slope, dipping 50º (q =50º), formed by 3 m strata (t=3 m), and with a joint striking parallel to the slope in its toe and dipping q 2=30º. The example includes another joint normal to bedding and located as shown in Figure 4. The friction angle of bedding is f 1 = 30º and that of the other joints is fA = f2 = 40º. The specific weight for examples 1 to 5 is g = 25 kN/m3. Under these circumstances and applying LEM and UDEC & SSRT, the results are shown in Table 1.
Table 1. Factors of safety for the proposed examples 1, 2 & 3
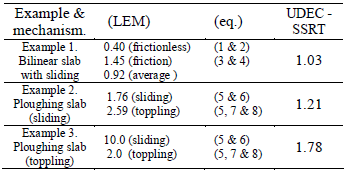
It can be checked that in the interface there is not only normal force –frictionless model–, but also shear one which is smaller than that needed to produce the movement of blocks along this interface –friction LEM–. Then it seems, that even if a shear force appears, it is smaller than that needed for limit equilibrium, so the FoS will be smaller than that obtained for that case, but larger than the frictionless one. The factors of safety obtained by means of UDEC-SRRT are usually not far from the average (friction-frictionless) LEM value.
5.2 Example 2. Ploughing slab failure (sliding)
The analysis studies a 25 m slope, dipping 50º (q=50º), formed by 1.5 m strata (t=1.5m), and with a joint striking parallel to the slope in its toe and dipping towards the slope with 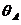 =95º, according to Figure 5. There is also a joint normal to bedding passing through the slope toe. For bedding planes
=95º, according to Figure 5. There is also a joint normal to bedding passing through the slope toe. For bedding planes 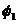 =30º and for the rest of the joints f A = f 2 =20º. The distance so called
=30º and for the rest of the joints f A = f 2 =20º. The distance so called 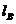 in Figure 6 is
in Figure 6 is 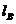 =2.293m.
=2.293m.
The results are shown in Table 1. A lower value of the FoS is obtained for the sliding case than for the toppling case. This can be read in terms of the mechanism of instability, which should be sliding. Also the in the analysis with UDEC and the SSRT a sliding mechanism is observed. However the accurateness of the obtained figures is not very good.
5.3 Example 3. Ploughing slab failure (toppling)
The study focuses a 25 m slope, dipping 60º ( 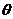 =60º), formed by 1.5 m beds (t=1.5 m), and with a joint striking parallel to the slope in its toe and dipping towards it, with
=60º), formed by 1.5 m beds (t=1.5 m), and with a joint striking parallel to the slope in its toe and dipping towards it, with 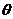 A=95º. There is also a joint normal to bedding in the slope toe and
A=95º. There is also a joint normal to bedding in the slope toe and 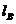 =3 m. The friction of bedding planes is
=3 m. The friction of bedding planes is 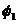 = 30º and for the rest of the joints
= 30º and for the rest of the joints 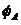 =
= 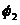 = 40º.
= 40º.
The results are shown in Table 1. In this case LEM and UDEC-SRRT compare well, for they both indicate toppling failure, and the FoS values are similar in both cases. Figure 7 shows the UDEC mechanisms of examples 1 to 3.
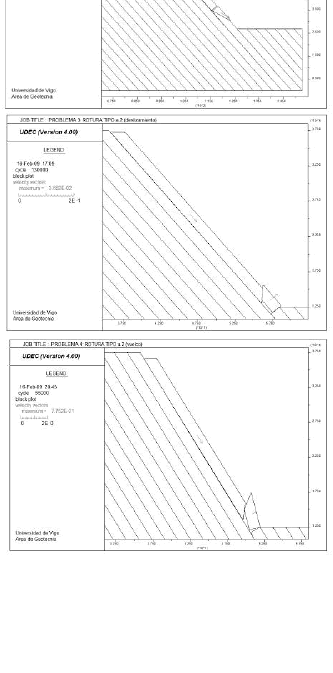
Figure 7. UDEC response of examples 1 to 3, where the different mechanisms can be observed
One can be surprised at the differences in FoS obtained by both methods. In the case of example 1, this is due to the fact that neither the frictionless nor the friction assumptions are strictly correct. In examples 2 and 3, this can be due to the following: every factor of safety compares two figures, one related to the forces or moments tending to stability and the other related to those tending to instability. Since the approaches are different, they must only coincide for the case of limit equilibrium (FoS =1,00) and they can diverge as long as the FoS is far from 1. FoS is not an actual variable, but it is an indicative value of the risk engineers are ready to assume. This is studied in the next examples.
5.4 Examples 4 and 5. Ploughing slab failure
We analyse two examples, 4 and 5, representative of the failure mechanisms of ploughing slab failure, with sliding and toppling of the resisting block respectively. In both of them, the LEM FoS obtained is 1.00, -that is to say- they are in limit equilibrium. The results of the analysis are shown in Table 2.
Table 2. Factors of safety for the proposed examples 4 & 5
For the case of sliding (example 4) the safety factor obtained by UDEC and the SSRT is exactly 1.00, demonstrating the accurateness of both methods to detect limit equilibrium.
However, for the case of toppling (example 5), even if the FoS is close to one, it differs in 0.1 unities. This inaccurate result was surprising, so we investigated the possible reasons. We finally found out that this was due to the roundness of the corners of the UDEC blocks. The program selects a small value of this roundness automatically. When changing this value to a very small one (r= 0.0005 m), the FoS for toppling in example 5 became 0,9994, and then, practically 1.00. So it can now be stated that, when performing very detailed geometrical models and close to limit equilibrium, both techniques (LEM & UDEC-SRRT), yield the same response.
6. PRACTICAL CASE STUDIES
Two real cases studies are briefly presented. In both cases the LEM approach is not easy, since not only one but various strata were involved in the failure processes. Therefore, an approach based on numerical models (UDEC) is preferred in order to understand the evolution of the instability mechanisms, which took place.
6.1 Case study 1
We study the instability of slope occurred during the excavation of a highway in northern Spain . This case was presented in detail by some authors [12]. The geometric description of the slope is shown in Figure 8.
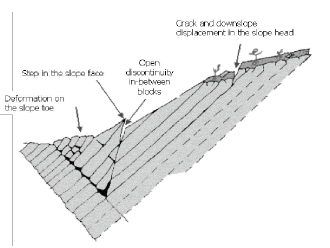
Figure 8. Geometry and identified features of a wall slope failure in road according to [12]
The instability was finally caused by the water pressure after a very rainy period. A detail of the upper part of the slope is illustrated in Figure 9.

Figure 9. Picture of the tension crack in the upper part of the slope
The UDEC analysis determined that the dry slope was stable, whereas the inclusion of water induced the instability. The failure mechanisms as derived from our UDEC approach is illustrated in Figure 10.
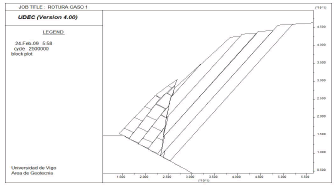
Figure 10. UDEC mechanism of the failure of a wall slope failure as developed by the authors
6.2 Case study 2
An outstanding footwall slope failure took place in Leigh Creek open pit coal mine in Australia . The original study of the topic was developed by Coulthard et al. [1], which can be consulted for further details on the case study.
The LEM analyses determined that the slope was a stable one. Nevertheless, when the slope attained a depth of 100 meters as shown in Figure 11 the slope failed. Ten very weak 1 m thick strata slided through a very weak bedding plane located 10 m below the slope face.

Figure 11. Picture of the footwall slope failure in Leigh Creek mine
The UDEC model is able to determine the instability of this slope only partially controlled by discontinuities. The failure mechanism is shown in Figure 12, where it is observed how the toe breakout needs shearing of the rock mass. This topic of the analysis of biplanar dip slope failures to limit model and parameter uncertainty in the determination of setback distances has been addresses in detail by Fisher [10].
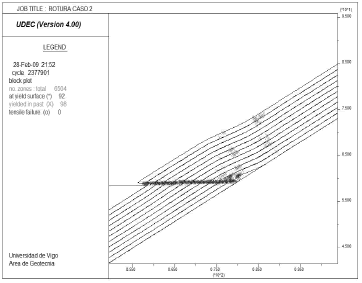
Figure 12. Detail of the UDEC model showing the shearing of the rock in the base of the slope failure in Leigh Creek mine. Remark that shearing of the rock mass is required for toe breakout
According to this case it is clear that very complex mechanisms are difficult to analyse by means of LEM, and a tool such as UDEC can be very helpful for understanding and identifying wall slope failure mechanisms in actual case studies, as well as to study its possible evolution.
7. CONCLUSIONS
Footwall slope failure mechanisms have been reviewed and different techniques –LEM and the SSRT with code UDEC– to obtain factors of safety in these cases have been presented and applied to various examples and two case studies. As a consequence of all this, the following considerations have been drawn.
LEM are a good choice to obtain FoS in those footwall slopes where the failure mechanism grants limit equilibrium in all blocks –ploughing slab failure with sliding or toppling of the resisting block–. For the case of full discontinuity controlled bilinear slab failure results are not sufficiently good and more realistic assumptions are needed. The role of friction could be further investigated by analysing practical cases or by means of physical modelling. This topic is a present research line of the authors.
The partially discontinuity controlled bilinear failure mechanism requires shearing through the rock mass or along a discontinuity above the toe. Therefore, the frictionless model proposed by Hawley et al. [2] is really not appropriate for theses cases. This is illustrated in Figure 12. These failure mechanisms are complex and needs shear failure through the rock mass. Fischer [10] provides an interesting discussion on the topic, which falls out of the scope of this study.
LEM, if results are reliable, are preferred than SSRT in that it is easier to perform further –but commonly needed– analysis like parametric studies, back-analysis, statistical analysis like Monte Carlo and so on.
The combination of the SSRT with UDEC is a very strong technique to estimate FoS for every mechanism of footwall slope instability, having the advantages of finding automatic and naturally the failure mechanism and the critical slip or separation surfaces. It should be used within the frame of more wide design methodology as proposed by Starfield & Cundall [13], that is to say as a tool for thinking and understanding mechanisms, more than a calculating machine.
Nevertheless, this technique is more complex to use; making more difficult the carrying out of further studies.
8. ACKNOWLEDGEMENTS
The authors acknowledge local Government of Galicia (Consellería de Innovación e Industria de la Xunta de Galicia ) the financing received to develop this research project under the title Stability analysis of wall slopes, with reference number (INCITE08PXIB304076PR).
REFERENCES
[1] COULTHARD, M.A., LUCAS D.S. AND FULLER, P.G. Application of UDEC to a stress-related mine slope failure al Leigh Creek, South Australia. Proceedings of the Symposium on Numerical Modelling of Discrete Materials, Bochum ( Germany ). Ed. Konietzky. Balkema. Pp. 289-296. October 2004. [ Links ]
[2] HAWLEY P.M, MARTIN, D.C. & ACOTT. C.P. Failure mechanics and design considerations for footwall slopes. 87th Ann. Gen. Meet. Can. Inst. of Min. & Metall. Vancouver. 29 pp. 1985. [ Links ]
[3] ALEJANO, L.R.; GARCÍA BASTANTE, F., ALONSO, E. & GÓMEZ-MÁRQUEZ, I. Stability analysis and design of two quarry slopes with the help of numerical modeling. EUROCK 2001, ISRM Symposium, Rock Mechanics a challenge for society. Espoo, Finland . Ed. Balkema. June, 2001. [ Links ]
[4] CALDER, P.N.. AND BLACKWEL, G.H.. Investigation of a complex rock displacement at Brenda Mines. The Canadian Mining and Metallurgy Bulletin. Pp. 1-10. August, 1980. [ Links ]
[5] ITASCA. 2000. User manual for UDEC, Version 3.1. Itasca Consulting Group Inc., Minnesota, USA . [ Links ]
[6] DAWSON, E.M., ROTH, W.H. & DRESCHER, A. Slope stability analysis by Strength reduction. Geotechnique. 49(6): 835-840, 1999. [ Links ]
[7] STEAD, D., EBERHARDT, E. Developments in the analysis of footwall slopes in surface coal mining. Engineering Geology 46: 41-61. 1997. [ Links ]
[8] RAMÍREZ OYANGUREN, P. & ALEJANO, L.R. Numerical and Analytical stability analysis of footwall slopes in opencast coalmines. Geotech. Meet. Santiago de Chile (Chile). September, 1992. [ Links ]
[9] RAMÍREZ OYANGUREN, P. 2003. Personal communication. [ Links ]
[10] FISHER, B.R. Improved characterization and analysis of biplanar dip slope failures to limit model and parameter uncertainty in the determination of setback distances. [PhD Thesis] . Vancouver, British Columbia, Canada : University of British Columbia, 2009. Available: https://circle.ubc.ca/handle/2429/11559. [Visited 15 December 2009] . [ Links ]
[11] CAVERS, D.S. Simple methods to analyse buckling of rock slopes. Rock Mech. & Rock Eng. 14: 87-104, 1981. [ Links ]
[12] MANERA BASSA, C.; RAMÍREZ OYANGUREN, P. Rotura en dos bloques de los taludes de muro de explotaciones de carbón. Boletín Geológico y Minero. Volumen 99. 261-266, 1986. [ Links ]
[13] STARFIELD, A.M. & CUNDALL, P.A. Towards a methodology for rock mechanics modelling. Int. J. of Rock Mech. Min. Sci. & Geom. Abstr. 25(3): 99-106, 1988. [ Links ]














