Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.77 n.162 Medellín abr./jun. 2010
UN MODELO POSIBILÍSTICO PARA ESTIMAR EL COSTO INTRÍNSECO DE LA ENERGÍA NO SUMINISTRADA EN SISTEMAS DE DISTRIBUCIÓN ELÉCTRICA
A POSSIBILISTIC MODEL TO ESTIMATE THE INTRINSIC COST OF NON SUPPLY ENERGY IN ELECTRIC DISTRIBUTION SYSTEMS
GUSTAVO SCHWEICKARDT
Investigador del CONICET, Argentina. Instituto de Economía Energética, Fundación Bariloche gustavoschweickardt@ciudad.com.ar
HÉCTOR PISTONESI
Instituto de Economía Energética, Fundación Bariloche. e-mail: hpistone@criba.edu.ar
Recibido para revisar Junio 8 de 2009, aceptado Febrero 1 de 2009, versión final Marzo 3 de 2010
RESUMEN: En el presente trabajo se desarrolla un novedoso modelo para estimar el costo de la energía no suministrada en sistemas de distribución de energía eléctrica. Se propone un enfoque multi-objetivo y flexible, sustentado en programación dinámica posibilística, reconociendo en cada criterio de optimización identificado, la existencia de incertidumbres no estocásticas de valor. El costo resultante, por no ser fijado externamente y depender de la estructura modelo-representación del sistema, se designa como intrínseco. El modelo se centra en la ubicación óptima de equipos de seccionamiento y protección, aspecto de mayor impacto en el diseño confiable. Se comparan, sobre un mismo sistema real, sus resultados respecto de los obtenidos por un método basado en programación dinámica determinística, en la que el costo en cuestión es fijado regulatoriamente. Se evidencian las ventajas de la optimización posibilística respecto del enfoque clásico determinístico.
PALABRAS CLAVE: Distribución Eléctrica, Energía No Suministrada, Optimización, Conjuntos Difusos.
ABSTRACT: In the this work a new model to estimate the non supply energy costs in electric distribution systems, is presented. A multi-objective and flexible approach, based in possibilistic dynamic programming, is proposed, recognizing, for each optimization criteria, the existence of non stocastic incertainties. The resulting cost is not externally defined and depends only on the structure model-representation of system; then it's designed as intrinsic cost. The strategy proposed has been developed to defines the location and optimal number of sectionalizing devices. The proposed model is compared with a classic method supported in deterministic dynamic programming, applied on the same real system, and the advantages for the possibilistic approach are evidenced.
KEYWORDS: Electric Distribution, Non Supply Energy, Optimization, Fuzzy Sets.
1. INTRODUCCIÓN
El diseño de los sistemas de protección en los Sistemas de Distribución de Energía Eléctrica (SDEE), se ha sustentado, históricamente, en exigencias operativas. Las soluciones se han formalizado en términos de la experiencia de los planificadores (reglas de buena práctica) [1].
En los últimos años, la reforma eléctrica es aplicada al segmento de distribución. Comienzan a exigirse, desde los cuerpos regulatorios, determinados índices de confiabilidad (continuidad del suministro) teóricamente fundados en la maximización del beneficio de los agentes que integran el sistema (monopolista-distribuidor y clientes). Desde este enfoque, el problema de diseño pasa a ser de naturaleza económica. Esto supone que deberán ser satisfechos dos requisitos inherentes a un problema de optimización: a) debe requerirse el mínimo conjunto de factores en la prestación del servicio de distribución eléctrica, aspecto vinculado a la eficiencia productiva y b) tales factores, deben valorizarse según su costo social de oportunidad, aspecto vinculado con la denominada eficiencia asignativa. El segundo punto, constituye un problema de dificultosa solución, puesto que, no obstante la regulación fije valores monetarios, no se conoce, y mucho menos determinísticamente, cuánto cuestan a la sociedad los efectos de la interrupción del suministro eléctrico.
2. GENERALIDADES SOBRE EL PROBLEMA DE LA CONFIABILIDAD DE LOS SDEE
2.1 Índices de Confiabilidad
Para integrar el objetivo confiabilidad como criterio de decisión a optimizar, se supone que la misma ha sido valorizada en términos de un costo económico. Existen diversos índices. En [2] son diferenciados dos grupos: aquellos basados en el número de clientes y aquellos basados en la energía. En este trabajo, serán utilizados tres índices basados en clientes y uno basado en energía. Son definidos a continuación:
A) Índice de Frecuencia de Interrupciones Promedio del Sistema (System Average Interruption Frequency Index) SAIFI:
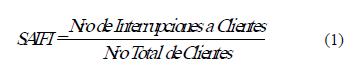
B) Índice de Duración de las Interrupciones Promedio del Sistema (System Average Interruption Duration Index) SAIDI:
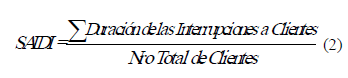
C) Índice de Frecuencias de Interrupciones Transitorias Promedio (Momentary Average Interruption Frequency Index) MAIFI:

D) Energía No Suministrada (Non Supply Energy) ENS (sigla en castellano):

donde: Pi representa la potencia en el nodo i-ésimo del sistema con nN nodos, [kVA], que ha sido interrumpida por un tiempo ti, [h].
Este valor puede resultar referido a otro período (por ejemplo semestral); luego, debe ser anualizado. Como es desconocido (esperado) su cálculo requiere de una estimación. Según el método empleado en la misma, los valores resultantes para este indicador pueden diferir. De modo que, conjuntamente con el valor del índice, debe ser especificada con claridad la metodología empleada en el cálculo.
Nótese que los cuatro índices adoptados, responden a las características deseables al ponderar las interrupciones: su frecuencia (SAIFI), su duración (SAIDI) y su ENS, si la interrupción no es transitoria. Para interrupciones transitorias, interesa su frecuencia (MAIFI).
En el contexto del modelo propuesto, el problema estriba en determinar si los valores económicos conferibles a tales índices, resultan aceptables para un sistema confiable. Específicamente, interesa la ENS.
2.2 Ubicación Óptima de Equipos de seccionamiento y protección (sp) en un alimentador ideal
Considérese un alimentador ideal, representado en la Figura 1, en el cual se procura instalar un equipo de seccionamiento/protección (sp). Exhibe las siguientes características: a) una distribución uniforme de cargas, (p), en su longitud; b) una tasa de falla (l) uniforme por unidad de longitud y c) un tiempo medio de reparación de falla (tr), constante. Adicionalmente, se supondrá: 1) que el tiempo que requiere el equipo para ser accionado (tiempo de maniobra, tm), es conocido y 2) que en la salida del alimentador se encuentra instalado un equipo, sp.
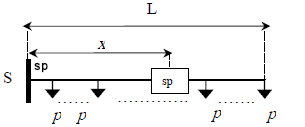
Figura 1. Ubicación de un equipo sp en un alimentador ideal
Figure 1. Location of a sp device in an ideal feeder
Se emplea un criterio de minimización de la ENS, definida mediante:

donde: P es la potencia media interrumpida, [kW] y l la longitud del tramo interrumpido, [km]; l se expresa en [fallas/km x año] y tr se expresa en [h], de modo que ENS se expresará en [kWh/año]. x refiere la ubicación óptima del equipo sp, y es la distancia medida desde el nodo de salida; L es la longitud total del alimentador ideal.
Tal criterio conduce a la expresión:
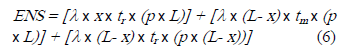
donde: el primer corchete, representa la ENS debido a fallas ocurridas entre la salida del alimentador y el equipo sp, y que afectan sólo a los usuarios en dicho tramo hasta que la falla se repare (tr); el segundo corchete representa la ENS por fallas ocurridas aguas abajo de sp, que afectan a todos los usuarios, hasta que transcurra tm y se aísle el tramo correspondiente por accionamiento de sp; y el tercer corchete representa la ENS que afecta a los usuarios aguas abajo de sp, hasta la reparación de la falla (tr).
Si se deriva ENS(x) y se iguala a cero (condición de primer orden para existencia de extremo, mínimo, dado el problema), se tiene:
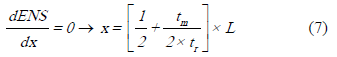
y considerando que: tm << tr → x ≈ L/2.
Si se pretendiesen ubicar dos equipos sp, sus localizaciones óptimas x e y, se aproximarían a x = y = L/3. Como regla general, puede inferirse que: para un alimentador ideal con una distribución de carga uniforme, los equipos sp deberán instalarse también uniformemente, siempre que tm << tr.
2.3 Caracterización del Problema de Optimización de la Confiabilidad por la Ubicación de Equipos sp
Los sistemas con alimentadores reales, se alejan considerablemente de las hipótesis ideales. En un alimentador real, puede decirse que: a) las cargas se concentran en nodos y tienen valores muy diferentes; b) la topología del alimentador exhibe tramos con distintos entornos, que modifican el valor de la tasa de fallas; c) la condición tm << tr no necesariamente se cumple y, si se trata de redes aéreas, d) los tiempos de reparación, pueden ser diferentes según las características geográficas y climáticas de la zona.
Desde tales consideraciones, la caracterización del problema de ubicación óptima de equipos sp se puede presentar en los siguientes términos: a) Es multi-objetivo y restricto, dominado por un conjunto de incertidumbres, muchas de las cuales no son de naturaleza estocástica (por caso: demanda, precio de la energía, costos y fundamentalmente, incertidumbres de valor sobre los objetivos y los límites fijados a las restricciones) y b) Requiere de una optimización combinatoria, cuya función(es) objetivo(s) es(son) no lineal(es) y no diferenciable(s). El número de estados, NE, del espacio de búsqueda, cuando se trata de ubicar óptimamente un conjunto de nsp equipos en un alimentador radial, con N tramos o secciones, resulta:
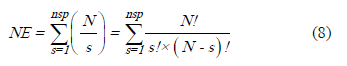
3. UBICACIÓN DE EQUIPOS SP CUANDO EL COSTO DE LA ENS ES EXTERNAMENTE FIJADO
3.1 Enfoque mono-objetivo según la Maximización de Beneficios
Este enfoque se sustenta en la consideración de los beneficios obtenidos al minimizar la ENS. Se asumen condiciones determinísticas (no existen incertidumbres). La localización óptima de los equipos sp puede ser resuelta mediante la comparación entre los beneficios para cada posible alternativa de ubicación.
Para obtener una expresión del beneficio referido, considérese lo siguiente: a) Si no existen equipos sp en el alimentador, cualquier falla causará la interrupción del suministro a todos los clientes abastecidos, durante el tiempo que tarde la reparación, (tr); b) Si existe un equipo sp, entonces cualquier falla aguas abajo de su localización, ocasionará la interrupción del suministro a los clientes aguas arriba, sólo durante un tiempo igual al tiempo de aislación (de la falla) o maniobra, (tm) y c) Existe un costo unitario, fijado externamente, para la energía no suministrada. El beneficio asociado a la instalación de un equipo sp en el tramo i-ésimo del alimentador, podrá expresarse conforme los siguientes pasos:
Si td es la tasa de descuento anual asociada al costo de capital de un equipo sp, cuyo costo es CEqSP y cuya vida útil es nvu, entonces el factor de recuperación de capital, viene dado por:
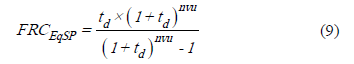
Así, la anualidad de la inversión del equipamiento sp, [US$/año], resulta:
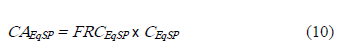
y adoptando un porcentaje, p%, del costo de inversión anual en concepto de costo de operación y mantenimiento del equipo sp:
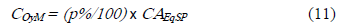
entonces el beneficio, [US$/año], por instalar el equipo sp en el tramo ti, será:
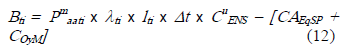
donde: Pmaati es la demanda media, [kW], totalizada aguas arriba del tramo ti (interumpida durante tm [h]); lti es la tasa de falla anual por unidad de longitud, [fallas/km x año], del tramo ti; lti es la longitud del alimentador aguas abajo del tramo ti, [km]; Δt = tr - tm es la diferencia entre el tiempo de reparación y el de aislamiento de la falla, [h]; CuENS es el costo unitario de la energía no suministrada, [US$/kWh]. El beneficio es obtenido mediante la valorización de la energía no suministrada desde la potencia no interrumpida, Pmaati, en el tiempo de reparación de la falla, tr, según el costo CuENS. Es decir que se pondera el ahorro por no haberse interrumpido la potencia aguas arriba de ti, durante el tiempo tr, gracias a la instalación del equipo sp.
3.2 Aplicación de la programación dinamica clasica (PD)
La Programación Dinámica (PD) clásica o determinística, se sustenta en el principio de optimalidad de Bellman [3]. Requiere considerar el problema abordado, como un proceso de decisión multi-etapa, en el cual la política óptima es determinada recursivamente. Puede ser enunciado como sigue: para N etapas, la transición que arroja el valor óptimo de la función f, f*, mediante una función de transición, gtr, entre cada par (estado, etapa), (i, k-1) a (j, k), resulta:
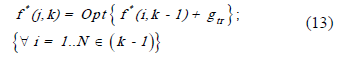
Si f es Bti, los requerimientos para resolver el problema mediante PD, son satisfechos desde las siguientes consideraciones: a) El problema puede ser dividido en etapas. En cada una se plantea la ubicación de un equipo sp individualmente; b) Cada etapa, tendrá un número de estados, que se corresponderán con los tramos del alimentador en donde es posible instalar un equipo sp; c) La función de transición, gtr, entre el estado i de la etapa k-1, (i, k-1) al estado j de la etapa k, (j, k) (dinámica hacia delante), resultará del beneficio adicional, dado por (12), obtenido al instalar un equipo sp en el tramo j; d) La particularidad de este enfoque, es que, a priori, el número de etapas N resulta desconocido. Sin embargo, se tienen dos características del problema que permiten definir N dinámicamente. Asumiendo funciones contínuas, sin pérdida de generalidad, puede aseverarse que: d-1) La función ENS(k) ≡ ENS(nsp), calculada por extensión de (6), es decreciente (con k o nsp), siendo nsp el número de equipos sp ubicados. Por tanto, a medida que se incrementa nsp, el ahorro por disminución de la ENS será menor; d-2) La función de costo en concepto de inversión y operación y mantenimiento CA(k) ≡ CA(nsp), es creciente (con k o nsp). De aquí que la función dinámica de beneficio a partir de (12), exhiba un valor extremo (máximo) para 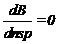 . Por lo tanto, cuando por efecto de la dinámica propuesta, la función de beneficio resulte en un valor menor en la etapa k, respecto del obtenido en k-1, entonces se asigna N = k-1 y se detiene el procedimiento. N resultará la etapa de máximo beneficio, al cual corresponde el número de equipos sp ubicados. La política óptima se reconstruye recursivamente.
. Por lo tanto, cuando por efecto de la dinámica propuesta, la función de beneficio resulte en un valor menor en la etapa k, respecto del obtenido en k-1, entonces se asigna N = k-1 y se detiene el procedimiento. N resultará la etapa de máximo beneficio, al cual corresponde el número de equipos sp ubicados. La política óptima se reconstruye recursivamente.
4. MODELO FLEXIBLE BASADO EN PROGRAMACIÓN DINÁMICA DIFUSA/ POSIBILÍSTICA (PDD/PDP)
4.1 Formulación general del modelo restricto
En el contexto propuesto, para un alimentador real en Media Tensión (MT), al optimizar la confiabilidad del sistema mediante la ubicación de equipos sp, se adopta la formulación siguiente (integrando a la ENS, los indicadores de frecuencia y duración de fallas permanentes, y de fallas transitorias, según se presentó en el epígrafe 2.1):

El grupo 2.- de restricciones se supone, para el modelo, satisfecho. Cada variable tiene la interpretación dada en espresiones anteriores; CENS es el costo en [US$] de la ENS. Los valores límites de los indices de confiabilidad, son definidos por la autoridad regulatoria. Puede plantearse una modelación alternativa, cuando no se dispone del costo unitario imputable a la ENS. Para ello se elimina el término CENS en la función objetivo, y se agrega en el grupo 1.- una restricción de valor máximo, ENS ≤ ENSlim.
En cualquiera de estos modelos, existe el problema de la valoración, monetaria, en caso de la ENS, y técnico/económica (límites aceptables), cuando se trata de los índices. Específicamente, en la regulación argentina, se asigna como penalización un costo unitario a la ENS, CuENS, para el cual nada garantiza que represente un costo social de oportunidad (costo económico) asociado a la continuidad del suministro eléctrico.
4.2 La PDD bajo conjuntos difusos normales y convexos para los objetivos restricciones dinamica posibilistica PDP
La Programación Dinámica Difusa, supone una extensión del principio de optimalidad de Bellman, que gobierna la política óptima en la PD, al dominio difuso. Para ello se considera el principio de optimalidad de Bellman-Zadeh [4], aplicable a decisiones estáticas valuadas en conjuntos difusos. Puede sintetizarse mediante las siguientes consideraciones:
1) Un conjunto difuso de la variable u, es definido mediante una función, denominada función de pertenencia. La misma adopta un valor máximo para el valor más posible, (verosímil o satisfactorio), y mínimo (cero), para los valores menos posibles. Se dice que el conjunto es normal, si el máximo valor de pertenencia es 1, para un único valor de u.
2) Sea un sistema con un conjunto de Objetivos Difusos {O} = {O1, O2,., On}, valuados mediante funciones de pertenencia μOj, j=1..n, con un vector de variables de decisión [X] = {x1, x2 ,..., xD } y con un vector de variables de estado [Y] = {y1, y2 ,..., yE }.
{O} se encuentra sujeto a un conjunto de Restricciones Difusas {R} ={R1, R2,., Rh}, valuadas mediante funciones de pertenencia μRi, con i=1..h.
Entonces el Conjunto Difuso de Decisión, D, se define como:
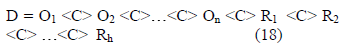
siendo <C> un operador llamado, en general, de confluencia entre los conjuntos. Su correlato entre las funciones de pertenencia respectivas, se indicará mediante C. Un operador típico, lo constituye la intersección: <C> ≡ ∩, y su correlato entre las funciones de pertenencia, es el operador min (mínimo de los valores de las funciones de pertenencia, en la instancia de decisión).
3) Los objetivos y restricciones del problema son, entonces, relajados y representados por conjuntos difusos, conforme (18). A los efectos de que los mismos resulten comparables, se procede del siguiente modo: si el objetivo considerado es Oj y se tiene un contexto de minimización, se adopta un valor de referencia máximo (RefMax) y un valor de referencia mínimo (RefMin). A partir de éstos se compone la función μ(Oj) (función de pertenencia del conjunto) tal que adopte el valor 1 (máxima pertenencia o aceptación) si Oj ≤ RefMin y el valor 0 (mínima pertenencia o aceptación) si Oj ≥ RefMax. Idénticamente, se procede con las restricciones. Lo mismo, invirtiendo los valores {0, 1}, resulta para un contexto de maximización. Luego, extendiendo (18) a las funciones de pertenencia así obtenidas, la decisión estática maximizante, en el conjunto de variables de decisión [X], sobre cierto conjunto de alternativas [A], resultará:
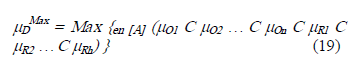
En cuanto al operador C, se emplea una función t, denominada t-norma, definida en el intervalo [0, 1] aplicado también en [0, 1], la cual satisface las siguientes condiciones:
Si t: [0, 1] → [0, 1] es una t-norma, entonces:a.- t(0,0) = 0; t(x,1) = x - Condiciones de Frontera; b.- t(x,y) = t(y,x) - Conmutatividad; c.- si x ≤ α e y ≤ β 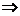 t(x,y) ≤ t(α,β) - Monotonicidad; d.- t((t(x,y),z) = t(x,t(y,z)) - Asociatividad.
t(x,y) ≤ t(α,β) - Monotonicidad; d.- t((t(x,y),z) = t(x,t(y,z)) - Asociatividad.
Según 3), las funciones de pertenecia serán normales. Sus conjuntos difusos, convexos, son distribuciones de posibilidades [5]. Se plantea, entonces, el principio de optimalidad de Bellman-Zadeh, que gobierna la PDD, para resultar en una dinámica posibilística (PDP). Se presenta a continuación.
4.3 La PDP aplicada al problema específico
Combinando (13) y (19), la dinámica posibilística propuesta para el modelo, basándose en [6], [7] y [8], se formulará:
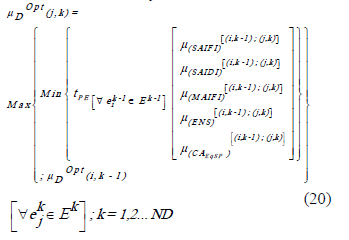
Es decir: el criterio para arribar del modo más satisfactorio a cierto estado de la etapa k, es el de (19): μDMax = Max { tPE { (μ(SAIFI); μ(SAIDI); μ(MAIFI); μ(ENS); μ(CAEqSP)} }, donde el operador C ≡ tPE. tPE es una t-norma que será explicada seguidamente. La decición maximizante dinámica, μDOpt, se obtiene si la decisión maximizante estática se extiende entre cada estado 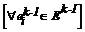 y cada estado
y cada estado 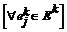 , donde
, donde 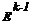 y
y 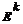 son los vectores de estado (cuyas componentes son t-uplas(SAIFI, SAIDI, MAIFI, ENS, CAEqSP)) de las etapas k-1 y k, respectivamente, con k=1, 2 . ND. ND resulta, como se explicó, un número dinámico de etapas, pues, a priori, no es conocido. Para determinarlo, debe definirse cómo es conducida esta dinámica. Para ello, deberán desarrollarse, primeramente, las funciones de pertenencia.
son los vectores de estado (cuyas componentes son t-uplas(SAIFI, SAIDI, MAIFI, ENS, CAEqSP)) de las etapas k-1 y k, respectivamente, con k=1, 2 . ND. ND resulta, como se explicó, un número dinámico de etapas, pues, a priori, no es conocido. Para determinarlo, debe definirse cómo es conducida esta dinámica. Para ello, deberán desarrollarse, primeramente, las funciones de pertenencia.
4.4 Las Funciones de Pertenencia definidas para el Modelo Posibilístico
Para los conjuntos difusos solidarios a los índices basados en clientes se propone lo siguiente: a) Existen valores límites, fijados por regulación, por debajo de los cuales no se aplica penalización alguna. Entonces se adopta como índice de mayor satisfacción, el valor resultante de decrementar el límite impuesto, un porcentaje pI% (cualquier valor mayor que el así establecido, tendrá aceptación máxima también):
IMin =ILim x (1-pI%/100); b) Se adopta como índice de menor satisfacción, cierto valor IMax, que surge de simular su cálculo, por definición, sin instalar ningún equipo sp en el alimentador (excepto el ubicado en la salida); c) Se construye un conjunto difuso cuya función de pertenencia es lineal, a partir de estos dos valores extremos (IMin e IMax); d) Se establece una escala de preferencias entre todos los índices de confiabilidad, la ENS y el (CAEqSP+COyM), la cual arroja ponderadores exponenciales, pExpC, de los conjuntos difusos [8]. Estos ponderadores afectan al conjunto contrayéndolo, si pExpC >1 o expandiéndolo, si pExpC < 1. La contracción aumenta la importancia del criterio afectado, mientras que la expansión la disminuye.
Este efecto, sobre una función de pertenencia lineal de variable genérica u, puede apreciarse en la Figura 2. Los ponderadores exponenciales, constituyen una forma adicional de enfatizar las incertidumbres de valor sobre los criterios del sistema. En el caso del conjunto difuso solidario al índice ENS, se procede también a una construcción lineal de su función de pertenencia, ponderada exponencialmente.
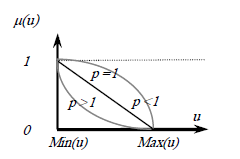
Figura 2. Contracción (p>1) y expansión (p<1) de un conjunto difuso lineal (p=1)
Figure 2. Contration (p>1) and expansion (p<1) of a linear fuzzy set (p=1)
Sus valores máximo y mínimo de satisfacción son obtenidos como sigue: a) ENSmax resulta de calcular la ENS en las mismas condiciones que las fijadas en el item b) para los índices de confiabilidad basados en clientes; b) ENSmin resulta de calcular la ENS en una condición tal que todos los tramos del alimentador tengan instalado un equipo, no redundante, sp. Esta consideración sobre la ENSmin supone también una consideración sobre el costo máximo en equipamiento, tales que fijan una referencia, razonable, a la que todos los usuarios podrían aspirar. Imponer un valor cero como ENSmin no tiene correlato razonable en el costo de inversión requerido.
Por último, para obtener la función de pertenencia del conjunto difuso solidario al costo de inversion (incluyendo el de operación y mantenimiento) de los equipos sp, se procede del siguiente modo: a) Se tiene un CAEqSPMIN correspondiente a la situación en que se determina ENSmax, que resultará nulo ya que no se instala ningún equipo sp; b) Se adoptará un CAEqSPMAX que corresponde a la condición de ENSmin. Luego, la función lineal obtenida se pondera exponencialmente.De modo que, si se refiere cada uno de los cinco criterios como Crit, su valores máximo y mínimo como CritMax y CritMin, y su ponderador exponencial como pμ(Crit), se tiene como expresión general para las funciones de pertenencia:
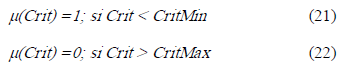
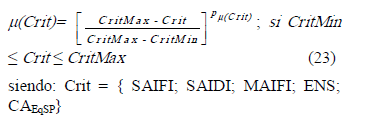
4.5 Operador de confluencia t-norma producto de Einstein (tpE)
Para el modelo propuesto, el operador de confluencia más adecuado resultó ser la t-norma denominada Producto de Einstein, definida como:
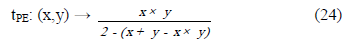
donde x e y son dos funciones de pertenencia genéricas, de las definidas en 4.4.
La construcción utilizada en (20), en virtud de la propiedad asociativa de una t-norma, se obtiene mediante los siguientes pasos:
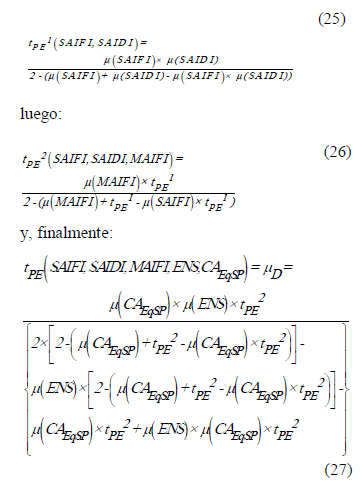
dependiente de 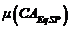 y
y 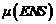 .Tal dependencia no es casual. Tiene que ver con el próximo elemento a introducir en el modelo, para la conducción de su dinámica.
.Tal dependencia no es casual. Tiene que ver con el próximo elemento a introducir en el modelo, para la conducción de su dinámica.
5. CONDUCCIÓN DE LA PDP MEDIANTE LA INTRODUCCIÓN DEL COSTO INTRÍNSECO DE LA ENS
Para cierto nivel de satisfacción, 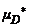 , desde (27) se obtiene:
, desde (27) se obtiene:
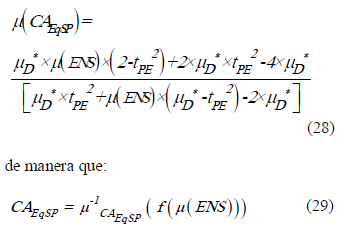
Se intenta encontrar, bajo la hipótesis 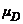 =
= 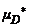 , una expresión que relacione los cambios diferenciales en el CAEqSP cuando se producen cambios diferenciales en la ENS. Se obtiene de este modo:
, una expresión que relacione los cambios diferenciales en el CAEqSP cuando se producen cambios diferenciales en la ENS. Se obtiene de este modo:
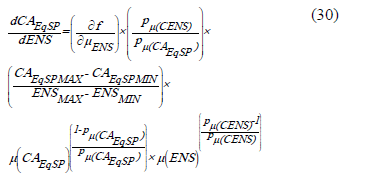
La expresión (30) resulta negativa, porque 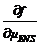 lo será. Tiene la forma de un costo
lo será. Tiene la forma de un costo
marginal de la ENS. Puede interpretarse como el incremento de costo de la última unidad de calidad producida ≡ no calidad no producida. Por otro lado, este costo no es fijado externamente de manera directa, sino que dependerá de la estructura datos-representación del modelo propuesto. Se lo designará como Costo Intrínseco de la Energía No Suministrada. Su expresión será:
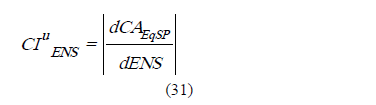
El beneficio que permitirá conducir la optimización dinámica, resultará, desde la expresiones (12) y (31):
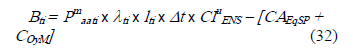
Siendo 1,2.j los tramos del alimentador en el cual se instala un equipo sp, en cada etapa e = 1..k, la condición de salida k = ND, será:

A diferencia del enfoque PD, el beneficio no siempre es positivo, puesto que el CIuENS se irá reduciendo a medida que se ubiquen más equipos sp. El valor CIu(ND)ENS, previo a alcanzar la condición (33), se referirá como Costo Intrínseco Residual, CIu(res)ENS. El mismo podría resultar en una penalización regulatoria, en concepto de la ENS.
6. SIMULACIÓN
En la Figura 3, se representa el esquema unifilar de una salida real desde una Estación Transformadora 33/13.2 [kV]. Pertenece al SDEE de San Carlos de Bariloche, Río Negro Argentina. La configuración corresponde al año 2000. Existe un único interruptor, ubicado a la salida del alimentador principal, de la Estación, indicado como Is.
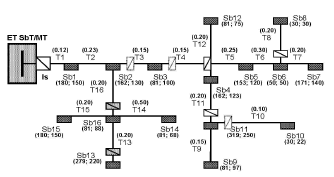
Figura 3. Esquema Unifilar del Alimentador MT
Figure 3. Unifilar Scheme of MV Feeder
La simulación pretende comparar los resultados entre los dos modelos presentados. En la parte superior de cada tramo (Ti) se indica su longitud en [km]. En la parte inferior de cada centro de transformación media/baja tensión (Sbi) se indica el par (Potencia [kVA]; Nro de Clientes). Se ha considerado un factor de potencia de 0.95; para los equipos sp: costo = 10000 US$, vida util = 15 años y tasa de descuento td = 12%; los tiempos de maniobra y reparación de la falla son tm = 1 [h] y tr = 4 [h]; la tasa de falla se ha considerado constante, l = 0.32 [fallas/año-km]. El costo regulatorio de la ENS, se fijó en 2 [US$/kWh]. Resultaron: SAIFImin = 0.95, SAIFImax = 2; SAIDImin = 1 [h], SAIDImax = 3 [h]; MAIFImin = 0.45; MAIFImax = 1. Para la ENS, resultaron los valores límites: ENSmin = 500 [kWh/año], ENSmax = 1023.17 [kWh/año]; y para los equipos sp: CAEqSPMIN = 0, CAEqSPMax = 21000 [US$/año]. Se omitirá en las unidades, la referencia [año]. El vector de ponderadores resultó:
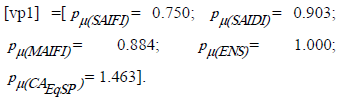
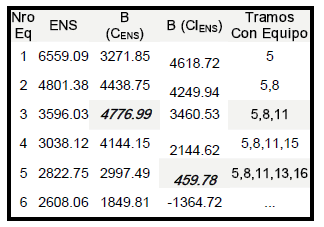
La Tabla 1 presenta los resultados para ambos modelos. En PD, ND=3 y en PDP, ND=5. En negrita se indica el beneficio de salida y los sp ubicados. En la Figura 3, se indican los sp ubicados, con rectángulos en línea llena (y una diagonal), más oscuros para la PD.
Tabla 1. Comparación entre los equipos ubicados según el Modelo PD y el Modelo PDP
Table 1. Comparison between sp devices located as results of Models PD and PDP
La evolución del CIuENS, resultó:
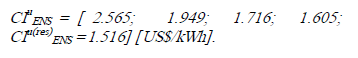
Al modificar el vector de ponderadores según: [vp2] =[ 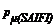 = 0.750;
= 0.750; 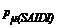 = 0.545;
= 0.545; 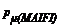 = 0.470;
= 0.470; 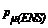 = 2.000;
= 2.000; 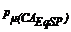 = 1.235], dando más importancia a
= 1.235], dando más importancia a
la ENS, el Modelo Posibilístico (el Determinístico no se modifica): ubica 3 equipos más, en los tramos 4, 3 y 10 de la Figura 3 (rectángulos con línea diagonal y de puntos). Resulta (ND = 8 Etapas):
Vector de Evolución de la ENS [kWh]:
ENS = [6559.1; 4801.4; 596.0; 3038.1;
2822.8; 2608.1; 2464.1; 2350.3]
Vector de Evolución de los Beneficios [US$]:
B = [11431.5; 11329.8; 11133.5; 10024.5; 8176.6; 6088.9; 3638.3; 890.4]
Vector de Evolución del CIuENS [US$/ kWh]:
CIuENS = [5.254; 3.854; 3.371; 3.160; 2.988; 2.782; 2.550; CIu(res)ENS = 2.280]
6. CONCLUSIONES
1) Se presentaron dos modelos para la Optimización de la Confiabilidad de los SDEE (en MT), focalizándose en la ubicación óptima de equipos sp. El 1er modelo, se basa en Programación Dinámica Clásica, conducida por el Beneficio valorizado al Costo de la ENS impuesto regulatoriamente. El 2do modelo, se sustenta en Programación Dinámica Posibilística, conducida por un Costo de la Energía No suministrada, consecuencia de las propiedades del modelo. Por ello es referido como Costo Intrínseco de la ENS.
2) Al introducir esta medida intríseca de conducción en la Optimización Posibilística, se intenta propiciar la valoración económica de un criterio, la ENS, conocida sólo por imposición regulatoria. Como se desprende de los desarrollos presentados, la manera en que se mide la importancia de la continuidad del suministro, incorpora un conjunto de subjetividades que pueden captarse por diversos mecanismos. Este es el caso de los ponderadores, las incertidumbres de valor (modeladas mediante conjuntos difusos), y el operador de confluencia. La tPE, es una muy buena opción, pero pueden ser exploradas otras, guardando coherencia metodológica en los resultados vinculados al CIuENS.
3) Según [vp1], CAEqSP es más importante que ENS; igualmente se logra una confiabilidad mayor que por valoración regulatoria. [vp2] aumenta la confiabilidad al conferir más importancia a ENS que a CAEqSP. Este es un efecto metodológicamente coherente.
REFERENCIAS
[1] Lakervi E., Holmes E. Electricity Distribution Network Design. IEE Power Engineering Series 21, 2nd Edition, London, United Kingdom , 1999. [ Links ]
[2] Institute of electrical and electronics engineers. IEEE Guide for Electric Power Distribution Reliability Indices, Std 1366TM, 2003. [ Links ]
[3] BELLMAN R. and Dreyfus E. Applied Dynamic Programming. Princeton University Press, 1962. [ Links ]
[4] Bellman, R. and Zadeh, L. Decision-Making in a Fuzzy Environment. Management Science, 17, pp. 141-164, (1970). [ Links ]
[5] Doubois D., Prade H. Fuzzy Sets and Systems: Theory and Applications. New York, London, Toronto Press, 1980. [ Links ]
[6] García E., Schweickardt G., and Andreoni A. A New Model to Evaluate the Dynamic Adaptation of an Electric Distribution System. Energy Economics. ELSEVIER. Vol. 30, issue 4 pp. 1648-1658, 2008. [ Links ]
[7] Schweickardt G., Miranda V. A Two-Stage Planning and Control Model Toward Economically Adapted Power Distribution Systems using Analytical Hierarchy Processes and Fuzzy Optimization. International Journal of Electrical Power & Energy Systems. ELSEVIER. Vol. 31, issue 6 pp. 277-284, 2009. [ Links ]
[8] Schweickardt G., Miranda V. Un Modelo De Planificación y Control Orientado a La Adaptación Económica de Sistemas de Distribución de Energía Eléctrica. Revista EPIO. Universidad Nacional del Centro, Tandil, Argentina. Nro. 28, pp. 30-49, 2007. [ Links ]














