Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.77 n.162 Medellín abr./jun. 2010
LA TEORÍA DE LOS CONJUNTOS APROXIMADOS PARA EL DESCUBRIMIENTO DE CONOCIMIENTO
ROUGH SETS THEORY TO KNOWLEDGE DISCOVERY
YAILÉ CABALLERO
Departamento de Computación. Universidad de Camagüey, Cuba . yailec@yahoo.com
RAFAEL BELLO
Departamento de Computación. Universidad Central de Las Villas, Cuba. rbellop@uclv.edu.cu
LETICIA ARCO
Departamento de Computación. Universidad Central de Las Villas, Cuba
BEITMANTT CÁRDENAS
Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. beitmantt@yahoo.com
YENNELY MÁRQUEZ
Departamento de Computación. Universidad de Camagüey, Cuba
MARÍA M. GARCÍA
Departamento de Computación. Universidad Central de Las Villas, Cuba
Recibido para revisar Octubre 31 de 2008, aceptado Junio 2 de 2009, versión final Julio 17 de 2009
Resumen: La Teoría de los Conjuntos Aproximados (RST) abrió una nueva dirección en el desarrollo de teorías sobre la información incompleta y es una poderosa herramienta para el análisis de datos. En esta investigación se demuestra la posibilidad de usar esta teoría para generar conocimiento a priori sobre un conjunto de datos. Se desarrolla una propuesta para caracterizar a priori conjuntos de entrenamiento, usando medidas de estimación de la RST. La propuesta ha sido estudiada experimentalmente usando bases de datos internacionales y se han obtenido resultados satisfactorios.
Palabras clave: descubrimiento de conocimiento, Teoría de los Conjuntos Aproximados.
Abstract: The Rough Set Theory (RST) opened a new direction in the development of incomplete information theories and is a powerful tool for the analysis of data. In this investigation the possibility is demonstrated of using this theory to generate knowledge on a data set. A proposal is developed to characterize sets of training, using measures of estimation of the RST. The proposal has been studied experimentally using international data bases and satisfactory results have been obtained.
Keywords: knowledge discovery, Rough Sets Theory.
1. INTRODUCCIÓN
Para los científicos los datos representan observaciones cuidadosamente recogidas de algún fenómeno en estudio; en los negocios, los datos guardan informaciones sobre mercados, competidores y clientes; en procesos industriales, recogen valores sobre el cumplimiento de objetivos. El verdadero valor de los datos radica en la posibilidad de extraer de ellos información útil para la toma de decisiones o la exploración y comprensión de los fenómenos que le dieron lugar [1]. El análisis de datos es importante en ramas como: bioinformática, medicina, economía y finanzas, industria, medio ambiente, entre otras, donde el preprocesamiento de estos es esencial.
Una de las teorías más recientes empleada para el análisis de datos es la Teoría de los Conjuntos Aproximados RST (Rough Set Theory) [2]. Esta teoría se considera como una de las cinco áreas claves y no tradicionales de la Inteligencia Artificial y de la Teoría de la Información Incompleta, pues constituye una herramienta muy útil para el manejo de la información no completa o imprecisa [3].
Los métodos para estudiar la calidad de los conjuntos de entrenamientos (CE) usualmente son aplicados post-aprendizaje, de modo que tienen incluido el costo computacional de aplicar el método de aprendizaje; encontrar métodos que permitan una evaluación a priori del CE es un problema altamente relevante en al área del aprendizaje automatizado.
Como se verá en el presente artículo esta problemática motivó la presente investigación por lo que se dan elementos necesarios en este sentido en el epígrafe 2. Luego, se introducen conceptos importantes acerca de la Teoría de los Conjuntos Aproximados en el epígrafe 3 y posteriormente, en el epígrafe 4 se presenta la propuesta relacionada con el descubrimiento de conocimiento a través de la Teoría de los Conjuntos Aproximados.
2. CARACTERIZACIÓN A PRIORI DE LOS CONJUNTOS DE ENTRENAMIENTO PARA LA CLASIFICACIÓN SUPERVISADA
Usualmente se evalúa la calidad del conocimiento resultante de aplicar algún método de aprendizaje usando el conjunto de control; es decir, la evaluación es post-aprendizaje. A partir de los datos disponibles se aplican diferentes métodos de aprendizaje para determinar cuál produce un mejor conocimiento. El estudio de la relación entre el conjunto de entrenamiento y la eficiencia y eficacia lograda en el proceso de aprendizaje se realiza usando el método de prueba y error de una forma experimental. Es decir, se realizan sucesivos procesos de entrenamiento y se validan los resultados alcanzados. De modo que resulta de gran interés poder estimar la calidad de los datos antes de proceder al aprendizaje para evitar trabajos innecesarios.
Sin embargo, tanto los métodos de aprendizaje como los métodos para mejorar estos conjuntos dependen de la información original contenida en ellos. El estudio de calidad del conjunto de entrenamiento puede servir de base para tomar decisiones sobre cómo desarrollar el aprendizaje. Es decir, dado un conjunto de entrenamiento (training set, TS) se desea tener una función f tal que f(TS) dé un indicador de cuán bueno parece ser TS para extraer desde él conocimiento necesario para construir un clasificador. El problema es encontrar esa función f.
Existen pocos trabajos en este sentido [4, 5, 6, 7, 8]. Uno de ellos es para estimar la calidad, en términos del bias y de la varianza, del conjunto de entrenamiento a través del coeficiente de Bhattacharyya y una distribución gaussiana multivariada. Este trabajo se limita a problemas descritos por dos clases solamente [4]. En 1994, Michie y colaboradores realizan un estudio para estimar, a partir de características de los conjuntos de entrenamiento y medidas estadísticas aplicadas a dichos conjuntos, qué clasificadores supervisados pudieran usarse [5, 6]. Sin embargo, no se obtiene información a priori de la calidad del desempeño de los clasificadores seleccionados. En [8] se realiza un estudio, a partir de las medidas clásicas de los Conjuntos Aproximados, para estimar la calidad de los conjuntos de entrenamiento para redes Perceptron multicapa.
3. LA TEORÍA DE LOS CONJUNTOS APROXIMADOS
La Teoría de Conjuntos Aproximados (Rough Sets Theory) fue introducida por Z. Pawlak en 1982 [2]. Se basa en aproximar cualquier concepto, un subconjunto duro del dominio, como por ejemplo, una clase en un problema de clasificación supervisada, por un par de conjuntos exactos, llamados aproximación inferior y aproximación superior del concepto. Con esta teoría es posible tratar tanto datos cuantitativos como cualitativos, y no se requiere eliminar las inconsistencias previas al análisis; respecto a la información de salida puede ser usada para determinar la relevancia de los atributos, generar las relaciones entre ellos (en forma de reglas), entre otras. La inconsistencia describe una situación en la cual hay dos o más valores en conflicto para ser asignados a una variable [9].
3.1 Principales definiciones de la Teoría de los Conjuntos Aproximados
La filosofía de los conjuntos aproximados se basa en la suposición de que con todo objeto x de un universo U está asociada una cierta cantidad de información (datos y conocimiento), expresado por medio de algunos atributos que describen el objeto [10].
Definición 1. Sistema de Información y sistema de decisiónSea un conjunto de atributos A={a1, a2,…,an} y un conjunto U no vacío llamado universo de ejemplos (objetos, entidades, situaciones o estados) descritos usando los atributos ai; al par (U,A) se le denomina Sistema de información [16]. Si a cada elemento de U se le agrega un nuevo atributo d llamado decisión, indicando la decisión tomada en ese estado o situación, entonces se obtiene un Sistema de decisión (U,A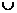 {d}), donde d
{d}), donde d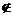 A.
A.
Definición 2. Relación de inseparabilidad
A cada subconjunto de atributos B de A B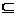 A está asociada una relación binaria de inseparabilidad denotada por R, la cual es el conjunto de pares de objetos que son inseparables uno de otros por esa relación [11].
A está asociada una relación binaria de inseparabilidad denotada por R, la cual es el conjunto de pares de objetos que son inseparables uno de otros por esa relación [11].
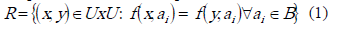
Una relación de inseparabilidad (indiscernibility relation) que sea definida a partir de formar subconjuntos de elementos de U que tienen igual valor para un subconjunto de atributos B de A, B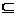 A, es una relación de equivalencia. Los conceptos básicos de la RST son las aproximaciones inferiores y superiores de un subconjunto XÍU. Estos conceptos fueron originalmente introducidos con referencia a una relación de inseparabilidad R. Sea R una relación binaria definida sobre U la cual representa la inseparabilidad, se dice que R(x) significa el conjunto de objetos los cuales son inseparables de x. Así,
A, es una relación de equivalencia. Los conceptos básicos de la RST son las aproximaciones inferiores y superiores de un subconjunto XÍU. Estos conceptos fueron originalmente introducidos con referencia a una relación de inseparabilidad R. Sea R una relación binaria definida sobre U la cual representa la inseparabilidad, se dice que R(x) significa el conjunto de objetos los cuales son inseparables de x. Así, 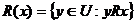 . En la RST clásica, R es definida como una relación de equivalencia; es decir, es una relación binaria R
. En la RST clásica, R es definida como una relación de equivalencia; es decir, es una relación binaria R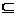 UxU que es reflexiva, simétrica y transitiva. R induce una partición de U en clases de equivalencia correspondiente a R(x), xÎU.
UxU que es reflexiva, simétrica y transitiva. R induce una partición de U en clases de equivalencia correspondiente a R(x), xÎU.
Este enfoque clásico de RST es extendido mediante la aceptación que objetos que no son inseparables pero sí suficientemente cercanos o similares puedan ser agrupados en la misma clase [12]. El objetivo es construir una relación R’ a partir de la relación de inseparabilidad R pero flexibilizando las condiciones originales para la inseparabilidad. Esta flexibilización puede ser realizada de múltiples formas, así como pueden ser dadas varias definiciones posibles de similitud. Existen varias funciones de comparación de atributos (funciones de similitud), las cuales están asociadas al tipo del atributo que se compara. Sin embargo, la relación R’ debe satisfacer algunos requerimientos mínimos. Si R es una relación de inseparabilidad definida en U, R’ es una relación de similitud extendida de R si y solo si 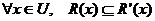 y
y 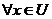 ,
, 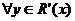 ,
, 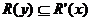 , donde R’(x) es la
, donde R’(x) es la
clase de similitud de x, es decir, R’(x)=
La aproximación de un conjunto XÍU, usando una relación de inseparabilidad R, ha sido inducida como un par de conjuntos llamados aproximaciones R-inferior y R-superior de X. Se considera en esta tesis una definición de aproximaciones más general, la cual maneja cualquier relación reflexiva R’. Las aproximaciones R’-inferior (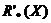 ) y R’-superior (
) y R’-superior (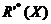 ) de X están definidas respectivamente como se muestra en las expresiones (2) y (3).
) de X están definidas respectivamente como se muestra en las expresiones (2) y (3).
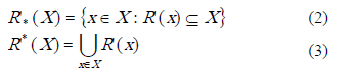
Teniendo en cuenta las expresiones definidas en 2 y 3, se define la región límite de X para la relación R’ [14]:
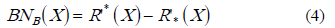
Si el conjunto BNB es vacío entonces el conjunto X es exacto respecto a la relación R’. En caso contrario, 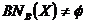 , el conjunto X es inexacto o aproximado con respecto a R’.
, el conjunto X es inexacto o aproximado con respecto a R’.
El uso de relaciones de similitud ofrece mayores posibilidades para la construcción de las aproximaciones; sin embargo, se tiene que pagar por esta mayor flexibilidad, pues es más difícil desde el punto de vista computacional buscar las aproximaciones relevantes en este espacio mayor [15].
Usando las aproximaciones inferior y superior de un concepto X se definen tres regiones para caracterizar el espacio de aproximación: la región positiva que es la aproximación R’-inferior, la región límite que es el conjunto BNB y la región negativa (NEG(X)) que es la diferencia entre el universo y la aproximación R’-superior. Los conjuntos R’*(X) (denotado también como POS(X)), R’*(X), BNB(X) y NEG(X) son las nociones principales de la Teoría de Conjuntos Aproximados.
3.2 Medidas de inferencia clásicas de la Teoría de los Conjuntos Aproximados
La Teoría de los Conjuntos Aproximados ofrece algunas medidas para analizar los sistemas de información. A continuación se muestran las principales. En las expresiones 5 a la 8 se emplean las aproximaciones R’-inferior (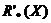 ) y R’-superior (
) y R’-superior (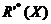 ) de X, las cuales están definidas en las expresiones 2 y 3 respectivamente.
) de X, las cuales están definidas en las expresiones 2 y 3 respectivamente.
Precisión de la aproximación. Un conjunto aproximado X puede ser caracterizado numéricamente por el coeficiente llamado precisión de la aproximación, donde |X| denota la cardinalidad de X, X¹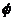 . Observe la expresión (5).
. Observe la expresión (5).

Obviamente, 0£a(X)£1. Si a(X)=1, X es duro (exacto), si a(X)<1, X es aproximado (vago, inexacto), siempre respecto al conjunto de atributos considerado [16].
Calidad de la aproximación. El coeficiente siguiente

expresa la proporción de objetos que pueden ser correctamente clasificados en la clase X. Además, 0 £a(X) £ g (X) £ 1, y g (X) =0 si y solo si a (X)=0, mientras g (X)=1 si y solo si a (X)=1 [16].
Considerando que X1,…,Xl son las clases del sistema de decisión, se define la medida:
Calidad de la clasificación. Este coeficiente describe la inexactitud de las clasificaciones aproximadas:
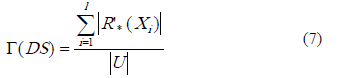
La medida calidad de la clasificación expresa la proporción de objetos que pueden estar correctamente clasificados en el sistema.
Si ese coeficiente es igual a 1, entonces el sistema de decisión es consistente, en otro caso es inconsistente [16].
Función de pertenencia aproximada. Esta función cuantifica el grado de solapamiento relativo entre R’(x) (clase de similitud de x) y la clase a la cual el objeto x pertenece. Se define como sigue:
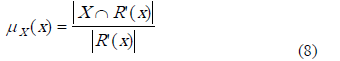
La función de pertenencia aproximada puede ser interpretada como una estimación basada en frecuencias de Pr(xÎX | x, R’(x)), es decir, la probabilidad condicional de que el objeto x pertenezca al conjunto X [17].
4. CARACTERIZACIÓN A PRIORI DE LOS CONJUNTOS DE ENTRENAMIENTO BASADA EN LAS MEDIDAS DE ESTIMACIÓN DE LOS CONJUNTOS APROXIMADOS
En este epígrafe se proponen nuevas medidas de la Teoría de los Conjuntos Aproximados y se desarrolla una propuesta para, a partir de estas, predecir a priori la calidad de un conjunto de entrenamiento, y además poder seleccionar qué tipo de clasificador supervisado será el más conveniente usar en el proceso de aprendizaje: una red neuronal (Perceptron multicapa), un árbol de decisión (C4.5) o un método de aprendizaje perezoso (k-NN).
4.1 Nuevas medidas para evaluar los sistemas de decisión, basadas en la Teoría de los Conjuntos Aproximados.En este epígrafe se proponen variantes generalizadas tanto para la precisión como para la calidad de la clasificación supervisada, porque en muchas aplicaciones los expertos pueden ponderar las clases o se pueden seguir heurísticas para definir en qué medida las clases son importantes.
Precisión generalizada de la clasificación. En esta medida por cada clase se da la posibilidad de considerar un peso que influya en la evaluación del sistema de decisión.
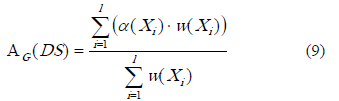
Donde l es la cantidad de clases del sistema de decisión, 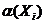 se calcula como se indica en la expresión 5. En la expresión 8 se definió la función de pertenencia aproximada; el cálculo de la media de esta función aplicada a los objetos de la clase, puede ser considerada como una medida de importancia de la clase, es decir, el valor para w(Xi).
se calcula como se indica en la expresión 5. En la expresión 8 se definió la función de pertenencia aproximada; el cálculo de la media de esta función aplicada a los objetos de la clase, puede ser considerada como una medida de importancia de la clase, es decir, el valor para w(Xi).
Calidad generalizada de la clasificación. En esta expresión también se permite ponderar por clases al promediar la calidad de cada aproximación.
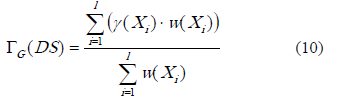
Donde l es la cantidad de clases del sistema de decisión, 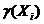 se calcula como se indica en la expresión 8. En [18] se propone la función de compromiso aproximado, esta cuantifica en qué grado la R’(x) (clase de similitud de x) cubre la clase X, y está dada por la expresión 11.
se calcula como se indica en la expresión 8. En [18] se propone la función de compromiso aproximado, esta cuantifica en qué grado la R’(x) (clase de similitud de x) cubre la clase X, y está dada por la expresión 11.
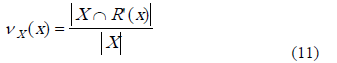
La media del compromiso aproximado de los objetos a la clase, puede ser considerada como un valor para ser asignado al peso de cada clase (w(Xi)), en la expresión 12.
En las expresiones 9 y 10, w(Xi) es el peso de la clase Xi y es un valor entre 0 y 1, este valor puede ser definido por los expertos. El hecho de considerar la media de la pertenencia aproximada y el compromiso aproximado por clases, respectivamente, constituye una manera de dar valor a estos w(Xi).
Resulta interesante no solo considerar los resultados experimentales de medidas que describen a los datos por clases, sino también tener una manera de cuantificar el comportamiento del conjunto de datos de manera general. Por tal motivo, se propone el coeficiente de aproximación general, definido por la expresión 12. Este coeficiente muestra una proporción entre la cantidad de objetos que pudieran ser bien clasificados (aquellos que pertenecen a la aproximación inferior de las clases) y la cantidad de objetos que pudieran o no pertenecer a las clases del sistema de decisión.
Coeficiente de aproximación general. Se evalúa la calidad del sistema de información sin diferenciar por clases.
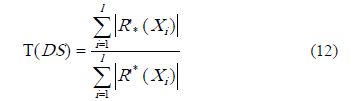
Donde l es la cantidad de clases del sistema de decisión, R’*(Xi) es la aproximación inferior (descrita en la expresión 2) y R’*(Xi) su aproximación superior (descrita en la expresión 3).
4.2 Estudio experimental de la relación entre las medidas de inferencia y el desempeño de los clasificadoresPara el estudio experimental se seleccionaron los conjuntos de datos siguientes: Balance-Scale, Breast-Cancer-Wisconsin, Bupa (Liver Disorders), Dermatology, E-Coli, Heart-Disease (Hungarian), Iris, Lung-Cancer, Monks-1, Pima-Indians-Diabetes, Promoter-Gene-Sequence, Tic-Tac-Toe, Wine Recognition, Yeast, Zoo, Glass, Hayes-Roth, Soybean, Ionosphere, Page-blocks, Postoperative, Waveform, Credit-Screening, Hepatitis y Lymphography.
El esquema siguiente de estudio experimental se aplicó a cada conjunto de datos estudiado:
1. Formación de muestras de entrenamiento y control.
Se obtuvieron los conjuntos de entrenamiento y control, siguiendo el principio de validación cruzada, se selecciona el 75% de los objetos para el entrenamiento y el 25%, para conjunto control.
2. Proceso de clasificación supervisada.
Se realizó el proceso de clasificación supervisada a través de la herramienta Weka, específicamente con los clasificadores supervisados k-Vecinos más Cercanos (IBK), red neuronal Perceptron multicapa y C4.5 (J48).
3. Cálculo de las Medidas de Inferencia.
Para cada conjunto de entrenamiento se calcularon las medidas: Precisión de la aproximación (expresión 5), Calidad de la aproximación (expresión 6), Calidad de la clasificación (expresión 7), Precisión generalizada de la clasificación (expresión 9), Calidad generalizada de la clasificación (expresión 10) y Coeficiente de aproximación general (expresión 12), descritas en los epígrafes 3 y 4. El peso (w(Xi)) que se utilizó para calcular las medidas definidas en las expresiones 9 y 10 fueron la media de la pertenencia aproximada por clases y la media del compromiso aproximado por clases, respectivamente. Se implementó el sistema MIRST1.0 que permite el cálculo de estas medidas de inferencia.
4. Cálculo de correlaciones estadísticas
Con ayuda del SPSS 13.0 se buscan los coeficientes de Correlación de Pearson entre las medidas de inferencia descritas en las expresiones 7, 8 y el desempeño por clases de los clasificadores; así como los coeficientes de correlación entre las medidas descritas en las expresiones 7, 9, 10, 12 y los resultados del desempeño general de la clasificación supervisada. Se llega a coeficientes de correlación en todos los casos cercanos a 1, con una significación bilateral menor que 0.01, con lo que se puede asegurar que el coeficiente de correlación es significativo (p<0.01).
4.3 Generación del conocimiento a partir de las medidas de inferencia usando métodos de aprendizaje automatizado.
Resulta interesante poder inferir conocimiento a partir de estos resultados, es decir, que para un determinado conjunto de entrenamiento, sea posible decidir cuál clasificador supervisado (entre k-NN, MLP y C4.5) es más conveniente aplicar y poder además, dar una valoración cualitativa del resultado de la precisión general que arrojará dicho clasificador para ese conjunto de entrenamiento (baja, media, alta, muy alta). Para esto se ha utilizado el generador de reglas C4.5 y además una red Perceptron multicapa, y se comparan los resultados arrojados por ambos. Además, una vez que se haya seleccionado el clasificador supervisado idóneo para un conjunto de entrenamiento determinado, se puede inferir el valor de su precisión, a través del método estimador de funciones k-Vecinos más Cercanos (k-NN).
Construcción de conjuntos de datos para el entrenamientoPara esto se crearon seis nuevos conjuntos de datos, dos correspondientes a cada clasificador supervisado estudiado: un conjunto de datos con los valores de la precisión discretizados y otro con los valores numéricos de la precisión. Estos conjuntos de datos tendrán cuatro atributos predictores, representados por las medidas: Calidad de la clasificación, Precisión generalizada de la clasificación, Calidad generalizada de la clasificación y Coeficiente de Aproximación General, todos con valores entre cero y uno. El atributo objetivo (clase), para los tres conjuntos de datos con la precisión discretizada, tendrá los valores:
A->"No aplicable, precisión muy baja”
B->"Aplicable, precisión baja”
C->"Aplicable, precisión media”
D->"Aplicable, precisión alta”
E->"Aplicable, precisión muy alta”
Para poder categorizar la precisión de los clasificadores del estudio en A, B, C, D y E, se calcularon los percentiles de la precisión de cada clasificador a través del SPSS 13.0. De esta manera se asociaron los valores de la precisión a las diferentes categorías según:
A->valores inferiores al 20 percentil
B->valores entre el 20 y 40 percentil
C->valores entre el 40 y 60 percentil
D->valores entre el 60 y 80 percentil
E->valores mayores que el 80 percentil
Aquí se pueden aplicar otras técnicas de discretización para categorizar la precisión del clasificador en A, B, C, D, E, por ejemplo el método de dicretización basado en la entropía, discretización basada en el error [19].
Se construyeron los conjuntos de datos a partir de los resultados de las medidas de inferencia y la precisión de los clasificadores. Cada conjunto de datos está formado por 250 ejemplos, pues a cada uno de los 25 conjuntos de datos con los cuales se realizó el estudio, se le dividió aleatoriamente en diez muestras de entrenamiento y prueba.
Generación de reglas de forma automatizada
A través del método C4.5 se realiza el proceso de clasificación supervisada, con el objetivo de determinar, para un nuevo conjunto de datos (nuevo ejemplo), una valoración cualitativa de la precisión que obtendrían los clasificadores que se estudiaron. Aquí se utilizan para el entrenamiento los tres conjuntos de datos con los valores discretos de la precisión.
Los resultados del desempeño del C4.5 para estimar la precisión de los clasificadores a partir de las medidas propuestas, se muestran en la tabla 1. Estos son los resultados de aplicar una validación cruzada para diez muestras de prueba.
Tabla 1. Medidas de desempeño general al usar el método C4.5
Table 1. Measures of general performance obtained using C4.5 method
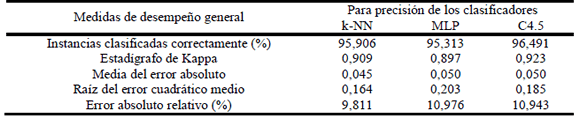
Clasificación supervisada usando una red neuronal Perceptron multicapaSe construye una red neuronal con cuatro neuronas en la capa de entrada, una capa oculta y cinco neuronas en la capa de salida, una para cada categoría. De esta manera se tiene una red neuronal que se entrena con tres conjuntos de datos (uno para cada clasificador del estudio con el atributo objetivo discretizado (clase)), capaz de decidir dado un nuevo conjunto de entrenamiento si es aplicable o no a cada clasificador, y en caso de ser aplicable, además da una valoración de la precisión que se obtendrá (baja, media, alta, muy alta). El desempeño de esta red neuronal para la prueba de validación cruzada (diez particiones) se muestra en la tabla 2.
Tabla 2. Medidas de desempeño general al usar el Perceptron Multicapa
Table 2. Measures of general performance obtained using the Multilayer Perceptron

Cuando se presenta un nuevo conjunto de entrenamiento, es decir un nuevo ejemplo, para predecir a priori el clasificador idóneo a aplicar, se procede según los pasos siguientes:
P1. Se particiona aleatoriamente el nuevo ejemplo en conjunto de entrenamiento (75%) y prueba (25%), esto se realiza diez veces y de esta forma se obtienen diez conjuntos de entrenamiento y diez de prueba.
P2. A cada uno de los diez conjuntos de entrenamiento, obtenidos en el paso P1 se le calculan las medidas: Calidad de la clasificación, Precisión generalizada de la clasificación, Calidad generalizada de la clasificación y Coeficiente de Aproximación General. Se obtiene para cada medida el valor promedio de los diez resultados.
P3. El nuevo ejemplo ahora está descrito por cuatro atributos asociados a las medidas, cuyos valores son los resultados de las medias obtenidas en el paso P2.
P4. Se determina para cada clasificador (k-NN, MLP, C4.5) la calidad de la precisión según las clases:
A->"No aplicable, precisión muy baja”
B-> "Aplicable, precisión baja”
C-> "Aplicable, precisión media”
D-> "Aplicable, precisión alta”
E->"Aplicable, precisión muy alta”
Esto puede realizarse a través del C4.5 o el Perceptron multicapa, ambos entrenados con los conjuntos de datos con los valores discretos de la precisión de los clasificadores.
P5. Se escoge como clasificador idóneo aquel que según el paso P4 le corresponda mejor valor de la clase, en el orden (E, D, C, B, A).
Estimación del valor de la precisión del clasificador más apropiado Luego de elegir el clasificador con el que se obtendrá más alta precisión para un conjunto de entrenamiento dado, se estima este valor a partir de los conjuntos de datos con los valores continuos de la precisión de los clasificadores, a través del método k-NN. Se calcula el valor de k óptimo y se obtiene un valor aproximado de la precisión del clasificador seleccionado. Los resultados obtenidos después de realizar una validación cruzada (diez muestras de prueba) se pueden observar en la tabla 3.
Tabla 3. Medidas de desempeño general al usar el método k-NN
Table 3. Measures of general performance obtained using k-NN method

5. CONCLUSIONES
Las medidas de inferencia basadas en la Teoría de los Conjuntos Aproximados: Calidad de la clasificación (medida clásica), así como Precisión generalizada de la clasificación, Calidad generalizada de la clasificación y el Coeficiente de aproximación general, las cuales se refieren al desempeño de todo el sistema de decisión, están altamente correlacionadas con el desempeño general de los clasificadores supervisados tales como el Perceptron multicapa,
C4.5 y k-NN. De igual forma, están altamente correlacionadas las medidas Calidad de la aproximación y Precisión de la aproximación, las cuales hacen una particularización por clases, con el desempeño por clases de los clasificadores antes mencionados.
La propuesta de construir conjuntos de datos de entrenamiento a partir de los resultados de las medidas de inferencia de la RST y los de la precisión de clasificadores supervisados (Perceptron multicapa, k-NN, C4.5), resultó exitosa para la generación de conocimiento, obteniéndose buenos desempeños en la clasificación supervisada a la hora de inferir a priori la precisión que se obtendrá con un nuevo conjunto de entrenamiento.
Todo lo anterior muestra que el empleo de la Teoría de los Conjuntos Aproximados permite la construcción de algoritmos para resolver de forma eficiente diversas tareas en el campo del aprendizaje automatizado.
REFERENCIAS
[1] RUIZ, R., de atributos para datos de gran dimensionalidad, in Departamento de Lenguajes y Sistemas Informáicos. 2006, Universidad de Sevilla: Sevilla. [ Links ]
[2] PAWLAK, Z., ROUGH SETS. International journal of Computer and Information Sciences, 1982. 11: p. 341-356. [ Links ]
[3] CHIN, K.S., J. Liang, and C. Dang. Rough Set Data Analysis Algorithms for Incomplete Information Systems. in Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. 9th International Conference, RSFDGRC2003. 2003. Chongqing, China. [ Links ]
[4] DJOUADI, A. The quality of training sets estimates of the Bhattacharyya Coefficient. Trans. On Pattern Recognition analysis and Machine learning 12(1): 92-97. 1990 [ Links ]
[5] FENG, C. AND D. MICHIE. STATLOG'S ML Algorithm. Machine Learning, Neural and Statistical Classification. D. Michie, D. J. Spiegelhalter and C. C. Taylor: 65-77. 1994 [ Links ]
[6] MICHIE, D., D. J. Spiegelhalter, et al. The Statlog Project. Machine Learning, Neural and Statistical Classification. D. Michie, D. J. Spiegelhalter and C. C. Taylor: 4. 1994 [ Links ]
[7] BEYNON, M. J. Degree of Dependency and Quality of Classification in the Extended Variable Precision Rough Sets Model. Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. 9th International Conference, RSFDGRC2003, Chongqing, China. 2003 [ Links ]
[8] CABALLERO, Y., R. BELLO, et al. Estudio de conjuntos de entrenamientos para redes tipo MLP usando medidas de la teoría de los conjuntos aproximados. I Simposio Iberoamericano de Inteligencia Artificial dentro de Informática'2004, La Habana. 2004 [ Links ]
[9] PARSONS, S., Current approaches to handling imperfect information in data and knowledges bases. IEEE Trans. On knowledge and data enginnering, 1996. 8(3). [ Links ]
[10] BAZAN, J., et al. A View on Rough Set Concept Approximations. in Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. 9th International Conference, RSFDGRC2003. 2003. Chongqing, China.
[11] KOMOROWSKI, J. and Z. Pawlak, Rough Sets: A tutorial. Rough Fuzzy Hybridization: A new trend in decision-making. Springer, 1999: p. 3-98. [ Links ]
[12] SLOWINSKI, R. and D. Vanderpooten, Similarity relation as a basis for rough approximations, in Advances in Machine Intelligence & Soft-Computing. 1997. p. 17-33. [ Links ]
[13] SKOWRON, A. and J. Stepaniuk. Intelligent systems based on rough set approach. in International Workshop Rough Sets. State of the Art and Perspectives. 1992. [ Links ]
[14] DEOGUN, J.S. Exploiting upper approximations in the rough set methodology. in First International Conference on Knowledge Discovery and Data Mining. 1995. Canada. [ Links ]
[15] PAL, S.K. and A. Skowron, Rough Fuzzy Hybridization: A New Trend in Decision-Making, ed. S. Springer-Verlag. 1999. [ Links ]
[16] SKOWRON, A. New directions in Rough Sets, Data Mining, and Granular Soft Computing. in 7th International Workshop (RSFDGRC'99), Yamaguchi, Japan. 1999. Lecture Notes in Artificial Intelligence 1711. [ Links ]
[17] GRABOWSKI, A., Basic Properties of Rough Sets and Rough Membership Function. Journal of Formalized Mathematics, 2003. 15. [ Links ]
[18] CABALLERO, Y., et al. New Measures for Evaluating Decision Systems using Rough Set Theory: The Application in Seasonal Weather Forecasting. in Third International ICSC Symposium on Information Technologies in Environmental Engineering (ITEE'07). 2007. Carl von Ossietzky Universität Oldenburg. Alemania: Springer Verlag. [ Links ]
[19] WITTEN, I. and E. Frank, Transformation: Engineering the input and output, in Data Mining. Practical Machine Learning Tools and Techniques, I. Witten and E. Frank, Editors. 2005. p. 296-304. [ Links ]














