Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.77 n.162 Medellín abr./jun. 2010
ALGUNAS CARTAS DE CONTROL BIVARIADAS PARA ATRIBUTOS
SOME BIVARIATE CONTROL CHARTS FOR ATRIBUTES
CAROLINA OSPINA HINCAPIE
Escuela de Estadística, Universidad Nacional de Colombia, Medellín, cospinah@unal.edu.co
SERGIO YAÑEZ CANAL
Escuela de Estadística, Universidad Nacional de Colombia, Medellín, syanez@unal.edu.co
CARLOS MARIO LOPERA GÓMEZ
Escuela de Estadística, Universidad Nacional de Colombia, Medellín, cmlopera@unal.edu.co
Recibido para revisar Junio 18 de 2010, aceptado Octubre 28 de 2009, versión final Octubre 30 de 2009
RESUMEN:Muchos procesos industriales son de naturaleza multivariada dado que la calidad de un producto depende de más de una variable. El control multivariado de procesos captura la relación en las variables asociadas al proceso, si se ignora esta correlación y se utilizan gráficos de control univariados para cada variable por separado se puede concluir erróneamente acerca del estado del proceso. En variables continuas correlacionadas se han realizado muchas investigaciones, sin embargo se encuentran pocos trabajos que traten sobre atributos correlacionados. En este trabajo se comparan tres cartas de control para variables aleatorias binomiales bivariadas, correlacionadas entre sí, las cuales miden atributos. Las cartas son: La carta 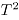 de Hotelling basada en la aproximación de la distribución binomial multivariada a la distribución normal multivariada. La carta MNP la cual es una extensión de las cartas
de Hotelling basada en la aproximación de la distribución binomial multivariada a la distribución normal multivariada. La carta MNP la cual es una extensión de las cartas 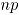 univariadas, y la carta
univariadas, y la carta 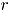 que es una metodología no paramétrica basada en el índice de profundidad de Mahalanobis. La comparación se hace vía simulación utilizando como medida de comparación, la longitud promedio de racha (ARL). Dentro del trabajo se presenta un ejemplo aplicado de las metodologías para construir cartas de control para variables binomiales bivariadas en una empresa de telecomunicaciones. De los resultados se aprecia, en términos generales, que la carta MNP es la mejor tanto en control como fuera de control.
que es una metodología no paramétrica basada en el índice de profundidad de Mahalanobis. La comparación se hace vía simulación utilizando como medida de comparación, la longitud promedio de racha (ARL). Dentro del trabajo se presenta un ejemplo aplicado de las metodologías para construir cartas de control para variables binomiales bivariadas en una empresa de telecomunicaciones. De los resultados se aprecia, en términos generales, que la carta MNP es la mejor tanto en control como fuera de control.
PALABRAS CLAVE: Cartas de Control Bivariadas, 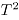 de Hotelling, Variables Binomiales Bivariadas, Carta de Control MNP, Carta de Control
de Hotelling, Variables Binomiales Bivariadas, Carta de Control MNP, Carta de Control 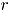 , Profundidad de Mahalanobis, ARL.
, Profundidad de Mahalanobis, ARL.
ABSTRACT:Many industrial processes are multivariate in nature since the quality of a product depends on more than one variable. The multivariate control of processes captures the relation between the variables associated with the process, if this correlation is ignored and univariate control charts are used for every variable separately is possible to conclude erroneously over the process status. In the continuous case, many researches have been done, however there are few works that aim to correlated attributes. In this work we compare three charts of control for correlated bivariate binomial random variables, which are associated with attributes. The charts are: Hotelling's 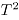 chart based on the approximation of the distribution binomial multivariate to the normal multivariate distribution. MNP chart which is an extension of univariate
chart based on the approximation of the distribution binomial multivariate to the normal multivariate distribution. MNP chart which is an extension of univariate 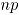 chart, and
chart, and 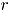 chart that is a non-parametric methodology based on the Mahalanobis's depth. The comparison is made through of simulation study using as a comparison measure the average run length (ARL). In this work we present an example of the used methodologies to construct control charts for bivariate binomial variables in a telecommunications company. The results shown in general terms that the MNP chart is the best in both control and out of control.
chart that is a non-parametric methodology based on the Mahalanobis's depth. The comparison is made through of simulation study using as a comparison measure the average run length (ARL). In this work we present an example of the used methodologies to construct control charts for bivariate binomial variables in a telecommunications company. The results shown in general terms that the MNP chart is the best in both control and out of control.
KEYWORDS: Control Bivariate Charts, Hotelling's 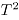 , Bivariate Binomial Variables, MNP Control Chart,
, Bivariate Binomial Variables, MNP Control Chart, 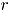 Control Chart, Mahalanobis's Depth, ARL
Control Chart, Mahalanobis's Depth, ARL
1. INTRODUCCIÓN
En el mundo de las organizaciones no todos los procesos que se desean medir se pueden describir mediante variables continuas [1], los atributos asociados a los procesos de servicio al cliente, como son: la satisfacción con la venta, la satisfacción con la facturación, entre otros; son variables discretas que deben ser controladas para la administración efectiva de los clientes. Por lo tanto se requiere de metodologías que permitan establecer estándares de cumplimiento también para este tipo de problemas [2].Existen diversas situaciones en las cuales más de una variable se debe considerar de manera simultánea, por ejemplo la satisfacción con el servicio de internet de banda ancha y la disponibilidad de la red de acceso. El control multivariado de procesos es ideal para capturar la relación que existe entre las variables que determinan la calidad de un producto o servicio, por lo tanto si se ignora esta correlación y se utilizan cartas de control univariadas para cada variable por separado, se puede perder información importante [3].Entre los métodos más usados para construir cartas de control multivariadas se encuentra la carta de control 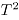 de Hotelling, sin embargo este método se restringe, usualmente, al caso de distribuciones normales [4]. En variables continuas correlacionadas se han realizado muchas investigaciones, sin embargo se encuentran pocos trabajos que traten sobre atributos correlacionados [2].En este trabajo se estudian variables aleatorias binomiales bivariadas correlacionadas, que miden atributos y se indaga sobre cuál metodología es adecuada para establecer un control efectivo sobre procesos que sean medidos con dichas variables. Se comparan tres métodos para construir cartas de control para variables binomiales bivariadas correlacionadas.
de Hotelling, sin embargo este método se restringe, usualmente, al caso de distribuciones normales [4]. En variables continuas correlacionadas se han realizado muchas investigaciones, sin embargo se encuentran pocos trabajos que traten sobre atributos correlacionados [2].En este trabajo se estudian variables aleatorias binomiales bivariadas correlacionadas, que miden atributos y se indaga sobre cuál metodología es adecuada para establecer un control efectivo sobre procesos que sean medidos con dichas variables. Se comparan tres métodos para construir cartas de control para variables binomiales bivariadas correlacionadas.
El primer método es la carta 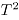 de Hotelling o carta AN, basada en la aproximación de la distribución binomial multivariada a la distribución normal multivariada [5]. El segundo método es la carta MNP que consiste en la extensión multivariada de las cartas
de Hotelling o carta AN, basada en la aproximación de la distribución binomial multivariada a la distribución normal multivariada [5]. El segundo método es la carta MNP que consiste en la extensión multivariada de las cartas 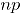
univariadas [2], y la carta 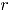 , la cual emplea un método no paramétrico basado en el índice de profundidad de Mahalanobis [4]. En la sección 2 se revisan los conceptos básicos de la construcción de las cartas de control bivariadas.
, la cual emplea un método no paramétrico basado en el índice de profundidad de Mahalanobis [4]. En la sección 2 se revisan los conceptos básicos de la construcción de las cartas de control bivariadas.
La sección 3 presenta la metodología de simulación, se detallan los algoritmos empleados y se delimitan los escenarios a ser considerados. Los resultados de la comparación de las tres metodologías, mediante el comportamiento del ARL en control y fuera de control se presentan en la sección 4. La sección 5 presenta un ejemplo aplicado a la industria de telecomunicaciones, el cual ilustra el uso de las tres metodologías. Por último, la sección 6 muestra las conclusiones del trabajo.
2. CONCEPTOS BÁSICOS EN CARTAS DE CONTROL BIVARIADAS
2.1 Construcción de cartas de control
La construcción de cartas de control se puede dividir en las siguientes fases [6]:
- Fase I: se estiman los parámetros del proceso (estándares de calidad) y se hallan los límites de control.
- Fase II: para cada observación se calcula el estadístico asociado a la carta y se compara con los límites de control definidos en la fase I, con el fin de determinar si el proceso está en control o fuera de control.
2.2 Distribución Binomial Bivariada
Si se consideran dos variables aleatorias 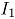 e
e 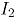 , las cuales pueden tomar dos posibles valores: 1, si el ensayo resulta un éxito en la variable
, las cuales pueden tomar dos posibles valores: 1, si el ensayo resulta un éxito en la variable 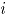 ó 0, en otro caso,
ó 0, en otro caso, 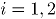 ; La distribución conjunta de la variable
; La distribución conjunta de la variable 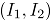 es Bernoulli bivariada, con probabilidad conjunta
es Bernoulli bivariada, con probabilidad conjunta 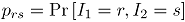 , para
, para 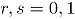 ; cuya función generadora de probabilidad (fgp) conjunta de
; cuya función generadora de probabilidad (fgp) conjunta de 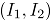 es [7]:
es [7]:
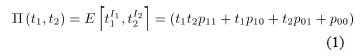
Usando la ecuación anterior es posible determinar los momentos de la distribución Bernoulli bivariada, en particular: 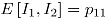 y
y 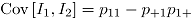 , así el coeficiente de correlación es:
, así el coeficiente de correlación es:
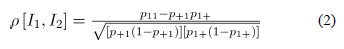
Una propiedad interesante proveniente de fgp conjunta (1) es que las fgp's marginales son:
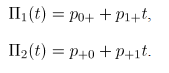
Donde, cada distribución marginal es una distribución Bernoulli [7].
Considere ahora una secuencia de 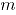 ensayos Bernoulli bivariados. Defina
ensayos Bernoulli bivariados. Defina 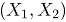 como:
como:
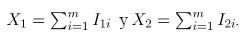
La distribución conjunta de 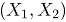 es binomial bivariada [8]. Luego, partiendo de (1), la fgp conjunta de
es binomial bivariada [8]. Luego, partiendo de (1), la fgp conjunta de 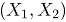 , es:
, es:
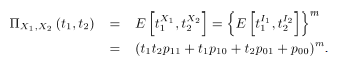
Las fgp's de las marginales para 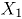 y
y 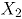 son:
son:
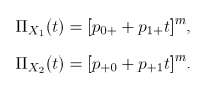
Cada una de cuales corresponde a una distribución binomial con el mismo número de ensayos 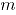 , pero con probabilidades de éxito
, pero con probabilidades de éxito 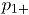 y
y 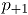 , para
, para 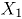 y
y 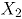 , respectivamente. En adelante
, respectivamente. En adelante 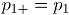 y
y 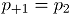 .
.
La correlación entre 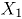 y
y 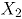 es la misma que en el caso Bernoulli bivariado, que se mostró en (2).
es la misma que en el caso Bernoulli bivariado, que se mostró en (2).
Sea 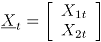 un vector aleatorio binomial bivariado con parámetros
un vector aleatorio binomial bivariado con parámetros  y
y  , tomado en el tiempo t. Si se tiene una muestra de vectores de las características de
, tomado en el tiempo t. Si se tiene una muestra de vectores de las características de 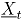 , recolectada a través de
, recolectada a través de 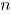 puntos diferentes en el tiempo, entonces una matriz de datos binomiales bivariados tiene la siguiente representación:
puntos diferentes en el tiempo, entonces una matriz de datos binomiales bivariados tiene la siguiente representación:
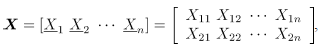
donde, 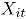 es el conteo de unidades no conformes en el atributo
es el conteo de unidades no conformes en el atributo 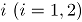 , tomado en el tiempo
, tomado en el tiempo 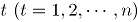 . En el contexto del artículo, la matriz
. En el contexto del artículo, la matriz  constituye el conjunto de datos históricos en control.
constituye el conjunto de datos históricos en control.
En adelante se asumirá que 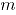 hace referencia al tamaño de la submuestra y
hace referencia al tamaño de la submuestra y 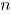 indica el número de observaciones tomadas en el tiempo o tamaño de muestra. Para más detalles sobre la distribución binomial bivariada [9].
indica el número de observaciones tomadas en el tiempo o tamaño de muestra. Para más detalles sobre la distribución binomial bivariada [9].
2.3 Carta de control AN
Basados en un conjunto de datos histórico 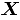 , y asumiendo independencia de las observaciones sucesivas en el tiempo, el vector de medias
, y asumiendo independencia de las observaciones sucesivas en el tiempo, el vector de medias  y la matriz de covarianzas
y la matriz de covarianzas 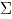 , asociados a
, asociados a 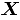 , se pueden estimar respectivamente mediante:
, se pueden estimar respectivamente mediante:
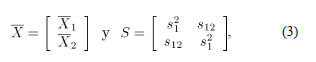
donde, para 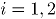 se tiene que:
se tiene que:
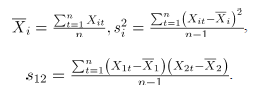
La media muestral 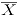 será tomada como un estándar deseable para que el proceso esté en control.
será tomada como un estándar deseable para que el proceso esté en control.
El estadístico para la carta de control AN se define como:
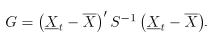
Para valores suficientemente grandes de 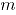 y
y 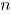 ,
, 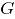 tiene aproximadamente una distribución
tiene aproximadamente una distribución 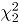 , de manera que el límite superior de control
, de manera que el límite superior de control 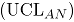 de esta carta de control es el valor
de esta carta de control es el valor 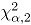 , donde
, donde 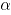 es el nivel de significancia especificado, mientras que el límite inferior de control
es el nivel de significancia especificado, mientras que el límite inferior de control 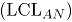 es cero.
es cero.
El estimador 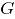 es equivalente al estadístico
es equivalente al estadístico 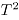 de Hotteling tradicional en cartas de control multivariadas. En adelante el estadístico
de Hotteling tradicional en cartas de control multivariadas. En adelante el estadístico 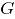 se denotará como
se denotará como 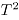 .
.
2.4 Carta de control MNP
En la referencia [2] se presenta una metodología para desarrollar control estadístico de calidad multivariado para variables tipo atributos, donde se define el estadístico como la suma ponderada de los conteos de unidades no conformes de cada característica de calidad en una muestra.
En el caso bivariado, si 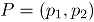 es el vector de fracciones de no conformidad, y
es el vector de fracciones de no conformidad, y 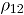 la correlación entre los dos atributos bajo estudio, entonces, para un periodo de tiempo fijo
la correlación entre los dos atributos bajo estudio, entonces, para un periodo de tiempo fijo 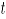 , el estadístico para la carta MNP [2] es:
, el estadístico para la carta MNP [2] es:
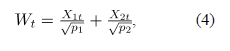
con las siguientes propiedades:
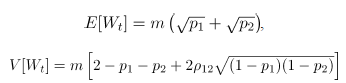
Cuando el vector de fracciones de no conformidad del proceso 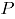 y la correlación entre atributos
y la correlación entre atributos 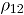 no son conocidos, deben ser estimados mediante los datos históricos en control, contenidos en la matriz
no son conocidos, deben ser estimados mediante los datos históricos en control, contenidos en la matriz 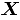 . Luego, el vector de fracciones de no conformidad se estima como [2]:
. Luego, el vector de fracciones de no conformidad se estima como [2]:
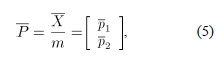
Siendo 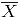 estimado como en (3)
estimado como en (3)
La correlación entre los atributos 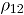 se estima también a partir de la matriz
se estima también a partir de la matriz 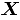 , como:
, como:
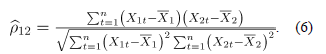
Conociendo las estimaciones del vector 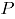 y de la correlación
y de la correlación 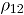 , la línea central
, la línea central 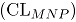 y los límites de control (
y los límites de control ( 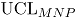 : límite superior y
: límite superior y 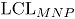 : límite inferior) de las cartas MNP son:
: límite inferior) de las cartas MNP son:
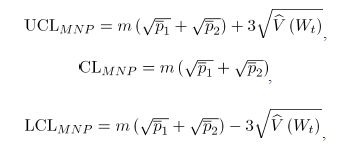
donde 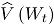 se obtiene reemplazando las estimaciones muestrales de
se obtiene reemplazando las estimaciones muestrales de 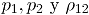 . Si el estadístico
. Si el estadístico 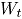 cae dentro de los límites de control, se puede concluir que el proceso bivariado está en control [2].
cae dentro de los límites de control, se puede concluir que el proceso bivariado está en control [2].
2.5 Carta de control 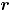
La carta de control 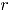 se fundamenta en la noción de profundidad de los datos, la cual se basa en el hecho de que cualquier densidad de probabilidad distingue entre puntos centrales y periféricos. Las profundidades más grandes corresponden al centro de la distribución, mientras que las más pequeñas corresponden a regiones externas [3].
se fundamenta en la noción de profundidad de los datos, la cual se basa en el hecho de que cualquier densidad de probabilidad distingue entre puntos centrales y periféricos. Las profundidades más grandes corresponden al centro de la distribución, mientras que las más pequeñas corresponden a regiones externas [3].
Una medida de profundidad muy utilizada es la profundidad de Mahalanobis, la cual se define para un vector aleatorio 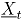 , que proviene de una distribución de referencia
, que proviene de una distribución de referencia 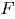 en
en 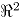 , como [4]:
, como [4]:
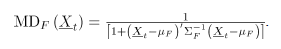
Donde 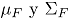 son respectivamente el vector de medias y la matriz de covarianzas de la distribución de referencia
son respectivamente el vector de medias y la matriz de covarianzas de la distribución de referencia 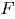 . Si los parámetros de la distribución de referencia no son conocidos, entonces la versión muestral de
. Si los parámetros de la distribución de referencia no son conocidos, entonces la versión muestral de 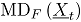 es:
es:
. 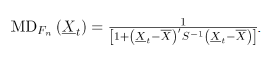
Donde 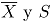 son respectivamente el vector de medias y la matriz de covarianzas muestrales de los datos históricos en control
son respectivamente el vector de medias y la matriz de covarianzas muestrales de los datos históricos en control 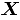 , asociados a la distribución empírica
, asociados a la distribución empírica 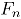 [10], y que son estimados mediante la expresión (3).
[10], y que son estimados mediante la expresión (3).
Sean 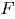 y
y 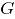 las funciones de distribución de dos poblaciones independientes bidimensionales. Suponga que la matriz
las funciones de distribución de dos poblaciones independientes bidimensionales. Suponga que la matriz 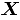 es una muestra tomada de la distribución de referencia
es una muestra tomada de la distribución de referencia 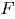 , la cual está en control. Sea
, la cual está en control. Sea 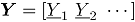 una muestra aleatoria tomada desde una población que tiene distribución
una muestra aleatoria tomada desde una población que tiene distribución 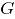 (una nueva medida tomada del proceso). Para determinar si la muestra
(una nueva medida tomada del proceso). Para determinar si la muestra 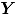 está en control, se deben comparar las distribuciones
está en control, se deben comparar las distribuciones 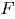 y
y 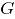 , mediante la siguiente prueba de hipótesis:
, mediante la siguiente prueba de hipótesis:

Para probar esta hipótesis, se usa el estadístico:
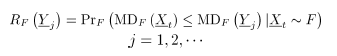
que caracteriza la distancia entre  y
y  con respecto a la profundidad de Mahalanobis. Bajo la hipótesis
con respecto a la profundidad de Mahalanobis. Bajo la hipótesis 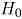 , si
, si 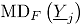 es continua, la distribución de
es continua, la distribución de 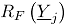 definida anteriormente es uniforme en
definida anteriormente es uniforme en 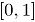 [11]. Cuando la distribución
[11]. Cuando la distribución 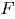 es desconocida la versión muestral del estadístico
es desconocida la versión muestral del estadístico 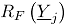 es:
es:
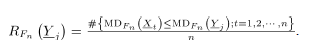
Los límites de la carta 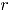 se basan en que bajo
se basan en que bajo 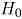 ,
, 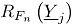 es aproximadamente una distribución uniforme en
es aproximadamente una distribución uniforme en 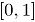 , cuyo valor esperado es 0.5
, cuyo valor esperado es 0.5 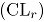 . Como el valor de
. Como el valor de 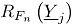 indica la probabilidad de que
indica la probabilidad de que 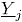 sea un punto dentro del conjunto de datos histórico en control
sea un punto dentro del conjunto de datos histórico en control 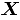 , entonces el límite de control inferior
, entonces el límite de control inferior 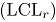 es
es 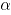 . Donde,
. Donde, 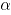 es la proporción de falsa alarma [3]. Por diseño el límite de control superior
es la proporción de falsa alarma [3]. Por diseño el límite de control superior 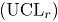 se asume con valor de uno.
se asume con valor de uno.
En una carta de control 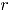 cuando los valores de
cuando los valores de 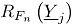 están en la región
están en la región 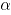 (entre 0 y
(entre 0 y 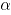 ) el proceso está fuera de control estadístico [10].
) el proceso está fuera de control estadístico [10].
3. ESTUDIO DE SIMULACIÓN
Para analizar las tres metodologías para construir cartas de control para variables binomiales bivariadas (Cartas AN, MNP y 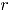 ), se controlan factores que afectan su desempeño: a) Nivel de correlación entre los dos atributos
), se controlan factores que afectan su desempeño: a) Nivel de correlación entre los dos atributos 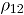 , b) Las proporciones de no conformidad
, b) Las proporciones de no conformidad 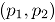 y c) El tamaño de la submuestra
y c) El tamaño de la submuestra 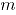 . Esto con el fin de analizar la rapidez de cada uno de los métodos en la detección de un punto fuera de control.
. Esto con el fin de analizar la rapidez de cada uno de los métodos en la detección de un punto fuera de control.
3.1 Factores de simulación y sus niveles
Se consideraron tres niveles de correlación 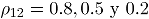 , que corresponden a niveles de correlación fuerte, moderado y débil, respectivamente. Se seleccionaron tres niveles para las proporciones de no conformidad, así:
, que corresponden a niveles de correlación fuerte, moderado y débil, respectivamente. Se seleccionaron tres niveles para las proporciones de no conformidad, así: 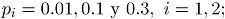 que representan a proporciones de no conformidad baja, media y alta [1]. Los tamaños de submuestra
que representan a proporciones de no conformidad baja, media y alta [1]. Los tamaños de submuestra 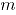 fueron calculados a partir de las siguientes situaciones:
fueron calculados a partir de las siguientes situaciones:
- Caso 1. Tamaño de submuestra que favorece la aproximación de la distribución binomial bivaridada a la distribución normal bivariada.
- Caso 2. Tamaño recomendado por la referencia [2] para la construcción de cartas MNP.
- Caso 3. Tamaño basado en la condición de que al menos se encuentre una observación no conforme en la muestra [1].
3.2 Generación de los datos
Los datos para todo el estudio de simulación son construidos a partir del algoritmo de Ong [12]. Este algoritmo genera variables binomiales bivariadas a partir de las proporciones de no conformidad de las marginales 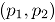 y la correlación entre las variables
y la correlación entre las variables 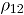 .
.
La siguiente tabla resume los tamaños de submuestra calculados en los tres casos definidos en la sección 3.1, para las combinaciones de los factores 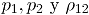 .
.
Tabla 1. Tamaños de submuestra para los escenarios de simulación.
Table 1. Subsample sizes for the simulation scenarios
En algunas combinaciones de  (marcadas en la Tabla 1, con sombreado) donde los atributos tienen valores para las proporciones de no conformidad considerablemente diferentes, el algoritmo de Ong no converge. Adicionalmen-te, algunos tamaños de submuestra correspon-dientes a los Casos 2 y 3 resultaron iguales. Lo anterior lleva a considerar 23 posibles combina-ciones diferentes de
(marcadas en la Tabla 1, con sombreado) donde los atributos tienen valores para las proporciones de no conformidad considerablemente diferentes, el algoritmo de Ong no converge. Adicionalmen-te, algunos tamaños de submuestra correspon-dientes a los Casos 2 y 3 resultaron iguales. Lo anterior lleva a considerar 23 posibles combina-ciones diferentes de  con su tamaño de submuestra calculado.
con su tamaño de submuestra calculado.
En adelante se empleará la siguiente notación para los subíndices, 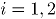 ; se refiere a los atributos,
; se refiere a los atributos, 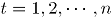 ; indica el número de observaciones en el tiempo, y
; indica el número de observaciones en el tiempo, y 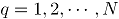 ; es el número de simulaciones. En todos los escenarios de simulación se emplea la misma combinación de subíndices
; es el número de simulaciones. En todos los escenarios de simulación se emplea la misma combinación de subíndices 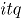 .
.
3.3 Metodología de simulación
Para cada escenario de simulación se generaron 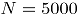 simulaciones que representan los datos históricos que denotaremos
simulaciones que representan los datos históricos que denotaremos 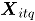 con
con 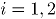 ;
; 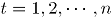 ; y
; y 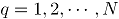 . Sobre los datos históricos se estiman (en Fase I) los parámetros del proceso (estándares de calidad) y los límites de control para cada una de las cartas descritas en la sección 2.
. Sobre los datos históricos se estiman (en Fase I) los parámetros del proceso (estándares de calidad) y los límites de control para cada una de las cartas descritas en la sección 2.
Con el objetivo de examinar la rapidez con que cada uno de los métodos detecta, en Fase II, desviaciones de los datos con respecto a la media. Para cada escenario de simulación se generaron 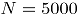 simulaciones en control denotadas
simulaciones en control denotadas 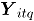 , las cuales se contaminan mediante la desviación estándar de cada atributo de la siguiente manera:
, las cuales se contaminan mediante la desviación estándar de cada atributo de la siguiente manera:
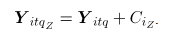
Donde, para la simulación 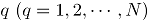 ,
, 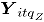 se refiere a la
se refiere a la 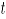 -ésima observación contaminada del
-ésima observación contaminada del 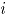 -ésimo atributo,
-ésimo atributo, 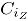 es la contaminación
es la contaminación 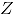 , para el atributo
, para el atributo 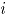 , donde
, donde 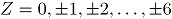 son los niveles de contaminación tanto en dirección positiva (signo "+") como en dirección negativa (signo "-") a partir de la media del proceso en control. Las contaminaciones se resumen en la siguiente tabla.
son los niveles de contaminación tanto en dirección positiva (signo "+") como en dirección negativa (signo "-") a partir de la media del proceso en control. Las contaminaciones se resumen en la siguiente tabla.
Tabla 2. Niveles de contaminación
Table 2. Contamination Level
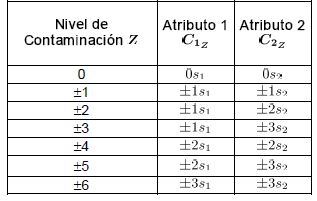
De la Tabla 2 se observa que 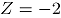 , representa contaminaciones para los atributos 1 y 2, en la dirección negativa de magnitud
, representa contaminaciones para los atributos 1 y 2, en la dirección negativa de magnitud 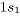 y
y 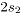
respectivamente. 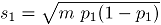 y
y 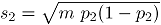 son las respectivas desviaciones estándar de cada atributo. Las contaminaciones se realizan en la misma dirección, pues la correlación se trabaja en valores positivos. Por último,
son las respectivas desviaciones estándar de cada atributo. Las contaminaciones se realizan en la misma dirección, pues la correlación se trabaja en valores positivos. Por último,  , hace referencia a los datos en control.
, hace referencia a los datos en control.
Para la construcción de las cartas de control primero se estiman los parámetros, luego se calculan los límites de control y por último se establece la medida de comparación.
El criterio de comparación utilizado fue la longitud promedio de racha (ARL) tanto en control como fuera de control, es decir, el número promedio de mediciones en la carta hasta encontrar una señal fuera de control. Lo ideal es encontrar una carta con un ARL en control grande y un ARL fuera de control pequeño.
Una forma general de calcular el ARL se obtiene al invertir la proporción de observaciones fuera de control, así:
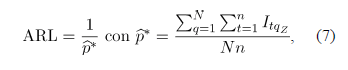
donde, 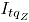 se define apropiadamente para cada carta de control.
se define apropiadamente para cada carta de control.
Estimadores de los parámetros: Para cada simulación se estiman los parámetros mediante la expresión (3). Luego se promedian los valores obtenidos en las 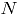 simulaciones, así:
simulaciones, así:
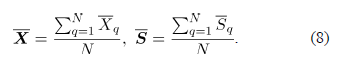
Límite de control: El límite de control depende de los factores 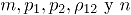 ; por lo tanto es necesario calcularlo de manera empírica, se utiliza en este trabajo la metodología propuesta en [6], que se describe a continuación:
; por lo tanto es necesario calcularlo de manera empírica, se utiliza en este trabajo la metodología propuesta en [6], que se describe a continuación:
- Para cada uno de los datos históricos generados
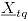 , se calcula el estadístico
, se calcula el estadístico 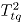 .
. - En cada simulación
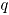 se calcula el máximo
se calcula el máximo 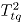 .
. - El
 se obtienen como el percentil 95 de la distribución empírica del estadístico
se obtienen como el percentil 95 de la distribución empírica del estadístico 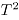 , generada en el punto anterior.
, generada en el punto anterior.
Medida de comparación: Se utiliza el ARL, el cual se calcula como en la expresión (7), teniendo en cuenta que 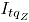 se define como:
se define como:
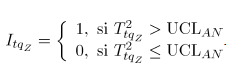
Estimadores de los parámetros: en cada simulación se estiman las proporciones de no conformidad y la correlación entre atributos como en las expresiones (5) y (6). Luego se promedian estos valores para las
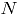 simulaciones, así:
simulaciones, así: 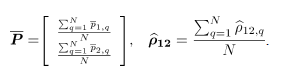
Límites de control: Empleando el mismo concepto de la carta AN para cada simulación 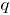 se calculan los límites de control
se calculan los límites de control 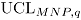 y
y 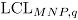 , obteniendo así una distribución empírica para los límites de control de la carta MNP. Luego, se estiman el
, obteniendo así una distribución empírica para los límites de control de la carta MNP. Luego, se estiman el 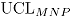 y el
y el 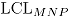 como los percentiles 97.5 en cada caso.
como los percentiles 97.5 en cada caso.
Medida de comparación: En este caso, el cálculo del ARL utiliza en la expresión (7) la siguiente definición para 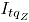 :
:
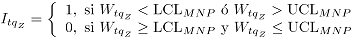 ,
,
donde, 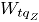 es el valor del estadístico MNP resultante de aplicar la ecuación (4) en la simulación
es el valor del estadístico MNP resultante de aplicar la ecuación (4) en la simulación 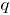 , bajo un nivel de contaminación
, bajo un nivel de contaminación 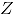 .
.
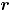
Estimadores de los parámetros: Igual que para la carta AN en cada simulación se estiman los parámetros mediante la expresión (3) y se promedian los valores obtenidos en las
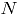 simulaciones, llegando a la expresión (8).
simulaciones, llegando a la expresión (8). Límite de control: En cada simulación 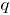 se toma la mínima profundidad
se toma la mínima profundidad 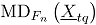 , obteniendo una distribución empírica de las mínimas profundidades de Mahalanobis. Luego el
, obteniendo una distribución empírica de las mínimas profundidades de Mahalanobis. Luego el 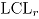 se calcula como el percentil 5 de esta distribución empírica.
se calcula como el percentil 5 de esta distribución empírica.
Medida de comparación: Para la carta 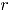 el cálculo del ARL utiliza en la expresión (7) la siguiente definición para
el cálculo del ARL utiliza en la expresión (7) la siguiente definición para 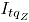 :
:
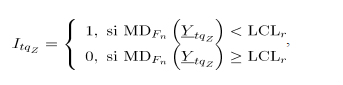
donde, 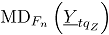 es la profundidad de Mahalanobis para la
es la profundidad de Mahalanobis para la 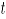 -ésima observación contaminada a nivel
-ésima observación contaminada a nivel 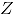 .
.
4. RESULTADOS
En la Tabla 3, que consta de tres filas y tres columnas, se resumen de manera gráfica los resultados del estudio de simulación cuando las proporciones de no conformidad son iguales. Las filas de la tabla hacen referencia a los casos de simulación y las columnas corresponden a las proporciones de no conformidad estudiadas. Cada celda en la tabla consta de tres figuras (cada una de ellas asociada a un nivel de correlación distinto) donde se muestran los ARL's obtenidos en función del nivel de contaminación 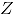 . Por ejemplo, la celda ubicada en la fila 1, columna 3 presenta los resultados para proporciones de no conformidad iguales a 0.3, con tamaños de submuestra calculados para el caso 1 y en las tres correlaciones.De la Tabla 3 se puede concluir que la carta MNP presenta un comportamiento similar bajo cualquiera de las situaciones de simulación consideradas. En tal comportamiento se destaca que la carta MNP tiene valores de ARL menores o muy cercanos a los de las otras cartas excepto cuando se tiene un nivel de contaminación
. Por ejemplo, la celda ubicada en la fila 1, columna 3 presenta los resultados para proporciones de no conformidad iguales a 0.3, con tamaños de submuestra calculados para el caso 1 y en las tres correlaciones.De la Tabla 3 se puede concluir que la carta MNP presenta un comportamiento similar bajo cualquiera de las situaciones de simulación consideradas. En tal comportamiento se destaca que la carta MNP tiene valores de ARL menores o muy cercanos a los de las otras cartas excepto cuando se tiene un nivel de contaminación 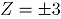 y bajo una correlación alta de
y bajo una correlación alta de 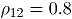 donde las cartas AN y
donde las cartas AN y  tienen un ARL apreciablemente menor. Cuando la contaminación se da en la dirección negativa, los ARL's obtenidos en las cartas AN y
tienen un ARL apreciablemente menor. Cuando la contaminación se da en la dirección negativa, los ARL's obtenidos en las cartas AN y  presentan en la mayoría de los casos valores significativamente superiores a los de la carta MNP, lo cual se agrava para los tamaños de submuestra correspondientes a los casos 2 y 3. En este sentido el nivel de correlación actúa como un factor atenuante ya que cuando éste disminuye los ARL's de las cartas se acercan.
presentan en la mayoría de los casos valores significativamente superiores a los de la carta MNP, lo cual se agrava para los tamaños de submuestra correspondientes a los casos 2 y 3. En este sentido el nivel de correlación actúa como un factor atenuante ya que cuando éste disminuye los ARL's de las cartas se acercan.
Tabla 3. Matriz de gráficos para los resultados de simulación cuando las proporciones de no conformidad son iguales.
Table 3. Matrix of graphs for the simulation results when of the nonconforming proportions are equal.
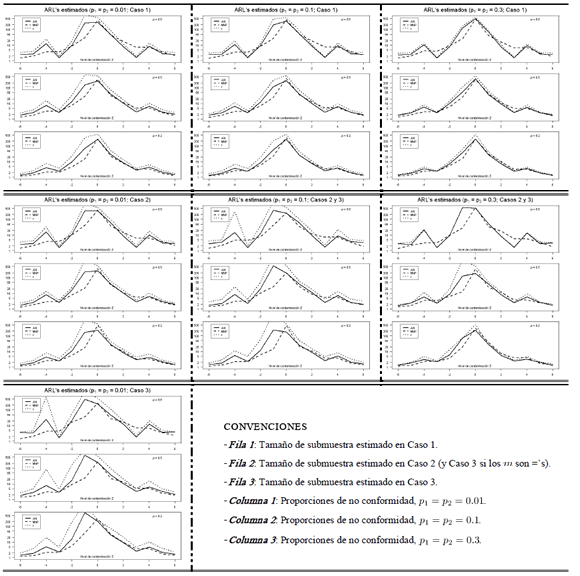
Ahora, si la contaminación se da en la dirección positiva las cartas de control estudiadas en general presentan ARL's muy similares, lo cual se acentúa a medida que disminuye el nivel de correlación. En términos generales se puede concluir que al aumentar las proporciones de no conformidad en los atributos se logran atenuar las diferencias entre los ARL's obtenidos en las tres cartas estudiadas.A continuación se muestran los resultados obtenidos en el caso de proporciones de no conformidad diferentes en los atributos.
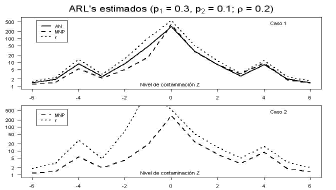
Figura 1. Resultados de simulación para proporciones de no conformidad diferentes.
Figure 1. Simulation Results for diferent nonconforming proportions.
Cuando las proporciones de no conformidad en los atributos son diferentes en el Caso 1 no se observan conclusiones diferentes a las reportadas en el análisis de la matriz de gráficos (Tabla 3), en el Caso 2 cabe notar que la carta AN, no arrojó ningún dato fuera de control, en este caso el tamaño muestral es pequeño 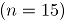 , mientras que las cartas MNP y
, mientras que las cartas MNP y  si detectaron puntos fuera de control, sin embargo el mejor comportamiento en esta situación es para la carta MNP.
si detectaron puntos fuera de control, sin embargo el mejor comportamiento en esta situación es para la carta MNP.
5. APLICACIÓN CON DATOS REALES
En el área de servicio al cliente de una importante Empresa de Servicios de Telecomunicaciones se quiere establecer un sistema de control que les permita evaluar la percepción del cliente con respecto a las premisas estratégicas básicas de servicio: El cumplimiento del tiempo acordado en suministrar el servicio solicitado por el cliente y el funcionamiento adecuado de los servicios prestados, apuntado a un factor diferenciador "La Oportunidad", este atributo es altamente valorado por el cliente de la compañía. Por lo tanto se puede representar lo anterior mediante dos variables Bernoulli, así:

Observe que 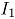 representa la no conformidad de los clientes con el cumplimiento en el tiempo acordado para suministrar el servicio, mientras que
representa la no conformidad de los clientes con el cumplimiento en el tiempo acordado para suministrar el servicio, mientras que 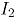 es la no conformidad del cliente con el funcionamiento adecuado de los servicios prestados en la actividad solicitada.
es la no conformidad del cliente con el funcionamiento adecuado de los servicios prestados en la actividad solicitada.
La empresa desea determinar cuándo se presenta un deterioro en la calidad del servicio a través de de los dos atributos definidos. Para lograr definir la calidad del servicio prestado se comenzó a medir diariamente los dos atributos mediante una encuesta telefónica, aplicada a clientes a los que se les instaló un servicio de telecomunicaciones. La encuesta se genera automáticamente cuando se cierra el servicio prestado. La medición se empezó a realizar a partir del mes de octubre de 2008, durante este mes se observaron los resultados y los datos históricos fueron extraídos en el mes de noviembre de 2008. Se tomaron aleatoriamente 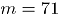 clientes, agrupados por fecha de solicitud de servicio y se les preguntó acerca de su percepción del cumplimiento y el adecuado funcionamiento del servicio solicitado. A continuación se muestran las gráficas del número de clientes inconformes en estos dos atributos durante un seguimiento de
clientes, agrupados por fecha de solicitud de servicio y se les preguntó acerca de su percepción del cumplimiento y el adecuado funcionamiento del servicio solicitado. A continuación se muestran las gráficas del número de clientes inconformes en estos dos atributos durante un seguimiento de 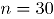 días (Fase I).
días (Fase I).
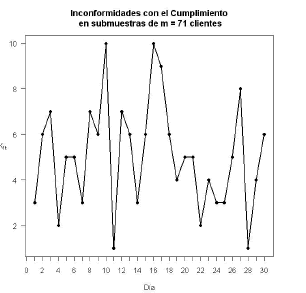
Figura 2. Inconformidades en el Cumplimiento (Fase 1).
Figure 2. Unconformities in the compliance (Phase I).
De la gráfica anterior se puede observar que en promedio a 5 clientes por día en la muestra no se les cumplió con el tiempo acordado en suministrar el servicio, no hay ningún tipo de tendencia en el gráfico de control del atributo, lo que indica que el atributo cumplimiento en el periodo de evaluación se puede considerar un estándar de servicio.
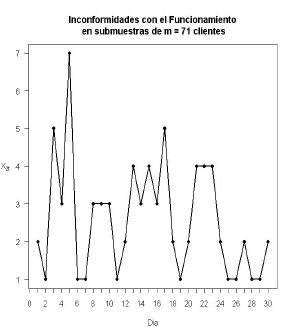
Figura 3. Inconformidades en el Funcionamiento (Fase 1).
Figure 3. Unconformities in the operation (Phase I)
Con respecto al atributo funcionamiento en los primeros seis días de evaluación de los datos históricos se presentaron comportamientos atípicos, debido a problemas en los sistemas de información que fueron corregidos, sin embargo se determinó que el atributo se podría considerar controlado corrigiendo las causas de los puntos fuera de control.
Partiendo del conjunto de datos históricos se determinan los parámetros del proceso en control como se describió en la sección 2, obteniendo los siguientes resultados.
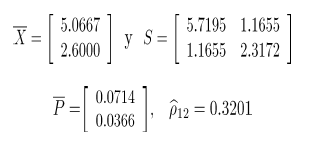
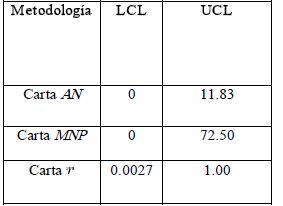
Ahora, con base en las estimaciones anteriores se calculan los límites de control, para cada una de las metodologías estudiadas en la sección 2, cuyos resultados se resumen en la Tabla 4.
Tabla 4. Límites de control para cartas bivariadas
Table 4. Control's limits for bivariate charts
A continuación se muestran las cartas de control resultantes de aplicar las tres metodologías a los datos en Fase I y a un monitoreo posterior de clientes por 25 días en dic/2008 (Fase II).
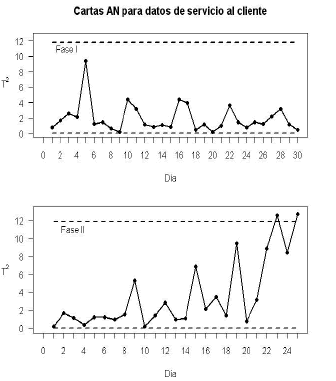
Figura 4. Carta AN para datos reales.
Figure 4. AN chart for real data.
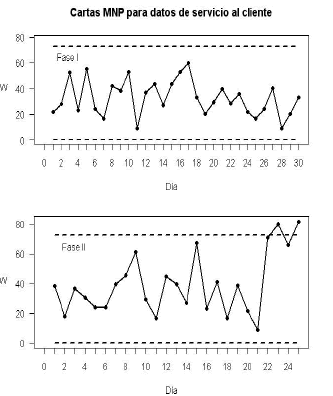
Figura 5. Carta MNP para datos reales.
Figure 5. MNP chart for real data.
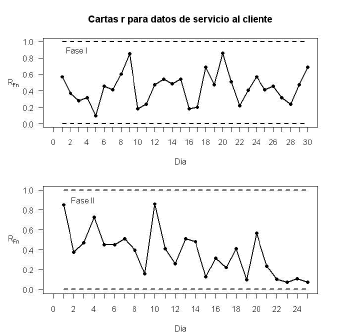
Figura 6. Carta  para datos reales.
para datos reales.
Figure 6.  chart for real data.
chart for real data.
A partir de los resultados anteriores se determina que el proceso está fuera de control mediante las cartas de control AN y MNP, las cuales ubican dos puntos fuera de control, aunque se puede remarcar que en la carta MNP los puntos fuera de control están más alejados del límite de control superior. Por otra parte, aún cuando la carta 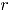 no detecta ningún punto fuera de control, se observa una tendencia decreciente en el estadístico
no detecta ningún punto fuera de control, se observa una tendencia decreciente en el estadístico 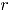 . Haciendo una revisión detallada del proceso se logró establecer que las causas para que éste se encontrara fuera de control correspondían a la temporada de vacaciones de fin de año, lo cual afectó la calidad de respuesta a las solicitudes de los clientes, tanto en el funcionamiento como en el cumplimiento.
. Haciendo una revisión detallada del proceso se logró establecer que las causas para que éste se encontrara fuera de control correspondían a la temporada de vacaciones de fin de año, lo cual afectó la calidad de respuesta a las solicitudes de los clientes, tanto en el funcionamiento como en el cumplimiento.
6. CONCLUSIONES
Se propone la carta MNP para vigilar el comportamiento de un proceso para variables tipo atributos correlacionados, pues posee un ARL adecuado tanto en control como fuera de control. Particularmente fuera de control, cuando las contaminaciones son positivas o negativas en la mayoría de las simulaciones detecta primero una desviación pequeña de la media del proceso. Esta carta también presenta un desempeño similar en todos los escenarios de simulación, lo que la hace robusta para medir si un proceso de esta naturaleza está o no en control estadístico.
Las cartas AN y 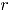 presentan variaciones significativas en cuanto a su rendimiento cuando las condiciones de simulación cambian, lo cual las hace poco confiables a la hora de determinar de manera temprana si un proceso se encuentra fuera de control. Si se compara el desempeño de las técnicas AN y
presentan variaciones significativas en cuanto a su rendimiento cuando las condiciones de simulación cambian, lo cual las hace poco confiables a la hora de determinar de manera temprana si un proceso se encuentra fuera de control. Si se compara el desempeño de las técnicas AN y 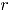 se puede concluir que son similares cuando la contaminación se da en dirección positiva y el tamaño de submuestra favorece a la aproximación de la distribución binomial a la normal (Caso 1). Cuando se observan los resultados del ejemplo aplicado, se ratifican las conclusiones del estudio de simulación, pues a pesar de que tanto la carta AN como la MNP detectan los puntos fuera de control, la técnica MNP presenta los puntos fuera de control más alejados de los límites de control.
se puede concluir que son similares cuando la contaminación se da en dirección positiva y el tamaño de submuestra favorece a la aproximación de la distribución binomial a la normal (Caso 1). Cuando se observan los resultados del ejemplo aplicado, se ratifican las conclusiones del estudio de simulación, pues a pesar de que tanto la carta AN como la MNP detectan los puntos fuera de control, la técnica MNP presenta los puntos fuera de control más alejados de los límites de control.
REFERENCIAS
[1] LARPKIATTAWORN, S. A Neural Network Approach for Multi-Attribute Process Control with Comparison of Two Current Techniques and Guidelines for Practical Use, Doctoral Dissertation, University of Pittsburgh, 2003. [ Links ]
[2] LU, X. S., XIE, M., GOH, T. N. AND LAI, C. D. Control Chart for Multivariate Attribute Processes, International Journal of Production Research, 36(12), 3477-3489, 1998. [ Links ]
[3] ZERTUCHE, F., CANTU, M. AND PIÑA, M. Sistema de Control Multivariado no Paramétrico de Procesos". Cultura Ciencia y Tecnología, 21(4), 11-18, 2007. [ Links ]
[4] LIU, R. Control Chart for Multivariate Processes. Journal of the American Statistical Association, 90(432), 1380-1387, 1995. [ Links ]
[5] PATEL, H. I. Quality Control Methods for Multivariate Binomial and Poisson Distributions, Technometrics, 15(1), 103-112, 1973. [ Links ]
[6] SULLIVAN, J. H. AND WOODALL, W. H. A Comparison of Multivariate Control Charts for Individual Observations, Journal of Quality Technology, 28(4), 398-408, 1996. [ Links ]
[7] KOCHERLAKOTA, S., AND KOCHERLAKOTA, K. Bivariate Discrete Distributions, Marcel Dekker, New York, 1992. [ Links ]
[8] MARSHALL, A. W. AND OLKIN, I. A Family of Bivariate Distributions by the Bivariate Bernoulli Distribution, Journal of the American Statistical Association, 80(390), 332-338, 1985. [ Links ]
[9] OSPINA, C. Control Multivariado de Procesos con Variables Binomiales Bivariadas, Tesis de Maestría, Posgrado en Estadística. Universidad Nacional, Medellín, 2009. [ Links ]
[10] LIU, R. AND SINGH, K. A Quality Index Based On Data Depth and Multivariate Rank Tests, Journal of the American Statistical Association, 88(421), 252-260, 1993. [ Links ]
[11] HAMURKAROGLU, C., MERT, M. AND SAYKAN, Y. Nonparametric Control Charts Based on Mahalanobis Depth, Hacettepe Journal of Mathematics and Statistics, 33, 57-67, 2004. [ Links ]
[12] ONG, S. H. The Computer Generation of Bivariate Binomial Variables with Given Marginals and Correlation, Communications in Statistics - Simulation and Computation, 21(2), 285-299, 1992. [ Links ]














