Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.77 no.162 Medellín Apr./June 2010
ANÁLISIS DE LA ESTABILIDAD ESPACIO-TEMPORAL DEL MÉTODO PETROV-GALERKIN EN CONTRACORRIENTE PARA LA ECUACIONES DE DIFUSIÓN-ADVECCIÓN
SPACE-TIME STABILITY ANALYSIS OF THE STREAMLINE UPWIND PETROV-GALERKIN METHOD FOR DIFUSSION-ADVECTION EQUATIONS
DIEGO GARZÓN
Profesor Asociado Universidad Nacional de Colombia, dagarzona@bt.unal.edu.co
CARLOS GALEANO
Profesor Asistente Universidad Nacional de Colombia, chgaleanou@unal.edu.co
JUAN MANTILLA
Profesor Asistente Universidad Nacional de Colombia, jmmantillag@unal.edu.co
Recibido para revisar Octubre 17 de 2008, aceptado Julio 17 de 2009, versión final Agosto 17 2009
RESUMEN: El presente artículo analiza la estabilidad espacial y temporal de una solución numérica de la ecuación de difusión-advección, a través del método de Petrov-Galerkin en contracorriente (SUPG), junto con una discretización temporal Backward-Euler. En la primera parte del artículo se plantean los conceptos fundamentales de la técnica de estabilización espacial SUPG para dos dimensiones y posteriormente se presentan las consideraciones empleadas para la discretización temporal. A continuación se trata la metodología y las expresiones necesarias para la implementación computacional del método. Se analizan dos casos de estudio en los cuales se compara la estabilidad espacial y temporal de la solución implementada, con la obtenida por medio de la aproximación convencional Bubnov-Galerkin. Se emplea el error en norma de energía para analizar la estabilidad de las aproximaciones obtenidas. Videos y gráficas adicionales de los problemas presentados en este artículo pueden ser descargados de www.gnum.unal.edu.co
PALABRAS CLAVE: Petrov-Galerkin, Backward-Euler, Estabilización, Difusión, Advección
ABSTRACT: This article analyzes the space and temporal stability of a numerical solution of the diffusion-advection equation through the streamline upwind Petrov-Galerkin Method (SUPG), along with a Backward-Euler temporal discretization. In the first part the fundamental concepts of the SUPG technique for space stabilization in two dimensions, and the temporal discretization considerations are presented. Next the methodology and necessary expressions for computer implementation of the method are treated. Two cases of study are developed in which the space and temporal stability of the implemented solution are compared with those obtained by means of the conventional Bubnov-Galerkin approach. The error in the energy norm is used to analyze the stability of the obtained results. Videos and additional graphs of the problems in this article can be downloaded from www.gnum.unal.edu.co.
KEYWORDS: Petrov-Galerkin, Backward-Euler, Stabilization, Diffusion, Advection
1. INTRODUCCIÓN
Aunque la formulación convencional de elementos finitos, o método de Bubnov-Galerkin, resulta útil y adecuada para el tratamiento de muchos problemas de la ingeniería, especialmente en el campo de la mecánica de sólidos, presenta problemas de estabilidad en la aproximación alcanzada cuando en la ecuación diferencial aparecen operadores no autoadjuntos, tal como el término advectivo en la ecuación (1).
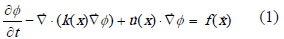
En esta última expresión, denominada ecuación de difusión-advección,  es la función de campo escalar a encontrar,
es la función de campo escalar a encontrar,  es el coeficiente difusivo,
es el coeficiente difusivo,  es el campo de velocidad asociado al proceso advectivo y
es el campo de velocidad asociado al proceso advectivo y 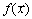 es la función de generación.
es la función de generación.
Este término advectivo, bajo la formulación convencional (Bubnov-Galerkin), tiene un efecto desestabilizador de la matriz de rigidez, introduciendo asimetría en la misma y produciendo oscilaciones falsas en la aproximación alcanzada, tal como se muestra en la Figura 1 para un problema unidimensional.
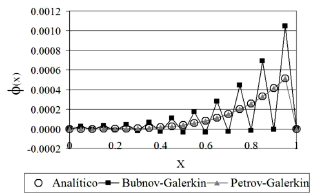
Figura 1. Falsas oscilaciones mostradas por la aproximación alcanzada con el método Bubnov-Galerkin
Figure 1. Spurious oscillations showed in Bubnov-Galerkin approximation method
La eliminación de estas oscilaciones o estabilización de la solución, se logra regresando el carácter simétrico a la matriz de rigidez, lo cual puede ser logrado empleando diversos métodos, entre los cuales se puede citar el método de las líneas de características [1], el método de cálculo finito [2], los métodos de fraccionamiento [3-4], el método de mínimos cuadrados de Galerkin [5] y el método Petrov-Galerkin de contracorriente (Streamline Upwind Petrov-Galerkin, SUPG) [6].
El SUPG se basa en la modificación de las funciones de ponderación, de manera que se otorgue mayor peso a la información de los nodos ubicados aguas arriba, por encima de los nodos ubicados aguas abajo, lo que es equivalente a emplear un método de diferencias finitas descentradas [7].
El presente artículo analiza la estabilidad espacial y temporal de la solución a la ecuación (1), empleando la técnica SUPG para la solución espacial y el método Backward-Euler en la dimensión temporal. En la primer parte del texto se exponen los fundamentos de la técnica SUPG para problemas bidimensionales, y posteriormente se presentan las consideraciones asociadas con la discretización temporal. Se presentan dos ejemplos de advección dominante y se analiza la estabilidad de la aproximación alcanzada en cada uno de ellos para diferentes mallas.
2. EL MÉTODO SUPG UNIDIMENSIONAL
En problemas unidimensionales la estabilización con el método de Petrov-Galerkin puede ser alcanzada adicionando un término perturbador a la función de peso estándar (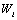 ), tal como se muestra en (2) [7]:
), tal como se muestra en (2) [7]:
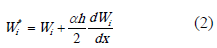
donde 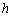 es el tamaño característico del elemento y
es el tamaño característico del elemento y 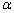 es un parámetro de perturbación positivo calculado con (3) [8-10].
es un parámetro de perturbación positivo calculado con (3) [8-10].
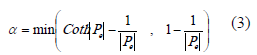
En esta última expresión, en la cual 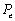 es el número adimensional de Peclet definido como
es el número adimensional de Peclet definido como 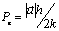 , se observa que la función de peso solo debe ser perturbada si
, se observa que la función de peso solo debe ser perturbada si 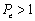 . En otras palabras, para valores inferiores en el número de Peclet la formulación SUPG lleva al planteamiento convencional de Bubnov-Galerkin. El término adicionado a la función de peso original en (2) modifica las funciones de ponderación
. En otras palabras, para valores inferiores en el número de Peclet la formulación SUPG lleva al planteamiento convencional de Bubnov-Galerkin. El término adicionado a la función de peso original en (2) modifica las funciones de ponderación 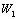 y
y 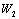 , tal como lo muestra la Figura 2, reduciendo el área bajo la curva de la función de peso
, tal como lo muestra la Figura 2, reduciendo el área bajo la curva de la función de peso 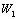 , al mismo tiempo que se aumenta el valor de la integral de
, al mismo tiempo que se aumenta el valor de la integral de 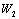 a lo largo del elemento. Esta modificación sobre
a lo largo del elemento. Esta modificación sobre 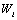 logra sobrestimar el valor de los coeficientes
logra sobrestimar el valor de los coeficientes 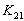 por encima de los coeficientes
por encima de los coeficientes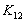 , en la ecuación de ensamble (4) de un nodo interno
, en la ecuación de ensamble (4) de un nodo interno  , la cual es obtenida a partir del sistema de ecuaciones (5).
, la cual es obtenida a partir del sistema de ecuaciones (5).
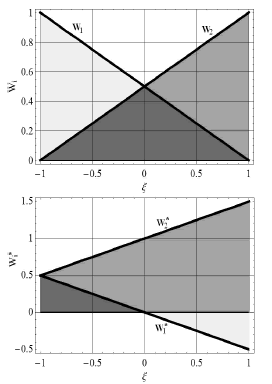
Figura 2. Funciones de peso originales (arriba) y modificadas con la expresión (1) (abajo)
Figure 2. Original weight functions (above) and modified weight functions with expression (1) (bottom)
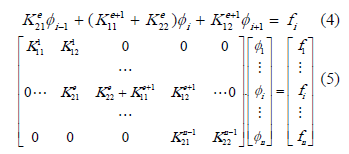
Para el anterior sistema de ecuaciones, los términos de la matriz de rigidez 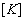 de un elemento
de un elemento 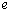 , calculados de acuerdo con el método SUPG unidimensional, están definidos por medio de la expresión (6) [7].
, calculados de acuerdo con el método SUPG unidimensional, están definidos por medio de la expresión (6) [7].
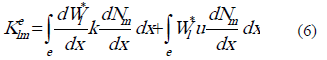
En esta última expresión 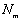 son funciones de forma empleadas en una aproximación por tramos convencional, como la planteada en (7).
son funciones de forma empleadas en una aproximación por tramos convencional, como la planteada en (7).
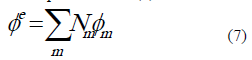
De forma análoga, los términos del vector 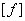 para un elemento
para un elemento 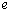 se definen de acuerdo con (8) [7].
se definen de acuerdo con (8) [7].
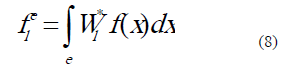
El uso de las expresiones (6) y (8), en la ecuación (4), permite llegar a la ecuación de ensamble estabilizada (9).
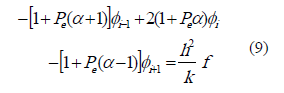
La formulación del problema unidimensional resulta en extremo valiosa para el análisis de la corrección impuesta por el método SUPG. Sin embargo, el planteamiento de esta técnica en problemas en dos o tres dimensiones requiere algunas consideraciones adicionales.
3. EL MÉTODO SUPG EN DOS DIMENSIONES
Se puede verificar fácilmente como la ecuación de ensamble unidimensional (9), alcanzada con la estabilización SUPG, puede ser construida de otra forma, partiendo de un planteamiento Bubnov-Galerkin y aumentando artificialmente el término difusivo, tal como se plantea en (10) [7].
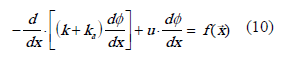
donde 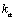 es el término difusivo incluido para estabilizar la solución y el cual se define como
es el término difusivo incluido para estabilizar la solución y el cual se define como 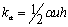 . Esta interpretación del método SUPG, resulta especialmente útil para la generalización de la técnica a problemas en dos o tres dimensiones. De esta forma, así como en problemas unidimensionales, la modificación de las funciones de peso es equivalente a adicionar un término difusivo adicional que actúa en la dirección del flujo, para problemas con una o dos dimensiones adicionales, se debe garantizar que el efecto de la difusión artificial actúe contrarrestando el efecto advectivo, el cual solo opera en la dirección de la velocidad
. Esta interpretación del método SUPG, resulta especialmente útil para la generalización de la técnica a problemas en dos o tres dimensiones. De esta forma, así como en problemas unidimensionales, la modificación de las funciones de peso es equivalente a adicionar un término difusivo adicional que actúa en la dirección del flujo, para problemas con una o dos dimensiones adicionales, se debe garantizar que el efecto de la difusión artificial actúe contrarrestando el efecto advectivo, el cual solo opera en la dirección de la velocidad 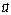 .
.
De acuerdo con este planteamiento, una perturbación sobre la función de forma, como la escrita en la ecuación (11), solo logra estabilizar el efecto advectivo en la dirección 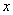 . De forma análoga se podría perturbar la función de ponderación para estabilizar la advección en la dirección
. De forma análoga se podría perturbar la función de ponderación para estabilizar la advección en la dirección 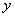 , como se muestra en (12).
, como se muestra en (12).
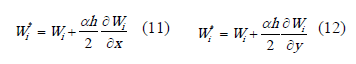
De esta forma, para lograr estabilizar la solución en la dirección de una velocidad bidimensional, se requiere ponderar las perturbaciones planteadas en (11) y (12), tal como se muestra en (13) [11-12].
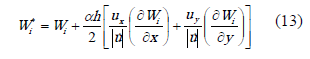
donde 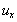 y
y 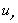 son las componentes de la velocidad en las direcciones globales
son las componentes de la velocidad en las direcciones globales 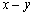 , y
, y 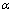 es el coeficiente de perturbación calculado de acuerdo con (3), empleando el valor de la norma de la velocidad y una dimensión característica
es el coeficiente de perturbación calculado de acuerdo con (3), empleando el valor de la norma de la velocidad y una dimensión característica 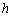 como la mostrada en la Figura 3.
como la mostrada en la Figura 3.
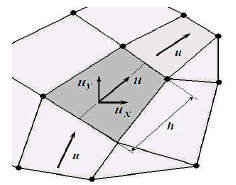
Figura 3. Línea de corriente al interior de un elemento bidimensional
Figure 3. Streamline inside a bidimensional element
Tomando la expresión (1) y aplicando el método de los residuos ponderados se obtiene la expresión (14).
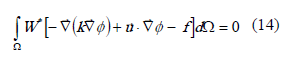
Al aplicar el teorema de Green sobre la anterior ecuación se logra llegar a la forma debilitada de la ecuación de residuos ponderados (15).
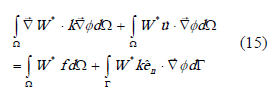
donde 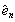 es el vector normal al borde de flujo o borde de Neumman. Empleando ahora aproximaciones por tramos del tipo
es el vector normal al borde de flujo o borde de Neumman. Empleando ahora aproximaciones por tramos del tipo 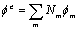 , así como la función de peso
, así como la función de peso
modificada (13), se llega al sistema de ecuaciones mostrado en (16).
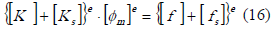
en donde 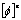 es el vector de valores nodales del elemento, en tanto que los demás términos se definen de acuerdo con (17), (18), (19) y (20).
es el vector de valores nodales del elemento, en tanto que los demás términos se definen de acuerdo con (17), (18), (19) y (20).
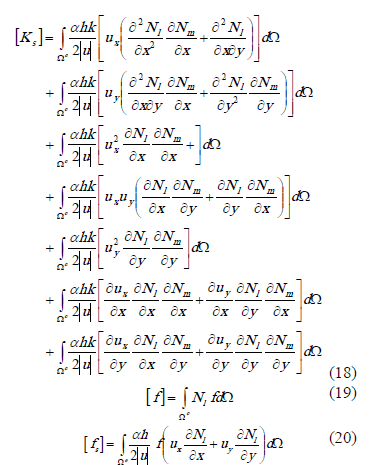
En las expresiones (17) a (20), 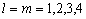 para un elemento cuadrilátero lineal.
para un elemento cuadrilátero lineal.
4. DISCRETIZACIÓN TEMPORAL
Para incorporar la dimensión temporal al problema de la ecuación de difusión-advección planteado previamente, se emplea una discretización temporal del tipo [13]:
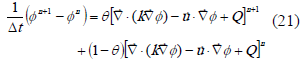
de modo que para 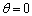 se llega a un planteamiento totalmente explícito y condicionalmente estable (Forward-Euler), como la descrita en (22).
se llega a un planteamiento totalmente explícito y condicionalmente estable (Forward-Euler), como la descrita en (22).
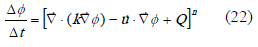
Así mismo, para 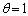 se obtiene el planteamiento implícito de la ecuación (23), denominado normalmente esquema Backward-Euler.
se obtiene el planteamiento implícito de la ecuación (23), denominado normalmente esquema Backward-Euler.
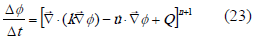
Por último, si 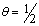 , se llega a un planteamiento semi-implícito denominado Crank-Nicolson y definido en la expresión (24).
, se llega a un planteamiento semi-implícito denominado Crank-Nicolson y definido en la expresión (24).
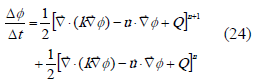
Aplicando el método de los residuos ponderados a la ecuación (23), y una discretización espacial convencional como en (7), se obtiene la expresión (25).
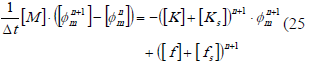
en esta última ecuación, la matriz 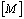 se define como:
se define como:
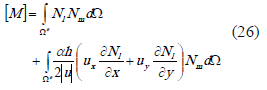
5. EXPERIMENTACIÓN NUMÉRICA
La implementación de la solución numérica de los casos presentados a continuación se realizó empleando el lenguaje de programación FORTRAN. Se definirán los siguientes casos:
5.1 Caso 1: Movimiento convectivo de una función gaussianaEste ejemplo, desarrollado entre otros autores por Wang [14], esta definido por la ecuación diferencial (27), para un dominio
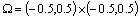 .
. 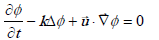
con 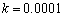 y un campo de velocidad rotacional
y un campo de velocidad rotacional 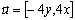 . Las condiciones de borde definidas para las cuatro fronteras del problema, son condiciones de Dirichlet homogéneas, en tanto que las condiciones iniciales están definidas por la expresión (28), con
. Las condiciones de borde definidas para las cuatro fronteras del problema, son condiciones de Dirichlet homogéneas, en tanto que las condiciones iniciales están definidas por la expresión (28), con 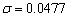 . La solución analítica del problema se plantea en la expresión (29).
. La solución analítica del problema se plantea en la expresión (29).
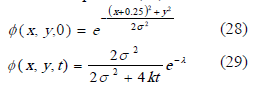
en esta última expresión:
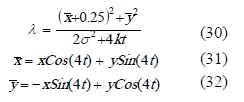
Este problema se caracteriza por tener tanto zonas de convección dominante, ubicadas cerca de los bordes del problema, como zonas de difusión dominante, ubicadas en la región cercana al centro del dominio. Estas zonas están definidas y no cambian en el tiempo, dado que el coeficiente de difusión y el campo de velocidades no son función de esta variable.
En las Figuras 4, 5 y 6 se muestran los resultados obtenidos en diferentes valores de tiempo, tanto con la formulación convencional (gráficas del lado izquierdo), como con la formulación estabilizada SUPG (gráficas del lado derecho). Ambos planteamientos se combinaron con una discretización temporal Backward-Euler empleando pasos de tiempo 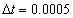 y un tiempo final
y un tiempo final 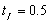 .
.
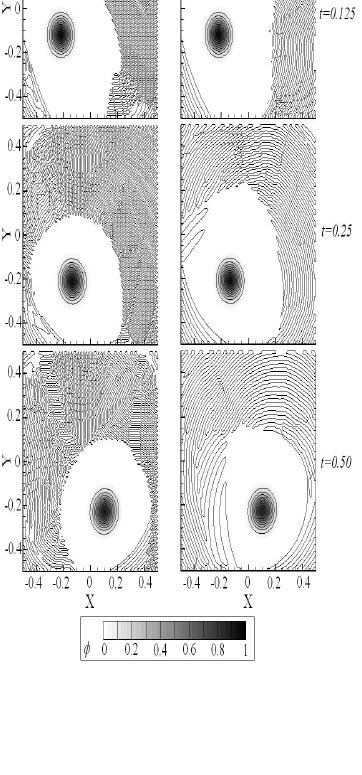
Figura 4. Soluciones transitorias obtenidas para el caso de estudio 1 empleando 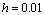
Figure 4. Transient solutions for the case where 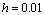
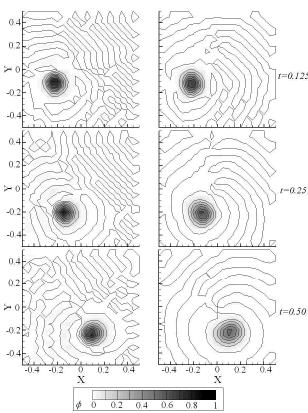
Figura 5. Soluciones transitorias obtenidas para el caso de estudio 1 empleando 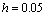
Figure 5. Transient solutions for the case where 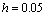
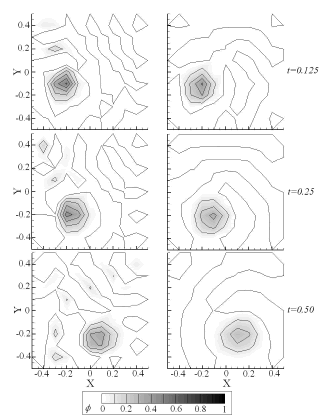
Figura 6. Soluciones transitorias obtenidas para el caso de estudio 1 empleando 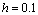
Figure 6. Transient solutions for the case where 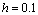
Para la primera malla, formada por 10000 elementos (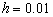 , Figura 4), se obtiene un número máximo de Peclet igual a 141, ubicado en los vértices del dominio, el cual decrece linealmente a medida que se esta más cerca del centro del cuadrado, alcanzando un valor mínimo de cero en este punto. Se observa que las dos soluciones (Bubnov y Petrov) son similares en cuanto a magnitud y desplazamiento de la función gaussiana. Sin embargo se presentan, en la solución Bubnov-Galerkin, pequeñas inestabilidades tal como se puede esperar debido a los altos valores de Peclet (
, Figura 4), se obtiene un número máximo de Peclet igual a 141, ubicado en los vértices del dominio, el cual decrece linealmente a medida que se esta más cerca del centro del cuadrado, alcanzando un valor mínimo de cero en este punto. Se observa que las dos soluciones (Bubnov y Petrov) son similares en cuanto a magnitud y desplazamiento de la función gaussiana. Sin embargo se presentan, en la solución Bubnov-Galerkin, pequeñas inestabilidades tal como se puede esperar debido a los altos valores de Peclet (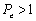 ). Estas inestabilidades se evidencian en la irregularidad de las líneas de contorno de las gráficas de la primera columna en la Figura 4.
). Estas inestabilidades se evidencian en la irregularidad de las líneas de contorno de las gráficas de la primera columna en la Figura 4.
Dichas inestabilidades crecen conforme se aumenta el tamaño de los elementos, es decir a medida que se aumenta el número de Peclet, tal como se observa en la Figura 5 (malla con 400 elementos, 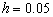 ), y especialmente en la Figura 6 (malla con 100 elementos,
), y especialmente en la Figura 6 (malla con 100 elementos, 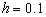 ), en donde debido a los altos valores de
), en donde debido a los altos valores de 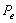 (máximo cercano a 1400), las oscilaciones alcanzan a tener valores comparables con la altura de la función gaussiana. No obstante, en este último caso la solución que se alcanza empleando SUPG no exhibe oscilaciones y aún se conservan las líneas de contorno suaves en la gráfica.
(máximo cercano a 1400), las oscilaciones alcanzan a tener valores comparables con la altura de la función gaussiana. No obstante, en este último caso la solución que se alcanza empleando SUPG no exhibe oscilaciones y aún se conservan las líneas de contorno suaves en la gráfica.
La Figura 7 muestra la variación del error en norma de energía a lo largo del tiempo, para las diferentes mallas empleadas, utilizando la solución convencional. La Figura 8, muestra de forma análoga, la variación del mismo error para la solución estabilizada con SUPG.
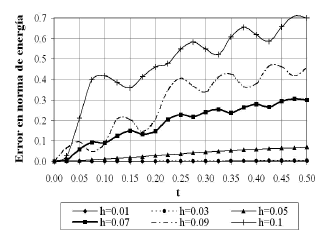
Figura 7. Variación del error en norma de energía a lo largo del tiempo para la solución Bubnov-Galerkin.
Figure 7. Energy norm error variation in time for the Bubnov-Galerkin solution
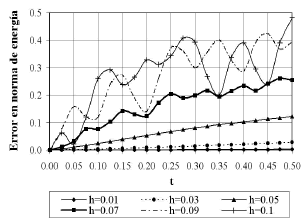
Figura 8. Variación del error en norma de energía a lo largo del tiempo para la solución SUPG
Figure 8. Energy norm error variation in time for the SUPG solution
Como se observa en las Figuras 7 y 8, se presentan oscilaciones en el valor del error a lo largo del tiempo, tanto para el método de elementos finitos convencional, como para el método estabilizado (SUPG). Este comportamiento, que se presenta únicamente con las mallas más gruesas, muestra que la técnica Backward-Euler de discretización temporal, no siempre se puede considerar condicionalmente estable y requiere, para las condiciones de solución impuestas, una malla con tamaño promedio inferior a 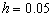 con el fin de alcanzar una estabilidad en la dimensión temporal.
con el fin de alcanzar una estabilidad en la dimensión temporal.
5.2 Caso 2: Movimiento convectivo de un frente de onda
El ejemplo, tomado de [15], modela la propagación de un frente de onda dentro de un dominio cuadrado 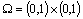 . El problema esta definido por medio de la ecuación (27), para una constante
. El problema esta definido por medio de la ecuación (27), para una constante 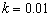 y un campo de velocidad definido por el vector
y un campo de velocidad definido por el vector 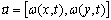 , en donde:
, en donde:
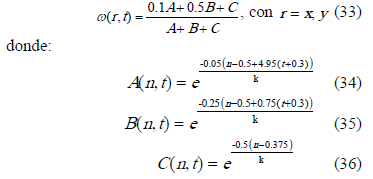
Las condiciones de borde definidas para este ejemplo son condiciones de Neumman homogéneas, en tanto que las condiciones iniciales están dadas por la ecuación (37).
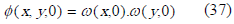
El ejemplo resulta interesante porque el campo de velocidades asociado al término advectivo es variable en el tiempo y en el espacio, formando una zona predominantemente advectiva que crece, a la vez que la zona de difusión dominante se reduce, como se muestra en la Figura 9. Esta condición exige de la técnica numérica empleada una mayor capacidad de estabilización tanto en la dimensión espacial, como en la temporal.
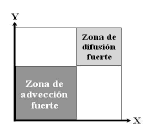
Figura 9. Distribución de las zonas predominantemente advectivas y difusivas para el segundo caso de análisis
Figure 9. Advective and diffusive zone distribution for the second case
Los resultados obtenidos en este ejemplo se muestran en las Figuras 10, 11 y 12 para diferentes los diferentes instantes de tiempo, considerando tanto la formulación convencional (gráficas de la izquierda), como el método SUPG (gráficas de la derecha). Ambos planteamientos se combinaron con una discretización temporal Backward-Euler empleando pasos de tiempo 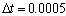 y un tiempo final
y un tiempo final 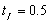 .
.
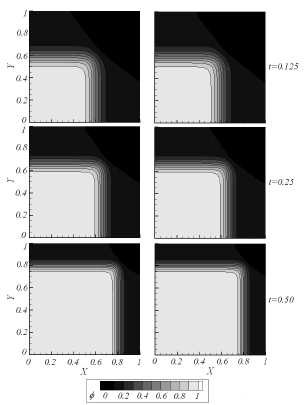
Figura 10. Soluciones transitorias obtenidas para el caso de estudio 2 empleando 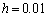
Figure 10. Transient solutions for the case where 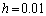

Figura 11. Soluciones transitorias obtenidas para el caso de estudio 2 empleando 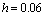
Figure 11. Transient solutions for the second case where 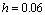
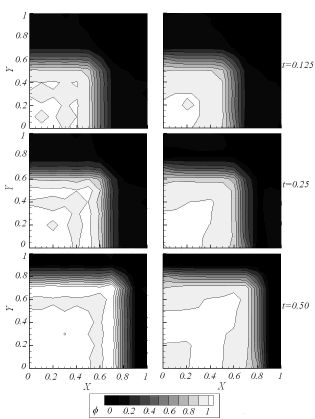
Figura 12. Soluciones transitorias obtenidas para el caso de estudio 2 empleando 
Figure 12. Transient solutions for the second case where 
Se observa como con la malla más fina, formada por 10000 elementos ( , Figura 10), no hay diferencias significativas en las aproximaciones alcanzadas por las dos técnicas (Bubnov y Petrov). Esto se explica teniendo en cuenta que el número de
, Figura 10), no hay diferencias significativas en las aproximaciones alcanzadas por las dos técnicas (Bubnov y Petrov). Esto se explica teniendo en cuenta que el número de 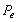 en la zona de advección dominante, en donde se requiere la estabilización, es igual a 0.75 (
en la zona de advección dominante, en donde se requiere la estabilización, es igual a 0.75 (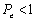 ).
).
Para la segunda malla mostrada, construida con 289 elementos (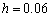 , Figura 11), el número de
, Figura 11), el número de 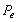 en la zona de advección dominante se eleva a 4.5 (
en la zona de advección dominante se eleva a 4.5 (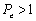 ) y se empiezan a encontrar oscilaciones espurias con la aproximación convencional. Para el mismo caso la solución SUPG no presenta inestabilidades y la aproximación alcanzada es similar a la encontrada con la malla más fina. Estas oscilaciones se hacen mucho más evidentes empleando una malla más gruesa
) y se empiezan a encontrar oscilaciones espurias con la aproximación convencional. Para el mismo caso la solución SUPG no presenta inestabilidades y la aproximación alcanzada es similar a la encontrada con la malla más fina. Estas oscilaciones se hacen mucho más evidentes empleando una malla más gruesa 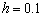 (Figura 12). Con esta malla el número
(Figura 12). Con esta malla el número 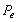 es igual a 7.5 en la zona de altamente advectiva, y se observa, para esta zona, un incremento en la amplitud de las oscilaciones de la aproximación alcanzada con el método convencional Bubnov-Galerkin.
es igual a 7.5 en la zona de altamente advectiva, y se observa, para esta zona, un incremento en la amplitud de las oscilaciones de la aproximación alcanzada con el método convencional Bubnov-Galerkin.
La Figura 13 muestra la variación a lo largo del tiempo del error en la norma de energía encontrado con las diferentes mallas empleadas con la solución convencional. La Figura 14, muestra de forma análoga, la variación del mismo error para la solución con SUPG.
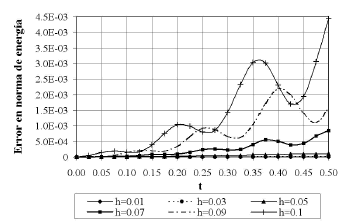
Figura 13. Variación del error en norma de energía a lo largo del tiempo para la solución Bubnov-Galerkin del caso 2
Figure 13. Energy norm error variation in time for the Bubnov-Galerkin solution for the second case
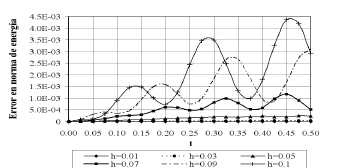
Figura 14. Variación del error en norma de energía a lo largo del tiempo para la solución Petrov-Galerkin del caso 2
Figure 14. Energy norm error variation in time for the SUPG solution for the second case
Se observa nuevamente en las Figuras 13 y 14, al igual que en las Figuras 7 y 8 del ejemplo anterior, una inestabilidad temporal asociada con el método de discretización Bacward-Euler empleado. Es de notar que independientemente del método de discretización espacial utilizado (Bubnov o Petrov), se requiere una malla con tamaño promedio inferior a 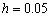 (dado el valor de incremento temporal empleado
(dado el valor de incremento temporal empleado 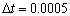 ) para lograr un comportamiento estabilizado en la dimensión temporal.
) para lograr un comportamiento estabilizado en la dimensión temporal.
6. CONCLUSIONES
Desde el punto de vista espacial se observa que la estabilización SUPG permite eliminar las oscilaciones espurias de la aproximación por elementos finitos. Estas irregularidades en la solución aparecen en las regiones con números de Peclet mayores a la unidad, y su magnitud aumenta a medida que el valor adimensional 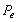 se incrementa, como por ejemplo con el empleo de mallas más gruesas.
se incrementa, como por ejemplo con el empleo de mallas más gruesas.
El método de estabilización implementado permite alcanzar soluciones adecuadas incluso para casos en los que el dominio espacial posee sub-zonas predominantemente difusivas y advectivas claramente definidas.
Se encontró que para ambos problemas, el error en la norma de energía en la dimensión espacio-temporal se comporta de forma similar tanto con la solución convencional, como con la aproximación estabilizada (SUPG). Esto se explica analizando el carácter espacial del método Petrov-Galerkin, el cual no consigue mejoras significativas en cuanto a la estabilización temporal. De esta forma se concluye que la componente más representativa de este error se presenta en el dominio temporal por la acumulación del mismo en cada paso de tiempo 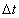 . Esta conclusión se ratifica al observar las gráficas del comportamiento del error en la norma de energía espacial, el cual muestra crecimiento a lo largo del tiempo, tanto para el método Bubnov-Galerkin, como para el método Petrov-Galerkin.
. Esta conclusión se ratifica al observar las gráficas del comportamiento del error en la norma de energía espacial, el cual muestra crecimiento a lo largo del tiempo, tanto para el método Bubnov-Galerkin, como para el método Petrov-Galerkin.
REFERENCIAS
[1] ZIENKIEWICZ, O., LÖHNER, R., MORGAN, K. AND NAKAZAWA, S. Finite Elements in Fluid mechanics- a decade of progress, Finite Elements in Fluids, 5, 1-26, 1984. [ Links ]
[2] OÑATE, E. DERIVATION of stabilized equations for numerical solution of advective diffusive transport and fluid flow problems, Computer Methods in Applied Mechanics and Enginnering, 151, 233-265, 1998. [ Links ]
[3] CHRISPELL, J., ERVIN, V. AND JENKINS, E. A fractional step ?-method for convection-diffusion problems, Journal of Mathematical Analysis and Applications, 333, 204-218, 2007. [ Links ]
[4] RENOU, S., PERRIER, M., DOCHAIN, D. And GENDRON, S. Solution of the convection-dispersion-reaction equation by a sequencing method, Computers and Chemical Engineering, 27, 615-629, 2003. [ Links ]
[5] HUGHES, T., FRANCA, L., HULBERT, G., JOHAN Z. AND SAKHIB, F. The Galerkin least square method for advective diffusion equations, Recent Developments in Computational Fluid Mechanics, AMD 94-ASME, 1988. [ Links ]
[6] ZIENKIEWICZ, O., GALLAGHER, R. AND HOOD, P. NEWTONIAN AND non-Newtonian viscous impompressible flow. Temperature inducedflows and finite elements solutions. The Mathematics of Finite Elements and Applications, Academic Press (ed.), 1975. [ Links ]
[7] ZIENKIEWICZ, O. AND TAYLOR, R. Finite Element Method Vo. 3, Butterworth-Heinemann College (ed.), 5-150, 2000.
[8] CHRISTIE, I., GRIFFITHS, D. AND ZIENKIEWICZ, O. Finite element methods for second order differential equations with significant first derivatives, International Journal for Numerical Methods in Engineering, 10, 1389-1396, 1976. [ Links ]
[9] GALEÃO, A., ALMEIDA, R., MALTA, S. AND LOULA, A. Finite element analysis of convection dominated reaction-diffusion problems, Applied Numerical Mathematics, 48, 205-222, 2004. [ Links ]
[10] TEZDUYAR , T. AND OSAWA, Y. FINITE element stabilization parameters computed from element matrices and vectors, Comput. Methods Appl. Mech. Engrg, 190, 411-430, 2000. [ Links ]
[11] HUGHES, T. AND BROOKS, A. A multidimensional upwind scheme with no crosswind diffusion, In Finite Element Method for Convection Dominated Flows (ASME), 34, 19-35, 1979. [ Links ]
[12] SHEU, T. AND SHIAH, H. The two-dimensional streamline upwind scheme for the convection-reaction equation, Int. J. Numer. Meth. Fluids, 35, 575-591, 2001. [ Links ]
[13] ASENSIO, M., AYUSO , B. AND SANGALLI, G. Coupling stabilized finite element methods with finite difference time integration for advection-diffusion-reaction problems, Comput. Methods Appl. Mech. Engrg, 196, 3475-3491, 2007. [ Links ]
[14] WANG, H., DAHLE, H., EWING, R., Espedal, M., Sharpley, R. and Man, S. An ELLAM scheme for advection-diffusion equations in two dimensions, SIAM J. Sci. Comput, 20, 6, 2160-2194, 1979. [ Links ]
[15] Berzins, M. Temporal error control for convection-dominated equations in two space dimensions, SIAM J. Sci. Comput, 16, 3, 558-580, 1995. [ Links ]














