Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.77 n.163 Medellín jul./set. 2010
NUMERICAL SIMULATION OF THIN LAYER COFFEE DRYING BY CONTROL VOLUMES
SIMULACIÓN NUMÉRICA DE SECADO DE CAFÉ EN CAPA DELGADA USANDO VOLÚMENES DE CONTROL
HÉCTOR J. CIRO-VELÁSQUEZ
Department of Agricultural and Food Engineering, UNAL- Sede Medellín, hjciro@unal.edu.co
LUIS C. ABUD-CANO
Mechanical Engineer, M.Sc, labud68@hotmail.com
LUIS. R. PÉREZ-ALEGRÍA
Department of Agricultural and Biosystems Engineering, University of Puerto Rico-Mayagüez Campus, luisr.perez1@upr.edu
Received for review May 21th, 2009, accepted September 8th, 2009, final version September, 24th, 2009
ABSTRACT: The thin layer drying model proposed by Sokhansanj and Bruce (1987) was implemented to model the drying process of parchment coffee beans. A computational model based on a control volume approach was developed to simulate the drying process of parchment coffee. A one dimensional transient analysis was implemented in the radial direction applied to a spherical coffee bean of equivalent radius. The results found that, even though the numerical value for the mass transfer coefficient is a small number (about of 10-7 m/sec), moisture content predictions were sensitive to this value. The predicted drying curve compared favorably with published results.
KEY-WORDS: Coffee, drying, numerical simulation, thin layer.
RESUMEN: El modelo de secado en capa delgada desarrollado por Sokhansanj y Bruce (1987) fue implementado para simular el secado de un grano de café pergamino. El modelo computacional fue definido en estado transitorio y unidimensional para una esfera de radio equivalente utilizando la técnica del volumen de control. Los resultados indicaron que el valor numérico del coeficiente de transferencia de masa es muy pequeño (orden de magnitud alrededor de 10-7 m/s) haciendo que la predicción del contenido de humedad sea muy sensible a este valor. Además, los resultados de la simulación mostraron que la predicción del modelo numérico fue favorablemente similar a los datos experimentales dados en la literatura.
PALABRAS CLAVES: Café, secado, simulación numérica, capa delgada.
1. INTRODUCTION
Worldwide, Colombia is the third coffee producing country and the first coffee producer of smooth coffees. To reach and maintain the status of the Colombian coffee, understanding of the impact of coffee drying and other stages of postharvest management has been fundamental.
Drying of grains has been a research-intensive area because of the complexity of the drying phenomenon and, consequently, modeling and simulation of the same needs the proper definition of the governing equations with boundary conditions, use of appropriate material properties and consideration of mechanical and chemical effects, when necessary [1-3].
Drying is the part of the postharvest process that is responsible for the removal of excess moisture to a level that is safe for long time storage without any impact to aroma or taste of the final beverage. Drying is a combination of heat and mass transfers that occurs simultaneously where moisture is removed by evaporation from the outer surface of the bean due to partial vapor pressure differential between the bean's and the air mass that surrounds it [4-6]. Drying could affect the physical appearance, the yield at hulling and the taste of the beverage [7]. Actually, dry parchment coffee is sold at final moisture content between 10 and 12% wet basis.
Coffee drying in deep beds is modeled using thin-layer models (thin-layer is the depth of three layers of coffee beans), one in top of the next until the depth of the bed is reached. Models build this way are able to predict and simulate the temperature and moisture profile under constant air flow [8-10]. Therefore, the accuracy of this modeling approach directly depends on the accuracy of the thin-layer drying model [11-14].
This paper describes a new implemented coffee drying simulation model based on heat conduction equation [15]. Upon validation the model can be used to design and optimization of deep bed dryers for parchment coffee beans.
2. THEORETICAL ANALYSIS
The general diffusion equation that describes moisture mass transfer in the bean is given by the equation:

Initial and boundary conditions for equation (1) are, respectively:
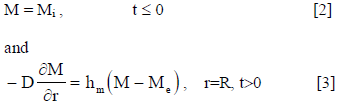
In convective drying, the grain's surface exchange heat with the surroundings as a result of convection, while the internal mass of the grain is heated by heat conduction. The general form of heat conduction equation that applies to grain drying can be written as:
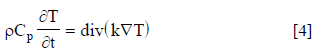
Boundary conditions for eq. (4) area based on 1) liquid moisture in the grain moves from the interior layer to the outer surface by diffusion and 2) moisture evaporates from the outer surface. The energy balance at the bean's surface can be written as:
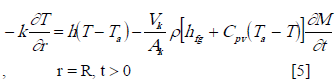
Eq. 5 implies that the energy transported by the air is used to evaporate moisture in the bean's surface and the rest to heat the internal layers of the bean. The initial condition for this process is:

Using the mass transfer condition in eq. (3), the boundary condition for the bean's temperature (eq. 5) can be simplified [16] to:
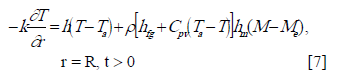
The set of equations described above represent heat and mass transfer in a coffee bean. These equations are tight together by the use of the derivative of the bean's moisture content and time (eq. 5) are solved to describe temperature and moisture profiles in a single coffee bean.
The thin layer coffee drying model developed here use the following assumptions: 1) the coffee bean is homogeneous and isotropic, 2) the bean is represented by an equivalent sphere which is defined as the ratio between bean's volume and surface area, 3) the bean is symmetrical with respect to its principal axis and temperature and moisture depend on the radial distance, r and time, t, 4) moisture evaporation takes place in the bean's surface, 5) initial temperature and moisture content are uniform, 6) temperature and moisture profiles are symmetrical during the drying process, 7) heat and mass transfer are pure diffusion within the bean and outside the bean are pure convection. There is not heat radiation, 8) bean's volume is assumed constant, there is no shrinkage or expansion of the bean during drying and 9) specific heat and thermal conductivity depend on the bean's moisture content. Diffusion coefficient and latent heat of vaporization depend on the bean's temperature and moisture content.
2.1 Numerical scheme
Under transient regime, heat and moisture transfer equations are non-linear. These equations have physical variables that depend on bean's moisture and temperature [17]. The set of equations were solved using the control-volume scheme [18]. In this scheme, each control-volume maintains mass conservation, energy and momentum. To apply this technique, the computational domain is divided in a known number of control-volumes that do not overlap and that each node of the grid is associated with one control volume. In each control volume, energy or mass balances are performed. Moisture and temperature variations follow a linear profile with respect to radial distance, r. The solution also uses an implicit scheme that assumes that the new value of the dependent variable (temperature or moisture) prevails constant during the time interval. As a result of this scheme, a set of algebraic equations are generated. The set of algebraic equations, one for each control volume, are solved using an iterative procedure. The coffee bean is represented by a sphere with an equivalent radius that is symmetrical with respect to the azimuthal coordinate φ. The solution model uses only an eighth of sphere. The model also assumes symmetry with respect to the zenith angle q. Therefore, the model offers solutions with respect to the polar coordinates; radial, r and time, t. Figure 1 shows the solution scheme for any zenith angle of the sphere. The plain in Fig. 1 is divided in N number of sub-regions with a node in the mid-radius of each sub-region, except for nodes 0 and N that are located in the center and the outer surface of the sphere, respectively. The energy and moisture mass balance for the central, intermediates and surface nodes a set of N+1 simultaneous algebraic equations are generated for N+1 X's unknowns. These set of equations are expressed in matrix form as:
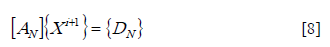
Where, X represents the bean's temperature or moisture, A and D are constants that depend mainly on physical and thermal properties of coffee beans and its geometry.
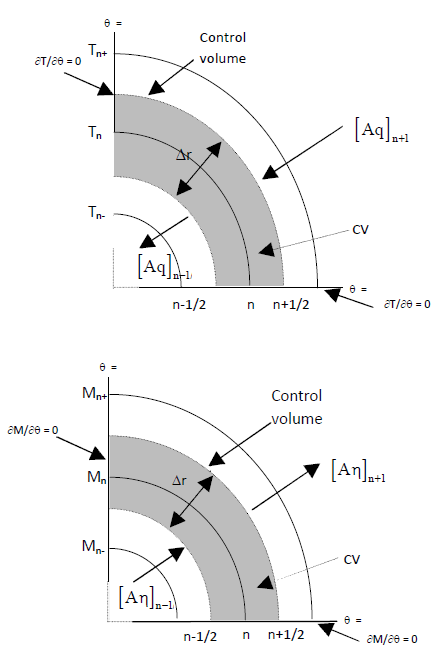
Figure 1. Control volume for heat and mass transfers within parchment coffee beans
The solution of the system of non-linear equations (eq. 8) gives the node's temperature and moisture content for each time interval during the drying process. Non-linearity comes from the fact that the thermal conductivity and the bean's specific heat depend on the grain moisture content; while the diffusion coefficient and the latent heat of vaporization depend on the bean's temperature and moisture content.
Assuming that the bean's density remains constant, the mean temperature or mass temperature and mean moisture content were determined using the following equations:
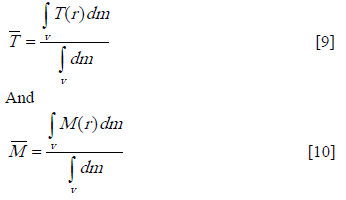
The solution of the matrix system of equation at each step was obtained by successive iterations. The implicit method was chosen because it is unconditionally stable. A banded matrix of unknowns was thus formed with the solution obtained using a standard iterative solver for the matrix. The moisture matrix was solved first and the change in the moisture from one iteration step to the next was substituted into the temperature boundary condition. This information was then transferred to the ‘D' matrix of the temperature equation and the conduction equation was solved. The numerical solution was coded in Fortran.
2.2 Thermo-physical Properties of Coffee
Thermal and physical properties of the coffee bean were taken from the literature: Diffusion coefficient [19], equilibrium moisture content and latent heat of vaporization [20]; equivalent radius, real density, thermal conductivity and specific heat [21]. Heat and mass transfer coefficients were calculated in this study.
The heat transfer coefficient was calculated using correlation for grains [15]:
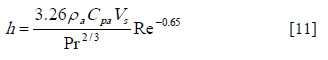
Initially, the mass transfer coefficient was estimated using the Chilton-Colburn analogy:
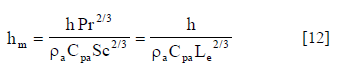
3. RESULTS AND DISCUSSION
3.1 Computational model
Convergence and stability of the model's solution scheme was studied by discretizing the domain (number of nodes) and the time-step and measuring its effect on estate variables (temperature and moisture). A robust model offers solutions that are independent of the discretization used and the time interval selected.
3.2 Effect of the nodal grid
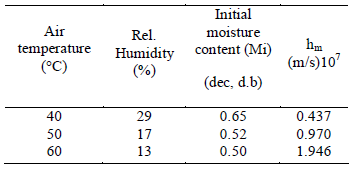
The effect of the nodal grid in the solution was measured by calculating coffee bean's moisture content for a 30-hr drying time with one second time-step. Reference [22] gives the drying operational conditions used in this study: Air drying temperature (Ta=40°C), relative humidity (RH=29%) and initial moisture content (Mi=0.65 decimal, d.b). Table 1 shows that the obtained mean bean's moisture is less than 0.5% between a 40 and 80 node's grid. Therefore, a 40 node grid was used in this study.
Table 1. Influence of mesh size on model's stability

3.3 Effect of time-step
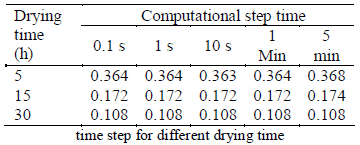
The solution model showed no sensitivity and no significant differences of the bean's moisture when the integration time was varied from 0.1 to 60 seconds (Table 2). Therefore a 60-sec integration time was used for the solution.
Table 2. Model stability according to computational time step for different drying time
3.4 Model's validation
Reference [22] presents the experimental data of coffee drying used to validate the model. Bean's moisture results using the mass transfer coefficient generated by the Chilton-Colburn analogy under predicts the bean's moisture during the entire drying process (Figure 2). Thus, the drying process occurs at a faster rate than observed; therefore, the mass transfer coefficient calculated using Chilton-Colburn is not appropriate for coffee beans.
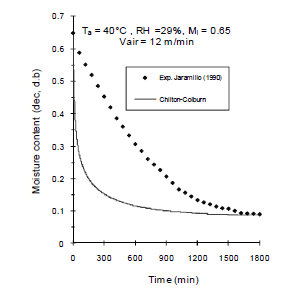
Figure 2. Simulated mean moisture content of parchment coffee bean using the Chilton-Colburn analogy (hm = 0.561x10-1 m/s)
The mass transfer coefficient was then calculated with the experimental data. A constant moisture loss is assumed for all phases of the drying process. During drying, moisture is only loss at the bean's surface; therefore, moisture migration within the bean is controlled by water loss at the bean's surface. The mathematical expression for moisture loss is:
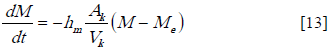
After integration and assuming "hm"; a time independent function, obtain:
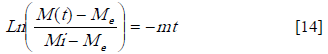
Thus, the graph of bean's moisture versus time should produce a straight line with slope m (Eq. 14). Hence, the mass transfer coefficient is given by:

In Figure 3 the mass transfer coefficient was varied to simulate the drying conditions. The prediction of the model improves for the initial 600 min (10 hr) of drying when the coefficient was reduced in 30% (hm=0.305x10-7 m/s) and worsen when the coefficient was increased in 30%. Regardless of the value of hm the model over estimates grain moisture at the final stages of drying. Although hm is a small number (Table 3), it controls the bean's moisture during drying.
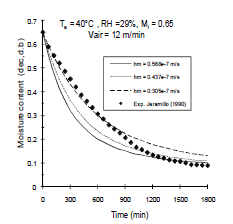
Figure 3. Simulated mean moisture content of parchment coffee bean to different heat mass transfer coefficients
A better estimate of the mass transfer coefficient was generated taking into account the time into drying and therefore the bean's moisture content with the following eqs.:
Table 3. Mass transfer coefficients calculated according to drying experimental conditions
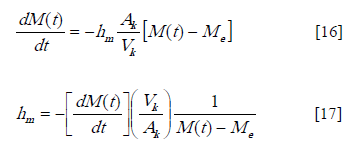
In these eqs., hm depend on the bean's moisture content, equilibrium moisture content and moisture ratio for every stage of the drying process (temperature, relative humidity and airflow velocity). Eq.(18) gives the final expression for hm according to drying conditions presented in Figure 4:
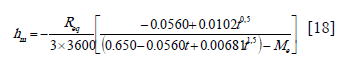
Updating hm during the drying process improved significantly model's predictions (Figures 4, 5 and 6). Further analysis of the results indicate that the bean's moisture equilibrium, Me developed in reference [20] and used in this study, is responsible for predicting higher bean's moisture contents at the end of the drying process [22].
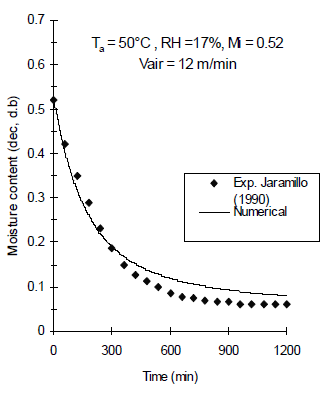
Figure 4. Simulated mean moisture content of parchment coffee beans using an experimental mass transfer coefficient changing with the drying time and drying conditions: air temperature ( 40°C), relative humidity (29%), initial moisture content (0.65) and air velocity (12 m/min)
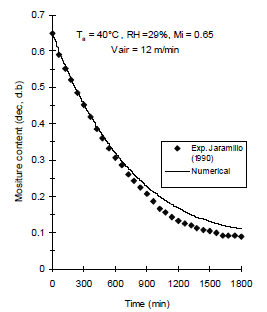
Figure 5. Simulated mean moisture content of parchment coffee beans using an experimental mass transfer coefficient changing with the drying time and drying conditions: air temperature ( 50°C), relative humidity (17%), initial moisture content (0.52) and air velocity (12 m/min)
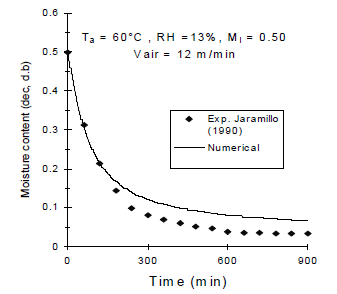
Figure 6. Simulated mean moisture content of parchment coffee bean using an experimental mass transfer coefficient changing with the drying time and drying conditions: air temperature ( 60°C), relative humidity (13%), initial moisture content (0.50) and air velocity (12
3.5 Bean's Temperature
Bean's interior and surface temperature increased during the first 15 min of simulation time (Figures 7A, B, C). The bean's mean and surface temperatures reached equilibrium temperature (air temperature) 20 min from initiation of drying and then remained constant during the rest of the process.
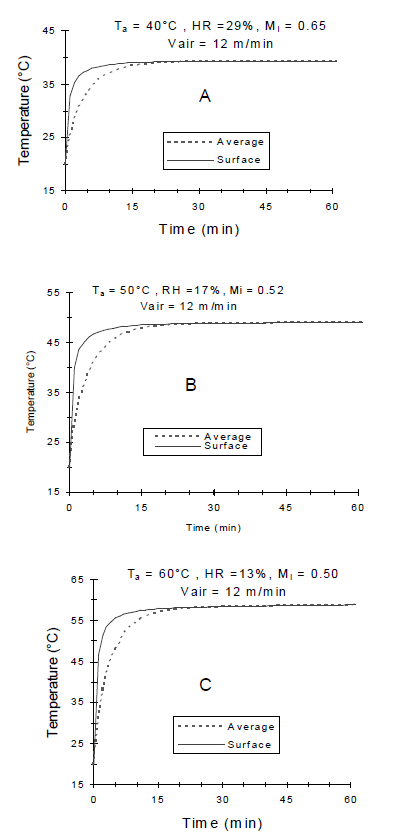
Figure 7. Simulated temperature of parchment coffee beans for different experimental drying conditions
A sharp increase in the mass average temperature prediction during the first few minutes of drying indicates the presence of large temperature gradients and therefore high levels of thermal stress during that period. Hence, rapid stabilization of the mass average temperature could have an effect on mass transfer [1]. The short time required for equilibrium temperature is documented [15, 23-24] but due to lack of temperature profile of coffee beans during drying this study could not validate this claim for coffee beans.
Practical application of thin-layer theory is limited because rarely coffee is dried in thin layers now days. Its importance lays in the fact that bean's temperature and moisture transfer is govern by thin-layer theory, therefore any improvement to the modeling of thin layer directly improves modeling of deep coffee drying. Thus, this paper provides a direct contribution to real application of coffee drying.
4. CONCLUSIONS
Thin-layer coffee drying was successfully modeled using the equation proposed by Sokhansanj and Bruce (1987). A key element that affected the accuracy of the model is the availability of relevant experimental data to generate thermophysicals parameters of coffee beans or any grain that are relevant to describe thermal and mass diffusion within the drying process. It was also found that the mass transfer coefficient is a very small number in the order of 10- 7 m s-1 but highly significnt to describe the process and very dependent on the time elapsed in drying process.
LIST OF SYMBOLS
Ak= Kernel superficial area, m2.
AN= Numerical matrix.
Cp= Specific heat, kJ/kg K.
Cpa= Air specific heat, kJ/kg K.
Cpv= Vapor specific heat, kJ/kg K.
D= Kernel diffusivity, m2/s.
DN= Matrix
h= Air-grain convective heat transfer coefficient, W/m2 K.
hfg=Latent heat vaporization of water, kJ/kg.
hm=Convective mass transfer coefficient, m/s.
k=Kernel thermal conductivity, W/m K.
Le= Lewis number
M= Kernel moisture content, decimal d.b.
Me= Equilibrium moisture content, decimal d.b.
Mi= Initial moisture content, decimal d.b.
Pr= Prandtl number.
r= radial coordinates.
R= Radius of the grain, m.
Re= Reynolds number.
Req= Equivalent radius, m.
RH= Relative humidity, %.
Sc= Schmidt number.
t= drying time, h.
T= Kernel temperature, ºC.
Ta= Air drying temperature, ºC.
Ti= Initial temperature, ºC.
Vk= Kernel Volume, m3.
Vs= Superficial air velocity, m/s.
X= Variables vector.
Greek Symbols
r= Kernel density, kg/m3.
ra= Air density, kg/m3.
REFERENCES
[1] IRUDAYARAJ, J., HAGHIGHI, K. AND STROSHINE, R. L. Finite element analysis of drying with application to cereal grains, J. Agric. Eng. Res., 53, 209-229, 1992. [ Links ]
[2] DUTTA, A. K. AND ZHANG. J. Porous media approach to heat and mass transfer in solid foods, ASAE Paper No. 99-3068. St. Joseph, Mich.: ASAE, 1999. [ Links ]
[3] RANJAN R., IRUDAYARAJ, J. AND JUN, S. A three-dimensional control volume approach to modeling heat and mass transfer in foods materials, Transactions of the ASAE 33, 209-229, 2001. [ Links ]
[4] SRIVASTAVA, V.K. AND JOHN, J. Deep bed grain drying modeling, Energy Conversion and Management 43, 1689-1708, 2002. [ Links ]
[5] ZIEGLER, TH. AND RICHTER, I.G. Analyzing deep-bed drying based on enthalpy-water content diagrams for air and grain, Computers and Electronics in Agriculture 26, 105-122, 2000. [ Links ]
[6] YADOLLAHINIA, A.R., OMID, M. AND RAFIEE, S. Design and fabrication of experimental dryer for studying agricultural products, International Journal of Agricultural & Biology 10, 61-65, 2008. [ Links ]
[7] AREGBA, A.W., SEBASTIAN, P. AND NADEAU, J.P. Stationary deep-bed drying: A comparative study between a logarithmic model and a non-equilibrium model, Journal of Food Engineering 77, 27-40, 2006. [ Links ]
[8] PABIS, S., JAYAS, D. S. AND CENKOWSKI, S. Grain drying: Theory and practice, John Wiley & Sons, 1998. [ Links ]
[9] FREIRE, F. B., BARROZO, M.A., SARTORI, D. AND FREIRE, J.T. Study of the drying kinetics in thin layer: fixed and moving bed, Drying Technology 23, 1451-1464, 2005. [ Links ]
[10] American Society of Agricultural and Biological Engineering (ASABE). Thin layer equation of agricultural crops: Standard S448.1, ASABE Standards, 2006. [ Links ]
[11] PARTI, M. Selection of mathematical models for drying grain in thin layer, J.Agric.Eng.Res. 54, 339-352,1993. [ Links ]
[12] BROOKER, D. B., BAKKER-ARKEMA, F.W. AND HALL, C.W. Drying and storage of grains and oilseeds, Springer, 1992. [ Links ]
[13] BALA, B.K. Drying and storage of cereal grains, Science Publishers, 1997. [ Links ]
[14] GARCÍA-PÉREZ, J.A., CARCEL, J.V., GARCÍA-ALVARADO, M.A. AND MULET, A. Simulation of grape stalk deep-bed drying, Journal of Food Engineering 90, 308-314, 2009. [ Links ]
[15] SOKHANSANJ, S. AND BRUCE, D. M. A conduction model to predict grain temperature in grain drying simulation, Transactions of the ASAE 30, 1181-1184, 1987. [ Links ]
[16] MIKETINAC, M. J., SOKHANSANJ, S. AND TUTEK, Z. Determination of heat and mass transfer coefficients in thin layer drying of grain, Transactions of the ASAE 35, 1853-1858, 1992. [ Links ]
[17] SANDER, A. Thin-layer drying of porous materials: Selection of the appropriate mathematical model and relationships between thin-layer models parameters, Chemical Engineering and Processing 46, 1324-1331, 2007. [ Links ]
[18] PATANKAR, S. V. Numerical Heat Transfer and Fluid Flow, Hemisphere Publishing Corp, 1980. [ Links ]
[19] MONTOYA E., OLIVEROS, C. AND ROA, G. 1990. Optimización operacional del secador intermitente de flujos concurrentes para café pergamino, Centro Nacional de investigaciones de Café, CENICAFE - Colombia 41, 19-33, 1990. [ Links ]
[20] TREJOS R., ROA, G. AND OLIVEROS, C. Humedad de equilibrio y calor latente de vaporización del café pergamino y del café verde, Centro Nacional de investigaciones de Café, CENICAFE- Colombia 40, 5-15, 1989. [ Links ]
[21] PEREZ-ALEGRÍA, L.R., CIRO-V., H.J. AND ABUD, L.C. Physical and thermal properties of parchment coffee bean, Transactions of the ASAE 44, 1721-1726, 2001. [ Links ]
[22] JARAMILLO B. G. Ecuación de capa delgada para café pergamino, Centro Nacional de investigaciones de Café, CENICAFE - Colombia 41, 103-113, 1990. [ Links ]
[23] FORTES, M. AND OKOS, M. R. A non-equilibrium thermodynamics approach to transport phenomenon in capillary porous bodies, Transactions of the ASAE 24, 756-760, 1981. [ Links ]
[24] IRUDAYARAJ, J. AND WU, Y. Numerical modeling of heat and mass transfer in starch systems, Transactions of the ASAE 42, 449- 455, 1999. [ Links ]














