Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.77 n.164 Medellín out./dez. 2010
MATRICES DE RIGIDEZ Y DE CARGA DE PRIMER Y SEGUNDO ORDEN DE UNA VIGA-COLUMNA ORTOTRÓPICA CON CONEXIONES SEMIRRÍGIDAS: I) TEORIA
FIRST AND SECOND ORDER STIFFNESS AND LOAD MATRICES OF AN ORTHOTROPIC BEAM COLUMN WITH SEMIRIGID CONNECTIONS: I) THEORY
J. DARIO ARISTIZABAL-OCHOA
Profesor Titular Generación 125-Años, Facultad de Minas, Universidad Nacional, Medellín-Colombia, jdaristi@unal.edu.co
Recibido para revisar Mayo 19 de 2009, aceptado Marzo 2 de 2010, versión final Marzo 18 de 2010
RESUMEN: Las matrices de rigidez y de carga de primer y segundo orden de una viga-columna de Timoshenko ortotrópica de sección transversal simétrica con conexiones semirrígidas incluyendo los efectos de la carga axial en los extremos (tracción o compresión) y de las fuerzas cortantes a lo largo del elemento son deducidas de una manera clásica. El modelo de Haringx descrito por Timoshenko y Gere (1961) es adoptado en la formulación de las matrices. Ambas matrices pueden ser utilizadas en los análisis elásticos de estabilidad, de primer y de segundo orden de estructuras aporticadas con elementos viga-columna de Timoshenko de sección transversal simétrica con conexiones rígidas, semirrígidas y simples. Las matrices de rigidez propuestas pueden también ser usadas en el análisis inelástico de pórticos cuyos elementos sufren de degradación por flexión o, en caso contrario, rigidización de las conexiones. Las expresiones cerradas de las matrices de rigidez y de carga desarrolladas y presentadas en este artículo encuentran grandes aplicaciones en los análisis de estabilidad y de segundo orden de estructuras aporticadas compuestas de elementos viga-columna con rigidez a cortante relativamente baja tales como polímeros compuestos ortotrópicos (FRP o “composites”) y elementos cortos elastoméricos de múltiples capas comúnmente usados como aislamiento sísmico en edificios. Los efectos del alabeo torsional a lo largo del elemento no son incluidos.
PALABRAS CLAVE: Pandeo, Columnas; Tipos de construcción; Pórticos; Efectos P-D; Deformaciones por cortante; Análisis de segundo orden; Conexiones semirrígidas; Estabilidad; Pandeo por tracción.
ABSTRACT: The first- and second-order stiffness and load matrices of an orthotropic Timoshenko beam-column of symmetric cross section with semirigid connections including the effects of end axial loads (tension or compression) and shear deformations along the member are derived in a classical manner. Both matrices can be used in the stability, first- and the second-order elastic analyses of framed structures made of Timoshenko beam-columns with rigid, semirigid and simple connections of symmetric cross sections. The “modified” stability approach based on Haringx´s model described by Timoshenko and Gere (1961) is utilized in all matrices. The proposed stiffness matrices can also be used in the inelastic analysis of frames whose members suffer from flexural degradation or, on the contrary, stiffening at their end connections. The closed-form second-order stiffness matrix and load vector derived and presented in this paper find great applications in the stability and second-order analyses of framed structures made of beam-columns with relatively low shear stiffness such as orthotropic composite polymers (FRP or composites) and multilayer elastomeric bearings commonly used in seismic isolation of buildings. The effects of torsional warping along the members are not included. Analytical studies indicate that the buckling load and the stiffness of framed structures are reduced by the shear deformations along the members. In addition, the phenomenon of buckling under axial tension forces in members with relatively low shear stiffness is captured by the proposed equations. Tension buckling must not be ignored in the stability analysis of beam-columns with shear stiffness GAs of the same order of magnitude as EI/h2. The validity of both matrices is verified against available solutions of stability analysis and nonlinear geometric elastic behavior of beam-column structures. Five examples are included that demonstrate the effectiveness of the proposed method and corresponding matrices.
KEYWORDS: Buckling; Columns; Construction Types; Computer applications; Frames; Loads; P-D Effects; Shear deformations; Second-order analysis; Semirigid Connections; Stability; Tension Buckling.
1. INTRODUCCIÓN
En estructuras aporticadas las deflexiones por cortante, los efectos de la componente cortante inducida por la fuerza axial aplicada sobre la deflexión de cada elemento, las deflexiones laterales (efectos P-d) a lo largo de cada elemento, la deriva relativa entre los extremos de cada elemento (efectos P-D), y los efectos de los momentos flectores sobre la rigidez axial causan un comportamiento no lineal con momentos flectores, rotaciones y desplazamientos adicionales. Estos cinco efectos geométricos no lineales no solo alteran la matriz de rigidez de cada elemento y de toda la estructura, sino que también afectan la capacidad de pandeo de cada elemento y de la estructura entera. Por ejemplo, los efectos P-d pueden dar lugar a un pandeo individual del elemento, mientras los efectos P-D pueden dar lugar a inestabilidad estructural o pandeo global de piso. Los efectos combinados de la fuerza axial y de la cortante causan el fenómeno de pandeo a tracción el cual fue observado y reportado por Kelly (2003) en soportes elastoméricos de múltiples capas y discutido por el autor (2005). Estos efectos dependen de: 1) los arriostramientos laterales y las condiciones de soporte del nivel del elemento así como el nivel de toda la estructura; 2) la intensidad y tipo (tracción o compresión) de la carga axial externamente aplicada o inducida a lo largo del elemento; 3) la longitud y dimensiones de la sección transversal o propiedades de cada elemento; y 4) las propiedades de los materiales de cada elemento a lo largo de su longitud y de los ejes principales de su sección transversal.
El comportamiento geométrico no lineal de estructuras aporticadas elásticas compuestas por elementos viga y viga-columna Euler-Bernoulli son generalmente analizados usando dos métodos diferentes: el Método de Elementos Finitos de segundo orden (MEF) y el Método de Funciones Clásicas de Estabilidad (MFCE) descrito por Aristizabal-Ochoa (1997). Sin embargo, el análisis no lineal de segundo orden de estructuras aporticadas compuestas por elementos viga y viga-columna de Timoshenko es más difícil y es usualmente resuelto usando métodos numéricos aproximados.
La matriz de rigidez de segundo orden y el correspondiente vector de carga de un elemento viga-columna prismático sometido a una carga axial constante sobre una fundación elástica uniformemente distribuida (tipo Winkler) a lo largo de toda su longitud con los extremos conectados a apoyos elásticos fueron desarrollados por Areiza, Hurtado y Aristizabal-Ochoa (2005). Los coeficientes de rigidez fueron expresados en términos del coeficiente de balasto de la fundación elástica, la carga axial aplicada, las condiciones de apoyo, la flexión y las deformaciones por cortante. El modelo propuesto por Areiza, Hurtado y Aristizabal-Ochoa (2005) incluye los diferentes modelos de elementos viga y viga-columna disponibles en la literatura técnica incluyendo los basados en las teorías Bernoulli-Euler, Timoshenko, Rayleigh, flexión y cortante. Además, las ecuaciones de transferencia necesarias para determinar las deflexiones laterales, rotaciones, fuerza de cortante, y momento flector a lo largo del elemento. Sin embargo, las soluciones cerradas de las matrices de rigidez y de carga para un elemento viga-columna de Timoshenko con conexiones semirrígidas necesarias para la estabilidad y el análisis elástico de segundo orden de estructuras aporticadas incluyendo los cinco efectos no lineales previamente descritos usando funciones de estabilidad no están disponibles en la literatura técnica.
El objetivo principal de esta publicación es presentar las matrices de rigidez y de carga de primer y de segundo orden de un elemento viga-columna ortotrópica de Timoshenko con conexiones semirrígidas y de sección transversal simétrica utilizando el modelo de Haringx (Timoshenko y Gere 1961, p. 134). Los efectos geométricos no lineales previamente descritos son incluidos en los coeficientes de rigidez axial y transversal y el vector de carga. Sin embargo, estos efectos no se incluyen en la rigidez torsional. Las principales ventajas del método propuesto son: 1) los efectos de las conexiones semirrígidas están condensados en las matrices de rigidez y de carga para carga axial de tracción, compresión y cero sin introducir grados de libertad adicionales; 2) las matrices propuestas capturan el fenómeno de pandeo a tracción; y 3) ambas matrices pueden ser incorporadas en programas de computación sin mayores dificultades. El método y las matrices propuestas sirven para llevar a cabo el análisis de estabilidad elástica, de primer y de segundo orden de estructuras aporticadas hechas de elementos viga-columna ortotrópicos de Timoshenko con conexiones semirrígidas y con sección transversal simétrica. Ambas matrices también pueden ser utilizadas en el análisis inelástico de segundo orden de pórticos cuyos elementos sufren degradación por flexión o rigidización en las conexiones. El modelo propuesto también captura los modelos de elementos viga-columna basados en las teorías de Bernoulli-Euler, Timoshenko, y flexión y cortante. En estructuras aporticadas en las cuales las cargas externas son aplicadas a lo largo de sus elementos, el análisis estático de segundo orden es iterativo requiriendo varios sub-elementos por miembro además de un conjunto de cálculos y chequeos adicionales. Para demostrar la simplicidad y efectividad del método y de las matrices propuestas se presentan cinco ejemplos con detalles en un segundo artículo adjunto.
2. MODELO ESTRUCTURAL
2.1 Descripción del modelo
La figura 1 muestra el elemento viga-columna AB ortotrópica de Timoshenko en tres dimensiones con conexiones semirrígidas. Se supone que está constituido por la viga-columna A´B´ y de las conexiones a flexión 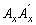 ,
,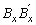 y
y 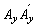 ,
,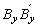 en los extremos A y B alrededor de los ejes locales x y y, respectivamente. Se supone que el elemento A´B es de un material homogéneo, linealmente elástico y ortotrópico con: 1) área total de sección transversal A; áreas efectivas a cortante Asx y Asy (a lo largo de los ejes locales x y y, respectivamente) y los momentos de inercia principales de área Ix e Iy (alrededor de los ejes locales principales x y y, respectivamente), momento de inercia polar del área Je y altura h; 2) las rigideces principales a flexión ExIx, EyIy alrededor de los ejes x y y, respectivamente; 3) rigidez a cortante GxAsx y GyAsy a lo largo de los ejes locales x y y, respectivamente; 4) rigidez torsional GeJe/h; 5) la carga axial P actúa a lo largo del eje centroidal longitudinal z (compresión se supone positiva); y 6) las conexiones a flexión
en los extremos A y B alrededor de los ejes locales x y y, respectivamente. Se supone que el elemento A´B es de un material homogéneo, linealmente elástico y ortotrópico con: 1) área total de sección transversal A; áreas efectivas a cortante Asx y Asy (a lo largo de los ejes locales x y y, respectivamente) y los momentos de inercia principales de área Ix e Iy (alrededor de los ejes locales principales x y y, respectivamente), momento de inercia polar del área Je y altura h; 2) las rigideces principales a flexión ExIx, EyIy alrededor de los ejes x y y, respectivamente; 3) rigidez a cortante GxAsx y GyAsy a lo largo de los ejes locales x y y, respectivamente; 4) rigidez torsional GeJe/h; 5) la carga axial P actúa a lo largo del eje centroidal longitudinal z (compresión se supone positiva); y 6) las conexiones a flexión 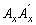 ,
, 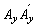 en el extremo A tienen rigideces kax y kay (con dimensiones de momento/radian) sobre los ejes locales x y y, respectivamente. Las relaciones Rax= kax/(ExIx/h) y Ray= kay/(EyIy/h) se denominan índices de rigidez de las conexiones flexibles del extremo A de la columna. Similarmente, las conexiones flexibles
en el extremo A tienen rigideces kax y kay (con dimensiones de momento/radian) sobre los ejes locales x y y, respectivamente. Las relaciones Rax= kax/(ExIx/h) y Ray= kay/(EyIy/h) se denominan índices de rigidez de las conexiones flexibles del extremo A de la columna. Similarmente, las conexiones flexibles 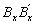 y
y 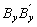 en el extremo B tienen rigideces kbx y kby e índices de rigidez Rbx= kbx/(ExIx/h) y Rby= kby/(EyIy/h).
en el extremo B tienen rigideces kbx y kby e índices de rigidez Rbx= kbx/(ExIx/h) y Rby= kby/(EyIy/h).
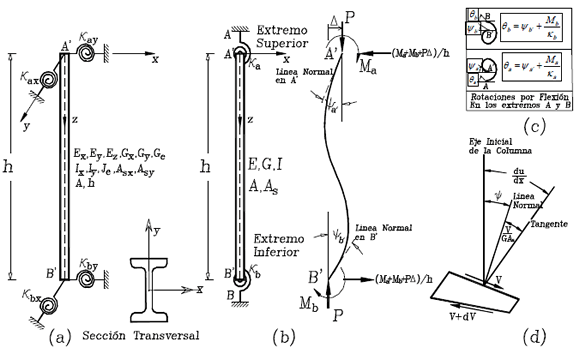
Figura 1. Modelo de columna con deriva parcialmente inhibida y restricciones laterales y rotacionales en los extremos: (a) modelo estructural 3D; (b) rotaciones en los extremos, deriva lateral, momentos y fuerzas en los extremos en el plano de flexión; (c) rotaciones por flexión en los extremos A y B; y (d) elemento diferencial incluyendo flexión y deformaciones por cortante; y d) rotaciones de la sección transversal
Figure 1.Model of column with sidesway partially inhibited and with rotational and lateral end restraints: (a) 3D Structural model; (b) End rotations, lateral sway and end forces and moments in the plane of bending; (c) Bending rotations at ends A and B; and (d) Differential element including bending and shear deformations; and d) Cross section rotations
Los índices de rigidez varían desde cero para una conexión perfectamente articulada a infinito para una conexión perfectamente empotrada. Por conveniencia, los siguientes cuatro parámetros son introducidos:
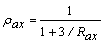 ;
; 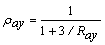 ;
; 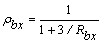 ;
; 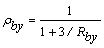 (1a-d)
(1a-d)
Donde rax, ray, rbx, y rby son los factores de fijeza en los extremos A y B de la viga-columna alrededor los ejes centroidales x y y, respectivamente.
2.2 Funciones de estabilidad “modificada” en un plano principal
La matriz de rigidez y el vector de carga de segundo orden de una viga-columna ortotrópica de Timoshenko incluyendo flexión y deformaciones por cortante (figuras 1a-d) en uno de los principales planos de flexión de la sección transversal se formula utilizando el modelo “modificado” propuesto por Haringx y descrito por Timoshenko y Gere (1961, p. 134). Este modelo ha sido utilizado por Aristizabal-Ochoa
(2004 y 2006) en el análisis de estabilidad de columnas y sistemas de multi-columnas 3D y por Kelly (2003) en el análisis de soportes elastoméricos aislados. Las ecuaciones gobernantes en uno de los planos principales de la sección transversal son:
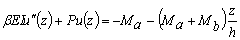 (2a)
(2a)
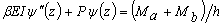 (2b)
(2b)
Donde u(z)= deflexión lateral de la línea central de la viga-columna; y ψ(z)= rotación de la sección transversal como muestra la figura 1c. Las soluciones a las ecuaciones diferenciales (2a) y (2b) son:
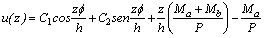 (3a)
(3a)
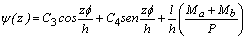 (3b)
(3b)
Donde: 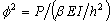
Los coeficientes C1, C2, C3 y C4 se pueden obtener de las siguientes condiciones de frontera:
En A, z= 0: u= 0; ψ= ψa
En B, z= h: u= 0; ψ= ψb
Donde: ψa y ψb= rotaciones de las secciones transversales en los extremos A y B debidas a flexión, respectivamente.
Por lo tanto:
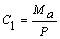 ;
;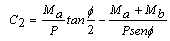
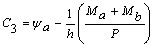 ;
;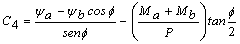
Ya que 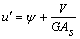 y
y 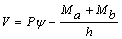 , entonces ψa y ψb son:
, entonces ψa y ψb son:
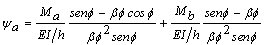 (4a)
(4a)
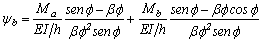 (4b)
(4b)
Donde: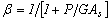 ;
; 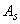 = área efectiva a cortante de la viga-columna; y G= Módulo de cortante en el plano de flexión. Nótese que V incluye la componente Pψ sugerida por Haringx (Timoshenko y Gere 1961, p. 134). Esta componente no fue incluida por Aristizabal-Ochoa (2004) en el análisis de estabilidad de una viga-columna individual. Las ecs. (4a) y (4b) se pueden representar en forma matricial como:
= área efectiva a cortante de la viga-columna; y G= Módulo de cortante en el plano de flexión. Nótese que V incluye la componente Pψ sugerida por Haringx (Timoshenko y Gere 1961, p. 134). Esta componente no fue incluida por Aristizabal-Ochoa (2004) en el análisis de estabilidad de una viga-columna individual. Las ecs. (4a) y (4b) se pueden representar en forma matricial como:
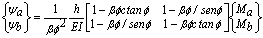 (5)
(5)
Invirtiendo la matriz 2´2 en la ec. (5), 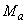 y
y 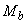 pueden ser expresados en términos de
pueden ser expresados en términos de 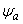 y
y 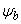 como sigue:
como sigue:
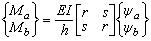 (6)
(6)
Donde r y s son llamadas las funciones de estabilidad “modificada” dadas por las expresiones (7a-b):
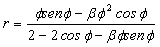 (7a)
(7a) 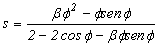 (7b)
(7b)
2.3 Matriz de rigidez a flexión en un plano principal
La matriz de rigidez y el vector de carga 2D del elemento AB desarrollados en este artículo incluyen los efectos de las dos conexiones a flexión AA’ y BB’ (figura 1a) como se explica más adelante.
Los cuatros grados de libertad (GDL) a flexión del elemento AB en uno de los principales planos son mostrados en las figura 1b-c. Nótese que los GDL 1 y 2 corresponden a 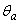 y
y  y los GDL 3 y 4 a
y los GDL 3 y 4 a 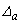 y
y 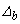 , respectivamente. Los coeficientes de rigidez correspondientes a una rotación unitaria en A son: k11, k21, k31 y k41 (estos son los momentos y fuerzas cortantes en los extremos A y B necesarios para tener una rotación unitaria en A mientras que B permanece totalmente fijo) son obtenidos de la ecuación (6) utilizando las siguientes condiciones en los extremos:
, respectivamente. Los coeficientes de rigidez correspondientes a una rotación unitaria en A son: k11, k21, k31 y k41 (estos son los momentos y fuerzas cortantes en los extremos A y B necesarios para tener una rotación unitaria en A mientras que B permanece totalmente fijo) son obtenidos de la ecuación (6) utilizando las siguientes condiciones en los extremos:
a) En el extremo A: 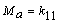 ,
, 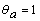 , y
, y 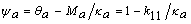
b) En el extremo B: 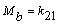 ,
, 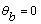 , y
, y 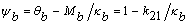
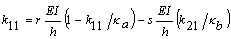 (8a)
(8a)
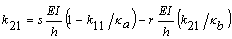 (8b)
(8b)
Ahora, considerando que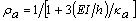 y
y 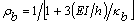 , entonces k11 y k21 se pueden expresar como sigue:
, entonces k11 y k21 se pueden expresar como sigue:
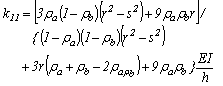 (9)
(9)
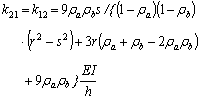 (10)
(10)
Los coeficientes k31 y k41 pueden obtenerse directamente de las condiciones de equilibrio estático:
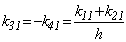 (11)
(11)
El coeficiente k22 correspondiente a  puede ser obtenido simplemente intercambiando
puede ser obtenido simplemente intercambiando 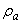 por
por 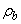 en la ecuación (9) así:
en la ecuación (9) así:
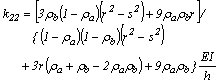 (12)
(12)
El resto de coeficientes de rigidez k32 y k42 correspondientes a  se pueden obtener directamente de las condiciones de equilibrio estático:
se pueden obtener directamente de las condiciones de equilibrio estático:
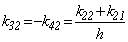 (13)
(13)
Además, los coeficientes de rigidez k33, k44, y k43 correspondientes a las deflexiones laterales 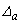 y
y 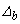 se pueden obtener de las condiciones de equilibrio como sigue:
se pueden obtener de las condiciones de equilibrio como sigue:
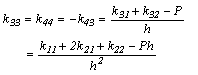 (14)
(14)
En términos del coeficiente de estabilidad 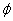 los principales coeficientes de rigidez a flexión son:
los principales coeficientes de rigidez a flexión son:
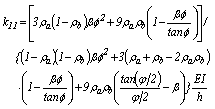 (15)
(15)
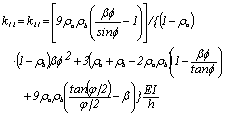 (16)
(16)
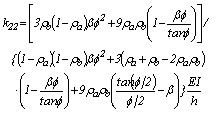 (17)
(17)
Rigideces a flexión de primer orden
Para el caso particular cuando P= 0, las ecuaciones (7a) y (7b) se reducen a 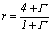 y
y 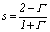 , donde
, donde 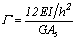 . En consecuencia las expresiones (15), (16) y (17) se reducen a:
. En consecuencia las expresiones (15), (16) y (17) se reducen a:
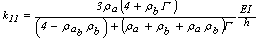 (18)
(18)
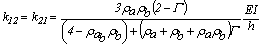 (19)
(19)
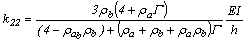 (20)
(20)
Para verificar las ecuaciones (18)-(20), los numeradores y denominadores de las ecuaciones (7a) y (7b) (esto es de las expresiones para r y s, respectivamente) se deben diferenciar cuatro veces de acuerdo con la regla de L’Hospital y luego aplicar el límite P= 0. Las deducciones de las ecuaciones (15)-(20) son presentadas en otra publicación por Aristizabal-Ochoa (2007).
2.4 Rigidez axial (acción como cercha)
La rigidez axial de un elemento viga-columna correspondientes a los GDL axiales 5 y 6 es generalmente k55=k66=-k56 = EA/h. Sin embargo, los momentos flectores en los extremos alre-dedor de cada eje principal afectan este valor produciendo deformaciones axiales adicionales. Ekhande, Selvappalam y Madugula (1989) presentaron un algoritmo basado en la rigidez axial modificada s1EA/h para una viga-columna Bernoulli-Euler, donde s1 es el factor axial de se-gúndo orden. Para una viga-columna de Timo-shenko a flexión biaxial alrededor de los ejes x y y 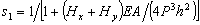 donde Hx y Hy están dadas por las ecuaciones (21) y (22):
donde Hx y Hy están dadas por las ecuaciones (21) y (22):
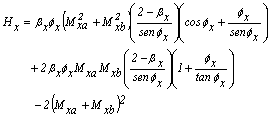 (21)
(21)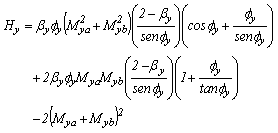 (22)
(22)Mxa, Mxb y Mya, Myb son los momentos flectores en los extremos A y B de la viga-columna en los planos locales xz y yz, respectivamente.Es importante enfatizar que las cargas transversales (distribuidas o concentradas), el desplazamiento relativo de los extremos y los defectos de combadura a lo largo del miembro también afectan la estabilidad y la rigidez axial de las vigas-columna. Aristizabal-Ochoa (1997) discute ampliamente estos efectos en vigas-columnas Bernoulli-Euler de sección transversal doblemente simétrica.
Una vez que la rigidez axial y las de flexión principales (i.e., k11, k21, k22 y k55) son determinadas, la matriz de rigidez 6´6 para una viga-columna 2D (figura 1c) puede ensamblarse utilizando la ecuación (23):
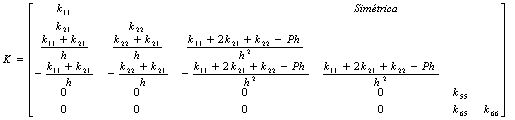 (23)
(23)
El método propuesto y las correspondientes ecuaciones presentadas previamente también son válidos para vigas-columna sujetas a tracción axial. Las ecuaciones (7a), (7b), (15), (16), (17), (21) y (22) son válidas siempre que 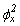 y
y 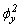 sean positivos (esto es,
sean positivos (esto es,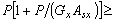 0 y
0 y 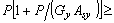 0). Sin embargo, para casos en los cuales
0). Sin embargo, para casos en los cuales 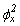 y/o
y/o 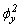 sean negativos (esto es, cargas de tracción ó P<0 y
sean negativos (esto es, cargas de tracción ó P<0 y 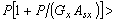 0 y/o
0 y/o 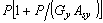 >0), se deben hacer los siguientes tres cambios en las ecuaciones (4)-(7): 1) senf por isenhf; 2) cosf por coshf; 3) tanf por itanhf; y 4) f por if (donde:i =
>0), se deben hacer los siguientes tres cambios en las ecuaciones (4)-(7): 1) senf por isenhf; 2) cosf por coshf; 3) tanf por itanhf; y 4) f por if (donde:i =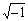 ). Nótese que para el caso P>0 (esto es, carga axial de compresión) y
). Nótese que para el caso P>0 (esto es, carga axial de compresión) y 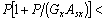 0 y/o
0 y/o 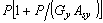 <0 no es factible, dado que este caso requeriría que GxAsx y/o GyAsy fuesen negativos y sus valores absolutos más pequeños que P [ver discusión por Aristizabal-Ochoa (2005) sobre el fenómeno de pandeo a tracción de soportes elastoméricos reportado por Kelly (2003)].
<0 no es factible, dado que este caso requeriría que GxAsx y/o GyAsy fuesen negativos y sus valores absolutos más pequeños que P [ver discusión por Aristizabal-Ochoa (2005) sobre el fenómeno de pandeo a tracción de soportes elastoméricos reportado por Kelly (2003)].
2.5 Rigidez torsional
La interacción de la fuerza axial con la rigidez torsional y el efecto del momento torsor en la rigidez axial y de flexión son despreciados en esta formulación. La rigidez torsional de una viga-columna asumida en este documento corresponde al valor de la torsión pura de Saint Venant (GeJe/h). Si se desea considerar el alabeo por torsión, como por ejemplo en vigas I doblemente simétricas, se requieren dos grados de libertad adicionales consistentes en las rotaciones normales al eje z de ambos extremos de la aleta.
2.6 Momentos fijos en los extremos en un plano principal de flexión
Los momentos fijos en los extremos FEMa y FEMb debidos a cargas transversales al eje z y localizados en uno de los planos principales son:
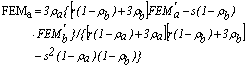 (24a)
(24a)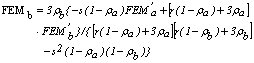 (24b)
(24b)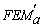 y
y 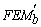 son los momentos fijos cuando los extremos A y B están perfectamente empotrados (i.e., ya= yb= 0).
son los momentos fijos cuando los extremos A y B están perfectamente empotrados (i.e., ya= yb= 0).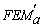 y
y 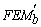 para cuatro casos diferentes de carga mostrados en la figura 2. Las expresiones
para cuatro casos diferentes de carga mostrados en la figura 2. Las expresiones Tabla 1. Expresiones para 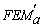 y
y 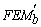 (P= 0)
(P= 0)
Table 1. Expressions for 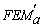 and
and 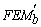 (P= 0)
(P= 0)

Tabla 2. Expresiones para 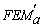 y
y 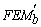 [para
[para 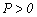 (compresión) o
(compresión) o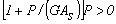 ]*
]*
Table 2. Expressions for 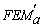 and
and 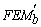 [for
[for 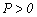 (Compression) or
(Compression) or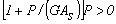 ]*
]*

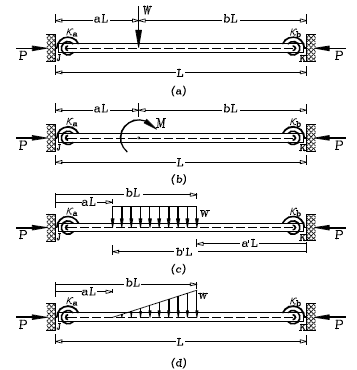
Figura 2. Casos de carga: (a) carga concentrada W; (b) momento concentrado M; (c) carga parcial uniformemente distribuida w; (d) carga parcial linealmente distribuida w
Figure 2. Load cases: (a) Concentrated load W; (b) Concentrated moment M; (c) Uniformly distributed partial load w; (d) Linearly distributed partial load w
4. RESUMEN Y CONCLUSIONES
Las matrices de rigidez de primer y segundo orden y los momentos fijos en los extremos de una viga-columna de Timoshenko ortotrópica con conexiones semirrígidas incluyendo los efectos combinados de flexión más las deformaciones por cortante y la componente de la cortante inducida por la fuerza axial aplicada (Modelo de Haringx) son desarrolladas en una manera clásica. El método propuesto está basado en las funciones de estabilidad “modificadas” para vigas-columna con conexiones semirrígidas (Aristizabal-Ochoa 2004 y 2007). La validez y efectividad de las ecuaciones propuestas son verificadas con soluciones bien documentadas sobre estabilidad elástica de vigas-columna y pórticos planos.
Las principales ventajas del método propuesto incluyen: 1) los efectos de las conexiones semirrígidas son condensados en los coeficientes de la matriz de rigidez y los momentos fijos en los extremos del elemento viga-columna sometido ya sea a tracción, compresión o cero carga axial sin introducir grados de libertad adicionales; 2) las matrices son definidas en términos de las funciones de estabilidad “modificada”; 3) las matrices pueden ser incorporadas en programas de computador sin mayores dificultades haciendo el método práctico y versátil; y 4) el método propuesto es más preciso que cualquier otro método disponible y es capaz de capturar el fenómeno de pandeo bajo fuerzas de tracción axial, el cual es particularmente importante en columnas cortas como soportes elastoméricos laminados comúnmente utilizados para el aislamiento sísmico de edificios.
El método matricial propuesto es quizás el algoritmo más efectivo y práctico para el análisis de segundo orden y de estabilidad elástica de estructuras compuestas de vigas-columna ortotrópicas y prismáticas de sección transversal simétrica con conexiones semirrígidas. El método propuesto también puede ser utilizado en el análisis inelástico de segundo orden de pórticos cuyos elementos sufren degradación por flexión o rigidización en las conexiones. En estructuras aporticadas en las cuales las cargas externas están aplicadas a lo largo de sus elementos, el proceso de determinación de las cargas axiales inducidas en cada elemento en un análisis estático de segundo orden es iterativo, requiriendo más de un conjunto de cálculos y chequeos. Cinco ejemplos se incluyen en un segundo artículo para demostrar la efectividad de las matrices propuestas.
5. AGRADECIMIENTOS
Esta investigación fue llevada a cabo en la Universidad Nacional de Colombia en Medellín. El autor quiere expresar su reconocimiento al Departamento de Ingeniería Civil de la Facultad de Minas y al DIME por el soporte financiero.
6. APÉNDICE
Los siguientes símbolos son utilizados en esta publicación:
As= Área efectiva a cortante de la sección transversal de la viga-columna;
E = Módulo de Young del material;
G = Módulo a cortante del material;
h = Longitud de la viga-columna AB;
I = Momento principal de inercia de la viga-columna alrededor del eje de flexión
L= Luz de la viga;
Ma y Mb= Momentos flectores (antihorarios +) en A y B, respectivamente;
P= Carga axial aplicada en A (+ compresión, -traccion);
Pcr= Carga axial crítica;
Pe= p2EI/h2 = Carga crítica de Euler;
Ra y Rb= Índices de rigidez de las conexiones a flexión en A y B, respectivamente;
u(x)= Deflexión lateral de la línea centroidal de la viga-columna;
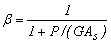 = factor de reducción por cortante;
= factor de reducción por cortante;
D= Deriva del extremo A con respecto al extremo B;
ka y k b = Rigidez a flexión de las conexiones en los extremos A y B, respectivamente;
ra y rb= Factores de fijeza en A y B de la columna AB, respectivamente;
y(x)= Rotación de la sección transversal debido a la flexión pura como muestra la figura 1c;
ya´ y yb´= Rotaciones por flexión de la sección transversal en A´ y B´ con respecto a la línea A´B´, respectivamente;
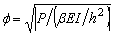 = Función de estabilidad en el plano de flexión;
= Función de estabilidad en el plano de flexión;
qa y qb= Rotaciones de los extremos A y B debido a la flexión con respecto a los ejes verticales, respectivamente. Nótese que:
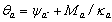 y
y 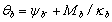 ;
;
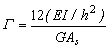 = Coeficiente de cortante para flexión.
= Coeficiente de cortante para flexión.
REFERENCIAS
[1] ARISTIZABAL-OCHOA, J. DARÍO. Large Deflection and Postbuckling Behavior of Timoshenko Beam-Columns with semirigid connections including Shear and Axial Effects, ELSEVIER Journal of Engineering Structures, Vol. 29 (6), June, pp. 991-1003, 2007. [ Links ]
[2] AREIZA-HURTADO, M., VEGA-POSADA, C., AND ARISTIZABAL-OCHOA, J. DARIO. Second-Order Stiffness Matrix and Loading Vector of a Beam-Column with Semirigid Connections on an Elastic Foundation, Journal of Engineering Mechanics, ASCE, 131 (7), pp. 752-762, 2005. [ Links ]
[3] ARISTIZABAL-OCHOA, J. DARÍO. Column Stability and Minimum Lateral Bracing: Effects of Shear Deformations, J. of Engineering Mechanics, ASCE, Vol. 130 (10), Nov., pp. 1223-1232, 2004. [ Links ]
[4] KELLY, J. M. Tension Buckling in multilayer Elastomeric Bearings, J. of Engineering Mechanics, ASCE, Vol. 129 (12), Nov., 2003. pp. 1363-1368. Discussion by ARISTIZABAL-OCHOA, J. DARÍO, Vol. 131 (1), pp. 106-108, 2005. [ Links ]
[5] ARISTIZABAL-OCHOA, J. DARIO. First- and Second-Order Stiffness Matrices and Load Vector of Beam-Columns with Semi-rigid Connections, J. Struct. Engrg., ASCE, 123(5), pp. 669-678, 1997. [ Links ]
[6] BRYANT, R. H. AND BAILE, O. C. Slope Deflection Analysis Including Transverse Shear, J. of the Structural Division, ASCE, Vol. 103, No. 2, Feb., pp. 443-446, 1977. [ Links ]
[7] EKHANDE, S. G., SELVAPPALAM, M., AND MADUGULA, M. K. S. Stability Functions for Three- Dimensional Beam Columns, J. Struct. Engrg., ASCE, 115(2), Feb., pp. 467-479, 1989. [ Links ]
[8] TIMOSHENKO, S. AND GERE, J. Theory of Elastic Stability, 2nd Ed., McGraw-Hill, Chapter II, New York, 1961. [ Links ]














