Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.77 no.164 Medellín Oct./Dec. 2010
IMPLEMENTACIÓN DE UNA NUEVA TÉCNICA DE CONTROL DIGITAL PARA CONVERTIDORES DC-DC Y DC-AC
IMPLEMENTATION OF A NEW DIGITAL CONTROL TECHNIQUE FOR DC-DC AND DC-AC POWER CONVERTERS
FREDY EDIMER HOYOS VELASCO
Universidad Nacional de Colombia, Sede Manizales, fehoyosv@unal.edu.co
FABIOLA ANGULO GARCIA
Universidad Nacional de Colombia Sede Manizales,fangulog@unal.edu.co
JOHN ALEXANDER TABORDA GIRALDO
Universidad del Magdalena, Santa Marta, jtaborda@unimagdalena.edu.co
GERARD OLIVAR TOST
Universidad Nacional de Colombia, Sede Manizales, golivart@unal.edu.co
Recibido para revisar Junio 10 de 2009, aceptado Diciembre 12 de 2009, versión final Enero 28 de 2010
RESUMEN: En este trabajo se presentan resultados experimentales que confirman la validez de una nueva técnica de control digital, por modulación de ancho de pulso (PWM- Digital), para convertidores de potencia DC-DC y DC-AC. El controlador PWM-Digital combina el esquema de control por promedio cero de la dinámica del error (ZAD), ya reportado en la literatura, con el esquema de control por inducción al punto fijo (FPIC) aún en fase de experimentación. El diseño ha sido validado experimentalmente, usando la plataforma digital DSpace, en convertidores DC-DC y DC-AC de baja potencia. Los diagramas de bifurcaciones, calculados numéricamente en la etapa de diseño, concuerdan en un alto porcentaje con los obtenidos en la etapa experimental. Cuando el sistema opera en zona estable se obtiene buen comportamiento a la salida (regulación en el caso DC-DC y rastreo en el caso DC-AC), con bajo error y rechazo a perturbaciones.
PALABRAS CLAVE: Control de convertidores de potencia, convertidores DC-DC, convertidores DC-AC, diagramas de bifurcaciones.
ABSTRACT: In this paper, we show numerical and experimental results obtained when a new PWM-digital control technique is applied to DC-DC and DC-AC converters. The controller combines ZAD (zero average dynamics) and FPIC (Fixed point inducting controller) strategies. The first one has been reported in the literature in the last years and the second one is still in experimental phase. The design has been tested in an experimental way in low power DC-DC and DC-AC converters, using DSpace platform. Numerical and experimental bifurcation diagrams agree. When the system is working in a stable range it has very good performance, showing low error and robustness.
KEY WORDS: Power converter control, DC-DC converters, DC-AC converters, bifurcation diagrams.
1. INTRODUCCIÓN
Un convertidor de potencia es un dispositivo que transforma la energía eléctrica, que toma de la red, en otro tipo de energía eléctrica requerida para una tarea especial. Los convertidores de potencia son de amplia utilización, pues gracias a ellos se puede trabajar con eficiencia, seguridad, fidelidad, confianza y bajo costo [1]. Además, muchas cargas críticas tales como soldadores eléctricos, equipos de telecomunicaciones y aparatos de electromedicina, entre otros, los requieren para su funcionamiento [2]. Los convertidores de potencia deben proporcionar un determinado nivel de tensión, bien sea en tareas de regulación o de seguimiento, y deben ser capaces de rechazar cambios en la carga y en el nivel primario de alimentación. Se estima que el 90% de la energía eléctrica se procesa a través de convertidores de potencia antes de su uso final [3]. Un análisis completo y detallado del funcionamiento y configuración de los diferentes convertidores de potencia se puede encontrar en [2]. Una de las cualidades más apetecidas en estos dispositivos es su eficiencia en el desempeño, la cual puede ser mejorada mediante el uso de dispositivos de conmutación, correctamente implementados, que permitan generar la salida deseada con un bajo consumo de potencia.
El esquema simplificado del convertidor reductor (también llamado convertidor buck o step down), usado en los experimentos, se muestra en la figura 1. Con esta configuración se puede hacer regulación de tensión DC positiva y negativa, y rastreo de señales AC. E es la fuente de alimentación, los dispositivos notados como 1 y 2, actúan como interruptores, L es el inductor, C es el condensador y R es la carga. En general esta carga podría ser del tipo resistiva, no lineal, etc. Sin embargo, las técnicas propuestas han sido probadas para cargas resistivas.
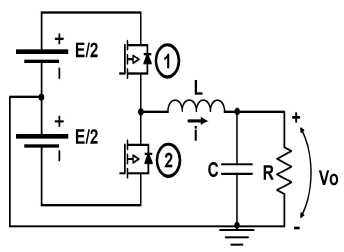
Figura 1. Esquema simplificado del convertidor reductor usado experimentalmente
Figure 1. Simplified diagram of a step down power converter used in experiments
La fuente E proviene de un rectificador de onda completa que está en paralelo con un condensador y es no regulada. Los dispositivos 1, 2 (MOSFETs para nuestro caso) actúan como interruptores que generan un voltaje ±E en los terminales de la carga. Si el diseño experimental fuera sólo para hacer regulación sería posible simplificar el anterior esquema. Sin embargo dado el interés en probar la técnica de control, en tareas de regulación y de seguimiento, se optó por trabajar con este circuito. Así pues, la técnica de control debe determinar el momento de la conmutación de los interruptores. A esta forma de control donde la fuente conmuta entre varios valores se le conoce como modulación por ancho de pulso (PWM por sus siglas en inglés).
A un sistema como el anterior se le denomina sistema de estructura variable, ya que las ecuaciones diferenciales que describen el sistema cambian cuando cambia el estado del interruptor [4]. En general los sistemas de estructura variable presentan dinámicas ricas al realizar variación en sus parámetros. En particular, para el convertidor buck se ha reportado una gran cantidad de estudios de fenómenos no lineales cuando el PWM es generado de manera analógica, es decir, por comparación del error con una señal rampa de referencia (ver por ejemplo [5-9]).
La disminución de costos de plataformas digitales de alto desempeño, ha acelerado el posicionamiento del control PWM-digital, como una solución de diseño viable, ante el tradicional PWM-analógico. Algoritmos de control avanzado, fácilmente programables en dispositivos digitales, pueden ofrecer mejores especificaciones de estabilidad, robustez y frecuencia fija de conmutación. Esta última característica permite filtrar de mejor forma, el ruido de alta frecuencia inherente a los convertidores de potencia [10-11].
La técnica de control ZAD (Zero Average Dynamics), como una solución para garantizar frecuencia fija de conmutación, ha sido estudiada en la literatura [12-18]. En particular, en [14, 15] se presentaron resultados analíticos y numéricos mediante los cuales se demostró que, variando cierto parámetro, el sistema controlado con ZAD presenta inestabilidad por doblamientos de período, seguidos de generación de bandas caóticas y doblamientos de bandas caóticas para finalmente llegar al caos.
De otro lado, en [17-24] se presentó el desarrollo y aplicación de una nueva técnica de control, con la cual se pueden estabilizar, de manera sencilla, órbitas inestables que conviven con el caos. A esta técnica se le ha denominado FPIC (Fixed Point Inducting Control). En particular, en [19] se probó de manera numérica y analítica la capacidad del control FPIC para estabilizar la órbita inestable de período uno que convive con el caos, en el sistema controlado con ZAD. Sin embargo, hasta la fecha, no existen resultados experimentales que permitan mostrar la aplicabilidad del método.
En este trabajo se presentan resultados experimentales del uso de los controladores ZAD-FPIC actuando en conjunto, tal como se sugirió en [17]. Se ha incluido la medición del voltaje de alimentación, con el objeto de mejorar el desempeño del controlador. En la sección 2 se describe el modelo matemático del sistema, se exponen las estrategias ZAD y FPIC y se hace un breve resumen de su comportamiento. En la sección 3 se explica el diseño electrónico del sistema. En la sección 4 se presentan los resultados experimentales y se comparan los diagramas de bifurcaciones numéricos y experimentales. Finalmente, en la sección 5, se presentan las conclusiones y el trabajo futuro.
2. CONSIDERACIONES MATEMÁTICAS
En esta sección se presentan las herramientas generales necesarias para analizar y controlar el convertidor de potencia.
2.1 Modelo del sistema
De la figura 1 se obtienen las ecuaciones diferenciales que describen el sistema:
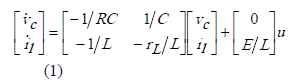
Las variables de estado son el voltaje en el condensador (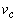 ) y la corriente en el inductor (
) y la corriente en el inductor (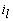 ). rL es la resistencia interna del inductor. u es la señal de control y toma valores en el conjunto discreto {-1,1} indicando la posición de los interruptores. E es la fuente que alimenta al convertidor y R, L y C son los elementos constitutivos del circuito, tal como se dijo anteriormente. Esta ecuación puede ser notada de manera compacta como
). rL es la resistencia interna del inductor. u es la señal de control y toma valores en el conjunto discreto {-1,1} indicando la posición de los interruptores. E es la fuente que alimenta al convertidor y R, L y C son los elementos constitutivos del circuito, tal como se dijo anteriormente. Esta ecuación puede ser notada de manera compacta como 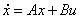 , con x1=vc y x2=iL. Cuando la señal de control cambia, las ecuaciones diferenciales cambian instantáneamente (sistema de estructura variable). El esquema de control que se usará en este trabajo corresponde con una modulación por ancho de pulso al centro, es decir, en el primer y en el último tramo del período, la posición del interruptor será la misma. En particular el sistema operará de la siguiente manera:
, con x1=vc y x2=iL. Cuando la señal de control cambia, las ecuaciones diferenciales cambian instantáneamente (sistema de estructura variable). El esquema de control que se usará en este trabajo corresponde con una modulación por ancho de pulso al centro, es decir, en el primer y en el último tramo del período, la posición del interruptor será la misma. En particular el sistema operará de la siguiente manera:
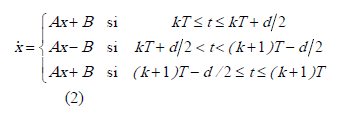
T es el período de conmutación. A d se le conoce como el "ciclo de trabajo" y de manera normalizada se obtiene de dividir el tiempo en que la fuente está en +E entre el período de conmutación. El diseño de un controlador por modulación de ancho de pulso consiste en generar una estrategia, por medio de la cual, se genere el ciclo de trabajo, de tal manera que el sistema opere como se desea. En este artículo se usa la técnica de promedio cero en la dinámica del error (ZAD), la cual se describe a continuación y se basa en el hecho de que al ser un sistema de estructura variable se le pueden aplicar los principios del control en modos deslizantes, de tal manera que la dinámica del error sea cero en promedio, en cada iteración.
2.2 Técnica ZAD
Sea la función s(x) definida como:
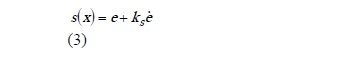
Con 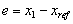 el error de la salida, donde xref corresponde al voltaje de referencia. De este modo s(x) (notada en este documento, de manera indistinta como s(x(t)) o s) define una dinámica de primer orden en la variable error e. El objetivo de la estrategia de control es hacer que, en promedio, en cada iteración (o período de muestreo), la dinámica definida por (3) tenga valor cero, es decir:
el error de la salida, donde xref corresponde al voltaje de referencia. De este modo s(x) (notada en este documento, de manera indistinta como s(x(t)) o s) define una dinámica de primer orden en la variable error e. El objetivo de la estrategia de control es hacer que, en promedio, en cada iteración (o período de muestreo), la dinámica definida por (3) tenga valor cero, es decir:
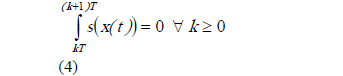
Resolver esta ecuación implica resolver una ecuación trascendente al inicio de cada ciclo, lo que retarda la acción de control. En [23] se demostró analíticamente, para el sistema de ecuaciones diferenciales descrito por (1) con la ley de control dada por (3), que el error en estado estacionario es inferior al 0.2%. Sin embargo, dado los problemas computacionales asociados, en [17] se mostró que una buena alternativa es suponer que la superficie s(x) se comporta como una recta a tramos, lo cual fue validado posteriormente en [23]. Así pues suponiendo a s(x) como una recta a tramos, la ecuación (4) es fácil de resolver y se obtiene el ciclo de trabajo como [17]:
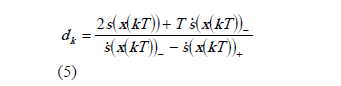
donde 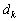 es el ciclo de trabajo a ejecutar en el tiempo entre kT y (k+1)T,
es el ciclo de trabajo a ejecutar en el tiempo entre kT y (k+1)T, 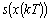 es el valor de la función s al inicio del ciclo,
es el valor de la función s al inicio del ciclo, 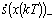 es el valor de la derivada de la función cuando se hace
es el valor de la derivada de la función cuando se hace 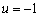 y
y 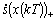 es el valor de la derivada de la función cuando se hace u=+1. Existen dos problemas principales asociados a esta técnica.
es el valor de la derivada de la función cuando se hace u=+1. Existen dos problemas principales asociados a esta técnica.
El primero es que se requieren los valores de los estados al inicio de cada período, ya que la función s y sus derivadas dependen de los estados. El segundo es que se necesitan los valores de los parámetros R, L y C. El primer problema sólo es representativo en la variable corriente y se resuelve haciendo uso del hecho de que, siendo el sistema de pulso al centro y teniendo en cuenta las consideraciones sobre s, el valor de la variable al momento de muestrear corresponde con su valor medio. Así pues, se toman varias muestras, igualmente espaciadas en el tiempo y simétricas respecto de la mitad del ciclo, y se obtiene su promedio. El segundo problema se ha resuelto, en este primer prototipo, estimando la carga por medición de la corriente.
Es importante hacer las siguientes anotaciones:
1. Al disponer del ciclo de trabajo al inicio de cada período, es posible obtener la solución analítica de las ecuaciones diferenciales dadas por (1), es decir, se puede construir un mapa estroboscópico del sistema. Esto ha permitido hacer un amplio estudio de su comportamiento, tanto de manera numérica como analítica [14-23].
2. Siendo coherentes con (2) y con (4), en (5) el ciclo de trabajo no se ha normalizado a 1, sin embargo, en las gráficas donde aparece el ciclo de trabajo, por facilidad de visualización, éste se ha normalizado a 1 (d/T).
3. Cuando se use la estrategia ZAD como único controlador en el sistema, entonces al ciclo de trabajo calculado de (5) se le debe aplicar la función saturación. Así pues, si al aplicar la ecuación (5) resultara un valor superior a T o inferior a 0, estos valores deben ser saturados a T y 0 respectivamente y en el siguiente ciclo, con los nuevos datos, calcular nuevamente la ley de control. Sin embargo, cuando el ZAD opera con FPIC, se debe aplicar la función saturación al ciclo de trabajo generado después de conjuntar ambas técnicas, como se describe más adelante. Además de la conmutación de la fuente, la saturación del ciclo de trabajo es uno de los principales generadores de fenómenos no lineales ya reportados en este sistema.
2.3 Técnica de control FPIC
Esta técnica de control, llamada control por inducción al punto fijo, fue presentada primero en [17], luego probada numéricamente en [18-22] y más recientemente en [24]. Sin embargo resultados experimentales que mostraran su efectividad aún no han sido reportados.
Teorema de FPIC
Sea un sistema descrito por un conjunto de ecuaciones en diferencias:
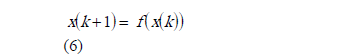
donde 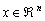 y
y 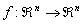 . Supóngase que existe un punto fijo x*, el cual es inestable y que se corresponde con la órbita que se quiere controlar, es decir
. Supóngase que existe un punto fijo x*, el cual es inestable y que se corresponde con la órbita que se quiere controlar, es decir 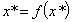 . Sea
. Sea 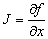 el jacobiano del sistema, entonces dado que el sistema es inestable, existe al menos un i, tal que
el jacobiano del sistema, entonces dado que el sistema es inestable, existe al menos un i, tal que 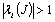 , donde
, donde 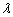 corresponde a los valores propios del sistema. Bajo estas condiciones, la ecuación
corresponde a los valores propios del sistema. Bajo estas condiciones, la ecuación
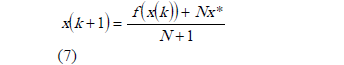
garantiza estabilización del punto fijo para algún N real positivo.
Demostración
Inicialmente debe notarse que en la ecuación (7) el punto fijo no se ha alterado. En este caso el Jacobiano del nuevo sistema puede ser expresado como:
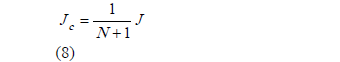
donde Jc es el Jacobiano del sistema controlado y J es el Jacobiano del sistema inestable. Por lo tanto una correcta asignación de N garantiza estabilización del equilibrio, ya que los valores propios del sistema controlado serán los valores propios del sistema original divididos entre el factor N + 1. Una manera directa de calcular N es a través del criterio de Jury. Teniendo en cuenta las estrategias ZAD y FPIC, se procede a calcular el nuevo ciclo de trabajo como:
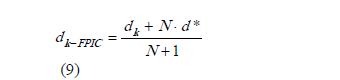
Donde dk se calcula de (5) y d* se calcula, al inicio de cada período, de la siguiente manera (para conmutación entre +E y -E)
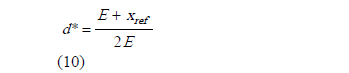
Esta forma de calcular el valor del ciclo de trabajo en cada iteración, incluyendo el valor de la fuente de alimentación, hace que el sistema se vuelva un control adaptativo ya que actualiza constantemente su valor dependiendo de la variación en la fuente y así ejerce un mejor control sobre el sistema. Así pues la ecuación (9) incorpora las técnicas ZAD y FPIC, y tal como se dijo, a esta ecuación se le debe aplicar la función saturación definida anteriormente. Una descripción completa de los procedimientos presentados en la sección 2 puede ser encontrada en [17, 24].
3. CONSIDERACIONES DE HARDWARE
El prototipo desarrollado consta de dos partes principales que están relacionadas con el hardware y con el software. La primera está compuesta por la tarjeta inversora, el filtro LC y la parte de adecuación y medición de señales. La segunda, correspondiente a la parte digital, está desarrollada en la tarjeta de control y desarrollo DS1104, donde se implementan las técnicas de control ZAD y FPIC. Esta tarjeta se programó desde la plataforma simulink de MatLab® y cuenta con una interfaz de visualización llamada ControlDesk. Los controladores son implementados en simulink y son descargados al DSP para trabajar a una frecuencia dada.
Para la implementación de las técnicas de control ZAD y FPIC es necesario conocer algunos valores de parámetros tales como: L, C, rL, Fs (Frecuencia de muestreo de corriente), Fc (Frecuencia de conmutación de los interruptores dada por 1/T), ks y N. Estos valores se consideran fijos. Además de estos datos, se deben conocer, al inicio de cada período, los valores de las variables de estado del sistema: vc e il, y los valores de E y R. Estos dos últimos datos se requieren con el objetivo de hacer robusto el sistema ante cambios de la señal de entrada y de la carga. Sin embargo, dado que la carga puede variar, ésta se estima usando la ley de Ohm, por lo cual requiere medirse también la corriente en la carga (iR). Para la medición de corriente en la carga se usó una resistencia shunt y para la medición de voltaje en el condensador se usó un divisor de tensión.
Para ejecutar las técnicas de control es necesario tener la señal de referencia y sus derivadas. Con base en esto, se programó en simulink un bloque de tal manera que cuando éste es compilado en la DSP, se puede cambiar manualmente su amplitud y frecuencia. Finalmente, y antes de proceder a controlar el sistema, se configuran las señales del PWM a una frecuencia de 5 kHz (frecuencia de conmutación) para cerrar el lazo de control. La frecuencia de muestreo es, sin embargo, de 25 kHz, con el objeto de obtener el valor medio de la corriente, lo cual se ha hecho de la siguiente manera: cada 5kHz se toma una muestra de corriente, al final se suman las muestras y se divide entre cinco. Debe tenerse en cuenta que cada dato de corriente y voltaje tienen un ruido asociado. Por facilidad, para el manejo de datos y visualización gráfica, se ha normalizado el valor de la constante ks asociada a la función s, de tal manera que esta última se obtiene como 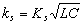 , donde Ks es el valor presentado en las gráficas.
, donde Ks es el valor presentado en las gráficas.
4. RESULTADOS
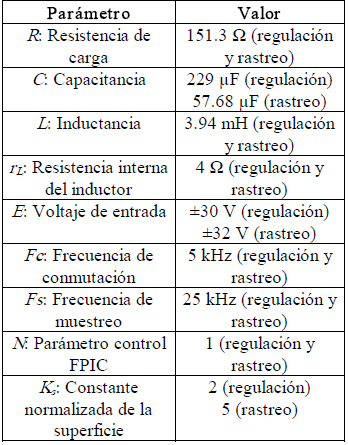
Los resultados que se presentan a continuación fueron obtenidos con el prototipo experimental y con los parámetros definidos en la tabla 1.
Tabla 1. Datos del prototipo experimental
Table 1. Data of experimental prototype
De manera general puede decirse que un diagrama de bifurcaciones muestra el comportamiento de un sistema, en estado estacionario, en la medida que se varía un parámetro. En este artículo se varían el parámetro Ks, la resistencia de carga y el valor de la fuente de alimentación E. Inicialmente se muestran tres diagramas de bifurcaciones variando Ks: el primero (figura 2(a)) corresponde al ciclo de trabajo obtenido por simulación usando como control la estrategia ZAD sola, suponiendo además que se mide la corriente de la misma manera que en el prototipo experimental, e incluyendo en las medidas un ruido seudo-aleatorio de distribución uniforme y de valor máximo 0.04. Se observa que el sistema es inestable para todo Ks. Esto probablemente es debido a la alta sensibilidad del ZAD al cálculo del ciclo de trabajo, el cual con el ruido simulado, torna el sistema inestable. Con el objeto de comparar los diagramas de bifurcaciones numérico y experimental, en la figura 2(b) se muestra el comportamiento de la variable voltaje del sistema simulado con ZAD y FPIC con las mismas consideraciones del caso anterior. Aunque no se presenta el ciclo de trabajo, este varía entre 0.8 y 0.86, aproximadamente, para Ks>1.2. La figura 2(c) muestra el diagrama de bifurcaciones experimental. En ella se observa que el sistema tiene un rango de operación estable para aproximadamente Ks > 1.15. Aunque el diagrama numérico muestra órbitas de alto período no es posible distinguir éstas en el diagrama experimental debido a errores de muestreo, retardos de tiempo, resolución de los convertidores A/D-D/A, etc. Sin embargo, la característica más importante, que es aquella relacionada con la estabilidad, es bastante coincidente en la parte experimental y en la numérica.
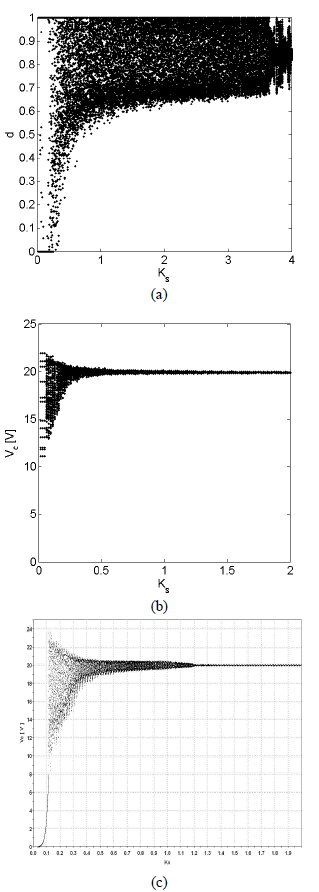
Figura 2. Diagramas de bifurcaciones: (a) Numérico ZAD, (b) Numérico ZAD+FPIC (c) Experimental
Figure 2. Bifurcation diagrams: (a) Numerical results with ZAD, (b) Numerical results with ZAD+FPIC, (c) Experimental results
El error de regulación cuando el sistema trabaja en zona estable es menor a 0.5% y para valores de Ks < 1.15 el sistema va perdiendo, lentamente, su capacidad de regular a través de un comportamiento caótico, en el cual el ciclo de trabajo cada vez se separa más del valor de estado estable (0.833), provocando a su vez mayor error.
Nótese que para valores de Ks > 0.15, en general los dos diagramas son coincidentes. Para valores por debajo de 0.15, el método numérico no tiene restricciones y sigue calculando el valor correspondiente. Sin embargo, el sistema físico maneja restricciones, y con este valor se aísla la fuente.
En la figura 3 se muestra de manera experimental, el comportamiento del sistema en estado estacionario para un valor de referencia de 20V, Ks = 2 y N=1. El ciclo de trabajo está cerca a 0.85 y el voltaje a la salida permanece cerca a los 20 V con un error inferior al 0.5%.
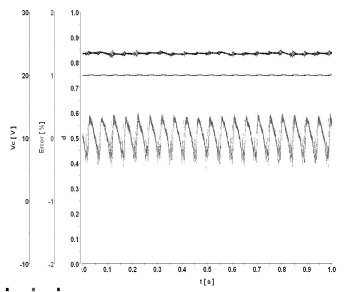
Figura 3. Comportamiento del sistema en estado estacionario para Ks = 2. Resultados experimentales
Figure 3. Steady state behavior for Ks = 2. Experimental results
En la figura 4 se presentan los diagramas de bifurcaciones experimentales, cuando se usan como parámetros de bifurcación: la resistencia R en 4(a) y el voltaje de alimentación E en 4(b). Para el caso (a) E =20V, Ks = 2 y la carga resistiva es variada entre 150Ω y 340Ω. Para el caso (b) R =151.3Ω, Ks = 2 y la fuente es variada entre 21V y 33V. En 4(a) se observa que el sistema presenta buena regulación en todo el rango de variación de la carga y en 4(b) se prueba la robustez del sistema ante cambios en la fuente de voltaje. De 4(b) se observa que el sistema continúa regulando, gracias a que, en cada período, el controlador actualiza su valor. El error fue inferior al 1% en ambos casos lo que muestra buena capacidad del sistema para manejar cambios en la fuente de alimentación y en el valor de la carga.
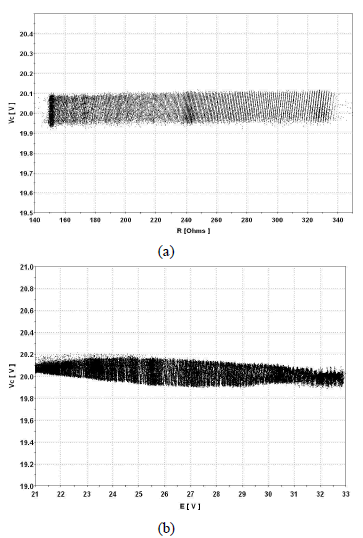
Figura 4. Diagramas de bifurcaciones experimentales: (a) Variando la carga R, (b) Variando la fuente E
Figure 4. Experimental bifurcation diagrams: (a) R is the bifurcation parameter (b) E is the bifurcation parameter
En la figura 5 se presentan los resultados de usar el prototipo experimental en tareas de rastreo. En 5(a) la referencia es una onda definida por xref=20sen(40pt). En particular se presentan las siguientes variables: el voltaje de salida (vc), el ciclo de trabajo normalizado a 1 y el error, en porcentaje, calculado respecto de la amplitud. El error máximo es del 5%.
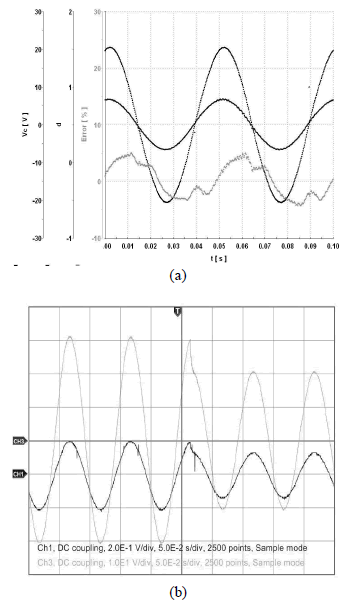
Figura 5. Comportamiento del sistema: (a) 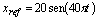 , (b) Ante cambios en la amplitud
, (b) Ante cambios en la amplitud
Figure 5. Behaviour of the system (a) 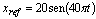 , (b) When there is a change in the amplitude
, (b) When there is a change in the amplitude
El error ha aumentado respecto al caso de regulación, dado que al aumentar la frecuencia de la señal de referencia, ésta crece entre un período y el siguiente. Es de esperarse que a mayor frecuencia de la señal de referencia haya mayor error en la salida. Este problema se puede solucionar disminuyendo el tiempo de conmutación (T). En la figura 5(b) se presenta el comportamiento del sistema cuando hay un cambio en la referencia, pasando de amplitud 30V a 20V. Las variables de estado mostradas son el voltaje en el condensador y la corriente en la carga.
5. CONCLUSIONES Y TRABAJO FUTURO
Con este trabajo se ha avanzado significativamente en el área de implementación práctica de las técnicas FPIC y ZAD, cuyas ventajas ya han sido probadas analítica y numéricamente. El error en regulación fue mucho menor que el error en seguimiento. El primero tuvo un error inferior al 1%, mientras que el segundo tuvo un error inferior al 5%. Este problema puede ser resuelto disminuyendo el tiempo de conmutación.
Los diagramas de bifurcaciones obtenidos por simulación (numérico) y experimental han mostrado buena coincidencia. Sin embargo debido a problemas como retrasos propios de hardware y software, resolución de los convertidores, errores de medida y ruido, entre otros, no es posible obtener todos los detalles de los comportamientos dinámicos esperables. Dado que cuando un sistema presenta dinámicas ricas, generalmente coexisten varios tipos de soluciones, los problemas anteriormente mencionados hacen que éste caiga en diferentes cuencas de atracción y posiblemente no exhiba el comportamiento esperado. Sin embargo es alentador observar la alta coherencia entre ambos diagramas de bifurcaciones.
La técnica ZAD, como única técnica de control aplicada al convertidor [16], no muestra tan buen desempeño como cuando trabaja conjuntamente con el controlador FPIC. Esto se puede apreciar comparando el diagrama numérico de la figura 2(a) y el diagrama experimental de la figura 2(c). Es importante anotar que resultados experimentales de este controlador no habían sido reportados. Aún más, al medir el valor de la fuente de voltaje en cada iteración, y adicionar este valor al controlador, se logró que el sistema se volviera estable aún ante variaciones en la fuente de voltaje.
Se observó que el prototipo propuesto tiene buena regulación ante cambios en la fuente de alimentación y ante variaciones en la carga. Con el diseño propuesto también se ha ensayado el seguimiento de señales periódicas de tipo cuadrada, triangular, rampa y sinusoidal, de frecuencia y amplitud variables y su respuesta ha sido satisfactoria.
Se ha demostrado experimentalmente que la técnica de control propuesta, FPIC, es fácil de calcular (sólo requiere conocimiento del estado estacionario del sistema), fácil de aplicar (se basa en un promedio) y ayuda a estabilizar el sistema.
Actualmente se trabaja en otro prototipo con el cual se disminuyan las pérdidas en la bobina, se aumente la potencia del convertidor y la velocidad de muestreo, se puedan agregar otro tipo de cargas y además use sistemas autónomos para el procesamiento de la señal y generación de la acción de control. Este nuevo prototipo ampliará el campo de aplicación de la técnica ZAD+FPIC.
REFERENCIAS
[1] HART D. Electrónica de Potencia. Prentice Hall, Madrid, España, 2001. [ Links ]
[2] MOHAN N., UNDELAND T. AND ROBBINS W. Power Electronics: Converters, Applications and Design, J. Wiley 1995. [ Links ]
[3] BANERJEE S. AND VERGHESE G.C., Eds. Nonlinear Phenomena in Power Electronics. IEEE Press, Piscataway, 2001.
[4] UTKIN V. I. Variable structure systems with sliding modes. IEEE Transactions on Automatic Control, vol. 22. pp. 212-222. 1977. [ Links ]
[5] BANERJEE S., OTT E., YORKE J.A. AND YUAN G.H. Anomalous bifurcations in dc-dc converters: Borderline collisions in piecewise smooth maps. In Proceedings IEEE Power Electronics Specialists Conference. pp 1337-1344. 1997. [ Links ]
[6] FOSSAS E. AND OLIVAR G. Study of chaos in the buck converter. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, vol. 43, No. 1, pp 13-25. 1996. [ Links ]
[7] HAMILL D.C, DEANE J.H.B. AND JEFFERIES D.J. Modeling of chaotic DC-DC converters by iterated nonlinear mappings. IEEE Transactions on Power Electronics, vol. 7, No. 1. pp 25-36. 1992. [ Links ]
[8] OLIVAR, G. Chaos in the Buck Converter. PhD thesis, Universidad Politécnica de Cataluña, Spain. 1997. Disponible en: http://www.tesisenxarxa.net/TDX-0921104-170716/index_an.html [ Links ]
[9] EL AROUDI, A., DEBBAT, M., GIRAL, R., OLIVAR, G., BENADERO, L., AND TORIBIO, E. Bifurcations in dc-dc switching converters: review of methods and applications. International Journal of Bifurcation and Chaos, vol 15, No. 5, pp. 1549 - 1578. 2005. [ Links ]
[10] LIU, Y.F. AND SEN, P.C. Digital control of switching power converters. Proceedings of 2005 IEEE Conference on Control Applications, CCA, Toronto, pp. 635-640. 2005. [ Links ]
[11] SYED, A., AHMED, E. AND MAKSIMOVIC D. Digital PWM Controller with Feed-Forward Compensation. Proc. IEEE Appl. Power Electron. Conf., pp.60-66. 2004. [ Links ]
[12] FOSSAS E., GRIÑÓ R., AND BIEL D. Quasi-sliding control based on pulse width modulation, zero average and the L2 norm, in Advances in Variable Structure System, Analysis, Integration and Applications. Ed. by Xinghuo Yu and Jian-Xin Xu. Ed. World Scientific.. pp 335-344. 2001. [ Links ]
[13] RAMOS, R., BIEL, D., FOSSAS, E. AND GUINJOAN, F. A Fixed-frequency quasi-sliding control algorithm: Application to power inverters design by means of FPGA implementation. IEEE Transactions on Power Electronics, Vol. 18, No. 1, pp. 344-355. 2003. [ Links ]
[14] ANGULO, F., OLIVAR, G., AND TABORDA, A. Continuation of periodic orbits in a ZAD-strategy controlled buck converter. Chaos, Solitons and Fractals, Vol. 38, pp. 348 - 363. 2008. [ Links ]
[15] ANGULO, F., FOSSAS, E., AND OLIVAR, G. Transition from periodicity to chaos in a PWM controlled buck converter with ZAD strategy. Int. Journal of Bifurcations and Chaos, Vol. 15, No. 10 pp. 3245 - 3264. 2005. [ Links ]
[16] ANGULO, F., OCAMPO, C., OLIVAR, G., AND RAMOS, R. Nonlinear and nonsmooth dynamics in a DC - DC buck converter: two experimental set-ups. Nonlinear Dynamics, Vol. 46, pp. 239 - 257. 2006. [ Links ]
[17] ANGULO, F. Análisis de la dinámica de convertidores electrónicos de potencia usando PWM basado en promediado cero de la dinámica del error (ZAD). Tesis de doctorado. Universidad Politécnica de Cataluña, 2004. Disponible en: http://www.tdx.cesca.es/TDX-0727104-095928/ [ Links ]
[18] TABORDA, J. Análisis de bifurcaciones en sistemas de segundo orden usando PWM y promediado cero de la dinámica del error. Tesis de maestría. Universidad Nacional de Colombia - Sede Manizales. 2006. [ Links ]
[19] ANGULO, F., FOSSAS E., OCAMPO C. AND OLIVAR G. Stabilization of chaos with FPIC: application to ZAD strategy buck converters. In Proceedings: 16th World Congress International Federation of Automatic Control. Praga (República Checa), July 4 - 8. 2005. [ Links ]
[20] BIEL D., CARDONER R. AND FOSSAS E. Tracking signal in a centered pulse ZAD power inverter. In Proceedings: International Workshop on Variable Structure Systems, Alghero, ( Italy ), June 5-7. 2006 [ Links ]
[21] ANGULO, F., BURGOS J.E. AND OLIVAR G. Chaos stabilization with TDAS and FPIC in a buck converter controlled by lateral PWM and ZAD. In Proceedings: Mediterranean Conference on Control and Automation, July 27 - 29, Athens, Greece . 2007. [ Links ]
[22] ANGULO F., OLIVAR G., TABORDA A. AND HOYOS F. Non-smooth dynamics and FPIC chaos control in a DC/DC ZAD strategy power converter. In proceedings: EUROMECH nonlinear Dynamics conference, Saint Petersburg ( Russia ), June 30-July 4, 2008. [ Links ]
[23] ANGULO F., FOSSAS E., TERE M-SEARA AND OLIVAR G. Bounding the output error in a buck power converter using perturbation theory. Hindawi Publishing Corporation Mathematical Problems in Engineering, Vol. 2008, Article ID 732039, 20 pages doi:10.1155/2008/7320. 2008. [ Links ]
[24] TABORDA A., SANTINI S., DI BERNARDO M. AND ANGULO F. Active Chaos Control of a Cam-Follower Impacting System using FPIC Technique. Chaos09, London ( UK ) June 22 - 24, 2009. [ Links ]














