Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.77 no.164 Medellín Oct./Dec. 2010
MODELO MATEMÁTICO PARA EL PROCESO TÉRMICO DE PRODUCTOS CÁRNICOS DE GEOMETRÍA CILÍNDRICA
MATHEMATICAL MODELLING FOR THE THERMAL PROCESS OF CYLINDRICAL MEAT PRODUCTS
DIANA ARBOLEDA
Joven Innovador. Centro de Investigación y Desarrollo Cárnico, dianarboleda@gmail.com
VÍCTOR VALENCIA
Jefe de Investigación. Centro de Investigación y Desarrollo Cárnico, victor@zenu.com.co
JAIRO ESPINOSA
Director GAUNAL. Universidad Nacional de Colombia sede Medellín, jespinov@unal.edu.co
OSCAR OCHOA
Director. Centro de Investigación y Desarrollo Cárnico, oaochoa@zenu.com.co
Recibido para revisar Marzo 20 de 2009, aceptado Diciembre 18 de 2009, versión final Marzo 1 de 2010
RESUMEN: El objetivo del trabajo fue desarrollar un modelo matemático que permita simular el comportamiento de la temperatura y la pérdida de peso en un producto cárnico con forma cilíndrica durante el proceso térmico. Para desarrollar el modelo se utilizó una forma geométrica similar a la del producto real la cual se dividió en volúmenes de control representados por cilindros concéntricos. Sobre este volumen de control se realizó un balance de masa y energía y se obtuvo el modelo propuesto en este trabajo, el cual fue validado con datos obtenidos de pruebas experimentales. Se obtuvo un modelo matemático que representa de manera precisa el comportamiento de la temperatura en varias posiciones a lo largo del radio del producto, sin embargo el modelo de pérdida de peso no exhibe la misma calidad debido a limitaciones en los instrumentos de medición. Los modelos se simularon en MATLAB ® utilizando la herramienta Simulink
PALABRAS CLAVE: proceso térmico, producto cárnico, modelamiento matemático.
ABSTRACT: The objective of this work was to develop a mathematical model to simulate the behavior of temperature and weight losses in a cylindrical meat product during the thermal process. A geometric shape similar to the real product was used to develop the model. Such shape was divided in concentric cylinders. Along the concentric cylinders a mass and energy balance was developed. This model was validated with experimental data. The mathematical model represents properly the behavior of temperature at various locations along the radius of the product; however the precision of the weight losses was not of such a high quality due to instrumental limitations. The models were simulated in MATLAB Simulink ®
KEY WORDS: Thermal process, meat product, mathematical modelling.
1. INTRODUCCIÓN
Las técnicas de procesamiento térmico son ampliamente utilizadas para mejorar la calidad y la seguridad de los alimentos y a su vez extender la vida útil de los mismos [1]. En general, el proceso térmico al que son sometidos los alimentos se compone de dos operaciones principales: el calentamiento y el enfriamiento. El calentamiento, posee funciones importantes entre las que se encuentran: el desarrollo de sabor y la estructura del alimento [2]. Por otra parte, el enfriamiento reduce la velocidad de deterioro químico y enzimático e inhibe el crecimiento microbiano extendiendo la vida útil. [3]
Los procesos térmicos tienen como principio el intercambio de masa y calor entre el alimento y el medio de procesamiento. Es necesario conocer los mecanismos de transferencia de calor y de masa presentes para el diseño de procesos térmicos más económicos y eficientes que mejoren la calidad y la seguridad del alimento. Cuando el mecanismo de un proceso es bien comprendido, se pueden desarrollar modelos matemáticos que lo representen. [1]
Es de gran importancia contar con un diseño correcto del proceso térmico, ya que esto permite controlar las pérdidas de humedad, definir las características organolépticas deseadas, garantizar la seguridad del producto y tener un proceso con un rendimiento adecuado para la comercialización del mismo [4]. El proceso de calentamiento le imprime al producto atributos especiales como mejor sabor, palatabilidad, textura, extensión de la durabilidad y modificaciones del color [5].
Contar con un modelo matemático que simule el comportamiento de la temperatura del producto y su pérdida de humedad permite diseñar procesos óptimos que garanticen todas las condiciones que debe tener el producto y que son exigidas por el consumidor. El objetivo de este trabajo es medir y analizar la temperatura y el contenido de humedad durante el proceso térmico al cual son sometidos los productos cárnicos emulsificados de geometría cilíndrica y proponer un modelo matemático que lo represente.
2. MATERIALES Y MÉTODOS
2.1 Análisis experimental
2.1.1 Muestra utilizada
La muestra bajo estudio es un producto cárnico emulsificado de geometría cilíndrica embutido en tripa fibrosa permeable a la humedad. El producto tiene como dimensiones 16 cm de diámetro y 80 cm de longitud.
2.1.2 Tratamiento térmico
El tratamiento térmico consta de dos fases: secado y cocción. En la fase de secado se utiliza como medio de calentamiento aire caliente y consta de tres etapas, y en la fase de cocción se utiliza como medio de calentamiento vapor saturado y consta de dos etapas. En ambas etapas los medios de calentamiento fluyen en dirección axial al producto. Los cambios de etapa se hacen sin remover el producto del horno de manera automática mediante un sistema de control que abre los pasos de vapor y aire al sistema.
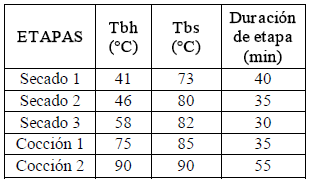
En la tabla 1 se encuentran las condiciones de temperatura de bulbo seco (Tbs) y de bulbo húmedo (Tbh) y el tiempo que dura cada una de las etapas del proceso térmico utilizado para el experimento. Estas etapas corresponden a la práctica habitual de producción de cárnicos, fundamentado de las características organolépticas que se quieren definir en el producto [4].
Tabla 1. Programa de proceso térmico
Table 1. Thermal process Schedule
2.1.3 Medición de la temperatura
Con el fin de seguir el cambio de la temperatura en dirección radial durante el tiempo del proceso se utilizaron termocuplas tipo K ubicadas en dirección radial y a la misma altura en el cilindro a 0.7, 2.3, 4.7, 6.4 y 7.3 cm del centro del producto. Estos sensores fueron conectados a una tarjeta de almacenamiento de datos (Fluke Hydra Series Data Logger) que permite el almacenamiento de los valores de la temperatura cada treinta segundos en un computador.
Dada la consistencia del producto en las etapas iniciales, cuando se encuentra en estado de emulsión, y por la importancia de mantener los sensores en los puntos definidos durante todo el proceso térmico, fue necesario diseñar un soporte mecánico que mantuviera los sensores alineados con el eje principal de la barra.
2.1.4 Medición de la humedad
Para modelar la pérdida de peso del producto a lo largo del proceso se llevo a cabo una medición del contenido de humedad durante el proceso térmico. Las mediciones se realizaron tomando muestras a diferentes radios del producto, sobre distintas barras de igual geometría, peso y composición, para diferentes tiempos del proceso térmico.
Inicialmente se tomaron muestras cada 20 minutos durante los primeros 120 minutos. En esta primera fase es imposible la toma de muestras en diferentes radios, ya que la muestra se comporta como un fluido. Transcurridos los primeros 120 minutos la consistencia del producto permite la toma de muestras en anillos cilíndricos de diferente diámetro ( 2 cm, 3 cm, 4cm, 5.2 cm) y a una frecuencia de 10 minutos entre muestras, así hasta el final del proceso.
El contenido de humedad fue analizado por medio de un analizador de infrarrojo cercano (FoodScan®).
3. PLANTEAMIENTO DE LOS MODELOS
3.1 Transferencia de calor
Para describir la conducción de calor en la barra, se parte de la ecuación general de Fourier en coordenadas cilíndricas (Incropera y De Witt 1999):
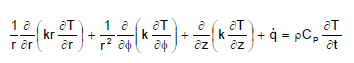
La transferencia de calor del medio circundante al producto de geometría cilíndrica se plantea bajo los siguientes supuestos:
- El producto cárnico cilíndrico es homogéneo.
- La transferencia de calor se da sólo en dirección radial.
- La formación de piel no afecta el valor de las propiedades físicas.
- La distribución del contenido de humedad inicial es uniforme
Bajo estas suposiciones, la transferencia de calor se puede representar mediante la ecuación diferencial [7].
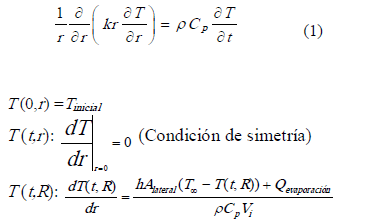
Donde:
T: temperatura (°C)
k: conductividad térmica (W/m°C)
ρ: densidad (Kg/m3)
Cp: capacidad calorífica (J/Kg°C)
R: Radio del cilindro (m)
r: coordenada cilíndricas (m)
El método para el cálculo de la difusividad térmica propone utilizar la ecuación (2) que describe la conducción de calor a lo largo del eje longitudinal de una barra (Eje x). [6]
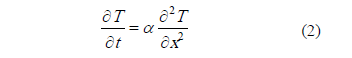
El parámetro a fue ajustado utilizando datos experimentales y de acuerdo con el método experimental descrito por Ochoa en [6] dicha solución es mejorada mediante una búsqueda numérica usando un algoritmo de optimización basado en gradiente que minimiza la diferencia entre los valores de temperatura del modelo y los datos recogidos de acuerdo al método experimental descrito por Ochoa. En todas las fases del proceso se asume que la difusividad térmica varia muy poco ya que hay poca variación en la humedad del producto y esta no varía significativamente con la temperatura como lo mostraron Choi & Okos [8].
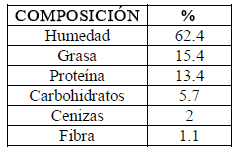
Para el cálculo de Cp y ρ se utilizó el modelo empírico propuesto por Choi & Okos [8] que permite calcular el valor de las propiedades termofísicas con los datos de composición y temperatura. La composición utilizada para el cálculo de las propiedades termofísicas del producto se muestra a continuación:
Tabla 2. Composición del producto
Table 2. Product composition
Con el valor de la difusividad y el de la capacidad calorífica se calcula el valor de la conductividad térmica utilizando la siguiente ecuación
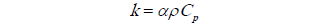
Una vez obtenido el valor de estos parámetros se discretiza el modelo en cuatro capas y se hace un balance de energía para la capa mas externa del producto (capa 1) y se despeja el valor del coeficiente de convección h.
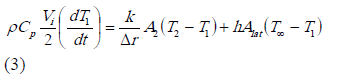
en la ecuación (3) representa el balance de energía de la capa externa donde V1, T1 representan respectivamente el volumen y la temperatura de la capa 1, T2 la temperatura de la capa 2, Tamb la temperatura del ahumadero y A2 es el area de contacto entre las capas 1 y 2.
3.2 Transferencia de humedad
Se planteó inicialmente como mecanismo para describir la pérdida de humedad, el descrito por la siguiente ecuación [9].
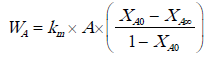
Donde
km: coeficiente de transferencia de masa (Kg/m2s)
A: área de la superficie del producto (m2)
XA0: presión de vapor de agua en la barra
XA∞: presión de vapor de agua en el aire circundante
Sin embargo, como se verá más adelante las mediciones de humedad no permiten el ajuste de los parámetros de la ecuación anterior. De esta manera el mecanismo de transferencia de masa se estima sobre la base de las diferencias de temperatura entre una barra ideal sin pérdida de masa y la temperatura de una barra en proceso. Dicho valor se puede estimar utilizando el balance de energía de la última capa.
4. RESULTADOS
4.1 Transferencia de humedad
A partir de los datos obtenidos en el análisis experimental se puede ver en la Figura 1, que sólo en la parte más externa del producto (línea marrón de puntos), se puede apreciar una pérdida de humedad significativa mientras que los datos de humedad del interior del producto no presentan una diferencia significativa.
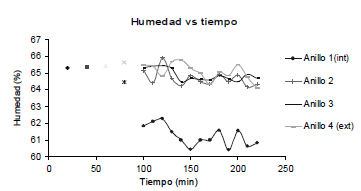
Figura 1. Evolución de la humedad en las distintas capas a lo largo del proceso térmico del producto
Figure 1. Moisture evolution along the radial layers during the thermal process
4.2 Transferencia de calor
Durante el proceso térmico la transferencia de calor entre el medio y la parte externa del producto se realiza por convección, mientras que en el interior del producto el calor se transfiere por conducción. En la Figura 2 se muestran los resultados experimentales del cambio de la temperatura radial durante todo el tiempo del proceso.
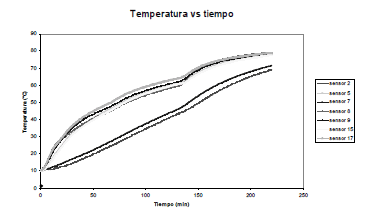
Figura 2a. Evolución de la temperatura en las distintas capas a lo largo del proceso térmico del producto
Figure 2a. Temperature evolution along the radial layers during the thermal process

Figura 2b. Ubicación de los sensores a lo largo de la barra
Figure 2b. Sensors locations along the radial in the product
4.3 Estimación de parámetros
La difusividad térmica se calculó usando el método experimental sugerido por Ochoa [6]. Este método consiste en la medición de la temperatura del producto a distancias e intervalos de tiempo conocidos. Luego, mediante un balance de energía en estado transitorio, se calcula el valor de la difusividad térmica del producto. En este procedimiento se toman datos de temperatura cada 30 segundos hasta que se alcanza el equilibrio térmico.
Los coeficientes de convección se estimaron utilizando las mediciones del proceso y ajustando los parámetros del modelo en cada una de las fases de secado (h1) y de cocción (h2).
4.4 Resultados de la simulación
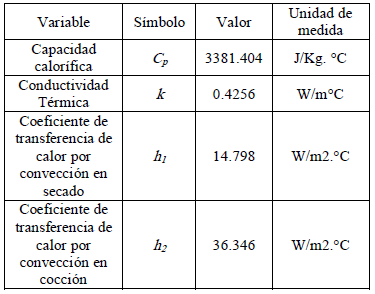
Para simular el modelo se realizó una implementación usando Simulink de Matlab®. Esta herramienta se utilizó ya que permite interactuar fácilmente con el modelo estableciendo condiciones de frontera y graficando de manera eficiente cualquier cambio o experimento realizado sobre el modelo. De igual manera Simulink incluye una integración estrecha con herramientas de optimización que permiten ajustar parámetros de manera directa sin la necesidad de programar nuevas rutinas. El método numérico utilizado para simular el modelo corresponde al método de paso variable Dormand-Prince [10]. Para esta simulación se utilizó el valor de los parámetros que se listan en la Tabla 3 calculados utilizando los métodos anteriormente citados:
Tabla 3. Valor de los parámetros del modelo
Table 3. Model parameters
Los resultados de la simulación del modelo se presentan en la Figura 3. En esta figura la línea inferior (azul) corresponde al comportamiento de la temperatura en el centro del producto mientas que la línea superior (cyan) corresponde al comportamiento de la temperatura durante el proceso térmico en la superficie del producto. Las líneas roja y verde representan la temperatura del producto en dos diámetros interiores del producto: 6 y 8 cm respectivamente.
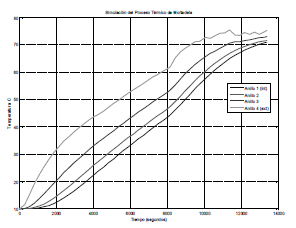
Figura 3. Resultados de la simulación del modelo
Figure 3. Model simulation results
En la Figura 4 se presentan los resultados experimentales y la simulación realizada con el modelo propuesto.
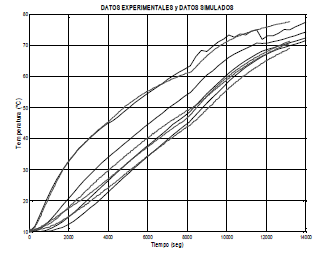
Figura 4. Validación gráfica del modelo. Modelo simulado (líneas negras), datos experimentales (magenta)
Figure 4. Graphic validation of the model. Simulated model (black lines) experimental results (magenta)
5. DISCUSIÓN
Por medio de los ensayos realizados se obtuvieron resultados que permiten un mejor entendimiento del proceso a modelar y de paso comprender mejor los fenómenos que se presentan al interior del producto que se somete al tratamiento térmico.
La Figura 4 muestra como el modelo propuesto representa bien los datos experimentales y ofrece la oportunidad de predecir el perfil de temperatura en diferentes capas ubicadas a lo largo del radio del producto.
Los resultados de la migración de humedad durante el proceso térmico obtenidos por el analizador de infrarrojo cercano, muestran que la diferencia de humedad para diferentes radios al interior del producto no es significativa respecto al total de humedad que se pierde durante el proceso. Sin embargo, en la superficie del producto se puede observar que el contenido de humedad es significativamente menor que en el interior del mismo. La pérdida de humedad en la superficie facilita la coagulación de proteínas y formación de una capa semipermeable (piel del producto) que evita la migración de humedad de las capas interiores al medio.
La aplicación Simulink utilizada para la simulación del modelo permitió generar bloques que optimizan el valor de los parámetros mediante la comparación de la simulación con los datos experimentales. Esto permite que el modelo se ajuste cada vez mejor logrando una representación mas precisa del proceso bajo estudio.
6. CONCLUSIÓN
El modelo planteado describe el fenómeno de transferencia de calor que se presenta entre el medio circundante (al interior del ahumadero) y el producto cárnico emulsificado de geometría cilíndrica que se somete a tratamiento térmico. Por medio de este modelo se pueden diseñar y evaluar los procesos térmicos de los productos cárnicos de geometría cilíndrica. El modelo deberá ser ajustado a nuevas condiciones externas (diferente ahumadero o unidad de enfriamiento) mediante la estimación de un nuevo coeficiente de convección h.
Este modelo permite el diseño y control del tratamiento térmico aplicado a los productos cárnicos. El uso de este tipo de modelos abre las puertas a nuevas metodologías de procesos, productos y condiciones de los equipos, permitiendo optimizar los procesos desde el punto de vista energético y de reducción de tiempos de operación, sin afectar las condiciones del producto.
Es recomendable investigar aún más lo que sucede con efectos como la migración de humedad desde el centro el producto y la coagulación de las proteínas en función de la temperatura usando instrumentos más sensibles y precisos.
REFERENCIAS
[1] WANG, L Y SUN, D. Recent developments in numerical modeling of heating and cooling processes in the food industry - a review, Food science and technology; 14, 408-423, 2006 [ Links ]
[2] BAKALIS, S. Modelling thermal processes: heating, En: Food process modeling (Eds. LMM Tijskens, MLATM Hertog, y BM Nicolai ), CRC Press, 2000 [ Links ]
[3] SEPÚLVEDA, D.R Y BARBOSA-CÁNOVAS, G.V. Heat transfer in food products, En: Transport phenomena in food processing. (Eds. Welti-Chanes, J; Vélez-Ruiz, J.F. y Barbosa-Cánovas, G.V.), CRC Press, 2003 [ Links ]
[4] AMÉZQUITA, A Y RESTREPO, D. Tratamientos térmicos en productos cárnicos, En: Industria de Carnes.(Eds. D. Restrepo; C. Arango; A. Amézquita y R. Restrepo), 2001. [ Links ]
[5] THIPPAREDDI, H Y SANCHEZ, M. Thermal processing of meat products, En: Thermal food processing: new technologies and quality issues. (Ed. D. Sun), CRC Press, 2006 [ Links ]
[6] OCHOA O. Características termofísicas de la carne [PhD. Tesis].Medellín, Universidad Pontificia Bolivariana, 2005 [ Links ]
[7] INCROPERA, F.P Y DE WITT, D.P. Fundamentos de transferencia de calor, Prentice Hall, Naucalpan de Juárez, 1996 [ Links ]
[8] CHOI Y OKOS. Effects of temperature and composition on the thermal properties of foods (Eds M. L. Maguer y P. Jelen), Elsevier Science Publishing Co, pp. 93-101, 1986. [ Links ]
[9] BIRD, R.B; STEWART, W.E Y LIGHTFOOT, E.N. Fenómenos de Transporte, Reverté, Mexico, 1992. [ Links ]
[10] DORMAND, J. R.; PRINCE, P. J. (1980), "A family of embedded Runge-Kutta formula", Journal of Computational and Applied Mathematics 6 (1): 19-26 [ Links ]














