Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.165 Medellín fev./mar. 2011
AUTÓMATA ESTOCÁSTICO HÍBRIDO Y SIMULACIÓN DE MONTE CARLO PARA LA PREDICCIÓN DE LA SEGURIDAD DE FUNCIONAMIENTO DE UN SISTEMA DINAMICO
STOCHASTIC HYBRID AUTOMATON AND MONTE CARLO SIMULATION FOR THE DEPENDABILITY PREDICTION OF A DYNAMIC SYSTEM
GABRIEL ANTONIO PÉREZ CASTAÑEDA
CRAN CNRS UMR 7039, Nancy-Université, France, Instituto Tecnológico de Tehuacan
JEAN-FRANÇOIS AUBRY
CRAN CNRS UMR 7039, Nancy-Université, France jean-francois.aubry@ensem.inpl-nancy.fr
NICOLAE BRINZEI
CRAN CNRS UMR 7039, Nancy-Université, France
Recibido para revisar septiembre 1 de 2009, aceptado diciembre 18 de 2009, versión final enero 15 de 2010
RESUMEN: Un sistema dinámico híbrido es descrito por un conjunto de variables continuas y un conjunto de eventos discretos interactuando mutuamente. Ciertos eventos o variables toman un carácter estocástico. Por tal motivo, se deben tomar en cuenta las fallas de los componentes o las incertidumbres sobre el conocimiento del sistema. En este artículo se presenta la evaluación de los parámetros de la seguridad de funcionamiento por simulación de Monte Carlo dentro del contexto de la fiabilidad dinámica. El sistema es modelizado a través de un autómata estocástico híbrido. El método es ilustrado a través de un caso representado por el sistema de regulación de la temperatura de un horno.
PALABRAS CLAVE: fiabilidad dinámica, autómata estocástico híbrido, simulación de Monte Carlo, seguridad de funcionamiento.
ABSTRACT: A dynamic hybrid system is described by a set of continuous variables and a set of discrete events interacting together. Some events or variables take a stochastic character. Therefore, it is necessary to taking into account component failures or uncertainties on knowledge on the system. In this paper is presented the evaluation of dependability parameters by Monte Carlo simulation in a context of dynamic reliability. For this, the system is modeled by a stochastic hybrid automaton which has been previously formally defined. This approach is illustrated on a test case represented by the regulation temperature system of an oven.
KEYWORDS: dynamic reliability, stochastic hybrid automaton, Monte Carlo simulation, dependability.
1. INTRODUCCIÓN
Una característica importante de numerosos sistemas industriales es que su comportamiento, por ejemplo la respuesta a una perturbación, cambia en función del tiempo debido a las interacciones que existen entre sus componentes o con su medio que lo rodea. Cada comportamiento dado del sistema es definido por las leyes de la física que le son propias. El paso de un comportamiento a otro puede ser debido a varias causas: intervención humana, acción del sistema de control actuando bajo la influencia de variables físicas que describen el estado del sistema (detección de una alarma), una discontinuidad propia al sistema (diodo en un circuito, acoplamiento intermitente) o inclusive una falla de algún componente (dando como consecuencia un mal funcionamiento en el sistema). Por lo tanto, además del carácter híbrido del sistema (aspecto continuo más eventos discretos), es necesario tomar en cuenta su carácter estocástico impuesto por las fallas de los componentes del sistema [1].
Con el fin intervenir en la evaluación predictiva de la Seguridad de Funcionamiento (SdF) de sistemas, como los antes mencionados, cuya estructura fiabilística cambia con el tiempo ha sido necesario introducir el concepto de fiabilidad dinámica. El principal objetivo de la fiabilidad dinámica es tomar en cuenta e integrar los siguientes aspectos [2-4]:
- Las interacciones dinámicas existentes entre los parámetros físicos (representadas generalmente por variables continuas) y el comportamiento nominal o disfuncional de los componentes (representado generalmente por la ocurrencia de eventos).
- El carácter determinista o estocástico de los eventos y de las variables físicas.
- La estructura fiabilística que cambia en el tiempo (re-configuración del modelo).
- Los modos de envejecimiento múltiples de los componentes según el estado discreto del sistema.
- Los modelos no binarios del comportamiento de los componentes.
- El instante y el orden de ocurrencia de los eventos asociados a los cambios del estado discreto, los cuales están relacionados a las fallas de los componentes o al cruce de los umbrales de las variables continuas.
Las herramientas clásicas de la SdF (árboles de fallas, árboles de eventos, diagramas y redes de fiabilidad, etc.) no pueden tomar en cuenta estos aspectos debido a que soportan, en general, una estructura invariante en el tiempo para el sistema y además no toman en cuenta el orden de ocurrencia de los eventos que conducen al estado de peligro. La complejidad matemática de la evaluación analítica de la SdF es tal que sólo es posible bajo ciertas hipótesis o cuando el sistema no es demasiado complejo [2,5]. Otros métodos han sido propuestos [1-3,5-8], sin embargo, éstos difieren en términos de hipótesis, de modelos y de métodos de cálculo. Estos métodos modelizan explícitamente la evolución de las variables físicas y la influencia mutua entre el comportamiento estocástico (fallas de componentes) y determinista del sistema.
En consecuencia, se ha decidido explorar la vía de la simulación del comportamiento completo del sistema, como una alternativa bastante viable. Para esto, se debe establecer un modelo de tipo estado-transición capaz de resolver las ecuaciones diferenciales asociadas a los estados. No se han retenido como modelo las redes de Petri (RdP) porque no se ha encontrado un software que integre en un mismo ambiente la ejecución interactiva de una RdP y un potente resolvedor numérico de ecuaciones diferenciales. Esta situación ha llevado a definir y a implementar en un ambiente adecuado un Autómata Estocástico Híbrido (AEH). Es un autómata porque está compuesto de un conjunto de estados discretos. Es híbrido porque cada estado discreto está definido por un sistema de ecuaciones continuas y un subconjunto de transiciones de salida definidas por umbrales en términos de estas variables continuas. Es estocástico porque cada estado discreto está definido por un conjunto de variables aleatorias y un subconjunto de transiciones de salida definidas por umbrales en términos de las variables aleatorias. En este aspecto reside la originalidad y la importancia del AEH ya que éste toma en cuenta, por un lado, los diferentes modos de funcionamiento continuos del sistema, los cuales están definidos en los diferentes estados del autómata y por el otro lado, el paso de un modo al otro debido a los eventos deterministas o estocásticos designados por las transiciones correspondientes. Los eventos deterministas son producidos por el cruce de umbrales de las variables continuas. Los eventos estocásticos son producidos por un generador aleatorio, en función de las leyes de probabilidad.
El artículo está organizado de la siguiente manera: en la sección 2 se presenta la descripción del método. En la sección 3 se presenta la definición del AEH. En la sección 4 se presenta la aplicación del AEH a la evaluación predictiva de la SdF de un sistema de regulación de la temperatura de un horno. En la sección 5 se presentan los resultados de la simulación de Monte Carlo aplicada al sistema mencionado así como la evaluación de los índices de la SdF del sistema. Finalmente, en la sección 6 se presentan las conclusiones y perspectivas sobre el método presentado.
2. DESCRIPCIÓN DEL MÉTODO
Con la ayuda del AEH se podrá realizar una simulación de Monte Carlo del comportamiento funcional y disfuncional del sistema con el fin de acceder a la evaluación de los indicadores de la SdF. Para lograr esto, primeramente se debe describir el comportamiento del sistema a través del AEH determinando los parámetros concernientes del autómata. Enseguida, se implementa el autómata en el ambiente informático creado para este fin. Posteriormente se efectúa la simulación de Monte Carlo del sistema cuya duración dependerá de dos condiciones: la primera, corresponde a la precisión relativa de cálculo sobre las variables a evaluar y, la segunda, a la probabilidad para que el total de historias efectuadas asegure un resultado con la precisión dada. Finalmente, se efectúa el tratamiento estadístico con los datos obtenidos con el fin de determinar los parámetros correspondientes de la SdF. El método será ilustrado a través de un caso representado por el sistema de regulación de la temperatura de un horno.
3. AUTÓMATA ESTOCÁSTICO HÍBRIDO
Con el fin de integrar los aspectos que demanda la fiabilidad dinámica y acceder, por simulación, a su evaluación, el AEH ha sido formalmente definido en [4,9] sobre la base de la teoría de los autómatas de estados finitos [10] y sobre la teoría de los autómatas híbridos [11-13].
El Autómata Estocástico Híbrido se define como:
AEH = 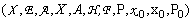 (1)
(1)
en donde
X es un conjunto finito de estados discretos {x1 , x2 ,., xm},
E es un conjunto finito de eventos deterministas o estocásticos {e1,.,er},
X es un conjunto finito de variables reales que evolucionan en el tiempo, siendo x el vector de las variables: x = [x1,., xm]T.
A es un conjunto finito de arcos de la forma (x,e,G,R,x') donde:
x y x' son los estados discretos origen y final del arco k; ej es el evento asociado al arco k; Gk la condición de guarda sobre X en el estado discreto x y Rk es la función de reinicialización de X en el estado x', A es una función de "actividades", que asocia a un elemento de 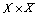 una función definida sobre
una función definida sobre 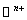 y de valores en
y de valores en 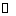 (
(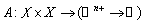 .
.
H es un conjunto finito de relojes sobre 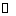 .
.
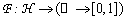 es una aplicación que asocia a c ada reloj una función de distribución.
es una aplicación que asocia a c ada reloj una función de distribución.
P = [pil] es una matriz de las distribuciones de probabilidades donde pil es una distribución de probabilidades de transición de estado 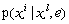 (probabilidad de pasar del estado discreto l al estado discreto i cuando el evento e ha ocurrido). Por ejemplo, si se tiene el mismo evento eq definiendo las transiciones del estado discreto xl hacia los estados discretos x1 , x2 , ., xj (se dice que hay j transiciones en conflicto, el autómata de estados finitos en consideración no sería entonces determinista), se puede definir la probabilidad p1l de pasar del estado xl al estado x1, la probabilidad p2l de pasar del estado xl al estado x2 y la probabilidad pjl de pasar del estado xl al estado xj, con p1l + p2l +.+ pjl = 1.
(probabilidad de pasar del estado discreto l al estado discreto i cuando el evento e ha ocurrido). Por ejemplo, si se tiene el mismo evento eq definiendo las transiciones del estado discreto xl hacia los estados discretos x1 , x2 , ., xj (se dice que hay j transiciones en conflicto, el autómata de estados finitos en consideración no sería entonces determinista), se puede definir la probabilidad p1l de pasar del estado xl al estado x1, la probabilidad p2l de pasar del estado xl al estado x2 y la probabilidad pjl de pasar del estado xl al estado xj, con p1l + p2l +.+ pjl = 1.
x0, X0 y pi0 corresponden respectivamente al estado discreto inicial, al valor inicial del vector de estado continuo en el estado discreto inicial y a la distribución inicial de probabilidades de transición en el estado inicial discreto.
Los elementos X, E y A del AEH corresponden al autómata de estados finitos que definen su parte discreta. Por otro lado, X, A, R y G definen su parte continua. H corresponde a su aspecto temporal y finalmente F y P expresan su aspecto estocástico. El AEH, implementado en el ambiente de simulación del software libre Scicos de Scilab [14], está constituido de tres componentes: un autómata, un generador aleatorio y un descriptor de modos (figura 1).
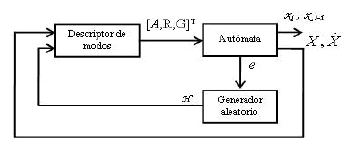
Figura 1. Implementación del autómata estocástico híbrido
Figure 1. Stochastic hybrid automaton implementation
El autómata es un bloque Scicos [13] constituido de i entradas situadas al lado izquierdo del bloque y sólo dos salidas ubicadas al lado derecho. El autómata tiene tantas entradas como estados discretos existen en el sistema. La salida superior del autómata proporciona el vector que contiene el estado discreto corriente xi y el anterior x(i-1). La salida inferior aporta el vector de las variables de estado continuo X y sus derivadas 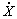 . En la parte inferior del bloque del autómata se tiene una salida correspondiente a los eventos discretos e. Esta salida es activada cada vez que una transición se produce implicando un cambio de estado discreto en el sistema.
. En la parte inferior del bloque del autómata se tiene una salida correspondiente a los eventos discretos e. Esta salida es activada cada vez que una transición se produce implicando un cambio de estado discreto en el sistema.
El descriptor de modos corresponde a las diferentes dinámicas continuas del sistema. Existen tantas dinámicas continuas como estados discretos tiene el sistema. El descriptor de modos tiene dos entradas: la primera corresponde a las variables físicas y a sus derivadas que vienen del autómata. La segunda proporciona, a los estados discretos concernientes, los valores aleatorios producidos por el generador aleatorio.
El descriptor de modos tiene i salidas, las cuales están definidas por el vector [A,G,R]T.
El generador aleatorio corresponde a la estructura temporizada estocástica H y P de la ecuación (1). Cada vez que una transición de estado discreto se produce, la salida de eventos discretos e del autómata genera un evento activando el bloque generador aleatorio à través de su entrada ubicada en la parte superior del bloque. En este instante el generador produce los valores aleatorios que son proveídos a los estados concernidos del sistema, con fin de definir las transiciones estocásticas.
4. SISTEMA DE REGULACIÓN DE LA TEMPERATURA DE UN HORNO
4.1 Descripción del sistemaEl sistema contiene dos lazos de regulación (figura 2). El primero lazo, contiene un controlador Proporcional-Integral (PI) el cual tiene como rol controlar la temperatura del horno en función de la temperatura de referencia. El segundo lazo es del tipo Todo o Nada (TON) y permite mantener la temperatura del horno alrededor de la temperatura de referencia +/-DT. Los dos lazos no pueden funcionar al mismo tiempo. Por tal razón, un relevador o relé cambia sus contactos permitiendo de esta manera activar el PI o el TON. La orden de cambio es dada por el componente "sistema de detección" el cual tiene también la función de detectar las fallas y las reparaciones.
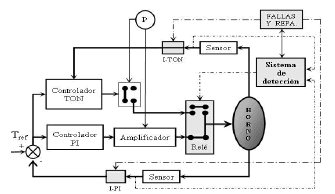
Figura 2. Diagrama estructural del sistema de regulación de la temperatura de un horno
Figure 2. Structural diagram of the temperature control system of an oven
El sistema funciona de la siguiente manera: al inicio la temperatura x del horno es controlada por el controlador PI. Al cabo de un cierto tiempo aleatorio, el controlador falla (interruptor I-PI abierto) con un índice de falla lPI, como consecuencia, la temperatura del horno aumenta rápidamente. El sistema de detección detecta que la temperatura del horno alcanza un valor de peligro (
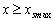 ) deduciendo así que la temperatura del horno está fuera de control. El sistema de detección da la orden al relevador de cambiar de lazo hacia el TON. El lazo del controlador PI está ahora abierta y el lazo del TON cerrado. La temperatura del horno es ahora controlada por el TON (
) deduciendo así que la temperatura del horno está fuera de control. El sistema de detección da la orden al relevador de cambiar de lazo hacia el TON. El lazo del controlador PI está ahora abierta y el lazo del TON cerrado. La temperatura del horno es ahora controlada por el TON (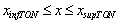 ). Desde que el sistema de detección ha detectado que la temperatura del horno está fuera de control ha dado la orden de cambiar al relevador hacia el lazo del TON activando el proceso de reparación del PI (se considera una reparación de duración aleatoria mPI). Sin embargo, la posibilidad de falla del TON existe (interruptor I-TON abierto), después de una duración igualmente aleatoria (lTON). Una vez que el controlador PI es reparado (interruptor cerrado), el sistema de detección cambia el relevador hacia el lazo de éste y abre el lazo del TON. La temperatura del horno es de nuevo regulada por el controlador PI. Se incluye igualmente el proceso de reparación del TON (lTON). Se considera que el horno no sufre ninguna falla. El AEH de la figura 3 resume el comportamiento del sistema.
). Desde que el sistema de detección ha detectado que la temperatura del horno está fuera de control ha dado la orden de cambiar al relevador hacia el lazo del TON activando el proceso de reparación del PI (se considera una reparación de duración aleatoria mPI). Sin embargo, la posibilidad de falla del TON existe (interruptor I-TON abierto), después de una duración igualmente aleatoria (lTON). Una vez que el controlador PI es reparado (interruptor cerrado), el sistema de detección cambia el relevador hacia el lazo de éste y abre el lazo del TON. La temperatura del horno es de nuevo regulada por el controlador PI. Se incluye igualmente el proceso de reparación del TON (lTON). Se considera que el horno no sufre ninguna falla. El AEH de la figura 3 resume el comportamiento del sistema. 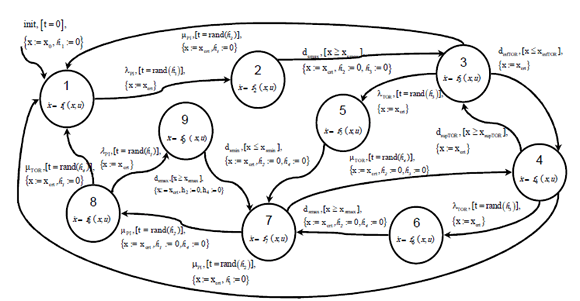
Figura 3. Autómata estocástico híbrido del sistema del horno controlado en temperatura. Por cada transición las condiciones de guarda están indicadas entre corchetes y las reinicializaciones entre llaves.
Figure 3. Stochastic automaton hybrid of the oven system controlled in temperature. For each transition the garden conditions are indicated in square brackets and the resets by braces.
Una breve descripción del AEH con respecto a los estados discretos del sistema es dada a continuación:
Estado 1: el controlador PI está activo y controla la temperatura del horno.
Estado 2: el controlador PI está activo pero ha sufrido una falla. Sin embargo, el controlador TON no ha sido solicitado.
Estados 3 y 4: el controlador TON está ahora activo y el controlador PI está en reparación.
Estados 5 y 6: el controlador TON sufrió una falla pero aún está activo. Cabe mencionar, que el tiempo de detección de la falla del controlador TON es muy breve y la ocurrencia del evento "fin de reparación del PI" durante este tiempo es altamente improbable. En consecuencia, ignoramos la ocurrencia de este evento durante la estancia del sistema en los estados 5 y 6.
Estado 7: la falla del TON es detectada por el sistema de detección. En este estado los dos lazos son inactivos debido a las fallas de los controladores. Sin embargo, al mismo tiempo están los controladores en reparación.
Estado 8: el TON está en proceso de reparación. El controlador PI ha sido reparado y está nuevamente activo.
Estado 9: el PI ha sufrido una falla, pero sigue activo, mientras que el TON está en proceso de reparación.
Las transiciones 2→3, 3→4, 4→3, 5→7, 6→7 y 9→7 son deterministas, ellas corresponden a los cruces de los umbrales de la temperatura. Las otras transiciones son aleatorias: fallas o reparaciones de los controladores.
Aplicando la definición del AEH al sistema de regulación de la temperatura del horno, se tienen las siguientes expresiones:
X = {1,2,3,4,5,6,7,8,9}
E={lPI,lTON,mPI,mTON,dsmin,dsmax,dinfTON,dsupTON}
donde
lPI, lTON, mPI ymTON son respectivamente los índices de falla y de reparación del PI y del TON.
dsmin y dsmax son los umbrales máximo y mínimo de temperatura. Si la temperatura del horno cruza estos umbrales, el sistema de detección identifica las fallas de los controladores PI y TON.
dinfTON y dsupTON son los umbrales de temperatura del TON. Cuando la temperatura del horno es controlada por el TON, si la temperatura cruza uno de estos umbrales, el sistema de detección hará que el horno funcione o deje de funcionar.
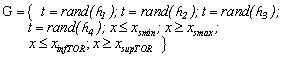
X = {x}, representa la variable física del sistema: la temperatura.
A : X×X→{f1,f2,f3,f4,f5,f6,f7,f8,f9}
R = {x = xcrt}. El valor de la temperatura x a la entrada de cada estado discreto es el mismo que cuando el sistema quita el estado discretoanterior (temperatura corriente). R = {h2:=0} representa el reinicio del reloj h2 que modeliza el tiempo de reparación del controlador PI.
H = {h1,h2,h3,h4}, h1 y h2 representan respectivamente los tiempos de buen funcionamiento y de reparación del controlador PI. Asimismo, h3 y h4 representan los tiempos de buen funcionamiento y de reparación del controlador TON.
F(h) =1 - e-lh. Se ha utilizado la ley exponencial para i=1,.,4.
4.3 Parámetros para la modelación y la simulaciónDesde el punto de vista de la fiabilidad, el sistema tiene dos componentes: el controlador PI y el controlador TON. Los índices de falla y de reparación son constantes (distribución exponencial). Los parámetros utilizados en la simulación son:
xsmax = 240 °C; xsmin = 140 °C
xinfTOR = 170 °C; xsupTOR = 210 °C
lPI = 13.10-05 hrs-1; lTOR = 8.10-05 hrs-1
mPI = 21.10-03 hrs-1; mTOR = 14.10-03 hrs-1
Las ecuaciones diferenciales asociadas a los diferentes estados discretos son:
Estados 1 y 8:
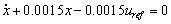 (2)
(2)
Estados 2, 4, 6 y 9:
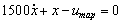 (3)
(3)
Estados 3 y 5:
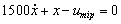 (4)
(4)
Estado 7:
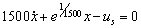 (5)
(5)
en donde:
uref = 190°C, temperatura de referencia
umap=300°C, temperatura a potencia máxima
umip=25°C, temperatura a potencia mínima
us=25°C, temperatura ambiante
5. RESULTADOS
5.1 Modelo y simulación del sistema dinámico
La figura 4 muestra la implementación del modelo Scicos del sistema dinámico del control de la temperatura del horno cuyo comportamiento es presentado en la figura 3. En la figura se observan los 9 bloques que conforman el descriptor de modos, un bloque por cada estado discreto. En cada salida de cada estado discreto se tiene el vector [A,R,G]T. Para ver su implementación en Scicos, se puede referir a [4,8].
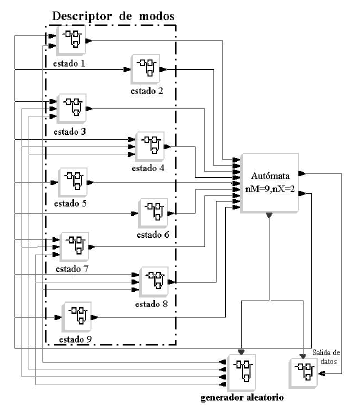
Figura 4. Modelo Scicos del sistema dinámico híbrido
Figure 4. Scicos model of the hybrid dynamic system
La figura 5 presenta una parte de la simulación del sistema. La curva superior muestra la evolución del estado discreto del sistema en función del tiempo. La curva inferior muestra la respuesta del sistema a la temperatura de referencia al inicio de la simulación; enseguida la falla del lazo del PI (en t1) identificada por el cruce del umbral de peligro (en t2), posteriormente la regulación del TON (de t2 a t3). Se puede ver también la falla del TON en t3. La temperatura aumenta de nuevo hacia el umbral de peligro (en t4) lo cual es detectado por el sistema de detección cambiando el relevador a la posición de seguridad. El autómata está en el estado discreto 7, donde ningún controlador controla la temperatura del horno. El horno se encuentra, por lo tanto desconectado, y la temperatura cae hacia la temperatura ambiente hasta que concluye la reparación del controlador PI (en t5). Entonces, el controlador retoma el control de la temperatura del horno. Desde luego que la reparación del TON pudo haberse dado antes que la del PI.
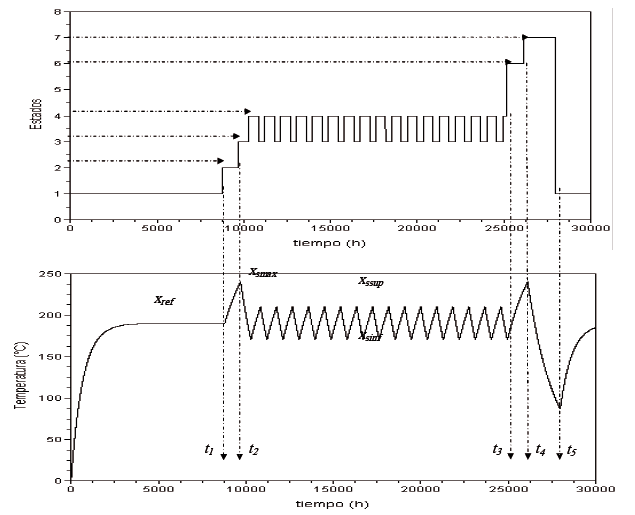
Figura 5. Simulación del sistema dinámico híbrido con el autómata estocástico híbrido
Figure 5. Dynamic hybrid system simulation with the stochastic hybrid automaton
5.2 Evaluación de los índices de la SdF
La fiabilidad, la disponibilidad, la mantenibilidad y el tiempo promedio de disponibilidad del sistema han sido determinados efectuando una simulación de Monte Carlo a través del AEH. Numerosas herramientas de simulación de Monte Carlo utilizadas en SdF reposan sobre el principio de repetición de un gran número de historias fijas predefinidas. Los resultados pueden entonces depender de este número. Se ha preferido utilizar un criterio de convergencia en lugar de un número máximo de historias a repetir. El paro de la simulación se dará cuando dos condiciones sean verificadas:
la contribución de la i-ésima historia simulada con respecto a la precedente (i-1)-ésima historia sea de un valor insignificante. La ecuación (6) expresa este criterio:
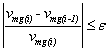 (6)
(6)
donde 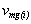 y
y 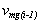 representa n el valor promedio del índice de SdF medido después de i e (i-1) historias simuladas, respectivamente. e es la precisión de cálculo deseada.
representa n el valor promedio del índice de SdF medido después de i e (i-1) historias simuladas, respectivamente. e es la precisión de cálculo deseada.
la precisión e sea verificada un número suficiente de veces k con respecto al total i de historias simuladas. La ecuación (7) expresa este criterio.
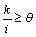 (7)
(7)
Los valores que serán utilizados en las simulaciones para e y q son: e = 0.01 y q = 0.9.
5.2.1 La fiabilidad del sistema
Para el estudio de la fiabilidad del sistema, consideramos suficiente el cálculo del MTTF (Mean time to failure), es decir, la duración promedio de funcionamiento del sistema antes de su primera falla. Para esto en la simulación de Monte Carlo se considera absorbente el estado 7 del AEH de la figura 3. La fiabilidad del sistema es la probabilidad que éste se encuentre en los estados 1, 2, 3, 4, 5 ó 6. Por lo tanto, se aproxima el MTTF por el promedio del tiempo de acceso al estado absorbente 7 (PromTAEA) sobre el conjunto de historias simuladas (una historia es el paso del sistema, desde el estado inicial, por una secuencia de estados de buen funcionamiento antes de llegar al estado de falla, el estado 7). La simulación de Monte Carlo efectuada, cuando las condiciones expresadas por (6) y (7) son verificadas, arroja un valor de:
MTTF = 2.056×106 horas
Los resultados manifiestan que no es necesario hacer más de 630 historias para satisfacer los criterios dados (figura 7). La duración de la simulación es del orden de 17 minutos.
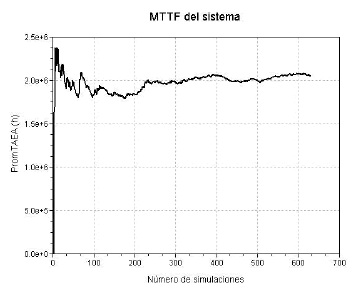
Figura 7. Tiempo promedio de acceso al estado de falla
Figure 7. Mean time of access at the state of failure
5.2.2 La disponibilidad del sistema
La disponibilidad del sistema es la probabilidad que el sistema esté en estado de cumplir una función requerida en las condiciones dadas en un instante de tiempo dado. La disponibilidad ha sido determinada a través de la indisponibilidad asíntota 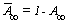 . El estado 7 es el estado de indisponibilidad del sistema. En este estado los controladores PI y TON ya no controlan la temperatura del horno. Para aproximar la disponibilidad asíntota, se ha considerado como medida el tiempo promedio de estancia en el estado de indisponibilidad (TpromEEI) y las condiciones de paro (6) y (7). Cada vez que el sistema entra al estado 7 se verifican si las condiciones son satisfechas. Cuando las condiciones son verificadas, el régimen asintótico es alcanzado, entonces se determina la indisponibilidad del sistema
. El estado 7 es el estado de indisponibilidad del sistema. En este estado los controladores PI y TON ya no controlan la temperatura del horno. Para aproximar la disponibilidad asíntota, se ha considerado como medida el tiempo promedio de estancia en el estado de indisponibilidad (TpromEEI) y las condiciones de paro (6) y (7). Cada vez que el sistema entra al estado 7 se verifican si las condiciones son satisfechas. Cuando las condiciones son verificadas, el régimen asintótico es alcanzado, entonces se determina la indisponibilidad del sistema 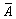 como la relación entre el tiempo de estancia acumulado en el estado de indisponibilidad (estado 7) y el tiempo de estancia acumulado en todos los estados, incluyendo el estado de indisponibilidad. Así, la disponibilidad del sistema es:
como la relación entre el tiempo de estancia acumulado en el estado de indisponibilidad (estado 7) y el tiempo de estancia acumulado en todos los estados, incluyendo el estado de indisponibilidad. Así, la disponibilidad del sistema es:
A∞= 99.99%
Los resultados muestran que sólo es necesario efectuar 870 historias y la duración de simulación es del orden de 39 minutos. La figura 8 presenta el tiempo promedio de estancia en el estado de indisponibilidad.
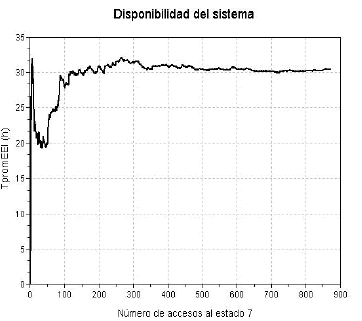
Figure 8. Tiempo promedio de estancia en el estado de indisponibilidad
Figure 8. Mean time of stay in state of unavailability
5.2.3 La mantenibilidad del sistema
La mantenibilidad es la aptitud de un componente a ser restablecido en el instante t en un estado en el cual pueda cumplir una función requerida, sabiendo que está descompuesto desde el instante inicial. Se ha calculado el MTTR (mean time to repair) como la esperanza matemática de la duración de reparación. Por lo tanto, el MTTR se ha aproximado por el promedio del tiempo de acceso a los estados de funcionamiento (PromTAEF) sobre el conjunto de historias simuladas (una historia es el paso del sistema del estado de falla 7 hacia los estados de buen funcionamiento 1 y 4). La simulación de Monte Carlo efectuada para la medida PromTAEF que aproxima de manera asíntota el MTTR, cuando las condiciones (6) y (7) son verificadas, dio como resultado un:
MTTR = 28.26 horas
Los resultados muestran que sólo es necesario efectuar 820 historias (figura 9). La duración de la simulación es del orden de 4 segundos.
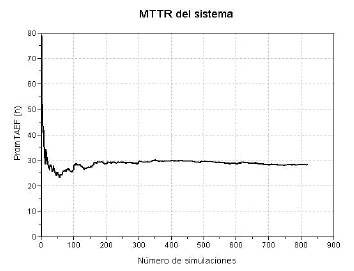
Figure 9. Tiempo promedio de acceso al estado de funcionamiento
Figure 9. Access mean time at the functionality state
5.2.4 El tiempo promedio de disponibilidad
El tiempo promedio de estancia del sistema en los estados de buen funcionamiento (MUT, mean up time) ha sido también calculado por simulación. El MUT del sistema es:
MUT=2.027×106 horas
6. CONCLUSIONES Y PERSPECTIVAS
El método presentado e ilustrado por el caso del sistema de regulación de la temperatura de un horno ha permitido acceder a la evaluación de los indicadores de la SdF a través de una simulación de Monte Carlo. El sistema dinámico ha sido modelizado por el AEH el cual ha permitido pilotear durante la simulación no solamente el comportamiento determinista sino también el comportamiento estocástico del sistema. También ha sido posible visualizar los cambios de estado discreto durante el curso de la simulación. Los tiempos de simulación son aceptables tomando en cuenta las características medianas de la computadora utilizada. Se utilizaron valores constantes para los índices de falla y de reparación de los controladores, sin embargo, los aspectos relacionados con las leyes de envejecimiento con dependencia eventual en el estado discreto o las características estocásticas del sistema de detección serán tomados en cuenta en trabajos posteriores. Se ha considerado también aplicar el AEH al control por supervisión como una herramienta de la SdF.
REFERENCIAS
[1] Zhang, H., Gonzalez K., Dufour F. Dutuit Y. Piecewise deterministic Markov processes and dynamic reliability. Journal of Risk and Reliability. Vol. 222, number 4/2008. [ Links ]
[2] Labeau, P. E., Smidts C., Swaminathan S. Dynamic reliability: towards an integrated platform for probabilistic risk assessment. Reliability Engineering and Systems Safety 68, pp. 219 - 254, 2000. [ Links ]
[3] Cocozza-Thivent, C., Eymard, R. Algorithmes de fiabilité dynamique. Congreso Lambda-Mu 15. Lille, France, 2006. [ Links ]
[4] Pérez Castañeda, G. A. Évaluation par simulation de la sureté de fonctionnement de systèmes en contexte dynamique hybride [thèse doctoral]. Nancy, Francia, Institut National Polytechnique de Lorraine, 2009. [ Links ]
[5] Belhadj, M., Aldemir, T. Some computational improvements in process system reliability and safety analysis using dynamic methodologies. Reliability Engineering System Safety 52, pp. 339 - 347, 1996. [ Links ]
[6] Marseguerra, M., Zio, E., Devooght, J., Labeau, P. E. A concept paper on Dynamic Reliability via Monte Carlo Simulation. Mathematics and Computers in Simulation 47, pp. 371-382, 1998. [ Links ]
[7] Tombuyses, B., Aldemir, T. Computational efficiency of the continuous cell-to-cell mapping technique as a function of integration schemes. Reliability Engineering and System Safety 58, pp. 215-223. 1997. [ Links ]
[8] Tchangani, A.P., Noyes, D. Modeling dynamic reliability using dynamic Bayesian networks, Journal Européen des systèmes automatisés, Vol. 40, No. 8, 2006, pp. 911-935. [ Links ]
[9] Pérez Castañeda, G. A., Aubry, J. F., Brinzei, N. Automate stochastique hybride appliqué à la fiabilité dynamique. 7ème Conférence International de Modélisation et Simulation. Paris, France, 2008. [ Links ]
[10] Cassandras, C. G., Lafortune, S. Introduction to discrete event systems. Kluwer Academic Publishers, 2008. [ Links ]
[11] Alur, R., Courcoubetis, C., Henzinger, T. A., Ho, P. H. Hybrid automata: an algorithmic approach to the specification and verification of hybrid systems. In Grossman, R. L., Nerode, A., Ravn, A. P., Rischel H., editors, Hybrid Systems I. Lecture Notes in Computer Science 736, pp. 209-229, Spinger-Verlag, 1993. [ Links ]
[12] Henzinger, T. A. The theory of hybrid automata, Proceedings of the 11th Annual IEEE Symposium on Logic in Computer Science (LICS), pp. 278 - 292, 1996. [ Links ]
[13] Najafi, M., Nikoukhah, R. Modeling Hybrid Automata in Scicos, Multi-conference on Systems and Control (MSC), Singapore , 2007. [ Links ]
[14] Campbell, S. L., Chancelier, J.-P. and Nikoukhah R. Modeling and simulation in Scilab/Scicos. Springer, 2006. [ Links ]














