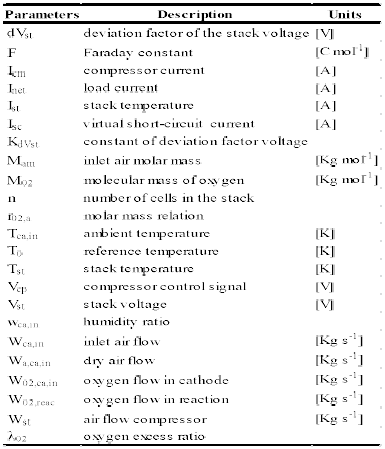
Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.78 no.166 Medellín Apr./June 2011
NON-LINEAR STATE SPACE MODEL AND CONTROL STRATEGY FOR PEM FUEL CELL SYSTEMS
MODELO NO LINEAL EN EL ESPACIO DE ESTADO Y UNA ESTRATEGIA DE CONTROL PARA CELDAS DE COMBUSTIBLE PEM
RICHARD RIOS
Universidad Nacional de Colombia, GAUNAL, Medellín, rriospa@unal.edu.co
CARLOS RAMOS
Universidad Nacional de Colombia, GAUNAL, Medellín, caramosp@unal.edu.co
JAIRO ESPINOSA
Universidad Nacional de Colombia, GAUNAL, Medellín, jairo.espinosa@iee.org
Received for review June 11th, 2010, accepted August 6th, 2010, final version September, 7th, 2010
ABSTRACT: This paper presents a non linear state space model and a linear control system for a Polymer Electrolyte Membrane fuel cell. The dynamics modeled are the temperature of the stack and the air flow compressor, and their main feature is the reproduction of the oxygen excess ratio behavior. The linear control system is a linear quadratic state feedback regulator and a Kalman filter, where the control objective is to avoid oxygen starvation and to minimize fuel consumption, through the tracking of an optimal load power profile. The Kalman filter is designed in order to obtain information from some non-measurable states.
KEYWORDS: PEM fuel cells, oxygen excess ratio, state space model, state space control, Kalman filter, phenomena-based model.
RESUMEN: Este artículo presenta un modelo no lineal en el espacio de estado y un sistema de control lineal para una celda de combustible de Membrana de Intercambio Protónico. El modelo tiene como dinámicas la temperatura de la pila y el flujo de aire, y su principal rasgo es la reproducción del comportamiento de la razón de exceso de oxigeno. El sistema de control lineal es un regulador optimo cuadrático y un filtro de Kalman, cuyo objetivo de control es evitar el agotamiento de oxigeno y minimizar el consumo de combustible, a través del seguimiento de un perfil optimo de potencia de carga. El observador es diseñado con el fin de obtener una completa información de los estados.
PALABRAS CLAVE: Celdas de Combustible de Membrana de Intercambio Protónico-PEM, Exceso de razón de oxigeno, Modelo en el espacio de estado, Control en el espacio de estado, Filtro de Kalman, Modelamiento fenomenológico.
1. INTRODUCTION
Fuel cells are promising energy sources that produce an electrical current with almost null pollutant emissions. One of the most interesting fuel cells types is the Proton Exchange Membrane (PEM) due to its low operating temperature, high efficiency, and low electrolyte corrosion [1]. However, the operating conditions of PEM fuel cells must be regulated to achieve high efficiency in energy transformation and to protect the membrane from degradation [2]. Several works have been developed for obtaining mathematical models for PEM fuel cells: detailed non-linear models in state space [3], empirical polynomial-based approximations [4], model of efficiency based on interpolation and experimental characterization [5], control-oriented models ([6]-[8]), and also models that consider the stack with its auxiliary systems ([9]-[10]). However, those PEM fuel cell modeling approaches are not suitable for state space control purposes since they are based on complex interactions that make it difficult to analyze in a closed form. This issue has been addressed by linearizing those models around a desired operating point for applying linear, non-linear, fuzzy, and other control approaches, as recently described in [11], [12]. Another approach for fuel cell control design is to identify a linear model from process input/output data [13], [14]. Therefore, a non-linear state space model intended for control design and expressed in a classical structure, which also allows performing control synthesis, is desirable.
Considering a PEM fuel cell, the stoichiometric relation between oxygen and hydrogen supplied to the stack, as well as the consumed oxygen must be regulated to be safe; otherwise, the amount of oxygen required to supply the stack current may not be provided. This phenomenon, called oxygen starvation, causes the degradation of the fuel cell and decrements the power output, in which it frequently requires a shut-down of the fuel cell [15]. Therefore, a main concern with the PEM fuel cell is the regulation of the ratio between the oxygen flow supplied to the cathode and the oxygen consumed in the electrochemical reaction, which must be greater than one in order to avoid the oxygen starvation phenomenon [2]. As a result, a physically-based mathematical model intended to design, simulate, and evaluate control approaches in PEM fuel cells is desirable. Such a model should predict the excess oxygen ratio behavior, and also, it should consider the stack temperature effects on the stack voltage.
The authors of this paper propose a non-linear model expressed in the state space representation, whose dynamics are the temperature of the stack and the flow air in the compressor, in this way allowing us to realistically predict the stack voltage and the excess oxygen ratio behavior. This feature makes the model useful since excess oxygen ratio is critical in the fuel cell control design [2]. The model is validated through a set of experimental data obtained from a 1.2 kW NEXA Power Module, which is widely used by many research groups and is representative of the state of the art in PEM technology [16].
Furthermore, a linear control system is designed to illustrate the usefulness of the proposed model. The main control objective of this controller is to avoid oxygen starvation, while it fuel consumption is minimized by tracking optimal operating conditions [2]. The linear control system consists of a linear-quadratic state feedback regulator and a Kalman filter, where the filter is designed in order to obtain information from some non-measurable states. Both the controller and the observer have been designed by using linearized versions of the model around an operating point.
The rest of the paper is organized as follows: Section 2 gives a brief description of a PEM fuel cell and the 1.2 kW Nexa Power Module used for the validation of the model. Section 3 presents the non-linear model for predicting the oxygen excess ratio, stack voltage, thermal effects, and compressor dynamics. Section 4 describes the linear control system used to prevent oxygen starvation and to reduce fuel consumption. Finally, conclusions of the paper are given in Section 5.
2. DESCRIPTION OF THE FUEL CELL SYSTEM
PEM fuel cells are clean and efficient electrical power generation systems which are currently under intense research efforts. The physical configuration of a typical PEM fuel cell is shown in Figure 1, where the interaction among the stack, the air compressor, the humidifier, the cooling system, the hydrogen supply, and the anode purge valve are depicted. One of the most commonly used fuel cell power systems in research tasks is the Ballard 1.2 kW Nexa Power module, which is composed of a stack of 46 cells with membranes of 110 cm2 and other auxiliary systems.
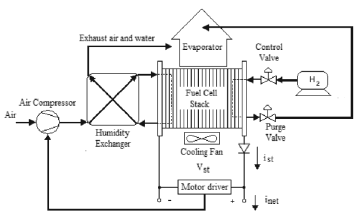
Figure 1. Ballard 1.2 kW Nexa power module diagram
The fuel cell stack produces the current requested by the load and by the ancillary systems, therefore being an auto-powered device. The air compressor generates the cathode airflow required to supply the electrochemical reaction requirements. Similarly, the humidifier and cooling systems provide the appropriate conditions for electricity generation without degrading the fuel cell. In particular, the Nexa system is auto-humidified and its maximum temperature is limited to a high of 65 °C. This prototype uses hydrogen as fuel, and its mechanical circuit is composed of a pressurized hydrogen storage, a control valve to regulate the hydrogen flow, and a purge valve that allows for it to release water particles and inert gases stocked on the anode, that way avoiding the flooding phenomena that degrades power generation [8].
The Nexa system provides run-time measurements of stack temperature, airflow, stack current, and hydrogen consumption, among others. Those variables allow for the run-time calculation of the experimental oxygen excess ratio. Finally, those measurements have been used to identify physical relations among model variables, and also to experimentally validate model predictions and Kalman filter estimations.
3. NON-LINEAR STATE SPACE MODEL
The non-linear state space model proposed in this paper follows the basis given in [8], which proposes the model structure depicted in Figure 2. Such a model’s main equations are described in (1)-(8), and its main dynamics are the stack temperature 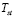 , and the air flow compressor
, and the air flow compressor 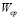 . Using an energy balance, the thermal model obtained for
. Using an energy balance, the thermal model obtained for 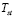 is given by
is given by
 (1)
(1)
where 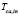 is the ambient temperature,
is the ambient temperature, 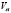 is the stack voltage,
is the stack voltage, 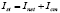 is the stack current,
is the stack current, 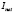 is the load current, and
is the load current, and 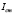 is the compressor current. The stack voltage and compressor current are given by
is the compressor current. The stack voltage and compressor current are given by
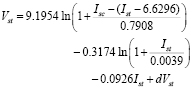 (2)
(2)
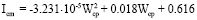 (3)
(3)
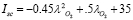 (4)
(4)
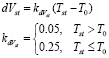 (5)
(5)
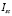 is a virtual short-circuit current, which is parametrized using experimental curves, and it defines the FC polarization curves [2].
is a virtual short-circuit current, which is parametrized using experimental curves, and it defines the FC polarization curves [2]. 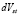 is a deviation factor of the stack voltage, which considers the changes of the stack temperature from the reference temperature
is a deviation factor of the stack voltage, which considers the changes of the stack temperature from the reference temperature 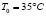 .
. 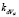 is a constant of deviation factor voltage, and
is a constant of deviation factor voltage, and 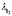 is the oxygen excess ratio. It is important to highlight that (3) was identified experimentally in [8] from the prototype in order to obtain a relation between
is the oxygen excess ratio. It is important to highlight that (3) was identified experimentally in [8] from the prototype in order to obtain a relation between 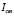 and
and 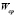 . Similarly, an air flow compressor model
. Similarly, an air flow compressor model 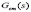 has been obtained by using experimental data taken on the Ballard NEXA 1.2 kW system following the Reaction Curve Method [13],
has been obtained by using experimental data taken on the Ballard NEXA 1.2 kW system following the Reaction Curve Method [13],
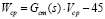 (6)
(6)
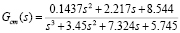 (7)
(7)
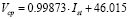 (8)
(8)
where  is the compressor control signal, and its expression for the Ballard NEXA 1.2 kW system, given in (8), has been also identified from experimental measurements.
is the compressor control signal, and its expression for the Ballard NEXA 1.2 kW system, given in (8), has been also identified from experimental measurements.
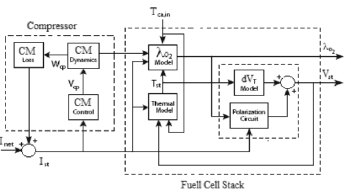
Figure 2. Model structure proposed for PEM fuel cell
For obtaining a state space structure for the model described above, a time domain representation of  is derived as follows:
is derived as follows:
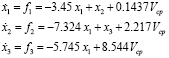 (9)
(9)
where 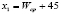 ,
, 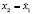 , and
, and 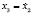 , which are artificial variables introduced to model the compressor. Then, a non-linear state space model is proposed, whose main dynamics, or states, are
, which are artificial variables introduced to model the compressor. Then, a non-linear state space model is proposed, whose main dynamics, or states, are 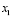 ,
, 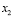 ,
, 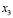 and
and 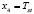 . The inputs of the model are the compressor control signal
. The inputs of the model are the compressor control signal 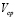 in
in 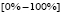 , the load current
, the load current 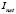 and the ambient temperature
and the ambient temperature 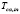 . The outputs are the oxygen excess ratio
. The outputs are the oxygen excess ratio 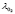 and the stack voltage
and the stack voltage 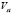 . The model represented in closed form is given as follows:
. The model represented in closed form is given as follows:
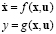 (10)
(10)
where 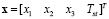 ,
, 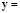
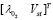 ,
, 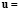
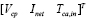 ,
,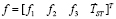 . The output function
. The output function 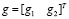 is defined by [8]
is defined by [8]
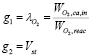 (11)
(11)
where 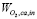 is the oxygen flow that arrives to the cathode and
is the oxygen flow that arrives to the cathode and 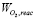 is the oxygen flow consumed in the electricity generation reaction. Using electrochemistry principles,
is the oxygen flow consumed in the electricity generation reaction. Using electrochemistry principles,
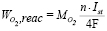 (12)
(12)
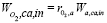 (13)
(13)
is obtained, where 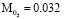 is the molecular mass of the oxygen,
is the molecular mass of the oxygen, 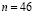 is the number of cells in the stack,
is the number of cells in the stack, 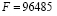 is the Faraday constant,
is the Faraday constant, 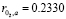 is the molar mass relation between oxygen and dry air, which quantifies the oxygen flow available in the inlet dry air flow
is the molar mass relation between oxygen and dry air, which quantifies the oxygen flow available in the inlet dry air flow 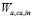 defined by
defined by
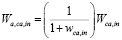 (14)
(14)
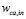 is the humidity ratio, and
is the humidity ratio, and 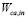 is the inlet air flow defined by
is the inlet air flow defined by
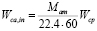 (15)
(15)
where 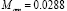 is the inlet air molar mass. It is noted that (14) was used to transform
is the inlet air molar mass. It is noted that (14) was used to transform 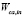 from
from 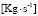 to [SLPM] because
to [SLPM] because 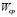 is expressed in such a unit.
is expressed in such a unit.
The non-linear state space model is validated through a set of experimental data from a 1.2 kW NEXA Power Module. The comparison between the experimental data and the model response is presented in Figures 3. In order to provide a measurement of the error between the model and the experimental data, an error analysis is carried out through the Mean Relative Error (MRE) criterion [18], which is given by
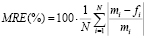 (16)
(16)
where 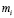 and
and 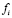 are the experimental and model data, respectively, and
are the experimental and model data, respectively, and 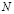 is the number of samples. The application of this criterion gives the following results.
is the number of samples. The application of this criterion gives the following results.
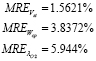 (17)
(17)
Although in the oxygen excess ratio  an error around
an error around  is reached, such results confirm the satisfactory quality of the model for control purposes.
is reached, such results confirm the satisfactory quality of the model for control purposes.
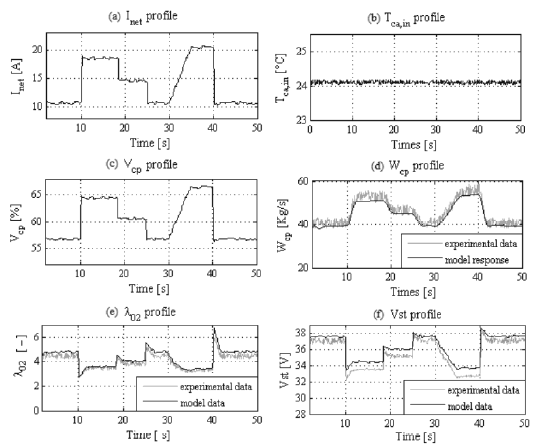
Figure 3. Experimental validation of the non-linear state space model
4. LINEAR CONTROL SYSTEM DESIGN
The linear control system is a Linear-Quadratic Regulator (LQR) and a Kalman filter, where the filter is designed in order to obtain the full information needed for the state feedback. Its control objective is to regulate the oxygen excess ratio 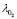 by tracking a given profile, while the fuel consumption described in (18) [2] is minimized.
by tracking a given profile, while the fuel consumption described in (18) [2] is minimized.
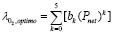 (18)
(18)
where 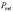 is the net power,
is the net power, 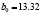 ,
,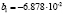 ,
, 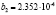 ,
, 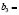
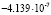 ,
, 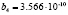 and
and 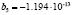 . Figure 4 depicts the structure of the linear control system.
. Figure 4 depicts the structure of the linear control system.
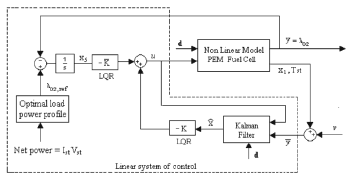
Figure 4. Structure of the linear control system designed for the PEM fuel cell.
The design of the LQR and Kalman filter is based in a linearized version of the model proposed in (10) and (11). The linearization point is described by: 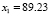 ,
, 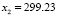 ,
, 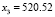 ,
, 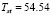 in
in 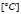 ,
, 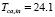 in
in 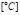 ,
, 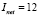 and
and 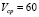 . This operating point was selected taking the values of
. This operating point was selected taking the values of 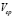 and
and 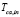 in the middle of the operating range of the experimental data, and taking a value of
in the middle of the operating range of the experimental data, and taking a value of 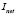 inside of its experimental data range; the rest of the variable values were found by solving (finding a root for) the system of nonlinear equations numerically, described in (10) and (11). The linear model is given by:
inside of its experimental data range; the rest of the variable values were found by solving (finding a root for) the system of nonlinear equations numerically, described in (10) and (11). The linear model is given by:
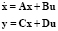 (19)
(19)
where A, B, C, and D are given in (20).
 (20)
(20)
Taking into account that the measurable states are 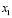 ,
, 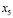 and
and 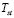 , a Kalman filter is designed for obtaining the full information needed for the state feedback. The linear model used to design the Kalman filter is described as follows:
, a Kalman filter is designed for obtaining the full information needed for the state feedback. The linear model used to design the Kalman filter is described as follows:
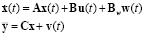 (21)
(21)
where 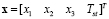 ,
, 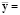
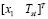 ,
, 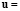
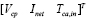 , the matrices
, the matrices 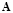 and
and 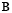 are the same matrices defined in (20), and the matrices
are the same matrices defined in (20), and the matrices 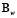 and
and 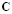 are given by
are given by
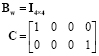 (22)
(22)
The signals 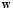 and
and 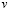 are the plant and measurement noise, and both are assumed to be zero-mean Gaussian processes, that is
are the plant and measurement noise, and both are assumed to be zero-mean Gaussian processes, that is
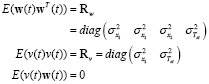 (23)
(23)
where 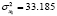 and
and 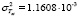 in
in  are the variance of the experimental data of
are the variance of the experimental data of 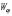 and
and 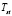 , respectively.
, respectively.
Since the objective of the LQR is to track an optimal load power profile, the linear model is augmented by adding a new state 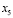 , where
, where 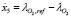 . Given that the LQR is a SISO controller, it holds that the controlled variable is
. Given that the LQR is a SISO controller, it holds that the controlled variable is 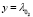 and the manipulated variable is
and the manipulated variable is 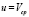 . Then, the linear model used by the LQR is described by (24)
. Then, the linear model used by the LQR is described by (24)
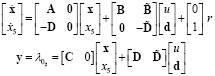 (24)
(24)
where  ,
, 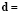
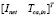 ,
, 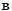 and
and 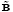 are defined as the first and the rest of the columns of matrix
are defined as the first and the rest of the columns of matrix 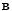 in (20), respectively. In the same way,
in (20), respectively. In the same way, 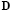 and
and 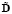 are defined as the first and the rest of the columns of matrix
are defined as the first and the rest of the columns of matrix 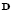 in (20), respectively. Finally, matrix
in (20), respectively. Finally, matrix 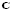 is redefined by the first row of matrix
is redefined by the first row of matrix 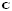 in (20).
in (20).
Since the changes in the environmental temperature are neglected, the disturbance 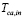 is fixed to the operation point value, and the performance of the linear control system is tested under a current demand profile
is fixed to the operation point value, and the performance of the linear control system is tested under a current demand profile 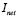 depicted in Figure 5c. The satisfactory simulation performance of the control system is observed in Figures 5 and 6. In addition, a measurement of error between the oxygen excess ratio
depicted in Figure 5c. The satisfactory simulation performance of the control system is observed in Figures 5 and 6. In addition, a measurement of error between the oxygen excess ratio 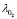 and the reference is given in (25). Furthermore, measurements of the error between the non-linear model and the estimation of the Kalman filter for the state variables
and the reference is given in (25). Furthermore, measurements of the error between the non-linear model and the estimation of the Kalman filter for the state variables 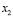 and
and 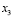 are also given in (25). According to the results, it is clear that oxygen excess ratio
are also given in (25). According to the results, it is clear that oxygen excess ratio 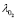 tracks the value of reference given by the optimal load power profile, see Fig. 5a. Also, a good transient response of the oxygen excess ratio
tracks the value of reference given by the optimal load power profile, see Fig. 5a. Also, a good transient response of the oxygen excess ratio 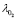 is achieved, in which the settling time is smaller than 10s, which is satisfactory according to the results reported in [2].
is achieved, in which the settling time is smaller than 10s, which is satisfactory according to the results reported in [2].
 (25)
(25)
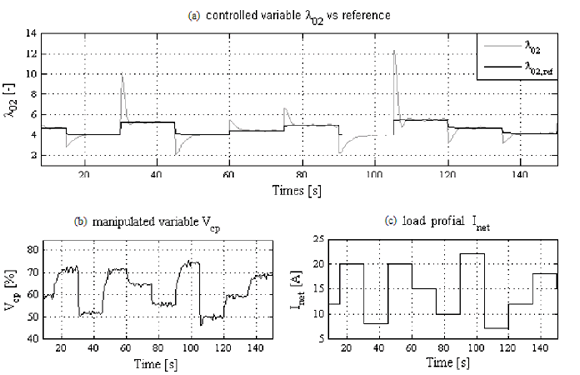
Figure 5. Performance of the linear control system
Another important characteristic of the controller concerns the response of the manipulated variable 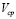 , which remains within the operating interval [0%-100%], without any saturation, under the different changes in the reference caused by the disturbances on
, which remains within the operating interval [0%-100%], without any saturation, under the different changes in the reference caused by the disturbances on 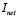 , see Fig. 5b. Finally, it is important to highlight the good estimation offered by the Kalman filter of the non measurable states
, see Fig. 5b. Finally, it is important to highlight the good estimation offered by the Kalman filter of the non measurable states  and
and  , see Fig. 6c y 6d, when this estimation is compared with the value given by the non-linear model of the PEM fuel cell depicted in (10) to (11).
, see Fig. 6c y 6d, when this estimation is compared with the value given by the non-linear model of the PEM fuel cell depicted in (10) to (11).
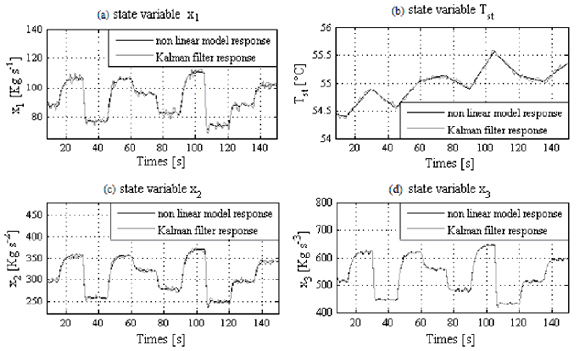
Figure 6. Kalman filter performance.
5. CONCLUSIONS
The authors of this paper propose a non-linear state space model for PEM fuel cells, in which the main dynamics are the temperature of the stack and the compressor airflow. The remarkable feature of the model is the reproduction of the oxygen excess ratio behavior, which was taken into account as a control objective. In addition, the model was used to design a linear control system for a PEM fuel cell system, where the control objective was to avoid oxygen starvation while minimizing fuel consumption, through the tracking of an optimal reference profile. The linear control system showed a satisfactory tracking and transient response, and a good estimation of the non-measurable variables was also achieved.
REFERENCES
[1] Pukrushpan, J., Stefanopoulou, A. and Peng, H. Control of fuel cell breathing, IEEE Control Systems Magazine, 24, 30-46, 2004. [ Links ]
[2] Ramos-Paja, C.A., Bordons, C., Romero, A., Giral, R., and Martinez-Salamero, L. Minimum fuel consumption strategy for PEM fuel cells, IEEE transactions on industrial electronics, 56, 3, 685-696, 2009. [ Links ]
[3] Hernandez, A., Hissel, D. and Outbib, R. Non Linear State Space Modeling of a PEMFE, Fuel Cells, 6,1, 38-46, 2006. [ Links ]
[4] XUE, X., CHENG, K. AND SUTANTO, D. Unified mathematical modelling of steady-state and dynamic voltage-current characteristics for pem fuel cells, Electrochimica Acta, 52, 3, pp. 1135-1144, 2006. [ Links ]
[5] Ogaji, S., Singh, R., Pilidis, P. and Diacakis, M. modeling fuel cell performance using artificial intelligence, Journal of Power Sources, 154, 1, 192-197, 2006. [ Links ]
[6] GOLBERT, J. AND LEWIN, R. Model-based control of fuel cells: regulatory control, Journal of Power Sources, 135, 1-2, 135-151, 2004a. [ Links ]
[7] GOLBERT, J. AND LEWIN, R. Model-based control of fuel cells: optimal efficiency, Journal of Power Sources, 173, 1, 298-309, 2004. [ Links ]
[8] Ramos-Paja, C.A. Fuel cell modelling and control: A power electronics approach, LAP Lambert Academic Publishing, 2010. [ Links ]
[9] KHAN, M.J, AND IQBAL, M.T. Dynamic modeling and simulation of a fuel cell generator, Fuel Cells, 5, 1, 97-104, 2005. [ Links ]
[10] KHAN, M.J, AND IQBAL, M.T. Modeling and analysis of electro -chemical, thermal, and reactant flow dynamics for a pem fuel cell system, Fuel Cells, 5, 4, 463-475, 2005. [ Links ]
[11] AL-DURRA, A., YURKOVICH, S. and GUEZENNEC, Y. Study of non-linear control schemes for an automotive traction PEM fuel cell system, International Journal of Hydrogen Energy, 2010. [ Links ]
[12] PENG, H., GUANG-YI, C., XIN-JIAN, Z. AND MINGRUO, H. Coolant circuit modeling and temperature fuzzy control of proton exchange membrane fuel cells, International Journal of Hydrogen Energy, vol 35, pp. 9110-9123, 2010. [ Links ]
[13] GARCIA-GABIN, W, DORADO, F., AND BORDONS, C. Real-time implementation of a sliding mode controller for air supply on a PEM fuel cell, Journal of process control, vol 20, pp. 325-336, 2010. [ Links ]
[14] METHEKAR, R.N., PATWARDHAN, S.C. RENGASWAMY, R., GUDI, R.D. and PRASAD, V. Control of proton exchange membrane fuell cells using data driven state space models, Chemical Engineering Research and Design, vol 88, pp. 861-874, 2010. [ Links ]
[15] Bordons, C., Arce, A. and del Real, A. Constrained predictive control strategies for PEM Fuel Cells, in Proceeding American Control Conference, 2486-2491, 2006. [ Links ]
[16] REAL, A. J., Arce, A. and bordons, c. Development and experimental validation of a PEM fuel cell dynamic model, Journal of Power Sources, 173, 310-324, 2007. [ Links ]
[17] CAMACHO, E. F. and bordons, c. Model predictive control, Springer, 2da, 2007. [ Links ]
[18] Ramos-Paja, C.A, ROMERO, A., GIRAL, R., VIDAL-Idiarte, e. and Martinez-salamero, l. Fuzzy-based modelling technique for PEMFC electrical power generation systems emulation, in IET Power Electronics, 2, 241-255, 2009. [ Links ]