Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.168 Medellín out./dez. 2011
A GENERAL ANALYTICAL APPROACH FOR PRESTRESSED AND NON-PRESTRESSED CONCRETE BEAM-COLUMNS REINFORCED WITH BONDED AND UNBONDED COMPOSITES: (I) THEORY
METODO ANALITICO GENERAL PARA VIGAS-COLUMNAS DE HORMIGON PREESFORZADO Y NO PREESFORZADO REFORZADAS CON "COMPOSITES" ADHERIDOS Y NO ADHERIDOS: (I) TEORIA
J. A. RODRIGUEZ-GUTIÉRREZ
Structural Engineer, ACCIONA, Madrid, Spain. alfredo1704@gmail.com
J. DARÍO ARISTIZÁBAL-OCHOA
National University, Medellín Colombia jdaristi@unal.edu.co
Received for review August 2nd, 2009; accepted August 11th, 2010; final version December 10th, 2010
ABSTRACT: An analytical method that determines the short and long-term response of prestressed and non-prestressed concrete beam-columns reinforced with any combination of FRP bars or/and plates, steel rebars, bonded and/or unbonded prestressed tendons is proposed. Beams and columns encased with FRP fabrics and FRP tubes filled with concrete are covered with the proposed model. The effects of tension stiffening, creep and shrinkage of the concrete, and the relaxation of the prestressed steel reinforcement are considered. The models proposed by Vecchio and Collins [1] and by Popovics [2, 3] for the stress-strain relationships of the concrete in tension and compression are adopted, respectively. The strain-stress relationships of the steel and FRP reinforcements are modeled using multiple straight lines (polygonal lines). The method of the fibers (modified) is used to calculate the moment-curvature diagrams at different levels of the applied axial load (i.e., the M-P-fcurves), and the Gauss method of integration (for the sum of the contributions of the fibers parallel to the neutral axis) to calculate the lateral rotations and deflections along the span of the beam-column. The validity of the proposed model and corresponding equations were tested against experimental data available in the technical literature (see part II of this publication).
KEYWORDS: Axial load, beam, column, composite materials, concrete-filled tube, high-strength concrete, deflections, fiber reinforced polymers (FRP), prestressed concrete
RESUMEN: Se propone un método de análisis que determina la respuesta a corto y largo plazo de vigas-columnas de hormigón pretensado y no pretensado reforzado con cualquier combinación de barras de FRP y/o placas, barras de acero, torones pretensados adheridos o no adheridos. El método de an álisis propuesto incluye vigas y columnas revestidas con telas FRP y tubos de FRP rellenos de hormigón. También se incluyen los efectos de la rigidez a tracción, fluencia y retracción del hormigón y la relajación de la armadura de acero pretensado. Se adoptan los modelos de Vecchio y Collins [1] y de Popovics [2, 3] en las relaciones esfuerzo-deformaci ón del hormigón a tracción y a compresión, respectivamente. Las relaciones esfuerzo-deformación de los refuerzos de acero y de FRP se modelan mediante líneas rectas múltiples (esto es, líneas poligonales). El mé todo de las fibras (modificado) es utilizado para calcular los diagramas momento-curvatura a diferentes niveles de la carga axial aplicada (es decir, las curvas M-P-f) y el método de Gauss de integración (para la suma de las contribuciones de los fibras paralelas al eje neutro) para calcular las rotaciones laterales y deflexiones a lo largo de la luz de la viga-columna. La validez del modelo propuesto y las ecuaciones correspondientes se pusieron a prueba con datos experimentales disponibles en la literatura técnica (véase la parte II de esta publicación).
PALABRAS CLAVE: Fuerza axial, viga, columna, materiales compuestos, tubos rellenos de hormigón, hormigón de alta resistencia, deflexiones, polímetros reforzados con fibras, hormigón pretensado.
1. INTRODUCTION
The use of FRP materials is of great importance in civil engineering, particularly in the retrofitting of existing structures. This is a consequence of current needs for lighter, more slender, corrosion resistant, and more economical structures. For instance, due to the deterioration, the relatively short life, and high-costs of the maintenance of existing highway structures, the Departments of Transportation (DOTs) all across the USA are very active in the use of composites in construction. In spite of the fact that there is still some reticence in the USA in using these materials, their use is growing little by little due to the low cost of maintenance in comparison with conventional materials. Piers made of FRP tubes filled with concrete, piers encased with FRP wraps, hybrid FRP beams and girders supporting decks also made of composites, rectangular and T-beams reinforced with FRP bars, beams prestressed with bonded or unbonded FRP tendons, and columns prestressed with FRP tendons, are now commonly used. A brief summary of the main uses and research of FRP composites in civil engineering structures is presented next.
Rebars made of FRP. The use of FRP bars as regular reinforcement has been investigated by many researchers. Saadatmanesh [4] studied the effects of the amount of FRP reinforcement and the type of bar shape and surface finish on the actual behavior and response of concrete beams. Thériault and Benmokrane [5] studied the effects of the amount of FRP reinforcement and the concrete strength on the crack width, bending moment resistance, and strains in the concrete and reinforcements. Bogdanovic [6] studied the lateral deflections in beams reinforced with aramid-fiber reinforced polymer (AFRP) bars. Thiagarajan [7] studied the moment-curvature response, bending moment strength, and strains in the concrete and reinforcements in beams reinforced with carbon-fiber reinforced polymer (CFRP) bars.
"Passive" FRP Laminates for Beam Retrofitting. This is perhaps the most common use of FRP composites in construction today. Saadatmanesh and Ehsani [8] and An et al. [9] carried out extensive theoretical and experimental studies on the behavior of rectangular and T-beams reinforced with GFRP laminates. Ross et al. [10] carried out theoretical and experimental studies on beams retrofitted with FRP laminates. Shahawy and Beitelman [11] and Ei-Tawil et al. [12] studied the static and fatigue response of T-beams reinforced with CFRP laminates. Borowicz [13] carried out theoretical and experimental studies on the behavior of rectangular and T-beams reinforced with mechanically applied FRP laminates. Ei-Refaie et al. [14] studied the behavior and response of continuous beams reinforced with FRP laminates. More recently, Rasheed et al. [15] proposed a method to calculate deflections in composite beams subjected to concentrated, uniform, and triangular distributed loads.
Prestressed FRP Laminates and Strands for Beam Retrofitting. Due to current needs for retrofitting existing prestressed concrete buildings and bridges, the use of prestressed FRP Laminates and Strands has received some attention. Sen et al. [16] showed that the actual behavior and response of beams prestressed with FRP strands and laminates are similar to those of prestressed with steel strands. Lees and Burgoyne [17] studied the effects of bonding in beams prestressed with AFRP strands. Grace et al. [18] investigated the behavior of box girders reinforced with bonded and unbonded prestressed CFRP bars and strands. Different techniques for the prestressing of FRP laminates have been proposed by Triantafillou et al. [19], Wight et al. [20], and Yu et al. [21].
FRP/Concrete Hybrid Beams. Deskovic et al. [22] studied the behavior of different forms of GFRP box girders with a concrete deck along the top surface and reinforced with CFRP laminates along the bottom of the girders. Fam and Rizkalla [23] studied the behavior of solid and hollow FRP tubes filled with concrete. Schnerch et al. [24] developed a method for the analysis of rectangular hybrid beam-columns.
Columns Reinforced with FRP. Kawaguchi [25] and Mirmiran et al. [26] experimentally studied the behavior of columns prestressed with FRP bars and strands. Issa et al. [27] studied the behavior of columns reinforced with GFRP tendons. Chaallal and Shahawy [28, 29] studied the behavior of rectangular columns encased with CFRP laminates.
Long Term Loads on Beams Reinforced with FRP. Plevris and Triantafillou [30] studied the long-term response of beams reinforced with FRP laminates. Deskovic et al. [31] studied the long-term response of hybrid beams subjected to sustained loads. Naguib and Mirmiran [32] studied the long-term response of a CFRP tube filled with concrete subjected to sustained loads. Zou [33, 34, 35, and 36] studied the long-term behavior of beams prestressed with FRP strands.
Objectives and Scope. The main objective of this paper is to present an analytical method and a numerical algorithm for the calculation of the short and long-term response of prestressed and non-prestressed concrete beam-columns reinforced with FRP bars or plates, steel rebars, bonded or/and unbonded prestressed tendons. In addition, beams and columns encased with FRP fabrics and FRP tubes filled with concrete are analyzed with the proposed model. The effects of tension stiffening, creep and shrinkage of the concrete, and the relaxation of the prestressed steel are considered. The models proposed by Vecchio and Collins [1] and by Popovics [2, 3] are adopted for the stress-strain relationships of the concrete in tension and compression, respectively. The strain-stress relationships of the steel and FRP reinforcements are modeled using multiple straight lines (polygonal lines). The method of the fibers (modified) is used to calculate the moment-curvature diagrams at different levels of the applied axial load (i.e., the M-P-f curves), and Gauss' method of integration (for the sum of the contributions of the fibers parallel to the neutral axis) to calculate the rotations and lateral deflections along the span of the beam-column. The shear and torsion effects along the member are not included. Due to space limitations, the validity of the proposed method and numerical algorithm is presented in part II of this paper. (over 36 experimental test specimens reported by different researchers were used to verify the proposed method and the numerical algorithm).
2. PROPOSED ANALYTICAL MODEL
The proposed model is an extended and improved version of an algorithm presented previously by Rodriguez-Gutierrez and Aristizabal-Ochoa [37, 38] for the analysis, design, and behavior of slender concrete columns subjected to biaxial bending and axial load. The M-P-f diagrams along the member are calculated using the method presented by Rodriguez-Gutierrez and Aristizabal-Ochoa [37] with the exception of the stress-strain curve of the concrete which is the one presented by Popovics [2, 3] and expressed by Eq. (1a), instead of the parabola of Hognestad (for the ascending part) and the straight line (for the descending part; i.e., Eqs. (3a) and (3b) listed in ref. [37]). It was found that the stress-strain curve given by Eq. (1a) is more appropriate for beam-columns made of high-strength concrete. Expression (1a) includes the simultaneous long-term effects of shrinkage esh(t) and creep eo(t) both of which must be determined beforehand either experimentally or theoretically by the user.
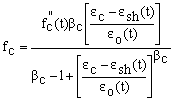 (1a)
(1a)
Where: 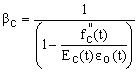 (1b)
(1b)
eo(t) = eo(0)[1+f(t, ti)] (1c)
Ec(t) = Ec(0)/[1+cf(t, ti)] (1d)
maximum stress in the concrete at time t;
Ec(t) = elastic modulus of the concrete at time t;
esh(t) = shrinkage strain of the concrete at time t;
eo(t) = strain in the concrete corresponding to the maximum stress in concreteat time t;
f(t, ti) = creep factor of the concrete;
ti = initial time of application of loading in days;
c = age factor of the concrete.
Any theoretical or experimental expression for f(t, ti) and esh(t) may be used.
The beam-column can be reinforced with combinations of FRP bars or plates, steel rebars, bonded or/and unbonded prestressed tendons all with different stress-strain relationships. Beam-columns made of circular tube sections are modeled as 16-sided polygons (since a larger number of sides does not increase the accuracy significantly).
Calculation of Displacements and Rotations. The method of the fibers (modified) is used to calculate the moment-curvature diagrams at different levels of the applied axial load (i.e., the M-P-f curves), and Gauss' method of integration (for the sum of the contributions of the fibers parallel to the neutral axis) to calculate the rotations and the lateral deflections along the span of the beam-column, as shown in Fig. 1.
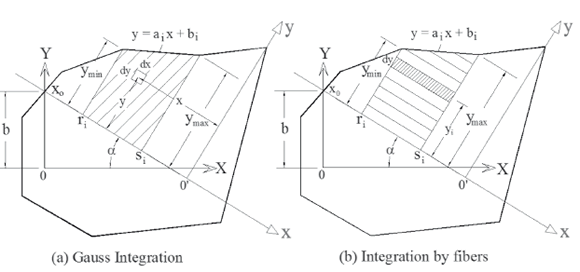
FIG. 1. Cross-section of beam-column subjected to biaxial bending
Consider the beam column AB (shown in Fig. 2) with generalized boundary conditions subjected to an axial load P (with eccentricities ea and eb at A and B, respectively), and subjected to concentrated or distributed transverse loads. The bending moment M(Z) along the member span is as follows:
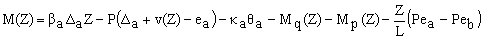 (2a)
(2a)
Where: Mq(Z) and Mp(Z) = bending moment at Z (along the column with pinned-pinned end conditions) caused by the distributed and concentrated loads, respectively; and v(Z) = lateral deflection at Z.
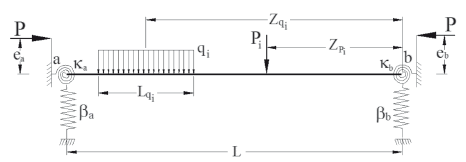
FIG. 2. Model of beam-column with generalized boundary conditions
To obtain M(Z) and v(Z) along the member, both the rotations and lateral deflections at the ends A and B (i.e., qa, qb, Da, Db, respectively) must be determined first. To achieve this, the following four non-linear equations must be solved:
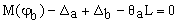 (2b)
(2b)
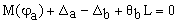 (2c)
(2c)
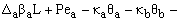
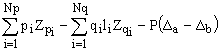 = 0 (2d)
= 0 (2d)
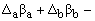
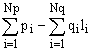 = 0 (2e)
= 0 (2e)
Where: M(ja), M(jb) = moments at ends A and B obtained from the moment-curvature diagrams, respectively; and Da, qa, Db and qb = deflections and rotations at ends A and B, respectively.
An iterative process is proposed to solve Eqs. (2a-e) for qa, qb, Da and Db as follows:
1) Select a set of trial (initial) values for the unknowns qa, qb, Da, and Db;
2) Divide the beam-column into Ne elements (at least 10) and the bending moments are calculated at the Ne+1 sections;
3) Determine the curvatures at the Ne+1 sections using the corresponding M-P-f curves;
4) Calculate M(ja) and M(jb);
5) The four non-linear equations (2b-e) are solved; if the solution is not obtained, the values of the unknowns qa, qb, Da, and Db are corrected using a numerical method (like Newton-Raphson or Runge-Kutta);
6) Return to step 2 and repeat the process until Eqs. (2b-e) are solved;
7) Once Eqs. (2b-e) are solved to a desired level of accuracy, the rotations and lateral deflections of each node are calculated as follows:
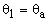 (3a)
(3a)
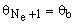 (3b)
(3b)
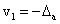 (3c)
(3c)
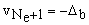 (3d)
(3d)
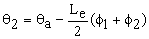 (3e)
(3e)
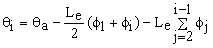 (3 £ i £ Ne) (3f)
(3 £ i £ Ne) (3f)
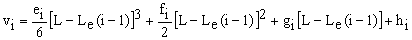 (2 £ i £ Ne) (3g)
(2 £ i £ Ne) (3g)
Where: 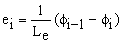 (3h)
(3h)
(3i)
(3j)
(3k)
8) Calculate the second-order moments along the member (P-Delta effects) and return to Step 3. The iterative process is halted when the maximum lateral displacement along the column remains practically unchanged between two consecutive iterations. When this happens, the column is stable under the applied loads; otherwise, the column becomes unstable under the applied loads when the maximum lateral displacement along the column keeps on increasing between two consecutive iterations. The number of iterations required is generally less than 5 but it increases as the beam-column is less stiff and lateral displacements become large.
Notice that the proposed method does not require any assumed curve of the deflected shape of the member like in most other methods.
For the particular case of a simple supported beam-column with zero moments at both ends only Eqs. (2a) and (2b) have to be solved by making Da = Db = 0 with Eq. (2a) reduced to:
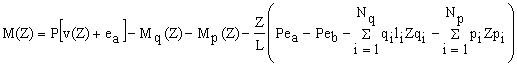 (4)
(4)
For beam-columns reinforced with steel shapes or composites plates, the contributions to the axial load and bending moments with respect to the local xy-axes of the shape or plate-j are given by the following expression:
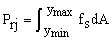 (5a)
(5a)
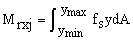 (5b)
(5b)
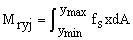 (5c)
(5c)
Using Fig. 3a: 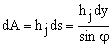 and
and 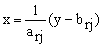 . If the strain-stress relationship of the composite plate-j is modeled using straight lines, the integrals (5a)-(5c) can be expressed as follows:
. If the strain-stress relationship of the composite plate-j is modeled using straight lines, the integrals (5a)-(5c) can be expressed as follows:
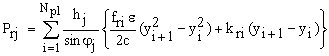 (6a)
(6a)
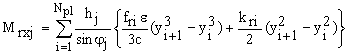 (6b)
(6b)
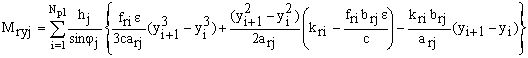 (6c)
(6c)
Where:
Npl = number of straight segments used to represent the stress-strain curve of the composite material, as shown by Fig. 2b;
jj = angle made by the mid-plane of plate-j with the neutral axis of the beam;
arj = tan jj;
hj = thickness of plate-j; and
fri and kri = slope and intersection of a line that describes the stresses along the composite plate-j, respectively.
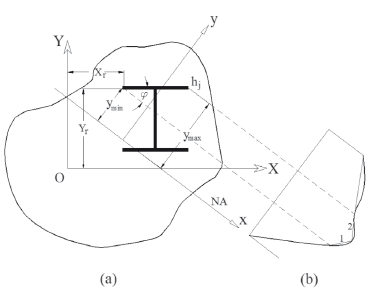
FIG. 3. Stress distribution across an embedded shape
The model by Vecchio and Collins [1] is adopted for the stress-strain relationship for the concrete in tension as described by the following two expressions:
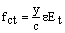 (
(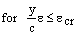 ) (7a)
) (7a)
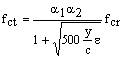 (
(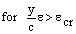 ) (7b)
) (7b)
Where:
fcr = stress of the concrete at cracking (assumed to be equal to
with
in MPa);
y = distance from the extreme fiber in tension to the neutral axis;
c = depth of the neutral axis;
e = strain of the concrete at the extreme fiber in tension;
ecr = strain of the concrete at cracking;
a1 = factor that takes into account the effects of the bonding characteristics of the reinforcement. (= 1 for regular corrugated rebars; = 0.7 for plain bars, wires or bonded strands; = 0.5 for FRP reinforcement; and = 0 for unbonded reinforcement); and
a2 = factor that takes into account the effects of the type of applied loads (= 1 short-term load; and = 0 for long-term and cyclic loads).
CONCLUSIONS
A model is developed that is capable of predicting the short and long-term response of prestressed and non-prestressed concrete beam-columns of any cross section reinforced with FRP bars and/or plates, steel rebars, bonded and/or unbonded prestressed tendons. In addition, beams and columns encased with FRP fabrics and FRP tubes filled with concrete can be analyzed. The effects of tension stiffening, creep and shrinkage of the concrete, and the relaxation of the prestressed steel are considered. The validity of the proposed model and corresponding equations were tested against experimental data available in the technical literature (see part II of this article).
ACKNOWLEDGEMENTS
This research was carried out at the National University of Colombia at Medellín by the GES group. The authors want to express their gratitude to the School of Civil Engineering and DIME for their financial support.
REFERENCES
[1] Vecchio, F.J., and Collins, M. P.,The Modified compression field theory for reinforced concrete elements subjected to shear, ACI Structural Journal, 83(2), 1986, pp. 219-231. [ Links ]
[2] Popovics, S., A review of stress-strain relationships curves for concrete, ACI J., 67(3), 1970, pp. 243-248. [ Links ]
[3] Popovics, S. A, numerical approach to the complete stress-strain curves for concrete, Cement and Concrete. Res., 3(5), 1973, pp. 583-599. [ Links ]
[4] Saadatmanesh, H., Fiber composites for new and existing structures, ACI structural J., 91(3), 1994, pp. 346-354. [ Links ]
[5] Thériault, M., and Benmokrane, B., Effects of FRP reinforcement ratio and concrete strength on flexural behavior of concrete beams, J. of Composites for Construction, ASCE, 2(1), 1998, pp. 7-16. [ Links ]
[6] Bogdanovic, B., Deflection calculations of FRP-reinforced concrete beams, Department of Civil Engineering University of Manitoba, Report 23735, 2002, 23 pp. [ Links ]
[7] Thiagarajan, G., Experimental and analytical behavior of carbon fiber-based rods as flexural reinforcement, J. of Composites for Construction, ASCE, 7(1), 2003, pp. 64-72. [ Links ]
[8] Saadatmanesh, H., and Ehsani, R., RC beams strengthened with GFRP plates I: Experimental Study, J. Struct. Engrg., ASCE, 117(11), 1991, pp .3417-3433. [ Links ]
[9] An, W., Saadatmanesh, H., and Ehsani, R. RC beams strengthened with GFRP plates. II: Analysis and parametric Study, J. Struct. Engrg., ASCE, 117(11), 1991, pp .3434-3455. [ Links ]
[10] Ross, C. A; Jerome, D. M., Tedesco, J. W., Hughes, M. L. Strengthening of reinforced concrete beams with externally bonded composite laminates, ACI structural J., 96(2), 1999, pp. 212-220 [ Links ]
[11] Shahawy, M., and Beitelman, T. E. Static and fatigue performance of RC beams strengthened with CFRP laminates, J. Struct. Engrg., ASCE, 125(6), 1999, pp. 613-621. [ Links ]
[12] Ei-Tawil, S., Ogunc, C., Okeil, A., and Shahawy, M. Static and fatigue analyses RC beams strengthened with CFRP laminates," J. Composites for Construction, ASCE, 5(4), 2001, pp. 258-267. [ Links ]
[13] Borowicz, D. T., Rapid strengthening of concrete beams with powder-actuated fastening systems and fiber reinforced polymer (FRP) composite materials, Thesis submitted in partial fulfillment for the requirements for the degree of Master of Science, University of Wisconsin-Madison, 2002, 128 pp. [ Links ]
[14] EI-Refaie, A. F; Ashour, A. F., and Garrity, S. W., Sagging and hogging strengthening of continuous reinforced concrete beams using carbon fiber-reinforced polymer sheets," ACI structural J., 100(4), 2003, pp. 446-453. [ Links ]
[15] Rasheed, H. A., Charkas, H., and Melhem, H., Simplified nonlinear analysis of Strengthened Concrete Beam based on a rigorous approach. J. Struct. Engrg., ASCE, 130(7), 2004, 1087-1096. [ Links ]
[16] Sen, R., Issa, M., Sun, Z., Shahawy, M. Static response of fiberglass pretensioned Beams, J. Struct. Engrg., ASCE, 120(1), 1994, pp. 252-268. [ Links ]
[17] Lees, J. H., and Burgoyne, C. S., Experimental study of influence of bond on flexural behavior of concrete beams pretensioned with aramid fiber reinforced plastics, ACI structural J., 96(3), 1999, pp. 377-386. [ Links ]
[18] Grace, N. F., Singh, S. B., Shinouda, M. M., and Mathew, S. S. Flexural response of CFRP Prestressed concrete box beams for highway bridges, PCI Journal., 49(1), 2004, pp. 92-104. [ Links ]
[19] Triantafillou, T. C., Deskovic, N., and Deuring, M. Strengthening of concrete structures with prestressed fiber reinforced plastic sheets, ACI Structural Journal, 89(3), 1992, pp. 235-244. [ Links ]
[20] Wight, R. G., Green, M. F., Erki, M-A, Prestressed FRP sheets for post-strengthening reinforced concrete beams, J. of composites for construction, ASCE, 5(4), 2001, pp. 214-220. [ Links ]
[21] Yu, P., Silva, P. F., and Nanni, A Flexural performance of RC beams strengthened with Prestressed CFRP sheets," Center for Infrastructure and Engineering Studies Department of Civil, Architectural, and Environmental Engineering University of Missouri-Rolla Rolla, MO, 65409-0030, 2003, pp. 9. [ Links ]
[22] Deskovic, N., Triantafillou, T. C., and Meier, U. Innovative design of FRP combined with concrete: short-term behavior, J. Struct. Engrg., ASCE, 121(7), 1995,pp. 1069-1078 [ Links ]
[23] Fam, A. Z., and Rizkalla, S. H., Flexural behavior of concrete-filled fiber-reinforced polymer circular tubes, J. Composites for Construction, ASCE, 6(2), 2002, 123-132. [ Links ]
[24] Schnerch, D., Fam, A. Z., Rizkalla, S. H., FRP/Concrete hybrid rectangular tubes, North Carolina State University-CFL Report No 02-03, 42, 2002. [ Links ]
[25] Kawaguchi, K., Ultimate Strength and deformation characteristics of Concrete members reinforced with AFRP rods under combined axial tension or compression and bending," SP-138, ACI, 1993, pp. 671-683. [ Links ]
[26] Mirmiran, A., Yuan, W., Chen, X., Design for slenderness in concrete columns internally reinforced with fiber-reinforced polymer bars, ACI structural J., 98(1), 2001, pp. 116-125. [ Links ]
[27] Issa, M., Sen, R., Mariscal, D., Shahawy, M., Static response of fiberglass pretensioned columns," J. Struct. Engrg., ASCE, 120(12), 1994, pp. 3634-3648. [ Links ]
[28] Chaallal, O., and Shahawy, M., Effect of concrete strength on the Performance of FRP wrapped RC column under combined axial-flexural loading," Technical report, Structural Research Center, Florida Department of Transportation, Tallahassee, 2000, 192 pp. [ Links ]
[29] Chaallal, O., and Shahawy, M. Performance of fiber-reinforced polymer-wrapped reinforced concrete column under combined axial-flexural loading, ACI structural J., 97(4), 2000, pp. 659-668. [ Links ]
[30] Plevris, N., and Triantafillou, T. C., Time-dependent behavior of RC members Strengthened with FRP laminates, J. Struct. Engrg., ASCE, 120(3), 1994, 1017-1042. [ Links ]
[31] Deskovic, N., Meier, U., and Triantafillou, T. C., Innovative design of FRP combined with concrete: long-term behavior, J. Struct. Engrg., ASCE, 121(7), 1995, pp. 1079-1089. [ Links ]
[32] Naguib, W., and Mirmiran, A. Flexural creep test and modeling of concrete-filled fiber reinforced polymer tubes, J. of Composites for Construction, ASCE, 6(4), 2002, pp. 272-279. [ Links ]
[33] Zou, P-X. W., Flexural behavior and deformability of fiber reinforced polymer prestressed concrete beams," J. of Composites for Construction, ASCE, 7(4), 2003, pp. 275-284. [ Links ]
[34] Zou, P-X. W., Long-term deflection and cracking behavior of concrete beams prestressed with carbon fiber-reinforced polymer tendons, J. of Composites for Construction, ASCE, 7(3), 2003, pp. 187-193. [ Links ]
[35] Zou, P-X. W., Flexural behavior and deformability of fiber reinforced polymer prestressed concrete beams, J. of Composites for Construction, ASCE, 7(4), 2003, pp. 275-284. [ Links ]
[36] Zou, P-X. W., Theoretical study on short-term and long-term deflections of fiber reinforced polymer prestressed concrete beams, J. of Composites for Construction, ASCE, 7(4), 2003, pp. 285-291. [ Links ]
[37] Rodriguez, J. A., and Aristizabal-Ochoa, J. D., M-P-f Diagrams for reinforced, partially, and fully prestressed concrete sections under biaxial bending and axial load, J. Struct. Engrg., ASCE, 127(7), 2001, pp .763-773.
[38] Rodriguez, J. A., and Aristizabal-Ochoa, J. D., Reinforced, Partially, and Fully Prestressed Slender Concrete Columns under Biaxial Bending and Axial Load, J. Struct. Engrg., ASCE, 127(7), 2001, pp. 774-783. [ Links ]














