Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.168 Medellín out./dez. 2011
DECISION STRATEGIES FOR EVALUATING PEDESTRIAN ACCESSIBILITY
ESTRATEGIAS DE DECISIÓN PARA EVALUAR LA ACCESIBILIDAD PEATONAL
RODRIGO BOTERO IBARRA
GITTV, Civil and Geomatical Engineering School, Universidad del Valle, Colombia. robotero1@yahoo.es
JACKELINE MURILLO HOYOS
GITTV, Civil and Geomatical Engineering School, Universidad del Valle, Colombia. jackeline.murillo@correounivalle.edu.co
CIRO JARAMILLO MOLINA
GITTV, Civil and Geomatical Engineering School, Universidad del Valle, Colombia. ciro.jaramillo@correounivalle.edu.co
Received for review July 1st, 2010; accepted August 6th, 2010; final version August 26th, 2010
ABSTRACT: Weighted linear combination and ordered weighted averaging mathematical operators were applied in the evaluation of pedestrian accessibility at the Universidad del Valle, Meléndez campus. These operators belong to fuzzy set techniques that permit the evaluation of criteria whose domains are not clearly defined, identifying for these membership levels of selected variables and accepting the aggregation of different types of information. Five evaluation scenarios were considered: pessimistic, moderately pessimistic, neutral, moderately optimistic, and optimistic. For the cartographic visualization of accessibility, the interpolation of the results is carried out by means of the inverse distance weighting method, generating thematic maps for each evaluation scenario. The application of these methods provides an effective tool for the management and analysis of a great range of spatially referenced data in the decision making process.
KEYWORDS: Multicriteria evaluation, ordered weighted averaging (OWA), geographic information systems (GISs), fuzzy set theory
RESUMEN: Se aplicaron los operadores weighted linear combination y ordered weighted average en la evaluación de la accesibilidad peatonal en el campus de la Universidad del Valle, sede Meléndez. Estos operadores pertenecen a un conjunto de técnicas difusas que permiten la evaluación de criterios cuyos dominios no están claramente definidos, identificando para ellos niveles de pertenencia de las variables seleccionadas y admitiendo la agregación de información de diferente naturaleza. Se consideran cinco escenarios de evaluación, pesimista, algo pesimista, neutro, algo optimista y optimista. La aplicación de estos métodos se convierte en una herramienta eficaz en el proceso de toma de decisiones al facilitar la administración y el análisis de una gran variedad de datos espacialmente referenciados. Adicionalmente, se generan mapas temáticos de cada escenario de evaluación para facilitar la visualización e interpretación de las condiciones de accesibilidad en el área de estudio.
PALABRAS CLAVE: Evaluación multicriterio, ordered weighted averaging (OWA), sistemas de información geográfica (SIG), teoría de los conjuntos difusos
1. INTRODUCTION
Within the scope of decision theory, is multi-criteria evaluation (MCE) which can be defined as a set of techniques aimed at assisting the decision-making process, focusing on the need to evaluate criteria to which scores, values, or preference intensities have been assigned.
In this context, decision is defined as the choice of one alternative among several others that represent different locations, classifications, or hypotheses about a phenomenon, considering some criteria or conditions which can be quantified or assessed. Criteria can be factors or exclusions; a factor is a criterion that emphasizes or minimizes the aptitude of a determined alternative, and exclusion, in contrast, is a criterion that limits the aptitude of an alternative. Both factors and exclusions are generally measured on a continuous scale. A decision rule is a procedure by which criteria are combined, using aggregating methods, to obtain the result of an evaluation, leading to the taking of a decision.
Given its characteristics, MCE is a practical tool that permits the analysis of multiple spatially-distributed attributes to determine their incidence on a geographical region, submitted to a decision process. With geographical information systems (GIS) it is possible to implement some MCE techniques, such as the fuzzy techniques derived from the fuzzy sets theory [1]. The GIS environment allows for the integration of models and large numbers of data related with territory and submitting cartography with the results of different evaluation scenarios [2].
There are several types of fuzzy aggregation functions or operators, i.e. intersection operators, union operators, and fuzzy sets averaging operators. A generalization of these three methods is the ordered weighted averaging (OWA) technique, introduced by Yager in 1988. The operators used for the evaluation performed in this article are the weighted linear combination (WLC) and the OWA.
According to the general procedure of MCE, the first step in the evaluation required the identification of the criteria which are assigned a weight in relation to their level of importance. In MCE, the weights are quantitative in character and based on a numerical scale, which is from 0 (the minimal weight) up to 1 (the maximum weight). The next step is the criteria normalization carried out by the fuzzy membership functions, such as the sigmoidal decreasing function and linear function, allowing the different criteria to be compared to each other. The subsequent step in MCE corresponds to the aggregation by the WLC and the OWA methods. Finally, in MCE the global scores are integrated into the GIS, facilitating the visualization and interpretation of results.
2. METHODOLOGY
According to MCE, the methodology indicated in the following sections allows the assessment of pedestrian accessibility.
2.1 Key destinations
The measurement of pedestrian accessibility determines the facility with which the user can access one or several key destinations (KDs) in the university campus. These key destinations are defined as the places that employees, students, etc., frequently visit during their normal activities.
2.2 Definition of criteria
According to Malczewski [3], a general rule for defining the evaluation criteria is that such criteria have to be identified with regard to the problem situation. The criteria set has to be defined in such a way that the number of criteria might not be so large as to be unmanageable, but at the same should not be too small, which would cause an oversimplification of the decision problem. In several cases, the choice of criteria sets depends on the availability of information. At the same time, the choice of criteria has to be based on the desirable attributes that represent the multicriterial nature of the problem. Generally, each attribute should be comprehensible and measurable. Additionally, the attribute set has to be complete, operational, divisible, not redundant, and minimal [4].
The procedure for the definition of criteria has to be an iterative process with multiple steps in which the redundant information must be eliminated through the examination of relevant literature, analytical studies, and expert opinions [2, 3].
Criteria might be factors or exclusions [1], but in this specific research MCE will only take into account the factor criteria due to the fact that the criteria exclusions have not been considered.
With regard to the previous consideration, and once the key destinations have been defined, two groups of concrete values are taken from two different sources: measurements on the network and surveys. From the first source of information the integral route factor indicator is taken (Criterion 1), and the integral tracing speed indicator (Criterion 2), is also taken. From the second source of information, classification by longitude is taken (Criterion 3), and the arrivals-departures number (Criterion 4), is also taken.
Additionally, qualification by key destination was used for assigning a weight to each key destination, thereby indicating the degree of importance that each destination has for the user.
2.3 Weights assignment
The purpose of assigning weights to the criteria is to express the degree of importance for each criterion in relation to the others in the evaluation process.
There are several methods for assigning weights to criteria, among which are the methods based on criteria ranking (ranking methods), score scales (rating methods), score distribution, criteria comparison by pairs (pairwise comparison methods) and tradeoff analysis [5].
The simplest method for the assignment of weights to the criteria is based on the arrangement of criteria (ranking method) which consists of ordering the criteria by rank according to the degree of importance assigned by the evaluator regarding his/her preference. This method is divided into three parts: rank sum, rank reciprocal, and rank exponent. In this evaluation, the rank reciprocal method will be used, defined by:
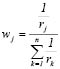 (1)
(1)
Where wj is the criterion weight j, r are the criteria ranks, and the numbers of criteria is n = 4. The weights obtained with this method are w1 = 0.48; w2 = 0.24, w3 = 0.16, and w4 = 0.12, so that their sum is equal to the unit.
2.4 Information normalization
Criteria have been obtained from different sources, therefore their valuation scales are different, and it is not possible to compare them. This is why it is necessary to standardize or normalize them so that their value scales are comparable. Most of the normalization or standardization methods use maximum and minimal values for defining a scale.
The main methods of normalization are linear normalization, z-score, and the normalization method for the application of membership functions to the continuous variables taken from the fuzzy sets theory. This last method is considered here since normalization is equivalent to the fuzzification process in which the degree of membership is defined from an element to a fuzzy set [6]. In fact, the fuzzy set theory provides rich mathematical foundations for understanding decision problems and for the construction of decision rules in criteria evaluation and combination.
There are several types of membership functions: the linear function, sigmoidal (s-shaped) function, j-shaped function, and the function defined for the user [4]. These functions can be increasing or decreasing functions: in the former case, the normalized score increases at the same time that the original value does, whereas in the decreasing functions, the normalized score decreases while the original value increases. These functions map the set of values for each criterion over the [0, 1] interval, in a continuous variation from no membership to the complete membership that corresponds to total accessibility.
Criteria normalization is carried out after the assignment of weights, in order of importance. First, the kind of fuzzy function is selected, and then the limits for the control points that calibrate the normalizations are specified.
Criterias 1, 2, and 3 are each normalized by their characteristics with a sigmoidal function, monotonically decreasing according to (2) and (3):
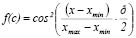 (2)
(2)
When
(3)
Where x is the value of each criterion for each key destination, xmax is the maximum value that is taken by the variable on each criterion, and xmin is the minimal value that x takes, in this case xmin = 0.
The sigmoidal function is reproduced by using a cosine function with four points of inflexion that define the form of the curve. Given that the adopted function is monotonically decreasing, the inflexion points are reduced to only two: a first point that begins at 1 for the minimal values of variables, and a second point that ends at 0 when the variable has the maximum value. According to (3), the function falls to zero, remaining there. All of these functions are calibrated with maximum and minimal values for each criterion, which are used as inflexion points.
Decreasing functions are used by criteria characteristics. By treating the scores that depend on distances, the membership degree of these criteria decreases as its score increases; and sigmoidal functions are selected because these functions favor the short distance with a higher membership degree [5].
Criterion 4, with discrete values, is linearly normalized in an increasing way, given by (4) and (5):
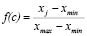 (4)
(4)
When
(5)
The procedure is similar with the increasing linear function, therefore its inflexion points are minimal values when the function begins at zero, and they are maximum when the function ends in the unit.
2.5 Aggregation methods
In the domain of decision theory there are a great number of aggregation operators that are used depending on the problem context. In this case, for combining the criteria, the aggregation operators most relevant in the processes of spatial decision are applied, these being the WLC and OWA [5]. Additionally, an appliance of the WLC method in a GIS environment is shown by Malczewski [3].
The WLC method, known also as the simple additive weighting (SAW) or scoring method [3], is one of the most simple. It combines the factors from a weighted measure. The total score is obtained by multiplying the weight of each criterion by the normalized value of each key destination and performing the summation over partial results, as shown in (6).
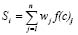 (6)
(6)
Where Si is the final score of each key destination i, wj is the weight of each criterion, and f(c)ij the normalized value of each key destination for each criterion.
An adaptation of this method, which is more similar to the probabilistic additive weighting (PAW) method, is used for evaluation due to the double assignment of weight. A first weight wj, which corresponds with the weight of each criterion, and a second weight, pi, which corresponds to the degree of importance assigned to each key destination by the users, according to the survey, is exposited in (7).
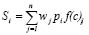 (7)
(7)
The WLC method allows the criteria to be compensated in its attributes (tradeoff); that is, a very poor attribute or quality within a criterion can be compensated by the existence of characteristics that are stronger in other criteria. With an OWA approach, it is possible to control this compensation of criteria and include the effect of the attitude in front of risk; equipping the analyst with the capacity to choose which zones of strategic solution space one desires to locate.
The OWA procedure is a type of aggregation operator that belongs to the group of fuzzy aggregation operators (FAOs), introduced by Yager in 1988 [6], using the concep ts established by Zadeh [1], which provide interesting solution alternatives to the problems of classification that are introduced into a context of imprecise categories, and which consist of a generalization of these operators, providing continuity between the intersection and union, and applying weighted means between these two. In general terms, the OWA is a weighted sum with ordered evaluation criteria [3]. The OWA procedure, by being based on fuzzy sets theory, allows an easy semantic interpretation, using linguistic quantifiers. This aggregation method relies on two types of weights. On one hand, the weights are assigned to each criterion (by degree of importance), and on the other hand are the ordered weights, which allow the direct control over levels of tradeoff among criteria [7].
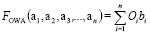 To apply the OWA operator, it is essential to pass through a previous stage of re-ordering criteria (with their respective normalization). For evaluation, the criteria have been ordered from least to greatest. Subsequently, the final score is calculated by applying (8):
To apply the OWA operator, it is essential to pass through a previous stage of re-ordering criteria (with their respective normalization). For evaluation, the criteria have been ordered from least to greatest. Subsequently, the final score is calculated by applying (8):
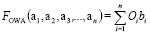 (8)
(8) Where 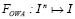 ; and bi is the i-th minor element on the inputs set (ai) that is assumed to belong to the unit interval. Oi the weights are ordered, so that Oi ≥ 0 and SiOi = 1 [8].
; and bi is the i-th minor element on the inputs set (ai) that is assumed to belong to the unit interval. Oi the weights are ordered, so that Oi ≥ 0 and SiOi = 1 [8].
The ordered weights vector is a vector that has the form O = (O1, O2, O3, …, On), whose components Oi can take values into the [0, 1] range. The variation of each component will determine the vectors; and these, in turn, will define each evaluation scenario.
There are three extreme cases in the ordered weights vectors; when the first component is equal to the unit, [1, 0, 0, …, 0]; when the last component is equal to the unit, [0, 0, 0, …, 1]; and when all the components are equal, in which case we have 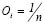 . These cases correspond respectively to the MIN, MAX (of fuzzy sets theory), and AVG operator or average [1, 6].
. These cases correspond respectively to the MIN, MAX (of fuzzy sets theory), and AVG operator or average [1, 6].
The MIN operator is an operator for the intersection of fuzzy sets and corresponds to logical operation AND which produces the greatest group of all possible fuzzy intersections for the same group of given fuzzy sets. This interpretation implies that there is no positive compensation in the membership degree of fuzzy groups in consideration, that is, there is no tradeoff [3]. From a multi-criteria evaluation viewpoint, this extreme case is interpreted as the completely pessimistic case. The MAX operator is an operator for the fuzzy sets union and corresponds to the logical operation OR. This operator produces the smallest of all the possible fuzzy unions for some fuzzy sets groups. Unlike the MIN operator, the interpretation of the OR operator implies the maximum membership degree that is achieved by some of the fuzzy sets under consideration; therefore, there is no tradeoff either [3]. From the multi-criteria evaluation viewpoint, this extreme case is interpreted as the completely optimistic case.
The OWA method used here is performed by taking into account five evaluation scenarios, for each of which the ordered weighted vector is defined firstly. The scenario evaluations are: pessimistic (minimal values of criteria), moderately pessimistic, neutral, moderately optimistic, and optimistic (maximum values of criteria). Each scenario indicates, within the decision theory context, the acceptation level or the degree of risk that the decision maker is able to assume. In this case, it deals with the accessibility level of key destinations. The lowest scores correspond to the lowest accessibility level according to the selected criteria until reaching the highest score that indicates the greatest possible accessibility. The intermediate scores that correspond to the neutral evaluation scenario of the OWA method are equivalent to the evaluation by the WLC method. Table 1 shows the values assigned to the components of the five weighted vectors of the OWA method (each vector corresponds to an evaluation scenario).
Table 1. Ordered weighted vectors.
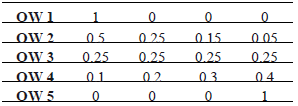
The OWA method permits the integration of numerical data with no numerical data, both of them of different natures. This characteristic converts this procedure, along with the WLC, into a method of powerful analysis with the possibility of being completely integrated into the GIS environment.
For classifying the OWA operators with regard to their position between AND and OR operation, there are four measurements associated with the ordered weights, the ANDness, ORness, tradeoffdispersion (or scattering) [6, 8].
2.6 ANDness, ORness, tradeoff, and dispersion computation
The appliance of the OWA operator has some implications for the MCE. According with ANDness, ORness, tradeoff and dispersion computation can be assumed to be the measure of risk degree involved in the decision. The ANDness and ORness are complementary measurements of risk capacity of the decision-maker; the first case is presented when ANDness and ORness values higher than 0.5 are assumed, accounting for higher pessimism degrees or aversion to risk in the decision process. Other cases can occur when ORness values are higher than 0.5. These account for optimistic decision strategies or those with a higher risk tendency; while ANDness and ORness values equal to 0.5 account for a neutral trend of the decision-maker or the indifference to risk. Within the context of evaluation, the degree of risk will be assumed to be the accessibility degree of each key destination; in this way, a pessimistic evaluation is equivalent to a low accessibility level and its ANDness is maximum, whereas an optimistic evaluation is equivalent to a high accessibility level, determining an ORness maximum as shown in (9) and (10).
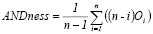 (9)
(9)
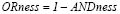 (10)
(10)
Where n is the total number of criteria, i is the i-th criterion, and Oi is the i component of ordered weights vector O [3].
The tradeoff computation is related with the measure of commutativity between the criteria or criteria compensation. There is maximum or total tradeoff when all ordered weight vector components have exactly the same value, that is, they are perfectly equilibrated. The assignment of 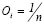 to each of the n, evaluation criteria produces an aggregation according to the arithmetical mean; in this case the criteria are mutually compensated and the result of the OWA procedure is made equivalent to that of the WLC. It can be said that the WLC procedure is a particular case of the OWA procedure. In this work, a maximum or total tradeoff means an accessibility level according to those selected as expressed in (11).
to each of the n, evaluation criteria produces an aggregation according to the arithmetical mean; in this case the criteria are mutually compensated and the result of the OWA procedure is made equivalent to that of the WLC. It can be said that the WLC procedure is a particular case of the OWA procedure. In this work, a maximum or total tradeoff means an accessibility level according to those selected as expressed in (11).
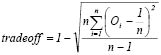 (11)
(11)
Where n is the total number of criteria, i is the i-th criterion, and Oi is the i component of ordered weights vector O [3, 6, 8].
From the results of ANDness and tradeoff computation, the strategic spectrum of decision is obtained in an approximately triangular form, defined on one hand for the attitude to risk, and on the other by the tradeoff level [9].
Another important indicator is the normalized dispersion, similar to the tradeoff, but measuring the “entropy" of ordered weights. This indicator, based on the information theory by Shannon [5, 6], measures how much information is used in each argument, which means that the more disperse the weighted vector is, more information on each criterion is being used in the aggregation process. The dispersion is maximum when the weighted vector corresponds to the arithmetical mean (all of the weighted vector components are equal, all of the criteria are mutually compensated) and dispersion is minimal when one of the weighted vector components is equal to the unit (and the other components are equal to zero). If it is assumed that O ln O = 0, then the normalized dispersion is given by (12):
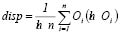 (12)
(12)
Where n is the total number of criteria, i is the i-th criterion, and Oi is the i component of the ordered weights vector O [6,7, 8].
In the case of performed evaluation, the analysis of tradeoff and dispersion represents the capacity that each criterion has for influencing the accessibility degree and the information quantity of each criterion being used to set the global score in the evaluation process, respectively.
3. EVALUATION OF PEDESTRIAN ACCESIBILITY AT THE CAMPUS
The evaluation of pedestrian accessibility was made at the Meléndez university campus. This campus occupies an area of 100 acres, of which about 17% is built on (buildings, pedestrian, and vehicular paths). Movement throughout the campus is had by means of a pedestrian network of approximately 12 km, consisting of sidewalks, paved streets, soil or gravel tracks, ramps, and stairs. This campus has a population of approximately 16,000 people, consisting of students, professors, and employees.
A first analysis is obtained with data evaluation by means of the WLC method which indicates that there is a higher degree of preference or visit frequency for certain key destinations, which does not necessarily imply that they are easily accessible.
For the cartographic visualization of accessibility, the interpolation of the results is made by means of the inverse distance weighting method, generating thematic maps for every method. Figure 1 shows the thematic maps generated for every scenario of evaluation, WLC and OWA.

Figure 1. Thematic maps for accessibility evaluation
For the OWA and WLC evaluation, five evaluation scenarios are defined that begin with the completely pessimistic scenario, with a maximum ANDness equal to the unit, up to the completely optimistic scenario, with a minimal ANDness equals zero. On other hand, maximum ORness equal to the unit corresponds to a completely optimistic scenario, and minimal ORness equal to zero represents the completely pessimistic scenario.
An intermediate scenario in which ANDness and ORness values are equal to 0.5 are considered, meaning that a maximum tradeoff (equals the unit) corresponds to an indifferent evaluation or that it is neutral to risk. This scenario is completely equivalent to the WLC method.
The computation results of ANDness, ORness, tradeoff, and dispersion are shown in Table 2.
Table 2. Risk indicators, OWA method.
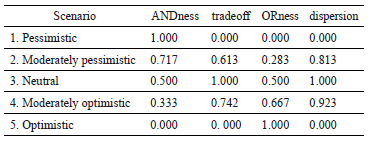
The first scenario depicts the lowest scores within the global qualification, its ANDness being maximum generally indicating the poorest accessibility that can be achieved in this evaluation.
Given that early weights assigned to each criterion and each key destination determines the final score behavior, it can be seen that in the combination with the ordered weights, the third scenario, with maximum tradeoff, supports Criterion 1 influence on the every other criteria, and this, combined with the preference given by the weight of each key destination, favors the accessibility of certain destinations over others.
In the optimistic scenario, the highest scores of accessibility are found in a few key destinations. Therefore, there are few places on the campus where the accessibility is relatively good.
If the scores obtained by WLC aggregation method are compared with the third scenario of the OWA method, the total correspondence between them can be observed. As has been previously mentioned, this occurs because the WLC is a particular case of an OWA method. Consequently, OWA is considered to be a general and adequate method of performing this kind of evaluation.
4. CONCLUSIONS
The combination of methods for decision making and especially the MCE methods with GIS offer unique capacities for the management and analysis of a great range of spatially-referenced data.
The OWA and WLC methods offer the possibility of integrating and analyzing information from different sources, becoming primary tools for evaluation and decision- making.
According to the research developed at Universidad del Valle, the neutral evaluation of the OWA method was found equivalent to the evaluation by the WLC method, which allow to verify the relation between both methods.
5. ACKNOWLEDGEMENTS
This work was possible thanks to financial assistance from Universidad del Valle with the Universal Accessibility in the Universidad del Valle Approach Plan.
REFERENCES
[1] Zadeh, L. A. Fuzzy Sets. Information and Control 8(3); 338-353. 1965. [ Links ]
[2] Gómez M. & Barredo J. I. Sistemas de información geográfica y evaluación multicriterio en la ordenación del territorio. RaMa. Madrid, 2005. [ Links ]
[3] Malczewski, J. GIS and Multicriteria Decision Analysis. John Wiley & Sons. New York, 1999. [ Links ]
[4] Eastman, J. R. IDRISI 32, Release 2: Guide to GIS and Image Processing, Volume 2. Clark University. Worcester, 2001. [ Links ]
[5] SHANNON, C. E. A mathematical theory of communication. The Bell System Technical Journal. Vol. 27. pp. 379-423, 623-656. 1948. (Disponible en http://cm.bell-labs.com/cm/ms/what/shannonday/shannon1948.pdf; fecha de consulta 10 de marzo de 2010). [ Links ]
[6] Yager, R. R. On Ordered Weighted Averaging Aggregation Operators in Multicriteria Decisionmaking. IEEE Transactions on Systems, Man and Cybernetics 18(1); 183-190. 1988. [ Links ]
[7] Marichal, J. L. Aggregation Operators for Multicriteria Decision Aid [PhD Thesis]. Universite de Liège. Liège. Bélgica. 1999. [ Links ]
[8] Rinner, C., Malczewski, J. Web-enabled spatial decision analysis using Ordered Weighted Averaging (OWA). Journal of Geographical Systems. Springer-Verlag 4; 385-406. 2002. [ Links ]
[9] Rodrigues, D. S. Avaliação Multicritério de Acessibilidade em Ambiente SIG [Tesis de Maestría]. Universidad de Minho. Braga. Portugal, 2001. [ Links ]














