Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
DYNA
versión impresa ISSN 0012-7353versión On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.168 Medellín oct./dic. 2011
CONFINEMENT EFFECTS ON MIXED STATE IN SUPERCONDUCTING PRISMS
EFECTOS DE CONFINAMIENTO SOBRE EL ESTADO MIXTO EN PRISMAS SUPERCONDUCTORES
JOSE JOSE BARBA ORTEGA
Departamento de Física, Universidad Nacional de Colombia, Bogotá - Colombia. jjbarbao@unal.edu.co
Received for review February 24th, 2010; accepted October 25th, 2010; final version November 8th, 2010
ABSTRACT: In this article, we theoretically investigated the vortex configuration of mesoscopic samples of different geometries, imbedded in an external magnetic field. We use the Ginzburg-Landau theory to obtain the spatial distribution of the superconducting electron density in long prisms with a square and triangular cross-section. Taking into account de Gennes boundary conditions via the extrapolation length, b, we study the properties of a mesoscopic superconducting square surrounded by different materials (metallic and another superconductor at higher critical temperature) in the presence of an external magnetic field applied perpendicularly to the square surface. The b-limit for the occurrence of a single vortex in the sample of area d2 is determined. Also, we obtain the vortex configurations for a mesoscopic triangle with the magnetic field applied perpendicularly to a sample plane. In most of the configurations, the vortices present twofold or threefold symmetry.
KEYWORDS: Mesoscopics, Ginzburg-Landau, molecular dynamics, de Gennes parameter
RESUMEN: En el presente trabajo investigamos teóricamente la configuración de vórtices en muestras mesoscópicas de diferentes geometría, inmersas en un campo magnético externo. Usamos la teoría Ginzburg-Landau para obtener la distribución espacial de la densidad de electrones superconductores en un prisma con sección transversal cuadrada y triangular. Tomando en cuenta las condiciones de frontera de de Gennes vía la longitud de extrapolación b, estudiamos las propiedades de un superconductor cuadrado rodeado por diferentes materiales (metálicos y superconductor a mayor temperatura crítica) en presencia de un campo magnético aplicado perpendicular a la superficie del cuadrado. Determinamos el límite de b de ocurrencia de un solo vórtice en la muestra de área d 2. Además, obtenemos la configuración de vórtices para un triangulo mesoscópico con el campo magnético aplicado perpendicularmente al plano de la muestra. En muchas de las configuraciones los vórtices presentan simetría doble o triple.
PALABRAS CLAVE: Mesoscópico, Ginzburg-Landau, dinámica molecular, parámetro de de Gennes.
1. INTRODUCTION
The advances in nanofabrication technologies in recent years allowed for intensive investigation efforts in nanostructured superconductors, both in the experimental and theoretical fronts. It is well know that, for very confined geometries, the superconducting normal magnetic field transition is increased extraordinarily. It was experimentally observed that for an aluminum square and very thin film with the size of a few micrometers, the upper critical field HC2(T) can be increased up to 3.32 times with the inclusion of defects, which is 2.01 times larger than the usual value of HC2(T) [1,2]. Another important issue in confined geometries is the occurrence of giant vortices. The experimental observation of a giant vortex in a mesoscopic superconductor is still a controversial issue. Through multi-small-tunnel-junction measurements in a aluminum thin disk film, Kanda et al [3] developed the multiple-small-tunnel-junction method to distinguish between multivortex and giant vortex states in mesoscopic superconductors, arguing that, as the vorticity increased, giant vortex configuration will occur. Also, scanning SQUID microscopy on Nb thin film, both square and triangle, cannot guarantee giant vortex configurations, at least for low vorticity [4]. On the other hand, applications of superconducting materials necessarily require controlling the density and/or the movement of vortices.
Today it is possible to work out important advances towards vortex manipulation. Strong enhancement of critical properties, such as critical current and field, and highly controllable flux-quanta manipulation have been achieved by reducing the sample size to the mesoscopic scale. Another way of enhancing or changing the properties of superconducting samples can be realized by controlling the sample boundary conditions or introducing into the sample mesoscopic features, such as antidots and insulate, metallic or magnetic dots [5-9]. Theoretically, one can simulate different types of materials by varying the boundary conditions for the order parameter via de Gennes extrapolation length b.
In this article, we present the properties of both mesoscopic superconducting square and triangle prisms in the presence of an external applied magnetic field. This article is organized as follows. Section II presents the numerical method used to solve the time dependent Ginzburg-Landau equations and how to find the vortex configurations and their energies in mesoscopic squares and triangles [10-12]. The discussion of the results is presented in Section III. We present results concerning the vortex state in long mesoscopic superconductors with a square and triangular cross-section. Also, we discuss meta-stable configurations for given values of total vorticity. It is possible that these configurations and their occurrence frequencies can be observed experimentally due to surface barriers. Finally, we present our conclusions in Section IV.
2. THEORETICAL FORMALISM
2.1 Ginzburg-Landau Equations
The time-dependent Ginzburg-Landau equations (TDGL) [13] which govern the superconductivity order parameter Ψ and the vector potential A in the zero electric potential gauge are given by:
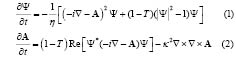
Equations (1) and (2) were rescaled as follows: Ψ in units of 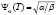 , with α and β being two phenomenological parameters. Lengths in units of length penetration
, with α and β being two phenomenological parameters. Lengths in units of length penetration , time in units
, time in units 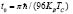 , A in units of
, A in units of 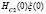 , temperatures T in units of critical temperature
, temperatures T in units of critical temperature 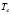 .
.
2.1.1 Boundary Conditions
The dynamical equations are complemented with the appropriate boundary conditions for the order parameter. The general boundary condition for superconductors, found by de Gennes [14], is given by:
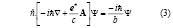
where 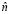 is the unity vector perpendicular to the surface of the superconductor.
is the unity vector perpendicular to the surface of the superconductor. 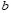 is a real number determining the boundary conditions: a superconductor/vacuum interface is realized for
is a real number determining the boundary conditions: a superconductor/vacuum interface is realized for 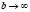 , which means that no superconducting currents can flow out of the superconductor;
, which means that no superconducting currents can flow out of the superconductor; 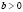 describes a superconductor/metal interface, which will cause superconductivity to be weaker at the edge of the sample (suppressed surface superconductivity);
describes a superconductor/metal interface, which will cause superconductivity to be weaker at the edge of the sample (suppressed surface superconductivity); 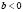 enhances superconductivity because it simulates the presence of a material with higher
enhances superconductivity because it simulates the presence of a material with higher 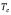 in contact with the superconducting sample; the case of
in contact with the superconducting sample; the case of 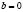 is found for a superconductor/ferromagnet interface or superconducting surfaces with a high density of defects.
is found for a superconductor/ferromagnet interface or superconducting surfaces with a high density of defects.
2.1.2. Numerical Method
The full discretization of the TDGL equations can be found in more detail in Ref. [15]. We use the 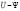 method [16] to solve the TDGL equations in a discrete grid. Complex link variables
method [16] to solve the TDGL equations in a discrete grid. Complex link variables 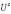 and
and 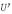 are introduced to preserve the gauge-invariant properties of the discretized equations.
are introduced to preserve the gauge-invariant properties of the discretized equations. 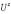 and
and 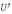 are related to A by:
are related to A by:
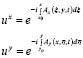 (4)
(4)
The link variable method is used since a better numerical convergence is obtained at high magnetic fields [16]. The TDGL equations (1,2) can be written in the following form:
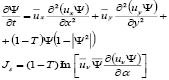 (5)
(5)
where υ = (x,y) and Im indicates the imaginary part. We used this method to obtain our results. The outline of this simulation procedure is as follows: the sample is divided in a rectangular mesh consisting of NxxNy cells, with mesh spacing axxay. To derive the discrete equations, let us define by xi = (i-1)ax, yi = (i-1)ay, an arbitrary vertex point in the mesh and:
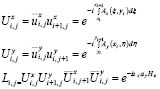 (6)
(6)
Then the discretized version of the TDGL equations maintaining second order accuracy in space is given by:
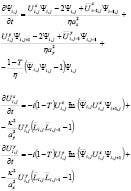 (7)
(7)
The open boundary conditions are:
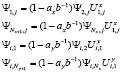 (8)
(8)
In our simulation we use the well know Euler method with 108 time steps of size 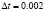 and grid spacing
and grid spacing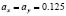 . Ha is the magnetic external field and is increased linearly with the time from 0 to 1, with small intervals of
. Ha is the magnetic external field and is increased linearly with the time from 0 to 1, with small intervals of 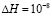 .
. 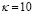 for the square sample and
for the square sample and 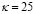 for triangular sample. T = 0.25 for all simulations. The procedure begins at zero applied magnetic field, and the order parameter is initialized as
for triangular sample. T = 0.25 for all simulations. The procedure begins at zero applied magnetic field, and the order parameter is initialized as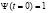 , i.e. the variables are homogeneously initialized to a perfect Meissner state, and A(t=0)=1 (for every point in the domain). The stationary state found for a fixed He is used then as initial condition for the next field value
, i.e. the variables are homogeneously initialized to a perfect Meissner state, and A(t=0)=1 (for every point in the domain). The stationary state found for a fixed He is used then as initial condition for the next field value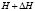 , using a small increments of
, using a small increments of 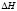 . The applied magnetic field is increased smoothly from zero to a value where the superconductivity will be destroyed completely. For each applied field we follow the temporary evolution of the magnetic induction and of the superconducting order parameter to obtain a stationary solution.
. The applied magnetic field is increased smoothly from zero to a value where the superconductivity will be destroyed completely. For each applied field we follow the temporary evolution of the magnetic induction and of the superconducting order parameter to obtain a stationary solution.
The Ginzburg Landau equations describe the gradient flow for the Gibbs free energy. Thus, in principle, the output of the time dependent Ginzburg Landau should correspond to the global minimum of the energy of the system. The energy, in units of 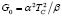 , is given by:
, is given by:
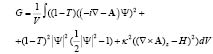 (9)
(9)
The discrete version of this equation is:
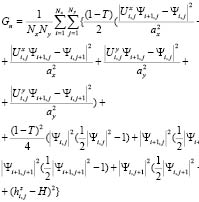 (10)
(10)
3. RESULTS
In this section, we study two mesoscopics systems, a) a mesoscopic superconducting square imbedded by a metallic material or by another superconductor at higher critical temperature and b) a triangular sample surrounded by an insulating material. The resulting |Ψ| for square and triangular configurations with 16 vortices are depicted in Fig. 1. We present the phase diagram in the square size-b parameter plane, for seven square samples with d = 4ξ(0), 5ξ(0), 6ξ(0), 7ξ(0), 8ξ(0), 9ξ(0) and 10ξ (0). We found b = 3.5ξ(0), 0.46ξ(0), 0.055ξ(0), 0.006ξ(0), 0.0008ξ(0), 0.00008ξ(0) and 0.00001ξ(0), respectively in Fig. 2. We can observe a linear behavior of d as a function of lnb, separating the type I from the type II superconductors. The fitted curve corresponds to 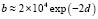 .
.
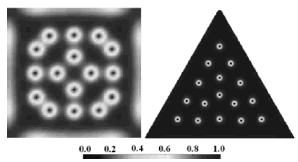
Fig.1. Modulus of the order parameter (|Ψ |) for meta-stable configurations with L=16 at Ha=0.02. Dark and bright regions represent values of the modulus of the order parameter (as well as Δφ⁄2π, from 0 to 1).
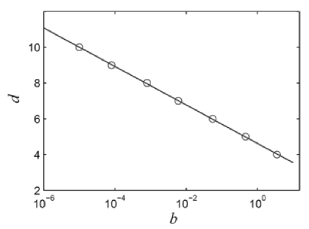
Fig.2. Phase diagram on the square size-b parameter plane.
In Fig. 3 we show the phase diagram in the Ha-1/b plane for a square sample with d = 4?(0). We observe that for 0<1=1/b<0.35, a single quantized vortex enters the sample. For 0.35<1/b<0.42, the transition between the Meissner and the mixed state occurs with the entrance of two single quantized vortices. Finally, for 1/b>0.42, the sample behaves as a Type I superconductor with no vortex state observed. Furthermore, for samples with d<4?(0), we do not observe vortex formation for any magnetic field or b value due to the size restriction of the sample. The above results seem to be in reasonable agreement with previous studies [6]. Also, we study a superconducting square imbedded by another superconductor at higher critical temperature. We use (a) b = -5.0?(0), (b) b = -1.0?(0), (c) b = -0.895?(0), (d) b = -0.8935?(0), (e) b = -0.893?(0) and (f) b = -0.88?(0).
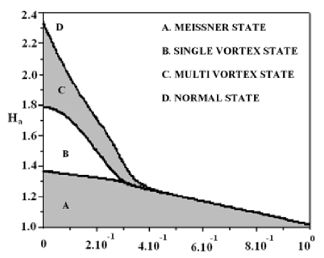
Fig.3. Phase diagram Ha-b-for d=4ξ(0).
The magnetization curve as a function of b is shown in Fig. 4. We can observe a linear behavior of M(b) in the interval [-0.01,-0.06], with m = -0.02±0.0001 as the slope. For this b interval, the sample always remains in the Meissner state and will be more pronounced for smaller values of |b|.
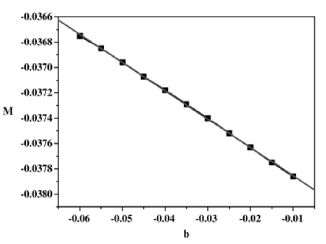
Fig.4. Magnetization as a function of b for a square sample imbedded by another superconductor at a higher critical temperature.
The superconductor electrons density as a function of b is shown in Fig. 5. We observed a power law behavior in the interval [-0.01,-0.06] and obtained a slope of m = -3.32±0.03. For superconductor-superconductor interfaces, the surface barrier is enhanced, resulting in a stronger compression of the vortices in the square. However, if the d-size is dx=5?(0), no vortices are possible in the sample. For dx>5?(0), vortices appear. The limit of the occurrence of a single vortex state is represented in the 5?(0)x5?(0) sample for an applied field of 0.42Hc2. Furthermore, for samples with dx<5?(0) thickness, no vortex can be formed for any magnetic field due to the size restriction.
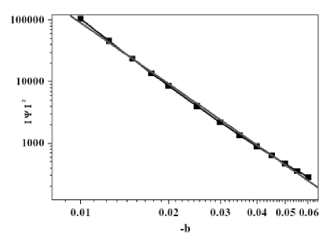
Fig.5. Superconductor electrons density as a function of b.
We studied an equilateral triangle of a=15ξ(0) side length. We obtained the stable and meta-stable vortex configurations for L ranging from 0 to 37 vortices, at different magnetic fields. Giant vortices can also be considered, but the states with lower energy are formed only by singly-quantized vortices [17].
Figure 6 depicts the streamlines of the ground state configurations for L from 1 to 10. The corresponding magnetic field is also plotted on the top or bottom of each figure. The ground state vortex configurations for the triangular numbers L=1, L=3, L=6, L=15, L=28, and L=36, have the Abrikosov lattice-like vortex arrangement together with both three-fold axial and middle plane reflection symmetries. Therefore, these configurations satisfy both the vortex-vortex repulsion and confinement geometry. On the other hand, the ground state configurations with L=2, L=5, L=7, L=9, depicted in Fig. 6, for example, have only middle plane reflection symmetry. In such cases it is preferable to form a vortex molecule configuration, with part of it made of a stable configuration with lower total vorticity and the rest of the vortices distributed along the triangle side.
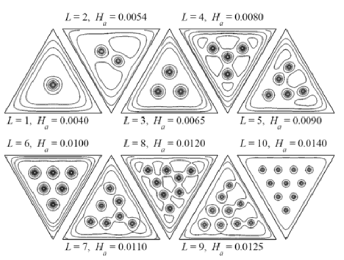
Fig. 6. Streamlines of the ground states vortex configurations for L, from 1 to 10. The total vorticity and the corresponding magnetic field are depicted at the top or the bottom of each figure.
In Fig. 7 we present the meta-stable configurations obtained for L=7 at Ha=0.0150 (Fig. 7(a)), L=19 at Ha=0.0215 (Fig. 7(b)), L=24 at Ha=0.0255 (Fig. 7(c)). For L=7, L=9, and L=24, the configurations with the lowest energy [depicted at the left of Figs. 7(a), 7(b), and 7(c)] posses only middle plane reflection symmetry. Also, these configurations appear more frequently than other meta-stable ones. For L=7 and L=9 the other meta-stable configurations have both middle plane reflection and threefold axial rotation symmetries. Meanwhile, for L=24 one meta-stable configuration has middle plane reflection symmetry and the other one has both symmetries.
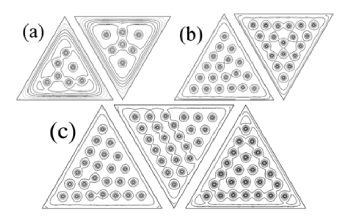
Fig. 7. Current streamlines of the meta-stable vortex configurations (a) L=7 for Ha=0.0150, (b) L=19 for Ha=0.0215, (c) L=24 for Ha =0.0255.
4. CONCLUSIONS
For a superconducting square embedded by a metallic material, we determine the limit of the occurrence of a single vortex state as a function of the de Gennes boundary condition. We observe a linear behavior of lnb as a function of square size. For a superconducting square embedded by another superconductor at higher critical temperature, we found a linear behavior for the magnetization and a power law for the Cooper pair density with the de Gennes parameter. For a superconducting equilateral triangle, we obtained the vortex configurations for different meta-stable states for given values of L and Ha. To increase the probability of finding the lowest energy states, we performed a large number of attempts. Moreover, we also studied the meta-stable configurations, observing that they usually occur less frequently than the lowest energy configuration obtained at the same conditions.
REFERENCIAS
[1] G. R. Berdiyorov, B. J. Baelus, M. V. Milosevic, F.M. Peeters. Stability and transition between vortex configurations in square mesoscopic samples with antidots. Phys. Rev. B 68, 174521. New York. American Physics Society. 2003. [ Links ]
[2] V. V. Moshchalkov. In Connectivity and Superconductivity, edit by J. Berger and J. Rubinstein Springer, Heidelberg, 2000. [ Links ]
[3] A. Kanda, B. J. Baelus, F. M. Peeters, K. Kadowaki, Y. Ootuka. Experimental Evidence for Giant Vortex States in a Mesoscopic Superconducting Disk. Phys. Rev. Letter 93, 257002. New York. American Physics Society. 2004. [ Links ]
[4] T. Nishiro, S. Okayasu, J. Suzuki, K. Kadowaki. Penetration of vortices into micro-superconductors observed with a scanning SQUID microscope, Physica C 412-414, 379. Holland. Elsevier. 2004. [ Links ]
[5] B.J. Baelus, S.V. Yampolskii, F.M. Peeters. Superconducting properties of mesoscopic cylinders with enhanced surface superconductivity. Phys. Rev. B 65, 024510. New York. American Physics Society. 2001. [ Links ]
[6] W. V. Pogosov. Vortex phases in mesoscopic cylinders with suppressed surface superconductivity. Phys. Rev. B 65, 224511. New York. American Physics Society. 2004. [ Links ]
[7] J.J. Barba, L.R.E Cabral, J. Aguiar. Vortex arrays in superconducting cylinders, Physica C 460-462, 1272. Holland. Elsevier. 2007. [ Links ]
[8] J.J. Barba, C.C. de Souza Silva, L.R.E. Cabral, J. Aguiar. Flux trapping and paramagnetic effects in superconducting thin films: The role of de Gennes boundary conditions. Physica C 468, 718. Holland. Elsevier. 2008. [ Links ]
[9] J. Barba, A. Becerra, J. Albino Aguiar. Two dimensional vortex structures in a superconductor slab at low temperatures. Physica C 470, 225, Holland. Elsevier, 2010. [ Links ]
[10] V.R. Misko, V.M. Fomin, J.T. Devreese, V.V. Moshchalkov. Stable Vortex-Antivortex Molecules in Mesoscopic Superconducting Triangles. Phys. Rev. Lett. 90, 147003. New York. American Physics Society. 2003. [ Links ]
[11] G. R. Berdiyorov, L. R. E. Cabral, and F. M. Peeters. Surface barrier for flux entry and exit in mesoscopic superconducting systems. J. Math. Phys. 46, 095105. American Institute of Physics, New York. 2005. [ Links ]
[12] J. Barba, A. Becerra, J. González. Effect of a columnar defect on vortex configuration in a superconducting mesoscopic sample. Braz. J. Phys. 39, 3, 673. Sao Paulo. 2009. [ Links ]
[13] M. Tinkham. Introduction to Superconductivity. McGraw-Hill, New York, 1975. [ Links ]
[14] P.G. de Gennes. Superconductivity of Metals and Alloys, Benjamin, New York, 1966. [ Links ]
[15] D. Gropp, H.G. Kaper, G.K. Leaf, D.M. Levine, M. Palumbo, V.M. Vinokur. Numerical Simulation of Vortex Dynamics in Type-II Superconductors. J. Comput. Phys. 123 (254) Holland. Elsevier. 1996. [ Links ]
[16] G.C. Buscaglia, C. Bolech, A. López. Connectivity and Superconductivity, in: J. Berger, J. Rubinstein (Eds.), Springer, 2000. [ Links ]
[17] L.R.E. Cabral and J. Albino Aguiar. Vortex configurations in thin superconducting equilateral triangles. Phys. Rev. B. 80, 214533. American Institute of Physics, New York. 2009. [ Links ]














