Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas v.78 n.169 Medellín out. 2011
DISEÑO DE UN PLAN DE MUESTREO SIMPLE POR ATRIBUTOS EN BUSCA DE UN OPTIMO SOCIAL
DESIGN OF A SINGLE SAMPLING ATTRIBUTES IN SEARCH OF A SOCIAL OPTIMUM
JOHN HENRY RIOS GRIEGO
MSc., Pontificia Universidad Católica de Chile, jrios@ing.puc.cl.
Recibido para revisar Julio 11 de 2011, aceptado Agosto 19 de 2011, versión final Agosto 31 de 2011
RESUMEN: Los planes de muestreo simple son una de las herramientas empleada en la industria para aceptar o rechazar lotes. Normalmente, los parámetros necesarios -riesgo del productor y riesgo del consumidor, y nivel aceptable de calidad y el nivel límite de calidad- son asignados por cada uno productor o consumidor buscando su beneficio personal. Tomar decisiones en esta forma no tiene en cuenta el daño que un producto no-conforme genera a la sociedad, por ejemplo el daño producido por una maquina defectuosa al operador. En el presente estudio desarrollamos un modelo que combina planes de muestreo simple por atributo con la carta de control del número de productos no-conformes. El modelo maximiza el bienestar social encontrando políticas óptimas de precio, tamaño de muestra y número de aceptación. Esta metodología permite identificar cambios inesperados en el proceso de producción e implementar planes de recuperación de clientes afectados por adquirir productos no-conformes. Finalmente, nuestra metodología también permite implementar planes de mejora continua.
PALABRAS CLAVE: Optimización, Cartas de control, Planes de muestreo simple, Actualización Bayesiana, Programación dinámica.
ABSTRACT: Single sampling plans is one of the tools used in industry for accept or reject lots. Normally, the necessary parameters -producer and consumer’s risk, and acceptable and limiting quality level- are assigned by either producer or consumer seeking their individual benefit. Making decisions in this way does not take into account the damage that a nonconforming product generate to the society, for example the injuries produced by a defective machine to operators. In the present study we develop a model that combines single acceptance sampling plans by attribute with the control chart for number of nonconforming products. The model maximizes social welfare by finding optimal pricing policies, sample size, and acceptance number. This methodology allows identifying unexpected changes in the production process and implementing recovery plans for customer affected by nonconforming products. Finally, our methodology also enhances the implementation of plans for continuous improvement.
KEYWORDS: Optimization, Control charts, Single sampling plans, Bayesian updating, Dynamic programming.
1. INTRODUCCIÓN
En el área de control de calidad, uno de los principales objetivos es hacer las cosas bien desde el comienzo y llevar los procesos a cero defectos [1]. Sin embargo, debido a las fluctuaciones naturales de los procesos y a los costos de producción e inspección, cuando se trata de productos masivos o semimasivos donde se requiere de períodos cortos para obtener una muestra, en la práctica se consigue reducir considerablemente la cantidad de producto defectuoso, existiendo la necesidad de tolerar una pequeña fracción de éste. Para esto Dodge y Roming [2] popularizaron los planes de muestreo para juzgar lotes, donde existen tres alternativas de decisión: (1) aceptar lotes sin inspección; (2) inspeccionar el 100% de los productos y (3) emplear un muestreo de aceptación, y dependiendo de la característica de calidad que se desea evaluar ésta se clasifican por atributos o por variables [3]. Para mayor información sobre planes de muestreo, ventajas y desventajas de éstos remítase a Juran et al. [4], Duncan [5] y Montgomery [6].
Entre los planes de muestreo existente, el de muestreo simple es uno de los más empleados y probados requiriendo inspeccionar sólo una pequeña muestra aleatoria para tomar una decisión sobre aceptar un lote [7]. Este plan se denota por 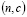 : para un tamaño de muestra
: para un tamaño de muestra 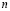 , se rechaza el lote si se encuentran más de
, se rechaza el lote si se encuentran más de 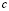 productos no-conformes y este lote rechazado es inspeccionado en su totalidad. Recientemente se ha incrementado el interés por el diseño de planes de este tipo como es el caso de Markowski y Markowski [8], Radhakrishnan y Sankar [9] y Jozani y Mirkamali [3]. En el diseño de planes de muestreo simple, la fracción de producto defectuosa tolerada se define como nivel de calidad aceptable (NCA), con lo cual se espera que exista una probabilidad alta de aceptar un lote y correr un riesgo pequeño de rechazar lotes buenos (riesgo del productor, α). También, es necesario fijar un valor límite de calidad (NLC), donde los lotes que presenten esta fracción de producto defectuoso sean aceptados con una pequeña probabilidad (riesgo del consumidor, β). Es decir, aceptar lotes de mala calidad [10]. Los valores de
productos no-conformes y este lote rechazado es inspeccionado en su totalidad. Recientemente se ha incrementado el interés por el diseño de planes de este tipo como es el caso de Markowski y Markowski [8], Radhakrishnan y Sankar [9] y Jozani y Mirkamali [3]. En el diseño de planes de muestreo simple, la fracción de producto defectuosa tolerada se define como nivel de calidad aceptable (NCA), con lo cual se espera que exista una probabilidad alta de aceptar un lote y correr un riesgo pequeño de rechazar lotes buenos (riesgo del productor, α). También, es necesario fijar un valor límite de calidad (NLC), donde los lotes que presenten esta fracción de producto defectuoso sean aceptados con una pequeña probabilidad (riesgo del consumidor, β). Es decir, aceptar lotes de mala calidad [10]. Los valores de 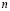 y
y 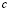 se pueden estimar con base en una distribución hipergeometrica, poisson o binomíal [11], en Schilling [12] se presentan otras distribuciones. Finalmente, inspeccionado el lote y retirado las unidades no-conformes de la muestra, la calidad del lote mejora levemente y la fracción de producto no-conforme remanente recibe el nombre de calidad promedio saliente (CPS).
se pueden estimar con base en una distribución hipergeometrica, poisson o binomíal [11], en Schilling [12] se presentan otras distribuciones. Finalmente, inspeccionado el lote y retirado las unidades no-conformes de la muestra, la calidad del lote mejora levemente y la fracción de producto no-conforme remanente recibe el nombre de calidad promedio saliente (CPS).
Cuando en el proceso de inspección se encuentra un producto con problemas de calidad, los costos y la pérdida de dinero, incluyendo los tiempos de operación se relacionan directamente con el productor, este perjuicio no debe verse sólo de este punto de vista, dado que un producto defectuoso perjudica a la sociedad en general [13].
Los gráficos de control surgen con Shewhart [14] debido a la necesidad de observar las variaciones de los procesos en el tiempo. Estas variaciones se deben a causas naturales propias del proceso o a variaciones atribuibles debido a agentes externos que no pertenecen al proceso [11].
La forma de realizar estos graficos es con base en la relación entre la media 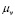 y la desviación estándar
y la desviación estándar 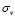 de una característica de calidad
de una característica de calidad 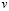 , su límite de control inferior (LCI), la línea central (LC) y el límite de control superior (LCS) vienen dados por:
, su límite de control inferior (LCI), la línea central (LC) y el límite de control superior (LCS) vienen dados por:
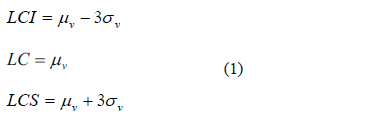
Con lo anterior se asegura que bajo control estadístico debido a fluctuaciones naturales, al seleccionar una muestra 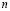 del proceso y graficarla en la carta, existe una probabilidad del 99.73% de que esta se encuentre entre los limites de control [5].
del proceso y graficarla en la carta, existe una probabilidad del 99.73% de que esta se encuentre entre los limites de control [5].
Existen dos tipos de gráficos y estos dependen de la característica de calidad que se quiera medir: para variables, cuando 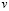 se puede medir por un instrumento de medición y por atributos cuando
se puede medir por un instrumento de medición y por atributos cuando 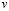 no se pueden medir con un instrumento. Para mayor información referente a gráficos de control, remítase a Juran et al. [4], Duncan [5] y Montgomery [6].
no se pueden medir con un instrumento. Para mayor información referente a gráficos de control, remítase a Juran et al. [4], Duncan [5] y Montgomery [6].
Entre los tipos de gráficos para atributos se tienen la carta del número de no-conformes (CCNN), donde se grafica el número de productos no-conformes encontrados en las muestra  [10].
[10].
La programación dinámica (PD) encuentra la solución óptima de un problema con n variables descomponiéndolo en n etapas, siendo cada etapa un subproblema de una variable y funciona de forma recursiva, dado que la solución óptima de un subproblema se emplea como dato para el siguiente [15]. La recursividad se clasifica en: avance, cuando los cálculos se realizan desde el período inicial hasta el final o de reversas, cuando los cálculos se hacen en sentido contrario [16]. De acuerdo con la información, La PD se clasifica en: 1) problemas determinísticos, cuando la información es conocida, 2) problemas estocásticos, donde la información es desconocida, pero se puede representar por una distribución de probabilidad, y 3) problemas de adquisición de información, donde se tiene incertidumbre y con la información recolectada se estiman las distribuciones [17]. Para mayor información sobre PD remítase a Taha [15], Bertsekas [16] y Powel [17].
La actualización Bayesiana (AB) es un procedimiento iterativo que cumplen con algunos de los supuestos de las cadenas de Markov [18] de primer orden: el conjunto de resultados es finito, la probabilidad en la siguiente etapa sólo depende de las decisiones anteriores. Pero, con la diferencia que las probabilidades de ocurrencia cambian en el tiempo y estas son actualizadas empleando el teorema de Bayes [19].
El teorema de Bayes resuelve el efecto de desestabilización de la probabilidad condicional, donde se sobre estima la importancia de ciertas características de un fenómeno, en dezmero de otras menos evidentes pero igualmente relevantes [20] y viene dado por la expresión:
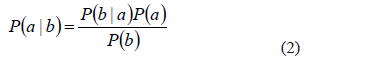
Donde 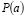 son las probabilidades a priori.
son las probabilidades a priori. 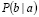 es la probabilidad de b condicionada a
es la probabilidad de b condicionada a 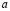 y
y 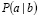 son las probabilidades a posterior.
son las probabilidades a posterior.
Para mayor información sobre AB remítase a Powel [17].
La búsqueda Tabú (BT) es una metaheurística cuya filosofía se basa en la explotación de diversas estrategias inteligentes para la resolución de problemas [21], tuvo sus origines a finales de los 70s cuando fue empleando en problemas lineales de cobertura [22]. Es empleando hoy en día en la teoría de grafos, problemas generales de programación pura y entera mixta y se define como un procedimiento adaptativo empleado para superar las limitaciones de optimalidad local [23]. Para mayor información, aplicaciones y algoritmos de TS remítase a Glover et al. [21], Glover [23] y Glover [24].
En esta investigación proponemos una herramienta que permite diseñar un plan de muestreo simple por atributos (PMSA), cuyo objetivo es maximizar el bienestar fijando políticas óptimas de precios y número de aceptación, disminuyendo la externalidad generada por un producto defectuoso. La metodología propuesta emplea una combinación entre PMSA, CCNN y se basa en el modelo desarrollado por Subrahmanyan y Shoemaker [25]. Pero que al emplear una combinación entre PD de reversa con problemas de adquisición de información y AB lo convierte en un problema hard e irresoluble computacionalmente en la medida que crecen los parámetros, lo anterior se conoce como el problema de dimensionalidad en programación dinámica [15]. Para resolver problemas hard describimos varias metodologías propuestas en la literatura existente y empleadas ampliamente hoy en día.
El resto de este trabajo se organiza de la siguiente forma: En la sección 2, presentamos la descripción, formulación y metodología de solución del problema. En la sección 3, presentamos un caso de estudio donde se ilustra la metodología propuesta. Finalmente, presentamos las conclusiones del artículo y se discuten algunos trabajos futuros que pueden surgir de esta investigación en la sección 4.
2. DESCRIPCIÓN DEL PROBLEMA
A la hora de diseñar planes de muestreo simple, cada uno de los involucrados busca su beneficio personal. Es así, como el proveedor busca α más pequeños, con el fin de que le rechacen menos lotes buenos y el cliente busca menores β, con el objetivo de aceptar menos lotes malos. Obviamente, al proveedor y el cliente también intentaran obtener mayores valores de β y α, respectivamente. Todo esto desde una perspectiva egoísta buscando un beneficio personal y sin tener en cuenta el impacto que causa en la sociedad un producto defectuoso.
Existen otras variables y parámetros involucrados, que las metodologías convencionales no tienen en cuenta a la hora de estimar los parámetros de un plan de muestreo simple, tal es el caso de la fracción de producto defectuoso generada en el proceso productivo, el precio óptimo del producto, el cambio en el bienestar debido a una variación en el número de aceptación, el costo de inspección, el impacto en la sociedad por recibir un producto defectuoso y los costos de recuperación de los clientes por adquirir estos productos.
En esta sección, inicialmente se introduce la notación a utilizar, los supuestos realizados, y algunas consideraciones generales. Luego, se presenta el modelo de actualización Bayesiana. Después, se presenta la formulación del modelo de programación dinámica probabilística que busca un óptimo social. Posteriormente, se presenta la metodología empleada para encontrar los resultados. Entonces, se encuentra el tamaño de la muestra a extraer del lote. Por último, se presenta un mapa conceptual donde se ilustra la metodología.
2.1 Notación, supuestos y consideraciones del modelo
Comenzamos nuestra presentación del modelo mediante la definición de la notación, los supuestos empleados y ciertas consideraciones relevantes.
2.1.1 Notación
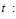 período en que se dividen las entregas.
período en que se dividen las entregas.
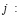 distribución de probabilidad (j=1,2,3).
distribución de probabilidad (j=1,2,3).
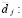 proporción de artículos defectuoso de la distribución
proporción de artículos defectuoso de la distribución 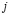 .
.
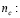 tamaño de muestra para CCNN.
tamaño de muestra para CCNN.
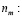 tamaño de muestra para un PMSA.
tamaño de muestra para un PMSA.
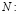 tamaño del lote.
tamaño del lote.
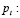 precio por unidad al comienzo del período t.
precio por unidad al comienzo del período t.
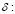 tasa de descuento de flujos.
tasa de descuento de flujos.
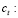 número de aceptación en el período t.
número de aceptación en el período t.
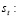 número de artículos no-conformes encontrados en la inspección en el período t.
número de artículos no-conformes encontrados en la inspección en el período t.
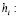 costo por unidad inspeccionada en un PMSA.
costo por unidad inspeccionada en un PMSA.
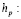 costo de producción por unidad.
costo de producción por unidad.
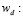 penalización por unidad del producto defectuoso después de la inspección.
penalización por unidad del producto defectuoso después de la inspección.
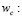 penalización por cada unidad en que se incrementa el número de aceptación debido al cambio en PMSA en un período.
penalización por cada unidad en que se incrementa el número de aceptación debido al cambio en PMSA en un período.
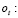 cambio del número de aceptación en un período intermedio
cambio del número de aceptación en un período intermedio 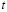 debido a un cambio de plan de muestreo.
debido a un cambio de plan de muestreo.
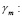 NCA en fracción.
NCA en fracción.
2.1.2 Supuestos
- El proceso de producción se encuentra bajo control estadístico. Además, la empresa supone dos distribuciones adicionales que podrían representar el comportamiento futuro del proceso debido a un cambio no esperado. Cada una de las tres distribuciones tienen una probabilidad de ocurrencia
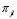 . Dicha probabilidad se irá actualizando a medida que avanza el tiempo en función del comportamiento del proceso.
. Dicha probabilidad se irá actualizando a medida que avanza el tiempo en función del comportamiento del proceso. - Las tres distribuciones de probabilidad se denotan como
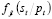 , para un escenario que representa el proceso bajo control estadístico
, para un escenario que representa el proceso bajo control estadístico 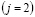 , otro que representa el proceso fuera de control por un incremento en la cantidad de no-conformes
, otro que representa el proceso fuera de control por un incremento en la cantidad de no-conformes 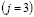 y el último representa una reducción del número de no-conformes (mejora del proceso,
y el último representa una reducción del número de no-conformes (mejora del proceso,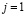 ).
). - La media de cada distribución de precios futuros es decreciente en la medida que mejora la calidad del producto. En otras palabras, entre menor sea la cantidad de producto no-conforme del proceso el precio puede disminuir, debido a la reducción de los reprocesos y las inspecciones.
- El horizonte del estudio se divide en
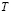 períodos. Estos períodos corresponden a los tiempos entre despachos y la relación cliente-proveedor permite una libre comunicación entre los costos de los diferentes procesos, tal como lo sugiere la filosofía just-in-time Monden [26] entre otras.
períodos. Estos períodos corresponden a los tiempos entre despachos y la relación cliente-proveedor permite una libre comunicación entre los costos de los diferentes procesos, tal como lo sugiere la filosofía just-in-time Monden [26] entre otras.
2.1.3 Consideraciones
En esta sección presentamos ciertas condiciones que deben tenerse en cuenta para el buen funcionamiento del la metodología propuesta.
- Los ingresos derivados de las diferentes penalizaciones van a un fondo mutuo. Dicho dinero se emplea para implementar planes de mejora de calidad y para el proceso de recuperación de los clientes que se vean afectados por seleccionar un producto defectuoso.
- El precio del producto se fija de acuerdo con un rango previamente establecido entre el productor y consumidor. Este precio varía de acuerdo con el comportamiento del proceso en la medida que mejora o se deteriora la calidad del producto durante el horizonte de planificación.
- La empresa puede cambiar el número de aceptación
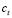 en la medida que se realizan los despachos. Este cambio se realiza antes de cada despacho.
en la medida que se realizan los despachos. Este cambio se realiza antes de cada despacho. - La actualización de
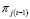 a
a 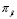 depende de
depende de 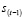 ,
, 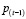 y
y 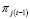 observadas. De esta manera si en el primer período se observa un número de aceptación alto, la probabilidad de que el proceso se encuentre fuera de control aumenta y que sea cualquiera de los dos restantes disminuye. Como
observadas. De esta manera si en el primer período se observa un número de aceptación alto, la probabilidad de que el proceso se encuentre fuera de control aumenta y que sea cualquiera de los dos restantes disminuye. Como 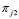 depende de lo que pasó en el período 1 y
depende de lo que pasó en el período 1 y 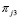 depende de lo sucedido en el período 2 más
depende de lo sucedido en el período 2 más 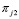 , se tiene que
, se tiene que 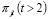 obedece a todo el historial. Esto es que
obedece a todo el historial. Esto es que 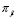 depende de:
depende de: 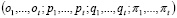 . Dicho historial se denota por la matriz
. Dicho historial se denota por la matriz 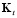 .
. - La razón de operación para un plan de muestreo simple (carta Decameron) se define como razón entre las fracciones del NLC y el NCA en otras palabras cuantas veces cabe el NCA en el NLC y la estimamos con la siguiente ecuación:
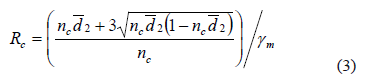
Donde 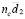 representa la línea central
representa la línea central 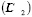 y
y 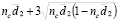 el
el 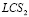 de la CCNN e igual a la fracción del NLC en un PMSA.
de la CCNN e igual a la fracción del NLC en un PMSA.
2.2 Actualización Bayesiana
Para la actualización bayesiana de la probabilidad de ocurrencia, nos basamos en la metodología sugerida por Subrahmanyan y Shoemaker [25], donde proponemos que la función 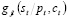 representa la probabilidad de observar un número de no-conformes
representa la probabilidad de observar un número de no-conformes 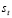 , condicionada a un precio
, condicionada a un precio 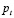 y un número de aceptación
y un número de aceptación 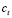 de acuerdo con la distribución de demanda
de acuerdo con la distribución de demanda 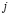 de la siguiente manera:
de la siguiente manera:
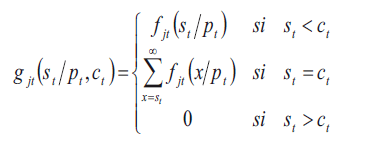
de acuerdo con la probabilidad 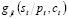 se obtiene la distribución de probabilidades del número de productos no-conformes
se obtiene la distribución de probabilidades del número de productos no-conformes 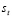 condicionadas
condicionadas 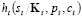 . Para esto se necesitan la probabilidad de ocurrencia de cada demanda
. Para esto se necesitan la probabilidad de ocurrencia de cada demanda 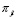 .
.
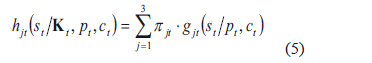
Esta es la probabilidad de una venta, dado un historial 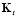 ,
, 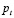 y
y 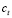 para cada período, luego de observa la cantidad de producto no conforme, se actualizan la probabilidad de ocurrencia, asumiendo que el número de producto no-conforme es real en cada una de las probabilidades de ocurrencia
para cada período, luego de observa la cantidad de producto no conforme, se actualizan la probabilidad de ocurrencia, asumiendo que el número de producto no-conforme es real en cada una de las probabilidades de ocurrencia 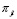 a través de la regla de Bayes. La actualización va cambiando la probabilidad de ocurrencia y se expresa como:
a través de la regla de Bayes. La actualización va cambiando la probabilidad de ocurrencia y se expresa como:
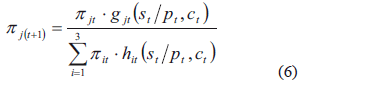
2.3 Formulación
A continuación se plantea un modelo de programación dinámica, el cual pretende maximizar el bienestar, teniendo como variables de decisión el precio y el número de aceptación. El modelo queda expresado de la siguiente manera:
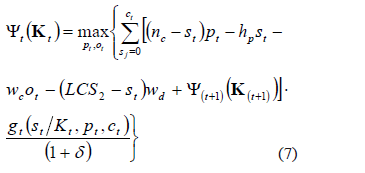
En esencia, este modelo maximiza el bienestar esperado total en el período, teniendo en cuenta los ingresos por la venta del lote, costos de los productos no-conformes encontrados por el plan de muestreo, costos generados por un incremento en el número de aceptación derivados por un cambio de plan en un período intermedio y costos generados por la cantidad de productos no-conformes dentro del lote después de la inspección, más el bienestar esperado dadas las decisiones óptimas en los períodos futuros. En el último período, no se considera el término del bienestar a futuro.
Para resolver este modelo. Primero, estimamos las probabilidades condicionales y posteriormente se utiliza el policy iteration algorithm [27], encontrando el bienestar en el período y obteniendo los valores óptimos en los períodos anteriores 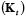 .
.
Dependiendo del estado del proceso, las ecuación 7 queda sujeta a la restricción de número de no-conformes.

Donde 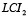 corresponde al límite inferior cuando el proceso se encuentra bajo control y
corresponde al límite inferior cuando el proceso se encuentra bajo control y 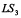 el límite superior cuando se he incrementado la cantidad de producto no-conformes, y son iguales a:
el límite superior cuando se he incrementado la cantidad de producto no-conformes, y son iguales a:
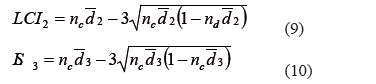
Por último para encontrar el beneficio esperado del productor después de la inspección, a los ingresos por lote se le resta el costo de inspección y de elaboración del producto.
![]()
2.4 Método de solución
Rios et al. [28] encontraron que este tipo de problemas se pueden resolver por métodos exactos siempre y cuando se cumpla con la siguiente ecuación.
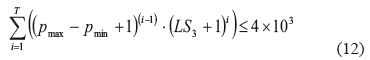
Sin embargo, para problemas de mayor tamaño Rockafellar y Wets [29] proponen hacer un análisis de escenarios en donde el problema de optimización se divide en subproblemas, para cada subproblema se encuentra una solución óptima, para luego encontrar una solución al problema de fondo. Otros autores emplean la programación dinámica aproximada [30]. Esta metodología fue introducida por Werbos [31] que inicialmente la llamó diseños críticos de adaptación (ACDs). También es conocida como programación dinámica heurística [32], ésta herramienta básicamente consiste en resolver dos problemas: El primero, es seleccionar aleatoriamente una muestra que pertenezca al conjunto de soluciones posibles. La segunda, es encontrar un criterio para tomar decisiones. Para luego realizar simulaciones [17]. Otra metodología que permite solucionar este tipo de problemas y empleada por nosotros en esta investigación, es la desarrollada por Rios et al. [28] que consiste en inspeccionar rutas dentro del conjunto de soluciones posibles hasta encontrar la mejor solución. Para esto emplea un algoritmo de búsqueda Tabú.
2.5 Tamaño de muestra PMSA
Para determinar el tamaño de la muestra 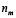 del plan de muestreo simple, empleamos el método Decameron [10] y los pasos para esta metodología son:
del plan de muestreo simple, empleamos el método Decameron [10] y los pasos para esta metodología son:
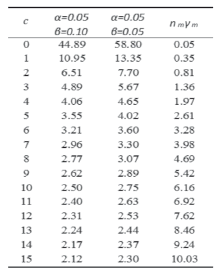
Paso1: Encontrar 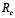 en la Tabla 1 teniendo en cuenta α y β acordados previamente, y el valor de c₀ encontrado.
en la Tabla 1 teniendo en cuenta α y β acordados previamente, y el valor de c₀ encontrado.
Tabla 1: Razón de operación método de Cameron (Fuente: [10]).
Paso2: Emplear la ecuación 3 para estimar 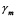 , con el
, con el 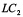 que arroja el proceso y
que arroja el proceso y 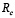 .
.
Paso3: Encontrar 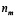 , con el
, con el 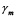 encontrado en el Paso2 y los valores de
encontrado en el Paso2 y los valores de 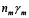 dados en la Tabla 1.
dados en la Tabla 1.
Nota: para poder emplear la tabla de Decameron, el tamaño de la muestra debe ser al menos diez veces menor que el tamaño del lote.
2.6 Diagrama
Una vez conocidos los componentes del plan de muestreo propuesto, en la Figura 1 presentamos un esquema del plan, donde se aprecian los flujos de producto, dinero e inspección.
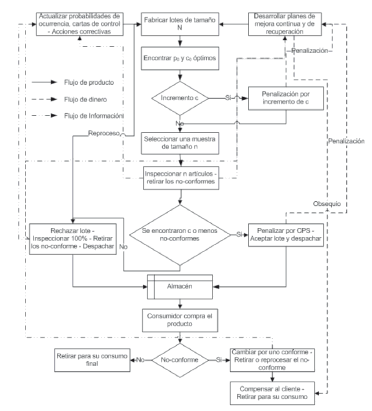
Figura 1. Esquema del plan propuesto
3. CASO DE ESTUDIO
Un caso de estudio empírico fue llevado a cabo con objeto de ilustrar la metodología sugerida. Las condiciones y características del experimento son:
- El estudio consta de dos períodos. En otras palabras solo se hacen dos despachos en el horizonte de planificación.
- El tamaño del lote es de 1,000 unidades. El costo por cada unidad producida es de $10. El costo por inspeccionar una unidad es de $1. La penalización por cada producto defectuoso después de la inspección es $4. Además, se asume que el número de aceptación puede cambiar en los siguientes períodos y se penaliza con $2 por cada unidad que se incrementa. El precio mínimo del producto es $15, mientras que el máximo es $35.
- En la Tabla 2 se presenta la media y la desviación estándar para cada una de las distribuciones sin la sensibilidad al precio. También, se presentas las probabilidades de ocurrencia iniciales asignadas por el tomador de decisiones a cada distribución.
Tabla 2: Parámetros de las distribuciones.
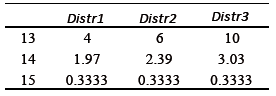
- La media y desviación de los períodos futuros para cada distribución se encuentran con base en las ecuaciones 12.
Donde θ representa la sensibilidad al precio e igual a 0.01 para este ejemplo.
- Se asume un factor de descuento δ igual a 0. El LCS es 8.38% y su fracción es igual al NCL en PMSA. El riesgo del producto es de 0.05 y el del consumidor de 0.10.
El experimento comienza corriendo el algoritmo de búsqueda Tabú desarrollado por Rios et al. [26] con la ecuación 6 y los parámetros mencionados anteriormente. Como resultado se encuentra un precio de venta igual a $34 y el número de aceptación 1 obteniéndose un bienestar esperado de $8,047. Empleando los pasos descritos en la sección 2.4, el tamaño de la muestra es 55 y con la ecuación 9 el beneficio esperado del productor es $23,047.
Para inferir sobre el comportamiento del proceso para el segundo período, si se encontraran 5 productos no-conforme en la muestra. El lote sería rechazado y las probabilidades de ocurrencia para el segundo período serían 0.1101, 0.3116, y 0.5782 para π1 2, π2 2 y π3 2, respectivamente. Lo anterior indica un aumento en la Distr3 mientras que las otras dos disminuyeron. Esto puede indicar que ha aumentado la cantidad de producto no-conforme en el proceso.
Por otro lado, el costo de los productos no-conformes encontrados en la muestra sería de $50, la penalización debida a un incremento en el número de aceptación sería de $8 y la debida a la CPS de $9. Con esto se tendría un fondo de $17 para implementar planes de mejoras antes de iniciar el segundo período.
4. CONCLUSIONES
En esta investigación proporcionamos una herramienta que permite diseñar planes de muestreo simple por atributos, cuando se trabaja con productos masivos o semimasivos, en busca de un óptimo social (maximizar el bienestar). Encontramos que nuestra metodología presenta cuatro ventajas relevantes con respecto a la práctica normal. La primera, es que incorpora el daño generado por un producto no-conforme a la sociedad, involucrando penalizaciones que permiten generar recursos para implementar planes de recuperación y con esto mantener la fidelidad de los clientes. Una segunda, es que permite constantemente conocer los costos generados por la cantidad de producto no conforme debido al CPS, con lo cual se estimula la elaboración de planes de mejora continua en busca de su reducción. Una tercera ventaja se debe a que incorpora probabilidades de ocurrencia, con las cuales se puede inferir sobre el comportamiento del proceso al momento de hacer el muestreo (bajo o fuera de control estadístico). La cuarta ventaja se debe a que fija el precio unitario en función de la calidad del producto. Con esto se logran menores precios en la medida que disminuye el número de productos no-conformes, debido a la reducción en los costos de inspección y de reprocesos, mejorando el resultado operacional de los entes involucrados.
De acuerdo con lo anterior, la metodología sugerida obliga: al productor, a implementar planes de mejora continua disminuyendo así la cantidad de producto no-conforme. Al consumidor, a mantener una comunicación constante con el productor sobre la calidad del producto consiguiendo de esta forma mejores precios. A la sociedad, a mantener la fidelidad con el producto, debido a la buena calidad de esté y también, porque crea fondos que permiten desarrollar planes de recuperación cuando un cliente se ve afectado negativamente por un producto no-conforme.
Sería interesante extender esta metodología a múltiples productos y tener en cuenta la presencia de sustitución y complementariedad entre los diferentes lotes. Otra dirección interesante, es la de trabajar con cartas de control multivariadas.
REFERENCIAS
[1] Crosby P., Quality is free: The art of making quality certain, American Library, New York, 1979. [ Links ]
[2] Dodge H. and Roming H., A method of sampling inspection, The Bell System Technical Journal, 8, pp. 613-631, 1929. [ Links ]
[3] Jozani M. and Mirkamali S., Improved attribute acceptance sampling plans based on maxima nomination sampling, Journal of Statistical Planning and Inference, 140, pp. 2448-2460, 2010. [ Links ]
[4] Jura J. and Gryna F., Quality planning and analysis, McGraw-Hill, New York, 1993. [ Links ]
[5] Duncan A., Quality control and industrial statistics, 4th Edition, McGraw-Hill, New York, 1994. [ Links ]
[6] Montgomery D., Introduction to statistical quality control, John Wiley and Sons, Inc., Hoboken, New Jersey, 2005. [ Links ]
[7] Borget I., Laville I., Paci, S. Michiels A., Mercier L., Desmaris R. and Bourget P., Application of an acceptance sampling plan for postproduction quality control of chemotherapeutic batches in and hospital pharmacy, European Journal Pharmaceutics and Biopharmaceutics, 64, pp.92-98, 2006. [ Links ]
[8] Markowski E. and Markowski C., Improve attribute acceptance sampling plans in the presence of misclassification error, European journal of operational research, 139, pp. 501-510, 2002. [ Links ]
[9] Radhakrishnan R. and Sankar S., Single sampling plan for three attribute classes indexed through acceptance quality level, International Journal of Statistics and Management System 4, pp. 150-164, 2009. [ Links ]
[10] Gutierrez H. y De la Vara R., Control estadístico de calidad y seis sigma, Mc Graw Hill, México D.F., 2004. [ Links ]
[11] Sierra E., Control de calidad, 1st Edition, Biblioteca de Gerencia, Universidad de los Andes, Santa Fe de Bogotá, 1974. [ Links ]
[12] Schilling E., Acceptance sampling in quality control, Marcel Dekker, New York, 1982. [ Links ]
[13] Taguchi G., Chowdhury S. and Wu Y., Taguchi´s Quality Engineering, John Wiley & Sons Inc., New Jersey, 2005. [ Links ]
[14] Shewart W., Economic control of quality of the manufactured product, Quality, Van Nostrand, New York, 1931. [ Links ]
[15] Taha H., Investigación de operaciones, Optimización, Ed. Prentice Hall, México, 2004. [ Links ]
[16] Bertsekas D., Dynamic programming and optimal control, Athena Scientific, Belmont, 1995. [ Links ]
[17] Powell W., Approximate dynamic programming: Solving the curses of dimensionality, John Wiley & Sons, Inc., New Jersey, 2007. [ Links ]
[18] Shamblin J. and Stevens G., Operation research a fundamental approach, New York, McGraw-Hill, 1994. [ Links ]
[19] Thomson B., Schatzmann J. and Young S., Bayesian update of dialogue state for robust dialogue systems, 2008 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Nevada, USA, pp. 4937-4940, March 2008. [ Links ]
[20] Singer M., Teoría de juegos para los dilemas estratégicos. Pontificia Universidad Católica de Chile (libro en proceso de elaboración), 2008. [ Links ]
[21] Glover F. y Melián B., Tabu search, Revista Interamericana de Inteligencia Artificial, 19, pp. 29-48, 2003. [ Links ]
[22] Glover F., Heuristic for integer programming using surrogate constraints, Decision Sciences, 8, pp.156-166, 1977. [ Links ]
[23] Glover F. Tabu search part I, ORSA Journal on Computing, 1, pp. 190-206, 1989. [ Links ]
[24] Glover F. Tabu search part II, ORSA Journal on Computing, 1, pp. 190-206, 1990. [ Links ]
[25] Subrahmanyan S. and Shoemaker R., Developing optimal pricing and inventory policies for retailers who face uncertain demand, Journal of Retailing, 72, pp. 7-30, 1996. [ Links ]
[26] Monden Y., Toyota production system: an integrated approach to just-in-time, Production, Engineering & Management Press, Georgia, 1997. [ Links ]
[27] Howard R., Dynamic programming and markov process, MIT Press, Massachusetts, 1960. [ Links ]
[28] Rios J., Ferrer J., Perez M.J. and Grumwald M., Heuristic approach in solving pricing and inventory policies for seasonal products with uncertain demand, Pontificia Universidad Católica de Chile (working paper), Santiago, 2011. [ Links ]
[29] Rockafellar R., Wets R., Scenarios and policy aggregation in optimization under uncertainty, Mathematics of operations research, 16, pp. 119-147, 1991. [ Links ]
[30] Liu D. Approximate dynamic programming for self-learning control, ACTA Automatica Sinica, 31, pp. 13-18, 2005. [ Links ]
[31] Werbos P., Advanced forecasting methods for global crisis warning and models of intelligence, General Systems, 22, pp. 25-38, 1977. [ Links ]
[32] Lendaris G. and PAINTZ C., Training strategies for critic and action neural networks in dual heuristic programming method. Memory in the International Conference on Neural Networks, TX, USA, 2, pp. 712-717, Junio 1997. [ Links ]













