Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas v.78 n.169 Medellín out. 2011
ALGORITMO PARA EL APRENDIZAJE DE REGLAS DE CLASIFICACION BASADO EN LA TEORÍA DE LOS CONJUNTOS APROXIMADOS EXTENDIDA
ALGORITHM TO LEARN CLASIFICATION RULES BASED ON THE EXTENDED ROUGH SET THEORY
Yaima Filiberto
MSc., Universidad de Camagüey, Cuba, yaima.filiberto@reduc.edu.cu
Rafael Bello
Dr., Universidad Central de Las Villas, Cuba, rbellop@uclv.edu.cu
Yailé Caballero
Dra., Universidad de Camagüey, Cuba, yaile.caballero@reduc.edu.cu
Mabel Frías
Ingeniera Informática. Facultad de Informática. Universidad de Camagüey, Cuba, mabel.frias@reduc.edu
Recibido para revisar Marzo 27 de 2011, aceptado julio 27 de 2011, versión final Agosto 3 de 2011
RESUMEN: Los conjuntos aproximados han demostrado ser efectivos para desarrollar técnicas de aprendizaje automático, entre ellos métodos para el descubrimiento de reglas de clasificación. En este trabajo se presenta un algoritmo para generar reglas de clasificación basado en relaciones de similaridad, lo que permite que sea aplicable en casos donde los rasgos tienen dominio discreto o continuo. Los resultados experimentales muestran un desempeño satisfactorio en comparación con otros algoritmos conocidos como C4.5 y MODLEM.
PALABRAS CLAVE: Reglas de clasificación, relaciones de similaridad, Teoría de los conjuntos aproximados, minería de datos
ABSTRACT: Rough sets have allowed developing several machine learning techniques, among them methods to discover rules of classification. In this paper, we present an algorithm to generate rules of classification based on similarity relations, this allows to apply this method in the case of features with discrete or real domains. The experimental results show a satisfactory performance of this algorithm in comparison with other such as C4.5 and MODLEM.
KEYWORDS: Classification rules, similarity relations, Rough set theory.
1. INTRODUCCIÓN
Las reglas de decisión son una de las formas de representación del conocimiento típicas para formalizar el conocimiento descubierto, debido a su expresividad simbólica es considerada más comprensible y natural para los humanos que otros formalismos; además, las reglas constituyen bloques de conocimiento y los expertos del dominio pueden fácilmente analizarlas individualmente [1], [2]. Las reglas representan funciones que establecen una relación entre los ejemplos (descritos mediante un conjunto de rasgos) y las clases de decisión. Se expresan de la forma If P then Q, donde P es la parte condicional formada usualmente por una conjunción de condiciones elementales (p1 and p2 and ... pk), y Q es la parte de decisión que asigna un valor de decisión (clase) a un objeto que cumpla la condición. Las reglas constituyen patrones que establecen una dependencia entre los valores de los atributos de condición en P y el valor de decisión Q. En la mayoría de los métodos de aprendizaje automático para la inducción de reglas la parte P se construye incrementalmente, agregando sucesivamente las condiciones elementales pi hasta que se cumpla una condición dada; los términos pi son pruebas sobre los valores de los atributos (mediante los operadores de igualdad, menor que, mayor que, etc.). La búsqueda de la mejor condición elemental a ser añadida a la conjunción depende de un criterio de evaluación, el cual trata de inducir reglas con el menor número de condiciones y con el mayor cubrimiento posible; por eso la cantidad de alternativas posible es grande.
El aprendizaje de reglas de clasificación es un problema clásico del aprendizaje automático. La mayoría de los métodos tratan de generar reglas siguiendo una estrategia de cubrimiento secuencial. Estos métodos utilizan un conjunto de entrenamiento (o aprendizaje) compuesto por objetos descritos por atributos de condición (con los cuales se forman las condiciones pi) y el rasgo de decisión (clase). La construcción de clasificadores es una de las técnicas usadas comúnmente en minería de datos [3]. Entre los algoritmos clásicos para resolver este problema está el ID3, y su extensión para el caso de rasgos de condición con dominio continúo C4.5 [4], los cuales inducen árboles de decisión. La presencia de rasgos con dominio continuo introduce una complejidad mayor en el proceso de descubrimiento de las reglas. Las alternativas seguidas han sido discretizar los rasgos de dominio continuo previamente al proceso de generación de las reglas o realizar simultáneamente la discretización y la inducción de las reglas [5], como es el caso del algoritmo C4.5 [6], el cual se ha convertido en un estándar entre las técnicas de aprendizaje automático para el descubrimiento de reglas de clasificación; fue considerado entre los 10 algoritmos que más han influido y mayor uso han tenido en la minería de datos [3].
La Teoría de los conjuntos aproximados (Rough set theory, RST) ofrece herramientas útiles para el análisis de datos; entre ellas algoritmos para el descubrimiento de reglas de clasificación (decisión). Entre los más conocidos están LEM2 (Learning from Examples Module v2), un algoritmo que es parte del sistema de minería de datos LERS (Learning from Examples based on Rough Sets) [7-9], y dos algoritmos basados en LEM2, MODLEM [10-12], y MLEM2 [13], los cuales tratan de encontrar un conjunto mínimo de reglas que permitan realizar la clasificación (lo cual significa que los ejemplos del conjunto de aprendizaje son cubiertos por el número mínimo de reglas no redundantes). El algoritmo LEM2, similar a ID3, solo considera condiciones elementales de la forma atributo=valor, por eso en el caso de los rasgos de dominio continuo requiere de una fase de preprocesamiento en el cual se discretizan estos dominios. Los algoritmos MODLEM y MLEM2 son capaces de considerar atributos de dominio continuo pues realizan simultáneamente la discretización y la inducción y generan la parte P de las reglas como conjunciones con una sintaxis más general. El algoritmo MODLEM busca sucesivamente cubrimientos de las aproximaciones de las clases de decisión por conjuntos mínimos de reglas. En [10] se presentó un estudio comparativo entre MODLEM y LEM2 sobre datos numéricos, los resultados mostraron que MODLEM alcanzó resultados con una precisión comparable a la alcanzada por la mejor variante lograda por LEM2 considerando diferentes alternativas de discretización. Los resultados presentados en [14] mostraron que MODLEM alcanza un desempeño similar al algoritmo C4.5. Otros estudios sobre el descubrimiento de reglas de decisión usando conjuntos aproximados se presentan en [11, 15-20].
En este artículo se presenta un método para inducir reglas de clasificación para sistemas de decisión con rasgos de condición heterogéneos, es decir, pueden existir tanto rasgos discretos como continuo. El mismo se distingue de los antes mencionados en que no requiere discretizar los dominios continuos, y la parte condicional de la regla no se expresa como una conjunción de condiciones elementales. El algoritmo se basa en el empleo de una relación de similaridad que permite construir las clases de similaridad de los objetos. La construcción de las relaciones de similaridad se basa en la Teoría de los conjuntos aproximados extendida [21]. Los estudios experimentales desarrollados muestran un mejor desempeño de este algoritmo al compararlo con C4.5 y MODLEM.
2. LA TEORÍA DE LOS CONJUNTOS APROXIMADOS
La Teoría de los Conjuntos Aproximados (Rough Set Theory, RST) fue propuesta por Pawlak en 1982 [22]. Al desarrollar diversas técnicas para el análisis de datos basados en los conjuntos aproximados, la información es representada por una tabla donde cada fila representa un objeto y cada columna representa un rasgo. Esta tabla se denomina Sistema de Información; más formalmente, es un par ![]() , donde U es un conjunto finito no vacío de objetos llamado Universo y A es un conjunto finito no vacío de atributos. Un Sistema de Decisión es cualquier sistema de información de la forma
, donde U es un conjunto finito no vacío de objetos llamado Universo y A es un conjunto finito no vacío de atributos. Un Sistema de Decisión es cualquier sistema de información de la forma 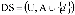 , donde dÏA es el atributo de decisión. Los conceptos básicos de RST son los conceptos de aproximación inferior y superior. Una definición clásica de aproximación inferior y superior fue originalmente introducida con referencia a una relación de inseparabilidad (indiscernibility relation) la cual es una relación de equivalencia.
, donde dÏA es el atributo de decisión. Los conceptos básicos de RST son los conceptos de aproximación inferior y superior. Una definición clásica de aproximación inferior y superior fue originalmente introducida con referencia a una relación de inseparabilidad (indiscernibility relation) la cual es una relación de equivalencia.
Sea 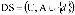 un sistema de decisión y
un sistema de decisión y 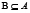 y
y 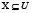 . B define una relación de equivalencia y el subconjunto X es un concepto en el universo U. La relación B se define de la forma siguiente: los objetos (x,y) son inseparables según B si
. B define una relación de equivalencia y el subconjunto X es un concepto en el universo U. La relación B se define de la forma siguiente: los objetos (x,y) son inseparables según B si 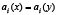 , para todo rasgo i en B, donde ai(x) denota el valor del rasgo i en el objeto x (es decir, dos objetos son inseparables de acuerdo al subconjunto de rasgos B si tienen igual valor para todos los rasgos en B). Un conjunto X se puede aproximar usando sólo la información contenida en B mediante la construcción de la aproximaciones B-inferior y B-superior, denotadas por B*X y B*X respectivamente, y definidas por las expresiones:
, para todo rasgo i en B, donde ai(x) denota el valor del rasgo i en el objeto x (es decir, dos objetos son inseparables de acuerdo al subconjunto de rasgos B si tienen igual valor para todos los rasgos en B). Un conjunto X se puede aproximar usando sólo la información contenida en B mediante la construcción de la aproximaciones B-inferior y B-superior, denotadas por B*X y B*X respectivamente, y definidas por las expresiones:
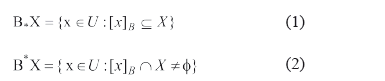
Donde 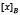 denota la clase de x de acuerdo a la relación de inseparabilidad B. Los objetos en B*X son con certeza miembros de X, mientras los objetos en B*X son posiblemente miembros de X. Un reducto es un conjunto minimal de atributos BÍA tal que
denota la clase de x de acuerdo a la relación de inseparabilidad B. Los objetos en B*X son con certeza miembros de X, mientras los objetos en B*X son posiblemente miembros de X. Un reducto es un conjunto minimal de atributos BÍA tal que 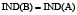 , es decir ambos generan la misma partición del universo U.
, es decir ambos generan la misma partición del universo U.
Cuando el dominio de los rasgos en B no es discreto, una relación de inseparabilidad definida de esta forma no es aplicable. La relación de equivalencia es muy estricta en caso de dominios continuos pues ligeras diferencias entre los valores de los objetos para un rasgo pueden no ser significativas al analizar su inseparabilidad; por ejemplo, una temperatura de 37.8 grados puede ser considerada igual a otra de 37.9 grados, al medir la temperatura corporal de dos personas. Esto es especialmente importante en el caso de rasgos numéricos en los cuales pequeños errores en la medición de los mismos pueden generar estas diferencias. En este caso se tienen dos alternativas, se discretizan los rasgos de dominio continuo o se usan otros tipos de relaciones de inseparabilidad entre los objetos del universo U. Emplear una relación de similaridad en lugar de una relación de equivalencia es más adecuado en estos casos. Remplazando la relación de equivalencia por una relación binaria más débil, se obtiene una extensión del enfoque clásico de la RST. Algunas extensiones se estudian en [23-27].
Esto se logra extendiendo el concepto de inseparabilidad entre objetos de modo que se agrupen en la misma clase los objetos similares, no idénticos, según una relación de similaridad R. Las relaciones de similaridad no inducen una partición del universo U, sino generan clases de semejanza para cualquier objeto 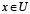 . La clase de semejanza de x, de acuerdo a la relación de similaridad R se denota por R(x) y se define como
. La clase de semejanza de x, de acuerdo a la relación de similaridad R se denota por R(x) y se define como 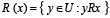 . Esta se lee como “el conjunto de objetos del universo U que son similares al objeto x de acuerdo a la relación R". Un ejemplo es el caso de las relaciones de tolerancia (tolerance relation) [28], donde la relación
. Esta se lee como “el conjunto de objetos del universo U que son similares al objeto x de acuerdo a la relación R". Un ejemplo es el caso de las relaciones de tolerancia (tolerance relation) [28], donde la relación 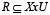 es reflexiva (
es reflexiva (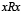 ) para cualquier
) para cualquier 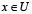 y simétrica (
y simétrica (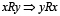 ) para cualquier par
) para cualquier par 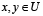 .
.
Mientras que las relaciones de equivalencias inducen una partición del universo, las relaciones de similaridad inducen un cubrimiento del universo. Un cubrimiento del universo U es una familia de subconjuntos no vacíos cuya unión es igual al universo. Una partición de U es un cubrimiento, de modo que el concepto de cubrimiento es una extensión del concepto de partición.
En [29, 30], se propone una medida, denominada calidad de la similaridad, para el caso de sistemas de decisión continuos, esta medida permite construir relaciones de similaridad en la RST extendida, y también calcular pesos para los rasgos en sistemas de decisión continuos; utilizando una meta heurística, en este caso optimización basada en partículas (PSO) [31], se busca el conjunto de pesos para los rasgos que permite maximizar la medida calidad de la similaridad, como se describe la sección 3. Basado en este método de construcción de una relación de similaridad se ha elaborado un algoritmo de descubrimiento de reglas de clasificación (decisión), que se describe en la sección 4.
3. CONSTRUCCION DE LA RELACION DE SIMILARIDAD
El método de construcción de relaciones de similaridad propuesto en [29, 30] parte del principio de que “problemas similares tienen soluciones similares" (vectores de entrada similares tienen valores de salida similares). Es decir, dadas dos relaciones:
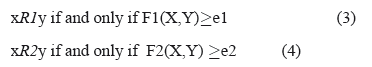
las cuales establecen una relación de similaridad entre dos objetos (x,y) del universo considerando la semejanza de los mismos respecto a los rasgos en A (calculada según la función F1 en la relación R1) y el rasgo objetivo (calculada según la función F2 en relación R2), el propósito es encontrar las relaciones R1 y R2 tal que R1(x) y R2(x) sean lo más parecido posible para cualquier elemento del universo. Basado en este enfoque, se construyen los conjuntos:
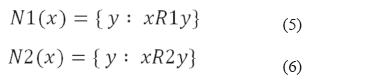
El problema es encontrar las funciones F1 y F2 tal que N1(x)=N2(x), donde el símbolo “=" la mayor similaridad posible entre los conjuntos N1(x) y N2(x) para todo objeto del universo. El grado de similaridad entre ambos conjuntos para un objeto x se expresa por la medida siguiente:
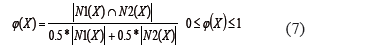
A partir de la cual se define mediante la expresión (8) la medida calidad de la similaridad de un sistema de decisión (DS) con un universo de M objetos:
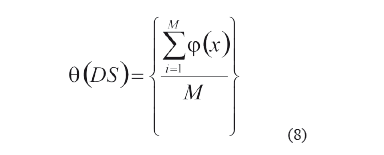
El objetivo es maximizar el valor de la medida q(DS). El valor de esta medida depende de la función F1. Usando la suma pesada definida por la expresión (11), y dadas las funciones de comparación para cada rasgo, el problema se reduce a encontrar el conjunto de pesos W={w1, w2,...,wn}, para lo cual se emplea una meta heurística, como la Optimización basada en partículas (Particle Swarm Optimization, PSO) [31].
4. ALGORITMO PARA GENERAR REGLAS DE CLASIFICACIÓN BASADO EN RELACIONES DE SIMILARIDAD
El algoritmo para la inducción de reglas de clasificación que se presenta en esta sección permite descubrir conocimiento a partir de sistemas de decisión que contienen tanto rasgos con dominio discreto como continuo, pues la diferencia entre ambos tipos de dominios solo radica en la función de comparación de rasgos que se utilice; lo cual hace que no requiera realizar ningún proceso de discretización, ni antes del aprendizaje como ID3 o LEM2 ni durante el aprendizaje como C4.5 o MODLEM. El algoritmo induce reglas de la forma Si P entonces Q, pero en este caso la condición P tiene la forma ∑wi*di()≥ε, donde wi es el peso del rasgo i, di() es la función de comparación para el rasgo i y ε es un umbral. Este algoritmo busca el conjunto mínimo de reglas siguiendo una estrategia de cubrimiento secuencial, para lo cual construye clases de similaridad de los objetos del sistema de decisión. El algoritmo comprende un módulo principal con tres pasos y dos procedimientos para la construcción de las reglas.
Algoritmo IRBASIR (Inducción de reglas basado en relaciones de similaridad)
Dado un sistema de decisión DS=(U, AÈ{d}), con m objetos, y el conjunto A contiene n rasgos de dominios continuos o discretos.
P1. Definir las medidas de similaridad locales.
Construir las funciones de comparación de rasgos di(x,y) para cada rasgo en A, tales que permiten comparar los valores de ese rasgo; por ejemplo la expresión (9).
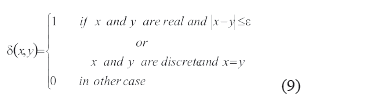
P2. Construir una relación de similaridad R, como la definida por (3):
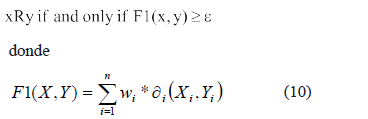
P3. Construir reglas de clasificación según el procedimiento GenRulesRST basado en R.
Activar GenRulesRST.
Para encontrar los valores wi para (10) se propone usar el método propuesto en [1] y [2] descrito en la sección 3. El procedimiento GenRulesRST genera reglas de clasificación y sus correspondientes valores de certidumbre.
Procedimiento GenRulesRST
Se usa un arreglo de m componentes, denominado Usado[], en el cual Usado[i] tiene un valor 1 si el objeto ya fue usado por el procedimiento GenRulesRST, o 0 en otro caso. En este procedimiento se buscan objetos del sistema de decisión no tenidos en cuenta previamente, se construye su clase de similaridad usando la relación de similaridad seleccionada y se construye una regla que cubra los objetos que tienen como valor de decisión la clase mayoritaria en la clase de similaridad.
P1: Inicializar contador de objetos
Usado[j] ← 0, para j=1,...,m
RulSet ← f
i ← 0
P2: Comienza procesamiento del objeto Oi
i ← índice del primer objeto no usado
Si i=0 entonces Fin del proceso de generación de reglas.
Sino Usado[i] ← 1
P3: Construir la clase de similaridad del objeto Oi según R
Calcular [Oi]R [x]R denota la clase de similaridad del objeto x
P4: Generación de una regla de decisión
Si |f([Oi]R)|=1 entonces {/*Construir la regla que describa esta clase de similaridad con consecuente igual al valor de decisión del objeto Oi*/
k ← d(Oi)
C ← [Oi]R}
Sino { /*Construir la regla que describa esta clase de similaridad con consecuente igual al valor de decisión mayoritario en [Oi]R */
k ← valor de decisión mayoritario de los objetos en [Oi]R
C ← objetos de [Oi]R con clase k}
Activar GenRulSim(k, [Oi]R, C; Rul) /* este procedimiento construye una regla de decision*/
RulSet ← RulSet U { Rul }
P5: Marcar como usados a todos los objetos en C cubiertos por la regla Rul y con consecuente k.
P6: Ir a P2
Donde |f([Oi]R)| denota la cantidad de valores de decisión distintos de los objetos en la clase de similaridad [Oi]R.
Procedimiento GenRulSim(k, Cs, C; Rul)
Los parámetros k, Cs y C son de entrada y Rul de salida.
P1: Construir un vector P con n componentes de referencia para el conjunto de objetos en C.
P(i) ← f(Vi), donde Vi es el conjunto de valores del rasgo i en los objetos en C
P2: Generar la regla a partir del vector de referencia P.
Rul ← If w1*d(X1,P1)+...+ wn*d(Xn,Pn) ≥ e then d=k
Donde los pesos wi son tomados de la función F1 (expresión 10); e es el umbral usado en la relación de similaridad R; Pi es el valor del rasgo i en el vector de referencia P; y di es la función de comparación para el rasgo i.
P3: Calcular la certidumbre de la regla.
Considerar las medidas de accuracy (Acc) y coverage (Cov):
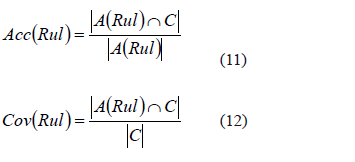
Donde A(Rul) es el conjunto de objetos en Cs para los cuales el antecedente de la regla Rul se cumple.
En paso P1 de GenRulSim la función f denota un operador de agregación; por ejemplo: Si los valores en Vi son reales usar el promedio, si son discretos la moda. El propósito es construir un prototipo o centroide para un conjunto de objetos similares; aquí se ha usado un enfoque parecido a como se hace en el algoritmo k-means [3]; en [32] se presentan diferentes alternativas al respecto.
5. RESULTADOS EXPERIMENTALES
Con el fin de evaluar la precisión del algoritmo fue realizado el siguiente estudio. Se utilizaron 12 bases de datos de la UCI Repository [33] donde la mayoría de los atributos en A tienen dominio continuo y el rasgo d discreto. Para la validación de los resultados se utiliza el proceso de validación cruzada.
El método de validación cruzada, subdivide el conjunto de datos original en k subconjuntos de igual tamaño, uno de los cuales se utiliza como conjunto de prueba mientras los demás forman el conjunto de entrenamiento. Luego la precisión general del clasificador es calculada como el promedio de las precisiones obtenidas con todos los subconjuntos de prueba. Al utilizar esta técnica se tuvo en cuenta la cantidad de subconjuntos con los que se trabajó, porque con mayores valores para K, la tendencia del rango del error real de la estimación se reduce, la estimación será más precisa, la varianza del rango del error real es mayor y el tiempo de cómputo necesario también aumenta ya que aumenta la cantidad de experimentos a realizar. A medida que k se hace más pequeño, el número de experimentos y por consiguiente el tiempo computacional se reducen, la varianza de la estimación se reduce también y la tendencia de la estimación se hará mayor (conservativa o mayor que el rango del error real). Ateniendo a esto se trabajó con el valor típico recomendado k=10. Esta técnica elimina el problema del solapamiento de los conjuntos de prueba y hace un uso efectivo de todos los datos disponibles.
Las bases utilizadas en el estudio se describen en la Tabla 1.
Tabla 1. Descripción de las bases de datos usadas para la experimentación
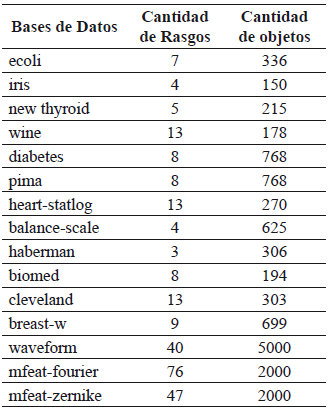
Para la experimentación se compararon los resultados obtenidos con dos versiones del algoritmo C4.5 (los clasificadores C4.5 de la herramienta KEEL[34], y J48 de la herramienta Weka [35]), el algoritmo MODLEM de la herramienta ROSE2 [36] y el algoritmo propuesto (IRBASIR).
Experimento 1: Comparar los resultados de precisión de los clasificadores C4.5, J48, MODLEM e IRBASIR para cada una de las BD, para las diez particiones que se realizaron.
Objetivos: Determinar la precisión de la clasificación de los clasificadores C4.5, J48, MODLEM e IRBASIR para cada una de las BD.
En la Tabla 2 se muestran los resultados de la comparación de los algoritmos.
Tabla 2. Resultados de la precisión de la clasificación de los algoritmos C45, J48, MODLEM e IRBASIR
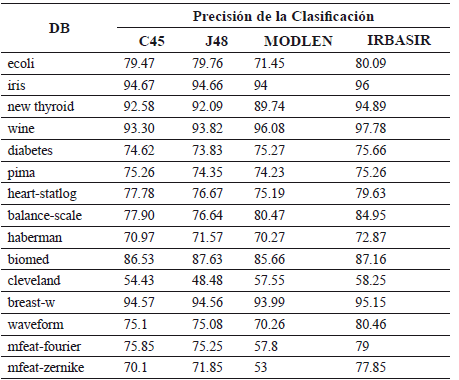
En todos los casos la precisión de la clasificación que se alcanza cuando se usan las reglas inducidas por el algoritmo IRBASIR fue superior a las generadas por los algoritmos C4.5, J48 y MODLEM. Para comparar los resultados se utilizaron test de comparaciones múltiples con el fin de encontrar el mejor algoritmo. En la Tabla 3 se puede observar que el mejor ranking lo tiene el método propuesto IRBASIR.
Tabla 3. Rankings obtenido con el Test de Friedman
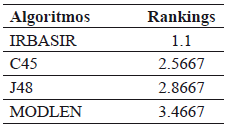
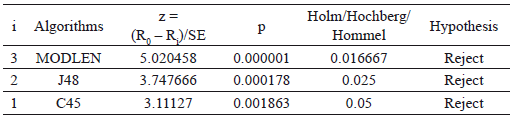
El Test de Iman-Davenport (F-distribution con 3 y 42 grados de libertad) fue empleado con el fin de encontrar diferencias significativas entre los algoritmos IRBASIR, C4.5, J48 y MODLEM, obteniendo mediante el Test de Friedman valor de p-value: 0.000005. De esta forma en la Tabla 4 se muestran los resultados del procedimiento de Holm para comparar el algoritmo propuesto IRBASIR con los restantes. El test rechaza para todos los casos a favor del algoritmo de mejor ranking por lo que se puede observar que algoritmo propuesto es estadísticamente superior a los restantes en cuanto a la precisión de la clasificación.
Tabla 4. Tabla de Holm para α = 0.05, con IRBASIR como método de control.
6. CONCLUSIONES
En este artículo se ha presentado el algoritmo IRBASIR (Inducción de reglas basado en relaciones de similaridad) para la generación de reglas de clasificación, el empleo de relaciones de similaridad permite tratar tanto rasgos con dominio discreto como continuo sin necesidad de discretizar los dominios continuos. La construcción de relaciones de similaridad se basa en la Teoría de los conjuntos aproximados extendida. El algoritmo induce reglas en las cuales la parte condicional de la misma no se expresa como una conjunción de condiciones elementales, como ocurre en la mayoría de los métodos. Al compararse con otros algoritmos conocidos (C4.5, J48 y MODLEM) para descubrir reglas en este tipo de información los resultados muestran un desempeño superior del algoritmo IRBASIR.
REFERENCIAS
[1] Michalski, R.S., A theory and methodology of inductive learning. In: Michalski,. Machine Learning: An Artificial Intelligence Approach, pp. 83-134, 1983. [ Links ]
[2] Stefanowski, J. and Wilk, S., Extending Rule-Based Classifiers to Improve Recognition of Imbalanced Classes. Advances in Data Management SCI, 223, pp. 131-154, 2009. [ Links ]
[3] Xindong, W., Top 10 algorithms in data mining. Knowledge Information System, 14, pp. 1-37, 2008. [ Links ]
[4] Mitchell, T., Machine Learning, Ed. Science/Engineering/Math, Portland, OR, USA: McGraw Hill, 1997, [ Links ]
[5] Grzymala-Busse, J.W., Three Strategies to Rule Induction from Data with Numerical Attributes. Transactions on Rough Sets II, LNCS, 3135, p p. 54-62, 2004. [ Links ]
[6] Quinlan, J.R., C-4.5: Programs for machine learning, ed. M. Kaufmann, San Mateo, California, 1993 [ Links ]
[7] Grzymala-Busse, J.W., LERS- A system for learning from examples based on rough sets. Intelligent Decision Support, Handbook of Applications and Advances of the Rough Sets Theory, pp. 3-18, 1992. [ Links ]
[8] Grzymala-Busse, J.W., The rule induction systems LERS Q: a version for personal computers. in In Proceedings of the International Workshop on Rough Sets and Knowledge Discover, 1993. [ Links ]
[9] Grzymala-Busse, J.W., A new version of the rule induction system LERS. Fundamenta Informaticae, 31, pp. 27-39, 1997. [ Links ]
[10] Grzymala-Busse, J.W. and STEFANOWSKI, J., Three discretization methods for rule induction. International Journal of Intelligent Systems, 16, pp. 29-38, 2001. [ Links ]
[11] Stefanowski, J., The rough set based rule induction technique for classification problems. in In Proceedings of 6th European Conference on Intelligent Techniques and Soft Computing EUFIT 98. Aachen, 1998. [ Links ]
[12] Stefanowski, J., On combined classiffers, rule induction and rough sets. Transactions on Rough Sets VI, Springer LNCS, 4374, pp. 329-350, 2007. [ Links ]
[13] Grzymala-Busse, J.W., MLEM2: A new algorithm for rule induction from imperfect data. in Proceedings of the 9th International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, IPMU 2002. Annecy, France, 2002. [ Links ]
[14] Stefanowski, J. and Nowaczyk, S., On using rule induction in multiple classiffiers with a combiner aggregation strategy. in In Proc. of the 5th Int. Conference on Intelligent Systems Design and Applications - ISDA 2005, IEEE Press, 2005. [ Links ]
[15] Skowron, A., Boolean reasoning for decision rules generation. In: Komorowski. Methodologies for Intelligent Systems. Lectures Notes in Artificial Intelligence Springer, 689, pp. 295-305, 1993. [ Links ]
[16] Stefanowski, J. and Vanderpooten, D., A general two-stage approach to inducing rules from examples. Rough sets, Fuzzy sets and Knowledge Discovery Springer, pp. 317-325, 1994 [ Links ]
[17] Grzymala-Busse, J.W. and Zou, X., Classification strategies using certain and possible rules. Rough sets and current trends in Computing, Lectures Notes in Artificial Intelligence Springer, 1424, pp. 37-44, 1998. [ Links ]
[18] Kryszkiewicz, M., Rough sets approach to rules generation from incomplete information systems. The Encyclopedia of Computer Sciences and Technology, 44, pp. 319-346, 2001. [ Links ]
[19] Leung, Y., et al., Knowledge acquisition in incomplete information systems: A rough set approach. European Journal of Operational Research, 168, pp. 164-180, 2006. [ Links ]
[20] Stefanowski, J., On combined classiffers, rule induction and rough sets. Transactions on Rough Sets VI Springer LNCS, 4374, pp. 329-350, 2007. [ Links ]
[21] Slowinski, R. and Vanderpooten, D,. Similarity relation as a basis for rough approximations, in Advances in Machine Intelligence & Soft-Computing, P.P. Wang, Editor: Durham. pp. 17-33, 1997. [ Links ]
[22] Pawlak, Z., Rough Sets. International journal of Computer and Information Sciences, 11, pp. 341-356, 1982. [ Links ]
[23] Greco, S., Rough sets theory for multicriteria decision analysis. European Journal of Operational Research 129, pp. 1-47, 2001: [ Links ]
[24] Pawlak, Z. and Skowron, A. Rough Sets: Some extensions. Information Sciences, 177, pp. 28-40, 2007. [ Links ]
[25] Qin, K., et al., On Covering Rough Sets. Lectures Notes on Artificial Intelligence, 4481, pp. 34-41, 2007. [ Links ]
[26] Skowron, A., Swiniarski, R. and Synak, P., Approximation Spaces and Information Granulation, in Transactions on Rough Sets III. Lecture Notes in Computer Science, J.F. Peters and A. Skowron, Editors, Springer-Verlag GmbH, 2005, [ Links ]
[27] Slowinski, R. and Vanderpooten, D., A generalized definition of rough approximations based on similarity. EEE Transactions on Data and Knowledge Engineering, 12(2), pp. 331-336, 2000.
[28] Skowron, A. and Stepaniuk, J., Tolerance approximation spaces. Fundamenta Informaticae, 27, pp. 245-253, 1996. [ Links ]
[29] Filiberto, Y., et al., Using PSO and RST to Predict the Resistant Capacity of Connections in Composite Structures. In International Workshop on Nature Inspired Cooperative Strategies for Optimization (NICSO 2010) Springer, pp. 359-370, 2010a. [ Links ]
[30] Filiberto, Y., et al. A method to built similarity relations into extended Rough set theory. in Proceedings of the 10th International Conference on Intelligent Systems Design and Applications (ISDA2010). Cairo, Egipto, 2010b. [ Links ]
[31] Kennedy, J. and Eberhart, R.C. Particle swarm optimization. in In Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, New Jersey: IEEE Service Center, 1995. [ Links ]
[32] Mitra, S., et al., Shadowed c-means: Integrating fuzzy and rough clustering. Pattern Recognition, 43, pp. 1282-1291, 2010. [ Links ]
[33] Science, D.o.I.a.C., UCI Machine Learning Repository, C.U.o.C. Irvine, . Editor: http://www.ics.33.edu/~mlearn/MLRepository.html. [ Links ]
[34] Alcalá, J., et al., KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. Journal of Multiple-Valued Logic and Soft Computing, 2010. [ Links ]
[35] http://www.cs.waikato.ac.nz/Yml/weka/., T.o.o.c.w.i.J.A.u.G.p.l.i., Weka.
[36] http://www-idss.cs.put.poznan.pl/rose, R.R.S.D.E.A.i. [ Links ]













