Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas v.78 n.169 Medellín out. 2011
ESTIMACIÓN DE PARÁMETROS INVARIANTES PARA UN MOTOR DE INDUCCIÓN
INVARIANTS PARAMETER ESTIMATION FOR AN INDUCTION MOTOR
ADOLFO ANDRÉS JARAMILLO-MATTA,
Ph. D., Universidad del Valle, Palmira-Colombia, adolfoajaramillo@gmail.com
EDINSON FRANCO-MEJÍA,
Ph. D. Universidad del Valle, Cali-Colombia, edinson.franco@univalle.edu.co
LUIS GUASCH-PESQUER,
Ph. D., Universidad Rovira i Virgili, Tarragona-España, luis.guasch@urv.cat
Recibido para revisar Abril 25 de 2011, aceptado Agosto 31 de 2011, versión final Septiembre 8 de 2011
RESUMEN: Este artículo muestra un algoritmo que implementa una nueva técnica de estimación de parámetros invariantes para el motor de inducción trifásico con rotor de jaula de ardilla, para dos de los modelos de comportamiento más utilizados: modelo de jaula sencilla y modelo de doble jaula sin pérdidas en el entrehierro. Esta técnica parte únicamente de los datos proporcionados por el fabricante y disminuye de manera considerable los errores identificados con otras técnicas. Los resultados obtenidos se comparan con los datos experimentales de un motor de inducción trifásico de 100 hp de potencia, y muestran diferencias muy marcadas entre el comportamiento obtenido con el modelo de jaula sencilla y el obtenido con el modelo de doble jaula. Esta diferencia puede afectar el desempeño de aplicaciones que incluyen motores de inducción tales como: sistemas de control, análisis, simulación y emulación de los accionamientos eléctricos, entre otros.
PALABRAS CLAVE: Motor de inducción, estimación de parámetros, régimen permanente.
ABSTRACT: This paper shows an algorithm that implements a new technique for estimating invariant parameters for the three-phase induction motor with squirrel cage rotor, for two of the most widely used models: single-cage model and double-cage model without loss on the gap. This technique starts only from the manufacturer data, and significantly improves the errors identified in other techniques. The results are compared with experimental data from a three-phase induction motor of 100 hp, and show marked differences between the behavior obtained with the single-cage model and the obtained one with the double-cage model. This difference may affect the performance of applications which include induction motors, such as control systems, analysis, simulation and emulation of electric drives, among others.
KEYWORDS: Induction motors, parameters estimation, steady state.
1. INTRODUCCIÓN
Los motores de inducción trifásicos son los más utilizados en los accionamientos eléctricos industriales. Las aplicaciones que implementan dichos accionamientos, por lo general implican sistemas y mecanismos de control tanto de par como de velocidad, análisis en régimen permanente y transitorio, sistemas on-line y off-line, entre otros. En todos los casos, el modelo con el cual se analicen, o implementen, dichos motores marca un papel fundamental para que los resultados sean confiables.
Otro tipo de aplicaciones que dependen del modelo del motor de inducción son de orden académico; los análisis realizados a través de simulaciones y/o cálculos matemáticos provienen de un modelo determinado, del cual se espera una representación del comportamiento ajustada al comportamiento real del motor.
El comportamiento del motor de inducción, tanto en régimen estático como dinámico, se puede representar por medio de diferentes modelos [1-3], los cuales son deducidos de acuerdo al comportamiento de la máquina y no a su estructura de construcción. Por tanto, el problema principal en la representación del comportamiento del motor de inducción consiste en que el modelo del motor no es proporcionado por el fabricante y, por ende, tampoco el valor de los parámetros de dicho modelo. En el caso de los modelos utilizados comúnmente, no existe una técnica única ni exacta para determinar el valor de sus parámetros. En cada caso, las técnicas utilizadas realizan supuestos, en función de la aplicación, que contribuyen al cálculo de los parámetros. Dichos parámetros pueden ser variables, invariantes o una combinación de estos.
Por tanto, los dos problemas principales que se abordarán para realizar el estudio del motor de inducción son: la selección de un modelo de comportamiento apropiado y el diseño de una técnica de estimación de los parámetros de dicho modelo, que proporcione un comportamiento simulado confiable en todos los puntos de funcionamiento del motor.
Los errores más comunes identificados en algunas técnicas, previamente existentes, para determinar el valor de los parámetros se presentan en tres zonas de funcionamiento: la zona de funcionamiento inestable, el punto de par máximo y el punto de par de arranque del motor de inducción.
Algunas técnicas que presentan buenos resultados, [4-7], no se pueden reproducir a cabalidad bien sea por que la aplicación para la cual fue diseñada es específica o por falta de detalle en el procedimiento de reproducción de dicha técnica.
Otro problema presentado en la estimación de los parámetros se refiere a la cantidad de datos que se utilizan como referencia para dicho proceso. Por un lado se tienen los datos proporcionados por el fabricante, que presentan la ventaja de no requerir medidas experimentales, y por otro lado se tienen los datos experimentales, que deben ser realizados en laboratorios equipados para tal fin. Este último caso solamente puede aplicarse para un determinado número de motores, ya que la instrumentación necesaria no siempre está disponible, o el proceso en el cual se encuentra acoplado el motor no lo permite.
En este artículo se diseña un algoritmo de estimación de parámetros invariantes para los modelos de jaula sencilla y doble jaula sin pérdidas en el entrehierro, para el motor de inducción trifásico. Para estimar los parámetros dicho algoritmo parte únicamente de los datos proporcionados por el fabricante, DF, evitando la necesidad de datos experimentales, DE. La técnica fue probada con los datos experimentales de un motor de inducción trifásico Westinghouse de 100 hp, 1764 r/min, 4 polos, y rotor con estructura jaula de ardilla sencilla, mostrado en este artículo, y posteriormente con dos motores de 370 W (Elwe) y 560 kW (Siemens), para comprobar su efectividad.
2. MODELOS UTILIZADOS
Aunque existen diferentes modelos para el motor de inducción trifásico [1-3], en este artículo se analizan los modelos de jaula sencilla y doble jaula para la representación del comportamiento del motor de inducción y para la estimación de sus parámetros.
Las ecuaciones diferenciales no lineales de estos modelos se muestran en el sistema de ecuaciones (1).
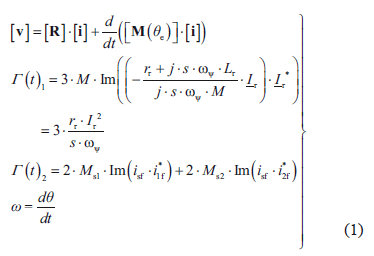
El par calculado se diferencia para el modelo de jaula sencilla y doble jaula, con los subíndices 1 y 2, respectivamente. Dichas ecuaciones rigen el funcionamiento transitorio de las máquinas de inducción. La Figura 1 muestra la representación en circuitos eléctricos de estos modelos; en ella se diferencian el estator, el rotor y el circuito magnético del entrehierro con los subíndices s, r y m, respectivamente.
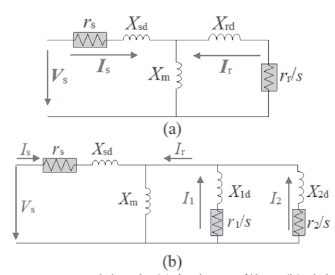
Figura 1. Modelos de (a) jaula sencilla y (b) doble jaula de la máquina de inducción
Para todos los casos, las resistencias representan las perdidas eléctricas y las inductancias representan los flujos: útil del campo magnético y de dispersión en la maquina.
Las siguientes hipótesis han sido utilizadas para simplificar las ecuaciones de los modelos:
- Eje mecánico como única interfaz de salida hacia la carga, por medio de dos variables: Par y velocidad.
- Estator y rotor lisos (entrehierro constante). Se desprecian los efectos producidos por el ranurado del estator y del rotor en el valor de las inductancias propias y mutuas de los bobinados.
- Máquina con topología simétrica (bobinas del estator iguales entre si y bobinas del rotor iguales entre sí)
- Permeabilidad magnética del hierro elevada (reluctancia magnética despreciable frente a la del entrehierro)
- Comportamiento magnético del hierro lineal, es decir, no se consideran los efectos de saturación e histéresis. El numero de fases y el número de pares de polos del rotor siempre coincide con los del estator. Esta coincidencia no es necesaria, pero simplifica los modelos.
- Distribución sinusoidal del campo en el entrehierro. Las fuerzas magneto motrices debidas a los bobinados del estator siguen una distribución sinusoidal espacial a lo largo del entrehierro, despreciándose las armónicas espaciales.
3. ESTIMACIÓN DE LOS PARÁMETROS
Para realizar el análisis se tomarán dos tipos de datos de partida de la máquina analizada: experimentales y proporcionados por el fabricante.
3.1 Datos experimentales. Se han obtenido 17 datos experimentales que pueden representarse por medio de puntos en la curva par-velocidad de la Figura 3, que muestra la característica mecánica de la máquina en valores pu (por unidad). Estos datos se registran en la Tabla 1.
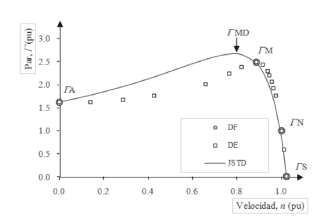
Figura 3. Curva característica obtenida con los parámetros del modelo de jaula sencilla
Tabla 1. Puntos experimentales de la máquina de 100 hp.
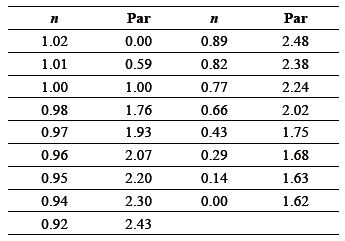
3.2 Datos proporcionados por el fabricante: los datos proporcionados por el fabricante se representan por los puntos: par de arranque (ΓA), par máximo (ΓM), par nominal (ΓN) y par de sincronismo (ΓS) en la Figura 3 y sus valores se encuentran en la Tabla 2.
Tabla 2. Puntos proporcionados por el fabricante.
3.3 Técnica Implementada. La Figura 2 muestra el diagrama de flujo del algoritmo implementado para los modelos de jaula sencilla y doble jaula. En la bibliografía de referencia, la variable utilizada para determinar el error es poco mencionada; esta variable puede ser la impedancia de entrada del circuito equivalente (Zin), la corriente (I) o el par (Γ) en los datos de entrada al algoritmo, etc. En el bloque “Referencia de Error" se ha seleccionado el valor de par (Γ) en todo el rango de funcionamiento. Dicho error se ha determinado para no sobrepasar el valor de error máximo permitido de 0.1%.
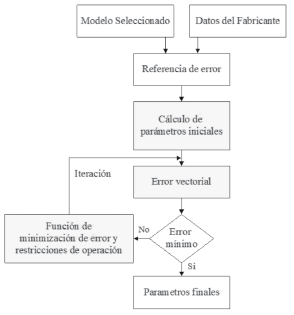
Figura 2. Algoritmo de estimación de parámetros con minimización de error.
El bloque “Cálculo de parámetros iniciales" es de gran relevancia, ya que debido a las restricciones de operación de esta técnica, los valores finales de los parámetros convergen de manera satisfactoria cuando los parámetros iniciales son los adecuados. En este bloque se genera un primer conjunto de parámetros como base para calcular el error del comportamiento obtenido. Para el caso analizado, los valores iniciales se calculan como en [7], debido a que presenta un error aceptable en los puntos de funcionamiento proporcionados por el fabricante. Con los valores de par obtenidos con los parámetros iniciales se calcula el error a minimizar en el bloque “Error vectorial", ev. Este error se calcula por medio de la distancia entre el punto de par dado por el fabricante y el punto de par obtenido por la simulación. La expresión (2) es utilizada para calcular el error ev.
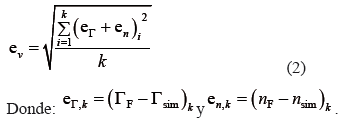
En estas expresiones el subíndice F es el valor dado por el fabricante, el subíndice sim corresponde a los valores simulados y k es el punto de funcionamiento evaluado.
Una vez se calcula el error vectorial, el bloque de decisión “Error mínimo" verifica que las condiciones de error mínimo se cumplan. En caso de no cumplirse, el algoritmo ingresa al bloque de “Función de minimización de error y restricciones de operación", donde se generan nuevos valores de los parámetros que disminuyen el error obtenido con la simulación. Dicha minimización es realizada por métodos de mínimos cuadrados (Levenberg-Marquardt) como en [5, 8-13]; esto genera un ciclo de iteraciones que deben cumplir con las siguientes restricciones de operación:
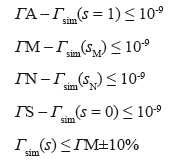
En cada iteración la función de minimización de error cambia el valor de los parámetros variando en ±2% el valor anterior de cada parámetro. Los parámetros varían en el siguiente orden: rr, rs, Xsd, Xrd, Xm.
Para el cálculo del error, es importante notar que los algoritmos que parten de los datos del fabricante como en [4, 7, 13, 14], calculan el error total únicamente en los puntos de funcionamiento de arranque, par máximo, condiciones nominales y sincronismo. Adicionalmente, el algoritmo es configurado para que todos los valores de los parámetros sean mayores que cero y para que cada iteración se produzca hasta alcanzar el valor predeterminado de error mínimo o hasta que se cumpla un tiempo máximo de iteración. Este procedimiento permite obtener el valor de los parámetros que determinan un error mínimo en todo el conjunto de puntos de operación.
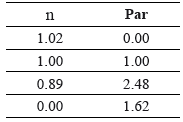
3.4 Parámetros estimados. En la Tabla 3 se registran los parámetros estimados con la técnica diseñada para los modelos de jaula sencilla y doble jaula. La Figura 3 muestra el comportamiento obtenido con los parámetros estimados para el modelo de jaula sencilla. Además, muestra los puntos proporcionados por el fabricante: ΓA, ΓM, ΓN y ΓS (DF, en círculos) y los datos experimentales de la máquina (DE, en cuadrados).
Tabla 3. Parámetros en pu, estimados con la técnica diseñada

También puede visualizarse el par máximo obtenido con la técnica diseñada, ΓMD, donde se nota claramente que las coordenadas de dicho par son diferentes a las del punto de par máximo proporcionado por el fabricante. En esta figura, el comportamiento simulado se ajusta muy bien a las coordenadas de los puntos ΓS, ΓM, ΓN y ΓS. Sin embargo, no presenta un buen ajuste en los demás puntos de funcionamiento experimental de la máquina.
La Figura 4 muestra el comportamiento obtenido con los parámetros del modelo de doble jaula, estimados con la técnica diseñada (Tabla 3). En este caso, los valores de par simulado se ajustan muy bien a los cuatro puntos de funcionamiento proporcionados por el fabricante, además de mostrar una disminución significativa en el ajuste con los puntos de funcionamiento experimental, DE.
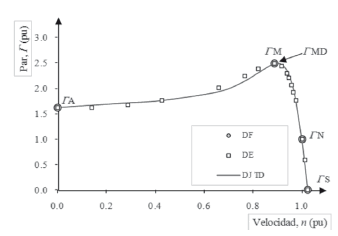
Figura 4. Curva característica obtenida con los parámetros del modelo de doble jaula
El error calculado en cada punto de funcionamiento proporcionado por el fabricante, tanto con los parámetros de jaula sencilla como con los de doble jaula, se muestran en la Tabla 4. Cuando el error contiene el signo *, significa que el valor del par simulado en ese punto es mayor que el valor de par experimental (es decir, error negativo); en esta tabla también se muestra el error total, eT, calculado por medio de la expresión para el error cuadrático medio (3) en todos los puntos proporcionados por el fabricante.
Tabla 4. Error (%) calculado en los datos proporcionados por el fabricante.

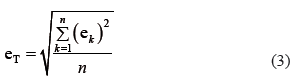
Los errores mostrados en la Tabla 4 reflejan el gran ajuste que presentan ambos modelos en los puntos proporcionados por el fabricante.
Los análisis realizados en este artículo han sido sobre motores de inducción comerciales, con estructura en el rotor de jaula sencilla. Sin embargo, el modelo de doble jaula presenta un mejor ajuste en todos los puntos de funcionamiento. Esto podría atribuirse a la limitación de grados de libertad que presenta el modelo de jaula sencilla frente al modelo de doble jaula (cantidad de parámetros), lo cual ha sido discutido en trabajos como [4,7-8]. Los resultados de este trabajo muestran que el modelo de jaula sencilla puede ser utilizado de manera confiable en aplicaciones de régimen estático y en la zona de funcionamiento estable, cercana al punto de funcionamiento nominal. Sin embargo, el modelo de doble jaula sin pérdidas en el entrehierro, aunque presenta mejor comportamiento en todos los puntos de funcionamiento, aún presenta errores en la zona de funcionamiento inestable. Por otro lado, el ajuste de los modelos al comportamiento experimental del motor depende directamente de la precisión de las distintas técnicas utilizadas actualmente para la estimación del valor de los parámetros [4-5,13-14]. Por lo cual se hace necesario realizar estudios más profundos en este tema en investigaciones posteriores.
4. CONCLUSIONES
En este artículo se diseña una técnica de estimación de parámetros que parte únicamente de los datos proporcionados por el fabricante y que determina un buen comportamiento del motor tanto en la zona de funcionamiento estable como en la inestable. Los resultados muestran grandes diferencias entre los comportamientos obtenidos cuando se utilizan los modelos de jaula sencilla y doble jaula, principalmente en la zona de funcionamiento inestable y en el punto de par máximo. Estas diferencias pueden cambiar la representación del comportamiento del motor, desencadenando errores como fallas en el ajuste del sistema de control y selección de elementos actuadores de potencia, entre otros.
NOMENCLATURA

REFERENCIAS
[1] Guasch-Pesquer, L., and Ciumbulea,G. E., Maquinas y Accionamientos Eléctricos. Barcelona: Marcombo, 2004. [ Links ]
[2] Corteletti, R., Barros, P. R. and Lima, A. M. N., Parameters estimation of induction motor using subspace methods, in IEEE International Symposium on Industrial Electronics. ISIE 03, Vol. 2, pp. 667-671, 2003. [ Links ]
[3] Franco, E., Amaya, M. and Ramirez, J., A new model for induction motor with induced saliencies, in Int. Conf. on Industrial Electronics and Control Applications. ICIECA 2005. 6 P. [ Links ]
[4] Pedra, J., Candela, I. and Sainz, L., Modelling of squirrel-cage induction motors for electromagnetic transient programs, IET Electric Power Applications, Vol. 3, pp. 111-122, 2009. [ Links ]
[5] Mirafzal, B., Skibinski,G. L. and Tallam,R. M., Determination of Parameters in the Universal Induction Motor Model, IEEE Transactions on Industry Applications, Vol. 45, pp. 142-151, 2009. [ Links ]
[6] Rao, M. R., Estimation of parameters for induction motors analytical model by direct search method, in Int. Conf. on Electrical Machines and Systems, ICEMS, pp. 8-10, 2008. [ Links ]
[7] Pedra, J., On the Determination of Induction Motor Parameters From Manufacturer Data for Electromagnetic Transient Programs, IEEE Transactions on Power Systems, Vol. 23, pp. 1709-1718, 2008. [ Links ]
[8] Corcoles, F., Pedra, J., Salichs, M. and Sainz, L., Analysis of the induction machine parameter identification, IEEE transactions on Energy conversion, Vol. 17, pp. 183-190, 2002. [ Links ]
[9] M. Cirrincione, M. Pucci, G. Cirrincione, and G. A. Capolino, A new experimental application of least-squares techniques for the estimation of the induction motor parameters," IEEE Transactions on Industry Applications, vol. 39, pp. 1247-1256, 2003. [ Links ]
[10] Cirrincione, M., Pucci, M., Cirrincione, G. and Capolino, G. A., Constrained least-squares method for the estimation of the electrical parameters of an induction motor, COMPEL, Vol. 22-4, pp. 1089-1101, 2003. [ Links ]
[11] Pedra, J. and Corcoles, F. Estimation of induction motor double-cage model parameters from manufacturer data, IEEE transactions on Energy conversion, Vol. 19, pp. 310-317, 2004. [ Links ]
[12] Benaidja, N. and Khenfer, N. Identification of Asynchronous Machine Parameters by Evolutionary Techniques, Electric Power Components and Systems, Vol. 34, pp. 1359–1376, 2006. [ Links ]
[13] Pedra, J. and Sainz, L., Parameter estimation of squirrel-cage induction motors without torque measurements, IEE Proceedings Electric Power Applications, Vol. 153, pp. 263-270, 2006. [ Links ]
[14] Haque, M. H., Determination of NEMA Design Induction Motor Parameters From Manufacturer Data, IEEE transactions on Energy conversion, Vol. 23, pp. 997-1004, 2008. [ Links ]













