Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.78 no.169 Medellín Oct. 2011
MODELADO DE DINÁMICA DE FLUIDOS Y TRANSFERENCIA DE CALOR Y MASA EN PROCESOS AGROALIMENTARIOS POR MÉTODO DE VOLÚMENES FINITOS
FLUID DYNAMICS, HEAT AND MASS TRANSFER MODELING BY FINITE VOLUME METHOD FOR AGROFOOD PROCESSES
NELSON O. MORAGA
PhD., Universidad de La Serena. nmoraga@userena.cl
CARLOS E. ZAMBRA
Dr., Universidad Arturo Prat, carlos.zambra.s@gmail.com
PAUL B. TORRES
MSc., Universidad de Santiago de Chile. paultorresj@gmail.cl
ROBERTO A. LEMUS-MONDACA
MSc., Universidad de Santiago de Chile y Universidad de La Serena, roberto.lemusm@usach.cl, rlemus@userena.cl
Recibido para revisar Enero 20 de 2011 , aceptado Junio 30 de 2011, versión final Julio 8 de 2011
RESUMEN: Se describe la transferencia de momento, calor y masa transitorio bi-dimensional en procesos agroalimentarios. Estos procesos son: la pre-cosecha y la deshidratación por aire caliente de frutas. La metodología incluye modelación matemática y simulación computacional para describir la convección y difusión de calor y masa conjugada que resulta de la interacción entre el alimento y el aire. El modelo matemático emplea las ecuaciones diferenciales parciales no lineales acopladas de continuidad, momento lineal, energía y materia. Se considera que las propiedades físicas de las frutas calculadas mediante correlaciones empíricas, varían con la temperatura y la concentración de humedad. El método de volúmenes finitos junto el algoritmo SIMPLE se utiliza para obtener los resultados de la variación en el tiempo de las distribuciones de velocidades (v), temperaturas (T) y concentraciones de humedad (C) para los procesos en estudio. Las propiedades termofísicas variables de los alimentos se obtuvieron a partir de modelos empíricos. Los resultados obtenidos incluyen distribuciones de las variables dependientes (v, T, C) en el tiempo, los cuales se comparan con resultados experimentales y numéricos de la literatura especializada.
PALABRAS CLAVE: Convección mixta/forzada; simulación numérica; proceso térmicos.
ABSTRACT: The two-dimensional transient momentum, heat and mass transfer for agrofood processes is described. These processes are: pre-harvest and fruit hot-air dehydration. The methodology includes mathematical modeling and computational simulation to describe conjugate heat and mass convection and diffusion between food and surrounding air. The mathematical model is written in terms of a system built based on the non-linear coupled partial differential equations of continuity, linear momentum, energy and mass. Temperature and concentration dependent fruit thermophysical properties were calculated from empirical models. The finite volume method with the SIMPLE algorithm is used to obtain the results of velocity (v), temperature (T) and moisture concentration (C) distributions in time for the processes studied. The validation procedure includes a comparison with v, T and C experimental and numerical results obtained in the specialized literature.
KEYWORDS: Preharvest; drying; forced/mixed convection; numerical simulation.
1. INTRODUCCIÓN
Chile puede ser una Potencia Alimentaria mundial. Los antecedentes indican que es el segundo sector en generación de divisas, después del cobre [1]. Desde hace algunos años la calidad es el denominador común de todos los productos agrarios en sus diferentes presentaciones: frescos y procesados. Las empresas dedicadas a la exportación y producción de alimentos hacia los mercados internacionales, pierden grandes cantidades de productos por daños superficiales debido a los factores climáticos. Es así que en la pre-cosecha, los frutos deben estar en buenas condiciones para asegurar la calidad del producto procesado o de consumo directo.
Entre las frutas chilenas con mayor exportación y demanda hacia los mercados internacionales se encuentran: uvas, kiwis y duraznos y con mayor expectativas de exportación se presentan las cerezas [1]. Es por ello, que este estudio se enfoca en estas frutas que presentan una gran susceptibilidad a los cambios bruscos de temperaturas, humedad relativa y vientos fuertes provocados por el medio ambiente. Los daños más comunes que presentan estas frutas son por enfriamiento, pérdida de humedad, sobre maduración, caída al suelo y manipulación [2]. Hoy día se sabe que la calidad de las frutas y hortalizas viene determinada por diversos factores que intervienen durante su desarrollo en la planta, incluyendo los eventos que tienen lugar antes de la cosecha.
El secado es uno de los procesos térmicos más utilizados para la conservación de alimentos, otorgando prolongada vida útil y gran diversidad de productos secos, además de la reducción sustancial del peso y volumen de éstos lo que influye en una reducción importante de los costos de empaque, almacenamiento y transporte [3]. Varios cambios físicos, químicos y nutricionales ocurren durante el secado de alimentos, los cuales se ven afectados por diferentes parámetros del propio tratamiento de secado. Los parámetros externos incluyen: temperatura, velocidad y humedad relativa del aire de secado, mientras que los propiedades termofísicas incluyen: conductividad térmica, difusividad térmica, calor específico, densidad y difusividad de materia [4].
El comportamiento de los fluidos que cubren cuerpos de diferentes geometrías complejas se ha estudiado en variadas aplicaciones de la rama de la ingeniería y la física de fluidos. La utilización de los fluidos en la conservación de alimentos presenta una gran variedad de aplicaciones [3, 4, 5, 6]. Sin embargo, la mayoría de estas aplicaciones se han basado principalmente en las condiciones de almacenamiento y procesamiento térmico de los alimentos. Escasa importancia se ha dado a una etapa de importancia que es la maduración y conservación del fruto en la pre-cosecha [7]. Por lo tanto, se entiende que la transferencia de calor y masa se deben predecir para mejorar las condiciones de los procesos [4]. Los mecanismos de transporte involucrados en estos procesos han incluido convección mixta, forzada o natural, en ductos o cavidades rectangulares con diferentes fluidos (aire y agua) [8]. La geometría utilizada para los alimentos ha sido: rectangular, esférica y cilíndrica [6,9].
El principal objetivo de este trabajo es caracterizar numéricamente la dinámica de fluidos y la transferencia de calor y masa conjugada durante la pre-cosecha y secado de frutas que presentan una gran susceptibilidad a cambios bruscos de temperaturas, humedad relativa y vientos fuertes provocados por el medio ambiente.
2. CASOS DE ESTUDIO
2.1 Caso 1: Pre-Cosecha
El proceso de convección-difusión transitorio 2D de fluido exterior (aire) alrededor de frutos esféricos se ilustra en la Figura 1. La altura del dominio de cálculo es 10 veces mayor que la longitud característica L, que se indica para cada caso en estudio. La dirección del flujo es de izquierda a derecha.
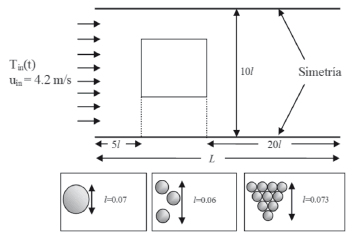
Figura 1. Situación física de convección-difusión alrededor de frutos esféricos.
Las propiedades del aire: viscosidad cinemática (n, m2/s), difusividad térmica (α, m2/s) y coeficiente de expansión térmica (β, 1/T) se consideran que varían en el rango de temperaturas Tmín=280 K y Tmáx=294 K [10].
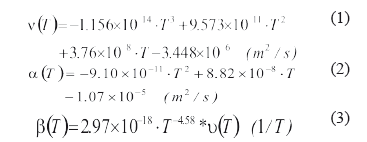
La ecuación 4 muestra las condiciones iniciales del aire que ingresa con una temperatura (K) que varía en el tiempo (s) a lo largo de un día y una noche, entre 276 a 294 K. La velocidad de entrada se considera uniforme uin=4.2 m/s. Las condiciones de borde de las paredes presentan simetría y no deslizamiento en la parte superior e inferior del dominio. A la salida se considera flujo desarrollado.
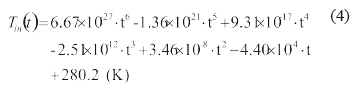
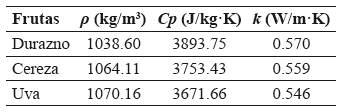
En la Tabla 1 se presentan las propiedades termofísicas obtenidas por medio de ecuaciones empíricas calculadas con la metodología descrita por [11], las cuales necesitan del análisis proximal realizado para cada uno de los frutos. Las propiedades térmicas (densidad: ρ; conductividad térmica: k y calor específico: Cp) de las frutas permanecen constantes a lo largo del tiempo de cálculo.
Tabla 1. Propiedades térmicas de las frutas en estudio.
2.2 Caso 2: Secado
La Figura 2 muestra el dominio del problema, con las correspondientes condiciones iniciales y de borde, para la evaluación de los campos de flujo, temperatura y concentración de humedad del fluido (aire de secado) alrededor del fruto (kiwi). En este caso se presenta una convección mixta en una sección transversal para el flujo del fluido.
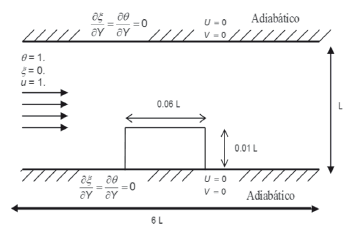
Figura 2. Situación física de convección-difusión alrededor del fruto rectangular.
Las propiedades termofísicas utilizadas para el kiwi dependen de la temperatura y la concentración de humedad, tal como lo reportaron [4].
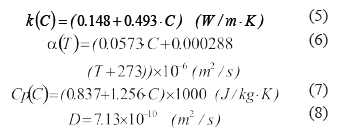
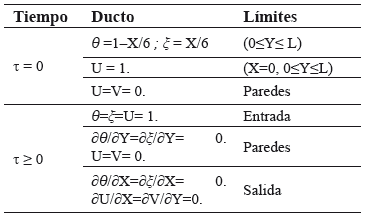
Las condiciones de borde de las variables de transferencia de momento (U y V), calor (θ) y masa (ξ) adimensionales, son:
Tabla 2. Condiciones iniciales y de borde.
3. MODELO MATEMÁTICO
Las ecuaciones diferenciales parciales que describen el movimiento por convección y difusión transitorio 2D son las ecuaciones de Navier-Stokes. Las ecuaciones que describen el transporte de calor y masa se basan en la segunda ley de Fourier y Fick, respectivamente. Las suposiciones consideran: fluido Newtoniano e incompresible, flujo laminar y sin disipación energía viscosa; y en el alimento, sin generación interna de calor, donde el encogimiento y deformación son despreciables. La forma de estas ecuaciones dimensionales se resume así:
Ecuación de continuidad:
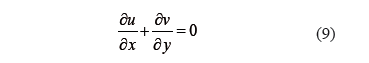
Ecuación de momento lineal x:
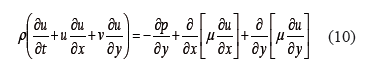
Ecuación de momento lineal y:
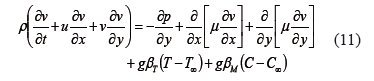
Ecuación de transferencia de calor:
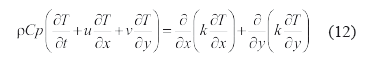
Ecuación de transferencia de masa:
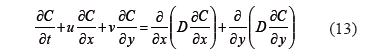
Ahora, considerando la adimensionalización de las variables utilizadas (U, V, θ y ξ) para el fluido y el alimento, se tiene que [8]:
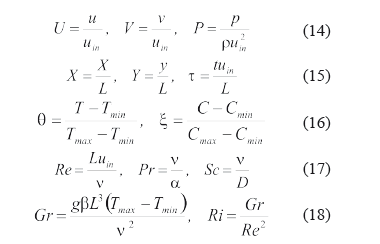
De este modo el modelo adimensional queda expresado como:
Ecuación de continuidad:
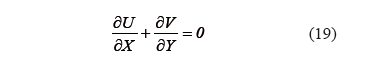
Ecuación de momento lineal x:
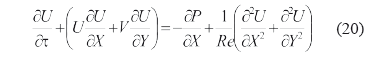
Ecuación de momento lineal y:
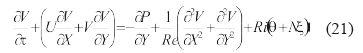
Ecuación de transferencia calor:
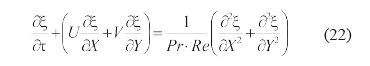
Ecuación de transferencia masa:
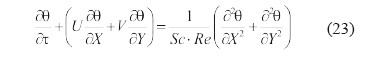
Ecuaciones de transferencia calor y masa para el alimento:
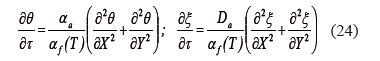
4. PROCEDIMIENTO COMPUTACIONAL
El sistema de ecuaciones diferenciales, parciales, no lineales acopladas con las condiciones iniciales y de borde se resolvió con el método de volúmenes finitos (FVM) usando el algoritmo SIMPLE [12]. En los casos de pre-cosecha y secado dos mallas no uniformes alternativas se emplearon para cada cálculo computacional, con 110x80 nodos (durazno), 118x106 (cerezas), 154x132 (uvas) y 102x82 en el secado. Una densidad más alta de nodos se localizó cerca del subdominio donde se encuentra el fruto (Figura 3). El paso de tiempo dimensional (t) constante utilizado en la pre-cosecha de frutas esféricas, es de 0.01 segundos. En cambio, el paso de tiempo adimensional (τ) constante utilizado en el ejemplo de secado, es de 0.001.
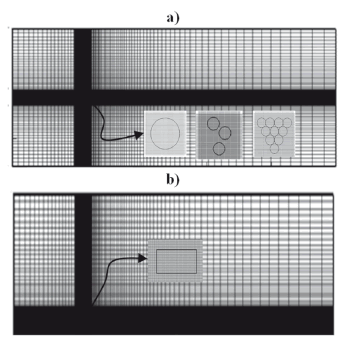
Figura 3. Mallas del dominio computacional para los dos casos: a) pre-cosecha y b) secado.
Una ley de quinta potencia se utilizó para calcular los términos convectivos [12], mientras que los términos difusivos se determinaron usando funciones de interpolación lineal para las variables dependientes (v, T y C) entre los nodos.
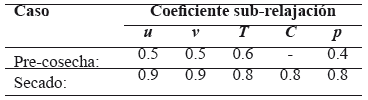
La Tabla 3 muestra los coeficientes de sub-relajación usados en el proceso iterativo de cálculo, para las dos componentes de la velocidad (u-v), temperatura (T), concentración de humedad (C) y presión (P) [8].
Tabla 3. Coeficientes de sub-relajación utilizados para la velocidad, temperatura, concentración y presión.
El criterio de convergencia aplicado para detener los cálculos de velocidad, temperatura y concentración en cada paso de tiempo para cada nodo y en cada instante de tiempo fue:
![]()
5. RESULTADOS Y DISCUSIÓN
Caso 1: La Figura 4 muestra las líneas de corriente que se forman cuando el aire pasa por sobre los frutos en dos tiempos diferentes, 0.05 y 25 segundos, para cada fruta en estudio. La simulación en el caso de un durazno para 0.05 segundos presenta dos vórtices simétricos de longitud 0.09 m. En el mismo tiempo anterior, en el caso de tres y diez frutos se forman vórtices de diferentes longitudes debido a la forma de distribución de los frutos. A los 25s los vórtices cambian de tamaño y forma con oscilaciones y variaciones en la componente v de la velocidad. Desde el punto de vista agrícola, la recirculación de aire con cambios de velocidad y temperatura a lo largo del día y noche que se producen detrás de los frutos, pudiese provocar a los frutos movimientos que los hicieran desprenderse del árbol, afectando la calidad del fruto por daño mecánico y posteriores reacciones bioquímicas.
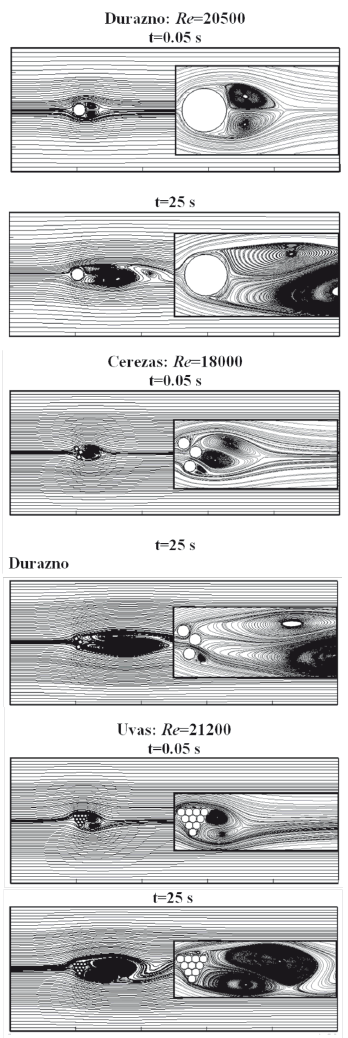
Figura 4. Líneas de corriente para el caso 1: a) durazno, b) cerezas y c) uvas.
Además, en la Figura 4 se muestra un acercamiento con las longitudes de las recirculaciones del aire sobre los frutos, los cuales presentan diferentes longitudes características. La posible generación de vórtices se debe que en la parte de atrás de los frutos el gradiente de presión es mayor que cuando el fluido se enfrenta a ellos, lo cual provoca un flujo de retroceso hacia la zona de capa límite [13]. Los vórtices inicialmente son estacionarios pero a medida que crecen cambian en el tiempo apareciendo a uno y otro lado de los frutos, generando los llamados vórtices de von Karman [13, 14].
Los autores [14] analizaron el efecto del espaciado sobre la emisión de vórtices para un flujo laminar entre cilíndricos de igual diámetro en fila. Ellos identificaron que al aumentar el espaciado las zonas de recirculación disminuyen, existiendo un mayor paso del flujo sobre los cuerpos. En el estudio de Lima e Silva et al. (2003) [13] trabajando con flujo de fluidos sobre cuerpos cilíndricos variando el número de Reynolds en función de la velocidad, mostraron que la longitud de la recirculación detrás del cilindro aumentaba.
En la bibliografía analizada [4, 5, 9] se realizan dos tipos de estudios, primero se comienza con un análisis solo de convección de calor y materia alrededor del cuerpo calculando los coeficientes convectivos locales a lo largo del objeto. Luego con estos valores de coeficientes convectivos se incluyen en las condiciones de borde para el análisis de difusión de calor sobre el objeto [4, 5,15]. Los estudios antes mencionados se basan en análisis de procesos térmicos de conservación de alimentos, congelación y deshidratación. Sin embargo se vio la necesidad de realizar un estudio para la pre-cosecha de frutas, las cuales se ven afectadas por las distintas variaciones de temperaturas que se producen en el día y la noche, pudiendo de esta manera causar graves daños en el fruto.
La Figura 5 muestra las distribuciones de temperaturas para los tres frutas de la pre-cosecha a diferentes pasos de tiempo hasta completar el ciclo día-noche. Como se puede observar los gradientes de temperatura presentan simetría en todos los casos desde la superficie hasta el centro del fruto. Esta condición se puede deber a que los valores de los coeficientes convectivos presentaron pequeñas diferencias, asumiendo un valor promedio alrededor de todo el fruto.
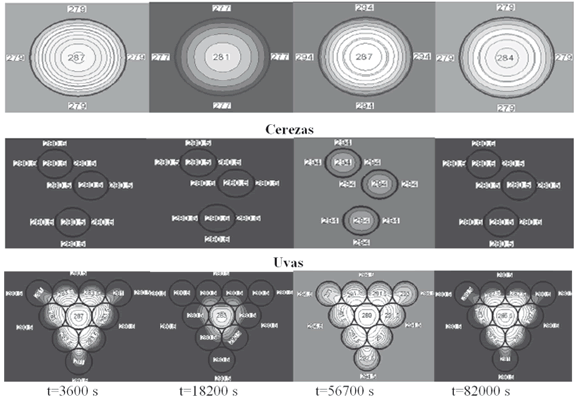
Figura 5. Distribuciones de temperaturas para los tres casos en estudio en diferentes tiempos hasta completar el ciclo día-noche (To: 15.6°C; to: 0 min).
Otra explicación de este caso, es que la transferencia de calor se produce en una zona abierta, observándose que en los primeros instantes de tiempo el flujo de aire viene en dirección frontal al fruto, y que luego lo cubre completamente debido a su alta velocidad. En otros estudios el valor de la velocidad es pequeño por lo que la variación del coeficiente convectivo es muy alta en la superficie y se puede observar que dentro de los alimentos los campos de temperaturas son asimétricos y un desplazamiento en dirección del flujo de aire de la región donde la temperatura es más alta ocurre durante el proceso [4, 7].
Caso 2: Las isotermas (Figura 6) e iso concentraciones (Figura 7) que se muestran dentro del alimento, en una primera etapa del proceso de secado son de forma uniforme, desde la superficie hacia el interior. Sin embargo, luego alcanzando un tiempo t>0.5 se empieza a notar una distribución diagonal desde la izquierda hacia la derecha debido a que el flujo entra por el lado izquierdo con una mayor temperatura y menor concentración, con respecto al alimento. Resultados similares fueron encontrados por [4], utilizando la misma condición inicial y borde, y propiedades del aire como del fruto, sin embargo en el presente trabajo el modelo utilizado no requirió de la obtención de los coeficientes de transferencia de calor y masa.
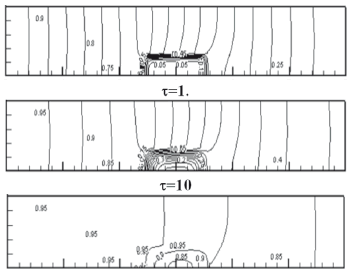
Figura 6. Evolución temporal de las isotermas para el caso 2 (To: 4°C; to: 0 min).
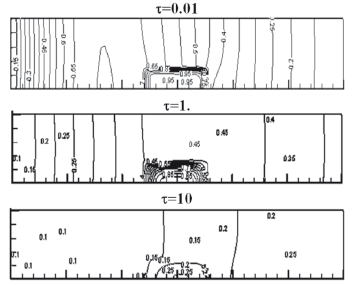
Figura 7. Evolución temporal de las iso-concentraciones para el caso 2 (Co: 4.26 kg agua/kg m.s.; to: 0 min).
En la variación de la temperatura en el centro del alimento, que muestra la Figura 8a, se observa que aumenta con el tiempo de secado ya que la temperatura del aire de secado es mayor que la temperatura del alimento. En este caso la tendencia es muy similar en casi todo el tiempo de secado. En la variación temporal de la concentración de humedad en el centro del alimento, que describe la Figura 8b, se aprecia que la concentración del alimento disminuye con el tiempo de secado debido a que la concentración del aire de secado es menor que la concentración del alimento. La temperatura del aire de secado es de 50°C con una velocidad de entrada de 0.3 m/s, como ha sido descrito por [4].
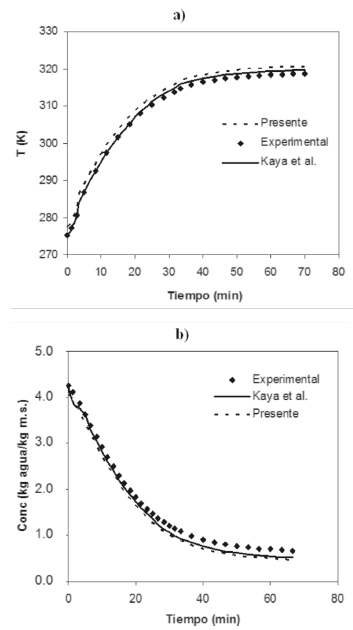
Figura 8. Comparación entre los valores calculados y experimentales para el caso 2: a) temperatura y b) concentración.
En la Figura 9 se muestra el resultado de la distribución de temperatura en el alimento transcurridos 10 minutos y para la concentración de agua a los 30 minutos. Estos tiempos corresponden a los mismos entregados por [4]. Como se puede ver en las figuras las distribuciones tanto de temperaturas y concentraciones con los mayores valores son asimétricas en sentido de izquierda a derecha (entrada del aire). En este caso las distribuciones se expresan adimensionalmente, con valores calculados muy cercanos a los reportados por [4], para este estudio de validación.
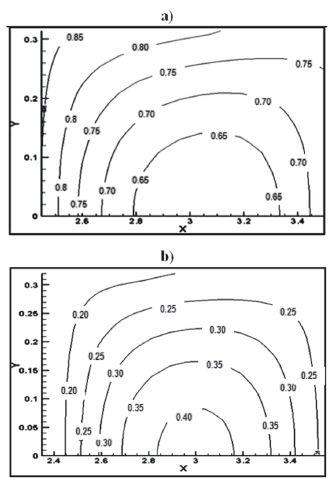
Figura 9. Distribución a) temperaturas y b) concentraciones de humedad en el fruto.
6. CONCLUSIONES
El efecto combinado de la variación de velocidad del aire y la temperatura ambiente en el enfriamiento de frutas (duraznos, cerezas y uvas) se ha descrito para especies individuales y grupos de tres y de diez frutos. Se concluye que la simulación computacional 2D se puede efectuar empleando un modelo conjugado de convección forzada en el aire con uno de difusión de calor con mallas variables. Los resultados de mecánica de fluidos y transferencia de calor obtenidos permiten concluir que empleando simulaciones computacionales se podrían predecir el comportamiento de los frutos a los diferentes cambios climáticos durante el ciclo día-noche (velocidad, humedad y temperatura del aire), disminuyendo costos agrícolas y mejorar la calidad final. En cuanto a la caracterización del proceso de secado, se concluye que los resultados de las distribuciones de temperaturas y humedad del kiwi, calculados con el MVF y programas propios, representa una generalización de los resultados reportados en la literatura, utilizando programas comerciales. Finalmente, se concluye que el empleo de un modelo conjugado para describir simultáneamente la convección de calor y materia en el aire ambiente junto con la difusión de calor y masa en alimentos como se ha propuesto en este trabajo, permite efectuar la predicción del secado, sin un conocimiento previo de los coeficientes convectivo de calor y masa. Precisamente, una ventaja de la metodología propuesta, es que estos coeficientes de transporte puedan obtenerse a posteriori, después de haber calculado las distribuciones de temperatura y humedad tanto en el aire como en el alimento.
AGRADECIMIENTOS
Los autores agradecen a CONICYT-Chile el apoyo recibido en el proyecto FONDECYT 1111067. Roberto Lemus agradece el aporte financiero de la Beca Nacional de Postgrado de CONICYT-Chile.
NOMENCLATURA

REFERENCIAS
[1] Chile Alimentos. Asociación de Empresas de Alimentos de Chile (www.chilealimentos.com). Acceso 10 de Junio de 2011. [ Links ]
[2] Laurie, S. and Crisosto, C., Chilling injury in peach and nectarine, Postharvest Biol Technol; 37, pp. 195-208, 2005. [ Links ]
[3] Akpinar, E. Determination of suitable thin layer drying curve model for some vegetables and fruits, J Food Eng; 73, pp. 75-84, 2006. [ Links ]
[4] Kaya, A., Aydin, O. and Dincer, I., Experimental and numerical investigation of heat and mass transfer during drying of Hayward kiwi fruit, J Food Eng; 88, pp. 323-330, 2008. [ Links ]
[5] Moraga, M. and Medina, E., Conjugate forced convection and heat conduction with freezing of water content in a plate shaped food, Int J Heat Mass Transfer; 43, pp. 53-67, 2000. [ Links ]
[6] Arboleda, D., Valencia, V., Espinosa, J. and Ochoa, O., Mathematical modeling for the thermal process of cylindrical meat products. DYNA, 77(164), pp. 301-307. 2010. [ Links ]
[7] Aswaney, M. Forced - air precooling of fruits and vegetables. Air Conditioning Refrig J; March, pp. 57-62, 2007. [ Links ]
[8] Moraga, N., Riquelme, J., Jauriat, L. Unsteady conjugate water/air mixed convection in a square cavity, Int J Heat Mass Transfer; 52, pp. 5512-5524, 2009. [ Links ]
[9] Califano, A. and Zaritzky, N. Simulation of freezing or thawing heat conduction in irregular two-dimensional domains by a boundary-fitted grid method, LWT - Food Sci Technol; 30, pp. 70-76, 1997. [ Links ]
[10] Kays, W. and Crawford, M., Convective heat and mass transfer, In: J.J. Morrison y J.M. Morriss (eds). McGraw- Hill, New York, USA. pp. 540-590, 1993. [ Links ]
[11] Choi, Y. and Okos, M., Effects of temperature and compositions on the thermal properties of foods. In: M. Le Maguer y P. Jelen (eds). New York: Elsevier. pp. 93-101. 1986. [ Links ]
[12] Patankar, S.V., Numerical Heat Transfer and Fluid Flow, Hemisphere, Washington, DC, USA. 1980. [ Links ]
[13] Lima, E., Silva, A., Silveira-Neto, A. and Damascenso, J., Numerical simulation of two-dimensional flows over a circular cylinder using the immersed boundary method, J Comput Physics; 189, pp. 351-370, 2003. [ Links ]
[14] Liang, C. Papadakis, G. and Luo, X., Effect of tube spacing on the vortex shedding characteristics of laminar flow past an inline tube array, Comput & Fluids; 38, pp. 950-964, 2009. [ Links ]
[15] Curcio, S., Aversa, M., Calabro, V. and Iorio, G., Simulation of food drying: FEM analysis and experimental validation, J Food Eng; 87, pp. 541-553, 2008. [ Links ]













