Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.170 Medellín dez. 2011
NUMERICAL SIMULATION OF THE INSTABILITY LINE BASED ON LAWS OF PHYSICS
SIMULACIÓN NUMÉRICA DE LA LÍNEA DE INESTABILIDAD BASADA EN LEYES DE LA FÍSICA
ALFONSO M. RAMOS
PhD. GeophysicalInstitute. Pontificia Universidad Javeriana. Bogotá, Colombia, a-ramos@javeriana.edu.co
JOSÉ E. ANDRADE
PhD.Department of Civil and Mechanical Engineering.California Institute of Technology. Pasadena, CA, USA, jandrade@caltech.edu.
ARCESIO LIZCANO
PhD.Department of Civil and Environmental Engineering.Universidad de Los Andes. Bogotá, Colombia, alizcano@uniandes.edu.co
Received for review July 13th, 2010, accepted May 2th, 2011, final version May , 5th, 2011
ABSTRACT:This work presents a numerical study of the instability line that relies on balance laws of physics rather than phenomenology. The instability line defines the onset of static liquefaction for loose sandy materials in the p-q space of effective stresses under undrained loading conditions. The onset of static liquefaction is predicted by means of a recently developed criterion and specialized to an elastoplastic constitutive model. The performance of this criterion is compared with laboratory tests showing satisfactory results. For a given void ratio and different mean pressures, it is found that the mobilized friction angle at the onset of static liquefaction is not constant. Therefore, the instability line is not an intrinsic property of the sand, but depends on the current state of the material. This work re-interprets the hypothesis given by VaidandChern, which has been amply used to analyze liquefaction phenomena.
KEYWORDS: liquefaction, instability, sand, elastoplasticity
RESUMEN: Este trabajo presenta un estudio numérico de la línea de inestabilidad basado en leyes de la física y no en fenomenología. La línea de inestabilidad muestra el momento en que se presenta licuación estática en arenas en el espacio de esfuerzos efectivos p-q bajo condiciones no drenadas. La línea de estabilidad se construyócon base en un criterio de inestabilidad recientemente formulado. Dicho criterio se especializó a un modelo constitutivo elastoplástico. La capacidad predictiva tanto del modelo como del criterio se compara con ensayos obteniendo resultados satisfactorios. Se encuentra que dada una relación de vacíos, el ángulo de fricción movilizado en licuación no es constante para diferentes confinamientos. De lo anterior se deduce que la línea de inestabilidad no es un parámetro de la arena, sino que es una variable dependiente del estado. Los resultados abren la puerta para reinterpretar la hipótesis deVaidy Chern ampliamente usada para analizar licuación.
PALABRAS CLAVE: licuación, inestabilidad, arena, elastoplasticidad
1. NTRODUCTION
The most common way of addressing problems associated with liquefaction in sands relies on phenomenology [1]. The generalization of the behavior of loose sands based on undrained triaxial tests has been widely used to understand static liquefaction[2,3,4]. However, generalization based on experimentation (i.e., phenomenology) is always limited by the quantity and quality of available laboratory tests. The instability line has been used to characterize the onset of liquefaction in saturated loose sands, not only in static conditions [2,3,4], but also in cyclic loading conditions [5]. This line can be defined in the p-q space of effective stresses as the limit where large strains are suddenly generated due to the inability of the soil element to sustain a given load or stress[6]. The concept of instability line was originally proposed by Vaid andChern [2]. They proposed the construction of the instability line by crossing a line through all the points that define liquefaction for a given void ratio and undrained monotonic loading.According to Vaid and Chern[2], these points define a straight line in p-q space of stress and correspond to the peak of deviatoric stress q. Conceptually, the most important aspect underlying the Vaidand Chern'sdefinition [2] is that the friction angle mobilized at the onset of static liquefaction is constant for a given void ratio, independent of additional aspects such as the confining pressure. This would indicate that the friction angle mobilized at the onset of liquefaction (i.e.,the slope of the instability line 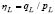 in the p-q space) is an intrinsic property of the material. Lade [7] proposed that the state of stress at which instability (static liquefaction) may occur corresponds to the top of the yield surface for a material whose behavior is simulated in the framework of non-associativeelastoplasticity with isotropic hardening in an undrained stress path. At this point, the second order plastic work ceases to be positive, and therefore theDrucker's stability postulate is violated [8].
in the p-q space) is an intrinsic property of the material. Lade [7] proposed that the state of stress at which instability (static liquefaction) may occur corresponds to the top of the yield surface for a material whose behavior is simulated in the framework of non-associativeelastoplasticity with isotropic hardening in an undrained stress path. At this point, the second order plastic work ceases to be positive, and therefore theDrucker's stability postulate is violated [8].
On the other side, Chu and Wanatowski [9] implicitly assume that sands can be simulated in the framework of elastoplasticity by an isotropic hardening yield surface. They state that the top of the yield surface is very close to the top of the undrained stress path in p-q space. Based on the aforementioned observation, they conclude that the instability line could be drawn by passing a line across all the points defining the peak point under undrained conditions, reinforcing the VaidandChernproposal. This procedure has been widely used for the interpretationand analysisof the onset of static liquefaction.
The literature reports two methodsfor the interpretation of laboratory tests. The first method relies on the result of one test where static liquefaction occurs.A straight instability line is drawn starting from the origin of coordinates in p-q space to the point that marks the onset of liquefaction[3,6]. It implies that the mobilized friction angle is constant independently of the mean pressure (Vaid&Chern's [2] hypothesis).
However, in this paper we show that the friction angle in the onset of liquefaction is not an intrinsic property of the material so that the instability line is not a straight line, but a curve in the p-q space of stresses. Moreover, it will show that if the critical state theory is accepted, the line of instability, either straight or curved, cannot depart from the origin of coordinates onthe p-q plane, as it has been reported by some authors [3,6,10].
The second method available for the construction of the instability line uses the onset of liquefaction from a test for different void ratios [3]. This contradicts the spirit of the instability line, which is to characterize the sand for specific initial conditions (i.e.,a void ratio).
In this work, a criterion proposed by Andrade [11], which isbased on laws of physics,is used to detect the onset of static liquefaction. The criterion is specialized to an elastoplastic constitutive model based on the bounding surface theory with kinematic hardening [12].The performance of both the constitutive model and the criterion of liquefaction were validated with laboratory tests. Once the simulations were validated, we proceeded to generate results for a wider range of initial conditions. Numerical simulations overcome the shortcomings of the experiments, (i.e., a limited number of results), and allow for us to havea wider spectrum of aspectsthat affect the sand in the onset of liquefaction.
Since we show that the friction angle mobilized at the onset of static liquefaction is not an intrinsic property of the material, the VaidandChernproposal [2] should be revised. For undrained tests of loose sands, the instability line is not a straight line but a curve. This means that the higher the confining pressure, the lower the friction angle mobilized in the onset of liquefaction. Furthermore, we show that for low mean pressures, the instability curve could be approximate to a straight line projected from the origin of coordinates on the p-q plane.
This paper is organized as follow: First, we briefly present the elastoplastic constitutive model, emphasizing relevant aspects that allow for one to capturethe stress-strain behavior. After that, the criterion for detecting the onset of liquefaction specialized for the elastoplastic constitutive model adopted in this work is presented. Subsequently, the performance of both the constitutive model and the criterion for the onset of static liquefaction is validated against laboratory tests. Then we obtain a mathematical expression for the stress ratio at the onset of liquefaction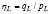 , which allows us to verify that this ratio is not constant, but depends on the state variables. Finally, a discussion and conclusions are given.
, which allows us to verify that this ratio is not constant, but depends on the state variables. Finally, a discussion and conclusions are given.
2. CONSTITUTIVE MODEL
The elastoplastic constitutive model adopted in this work is based on a kinematic hardening law for the yielding surface, along with the theory of bounding surface, framed on the theory of critical state [13]. These surfaces are combined with the state parameter 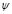 [14], which measures how far the material is from the critical state. The volumetric and shear elastic stiffness are functions of both the void ratio and the mean pressure. Dilatancy and peak stress ratio dependon
[14], which measures how far the material is from the critical state. The volumetric and shear elastic stiffness are functions of both the void ratio and the mean pressure. Dilatancy and peak stress ratio dependon 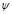 , which allows a single set of material parameters for a wide range of confining pressures and densities. The elastoplastic constitutive model encompasses a kinematic hardening law to describe the evolution of the yield surface and a bounding surface within the framework of the critical state theory. Interested readers can find a detailed description of the constitutive model in [13,15].
, which allows a single set of material parameters for a wide range of confining pressures and densities. The elastoplastic constitutive model encompasses a kinematic hardening law to describe the evolution of the yield surface and a bounding surface within the framework of the critical state theory. Interested readers can find a detailed description of the constitutive model in [13,15].
3. CRITERION FOR THE ONSET OF LIQUEFACTION
Recently, Andrade [11] developed a criterion for detecting the onset of liquefaction in a general elastoplastic framework with assumptions based on previous work by Borja[16]. The new criterion was derived in terms of the hardening modulus H, and it is based on Hill's theory of bifurcation [17] and laws of physics. Within the framework of elastoplasticity, the hardening modulus H can be obtained by resorting to the consistency condition:

where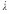 is the plastic multiplier,
is the plastic multiplier, 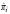 is the vector which contains the evolution laws for the internal variables
is the vector which contains the evolution laws for the internal variables 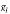 , and Fis the yield function. The hardening modulus reflects the state of the material. At the onset of liquefaction, the hardening modulus H reaches a critical value
, and Fis the yield function. The hardening modulus reflects the state of the material. At the onset of liquefaction, the hardening modulus H reaches a critical value 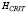 [11].
[11].
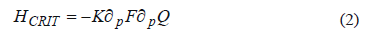
whereK is the elastic bulk modulus andQ is the plastic potential. Static liquefaction will occur when 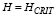 [11].
[11].
The critical hardening modulus for the constitutive model used in this work is given by [12]:
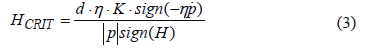
whered is the dilatancy function, η is the stress ratio q/p, and 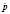 is the rate of the mean pressure p.
is the rate of the mean pressure p.
4. VALIDATION OF THE LIQUEFACTION CRITERION
The onset of static liquefaction based on the approach suggested in [11] has been successfully tested in [11-12]. This paper evaluates the performance of the criterion given by Eq. (3) for experimental results reported by [3] for Changi sand. Figure 1 depicts the stress ratio at the onset of liquefaction (i.e.,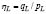 ) for five undrained triaxial tests on loose sand [3]. Two isotropic compression testswhose conditions were CU:(p0=150 kPa, q0=0 kPa, e=0.916); (p0=150 kPa, q0=0 kPa, e=0.888) and three anisotropic compression tests under a K0stress path K0U:(p0=191.22 kPa, q0=152.83 kPa, e=0.899); (p0=199.93 kPa, q0=183.28 kPa, e=0.881); (p0=199.57 kPa, q0=147.78 kPa, e=0.922). In addition, Fig. 1 shows the stress ratio at the onset of liquefaction (i.e.,
) for five undrained triaxial tests on loose sand [3]. Two isotropic compression testswhose conditions were CU:(p0=150 kPa, q0=0 kPa, e=0.916); (p0=150 kPa, q0=0 kPa, e=0.888) and three anisotropic compression tests under a K0stress path K0U:(p0=191.22 kPa, q0=152.83 kPa, e=0.899); (p0=199.93 kPa, q0=183.28 kPa, e=0.881); (p0=199.57 kPa, q0=147.78 kPa, e=0.922). In addition, Fig. 1 shows the stress ratio at the onset of liquefaction (i.e.,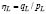 ) obtained from simulations based on the constitutive model described in Section 2 and the hardening modulus criteria given by Eq. 3. The constants of the constitutive model (Table 1) were calibrated using the experimental results reported in [4].
) obtained from simulations based on the constitutive model described in Section 2 and the hardening modulus criteria given by Eq. 3. The constants of the constitutive model (Table 1) were calibrated using the experimental results reported in [4].
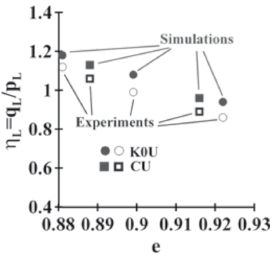
Figure 1. Stress ratio at the onset of static liquefaction in the experiments carried out by [3] and the simulations based on the constants given in Table 1
Table 1. Constants for Changi sand

When the sample has higher void ratios, the stress ratio at the onset of liquefaction is lower. Therefore, greater resistance is mobilized at the onset of liquefaction for denser materials thanfor loose sands. Figure 1 shows a reasonably good agreement between the experimental results and the simulations at the onset of liquefaction. Stress-induced anisotropy has a strong influence on the stress-strain behavior on granular materials under small deformation levels. The anisotropy of stresses is induced, for example, in K0 compression tests (Fig. 1, K0U). From the micromechanical point of view, the contact forces and contacts between the particles are oriented in the direction of the principal stresses.The preferred orientation of contact forces induces a stiffening of the sand's structure in a preferential direction[18]. This induced stiffness affects the behavior mainly before failure at low strain levels [18], thus the sand is affected at the onset of liquefaction by the induced anisotropy.
The constitutive model and the criterion of liquefaction used in this study (Eq. 3) are able to take into account the influence of small variations in void ratio (e = 0.888 and e = 0.881) in the stress ratio at the onset of liquefaction 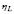 . This applies for both the isotropic and the anisotropic compression of the sample.
. This applies for both the isotropic and the anisotropic compression of the sample.
5. NUMERICAL SIMULATIONS
Once the constitutive model and the liquefaction criteria were validated against experiments conducted on Changi sand, simulations were performed for different pressures and void ratios. Results are shown in Fig. 2.
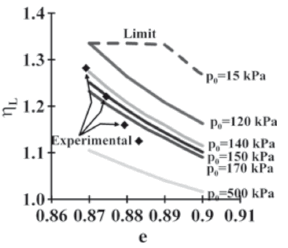
Figure 2. Stress ratio ηL versus void ratio for different confining pressures. The range of the initial mean pressure for the experimental data is between 150 to 200 kPa.
Figure 2 shows the results from simulations of a sample isotropically compressed before undrained shearing conditions were applied. The curves correspond to 6 different confining pressures and 4 units of experimental data are included for comparison. Figure 2 shows that for a given initial mean pressure, the looser the sand, the lower the stress ratio required to produce static liquefaction. On the other hand, for a given void ratio, the higher the initial mean pressure of the sample, the lower the stress ratio ηL. This means that the friction angle mobilized at the onset of static liquefaction varies with the mean pressure. The friction is lower at higher confining pressures.This shows that ηL is not an intrinsic property of the sand, as originally proposed by VaidandChern [2] and also adopted in later works[3,9,10].
After a few lines of derivation, we obtain a mathematical expression for the stress ratio in liquefaction for the constitutive model used in this study:
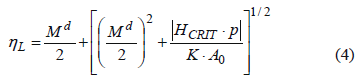
whereMd is defined as 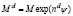 . A0, nd, and M are constants of the sand (Table 1).
. A0, nd, and M are constants of the sand (Table 1).
We can conclude that the stress ratio ηLshould not be interpreted as a constant of the material. Equation 4 shows that ηL depends on the critical hardening modulus which in turn depends on the state variables. A similar result was found by [11] for an isotropic elastoplastic constitutive model with two invariants.
Wanatowskiand Chu [3] presented a line connecting the experimental points of Fig. 2. However, each experiment corresponds to a different mean pressure. This means that a curve joining the experimental points would be crossed by curves of constant confining pressure, as shown in Fig. 2.
Figure 2 shows a dashed line called limit. This upper limit indicates that, given a void ratio, it is not possible to indefinitely decrease the mean pressure in order to reach a higher stress ratio ηL.The upper limit is given by the lower mean pressure that a sample can sustain for developing static liquefaction. Thus, undrained triaxial tests with mean pressures lower than the upper limit will display strain hardening behavior.
The curve for mean pressure p0=15 kPa which is part of the limit curve is shown. This curve also separates the static liquefaction behavior of strain hardening for the range of void ratios considered.
The limit of Fig. 2 is framed in the critical state of the sand and can be explained by the state parameterψ =e-ec[14]. The valueyis a measure of the distance between the current void ratio and the void ratio ata critical state for the same mean pressure. For materials exhibiting strain hardening behavior,y is greater than zero. On the other hand, ay less than zero is characteristic of a material that is susceptible to suffer static liquefaction. Let's suppose that there is a material with a void ratio and mean pressure such that y is greater than zero.As the mean pressure decreases, y decreases as well. If the mean pressure is low enough, y may have negative values. That causes the behavior of the material to change from contractive to dilatants. Therefore, the sand will not tend to generate static liquefaction.
The upper limit curve shown in Fig.2 sets a maximum value for the stress ratio that is close to 1.35, which is the slope of the critical state M (Table 1). This means that for low values of mean pressure, the stress ratio at liquefaction (i.e.,ηL) is located very close to the critical state line M.The critical state line arises from the origin of coordinates in the p-q plane.The aforementioned aspects may indicate that the line of instability arises from the coordinate origin in p-q plane. However, as explained by the limits presented in Fig. 2, the behavior of static liquefaction is limited by a certain value of mean pressure greater than zero that varies for each type of material. Therefore, the instability line might begin as a projection from the origin for small values of mean pressure, but never has a locus in the origin of the p-q plane.
Figure 3 shows the critical state line and the instability line with void ratio e = 0.89 for Changi sand. This curve can be constructed easily from the data of Fig. 2 by doing a vertical cross section at void ratio e = 0.89. Also, a box near the origin of coordinates is shown, whose data are zoomed in Fig. 4.
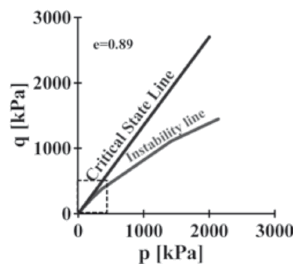
Figure 3. Critical state line and instability line for Changi sand, e=0.89
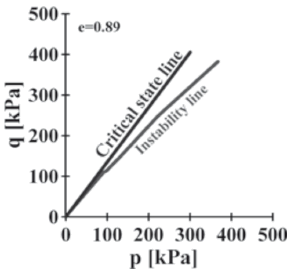
Figure 4. Critical state line and instability line for the Changi sand close to the origin of coordinates, e=0.89
As indicated by Eq.4, the instability line is not straight, as proposed by [2], but is a curve. A close up nearby to the origin of coordinates of Fig. 3 is shown in Fig. 4.
The mobilized friction angle changes for each level of mean pressure. An inspection of Fig. 3 and Fig. 4 confirm the previous statement. As a consequence, the instability line is not a straight but a curve. However, for low levels of mean pressure the variation of the angle is not significant for Changi sand.
An interpretation of undrained triaxial tests on loose sand for low mean pressures will result on an instability curve which can be approximated by a straight line with no significant implications in the practice of engineering. However, conceptually, it is not correct. In addition, one can state that for low levels of stresses, the instability line can be projected from the origin despite the fact that the instability line cannot be part of the origin of coordinates on the p-q space of stresses.
It is important to mention that the analysis presented here does not contradict the experimental results reported by some authors [3,4,6,10]. On the contrary, this analysis explains them satisfactorily-basedon a criterion for liquefaction that relies on the laws of physics-and it allows us to generalize the behavior of loose sand under undrained conditions of loading by means of numerical simulations. The aforementioned experimental results assumed Vaid and Chern's hypothesis [2] to betrue.The hypothesis that the friction angle mobilized at the onset of liquefaction is constant relies on the interpretation of a limited number of experiments (phenomenology), and they attempted to generalize those results. The stresses used by [3,4,6,10] are in the range where the instability curve can be approximated as linear.
Furthermore, a straight line of instability has been used to define the onset of flow liquefaction under cyclic loading conditions [5,20].However, others have shown that the stress path in undrained tests on loose sand can cross the instability line and no signal of liquefaction is seen [19].
Ramos et al. [12] showed that the criterion of critical hardening (Eq.3) can successfully detect the onset of liquefaction under cyclic conditions for laboratory tests, reinforcing the fact that the mobilized friction angle is not anintrinsic property of the material.
6. CONCLUSIONS
Simulations of the onset of static liquefaction based on laws of physics are presented here. The study overcomes some of the shortcomings of phenomenology to generalize the behavior of loose sand under undrained loadingconditions. This approach can help to predicting the instable mechanical behavior of sandy soils in deep foundations, like those presented in alluvial fans [21]
The instability line is not a straight line but a curve for a given void ratio. This means that the mobilized friction angle at the onset of liquefaction is not a material constant.
This analysis generalizes the results of static undrained triaxial tests on loose sand presented by different authors on Changi sand and suggests that the VaidandChern hypothesis related to the mobilization of a constant friction angle at the onset of liquefaction is only valid for low confining pressures. For higher confining pressures, the mobilized friction angle decreases.
Conceptually, an error occurs when the instability line is supposed to be straight. However in practical terms, this simplification does not have major implications for low values of mean pressure inChangi sand.
REFERENCES
[1] Youd et al., Liquefaction resistance of soils: Summary report from the NCEER and 1998 NCEER/NSF workshop on evaluation of liquefaction resistance of soils. Journal of Geotechnical and Geoenvironmental Engineering. Vol. 127(10), pp. 817-833. 2001. [ Links ]
[2] Vaid, Y. P., Chern, J. C., Cyclic and monotonic undrained response of saturated sands. In: Advances in the art of testing soils under cyclic conditions ASCE. Pp. 120 -147.1985. [ Links ]
[3] Wanatowski, D., Chu, J., Static liquefaction of sand in plane strain. Canadian Geotechnical Journal.Vol 44, pp. 299-313.2007 [ Links ]
[4] Leong, W., Chu, J.,Teh, I., Liquefaction and instability of a granular fill. Geotechnical Testing Journal.Vol 23 (2), pp. 178-192. 2000 [ Links ]
[5] Vaid, Y. P., Sivathayalan, S.,Fundamental factors affecting liquefaction susceptibility of sands. Canadian Geotechnical Journal.Vol 37 (3), pp. 592-606. 2000 [ Links ]
[6] Chu, J., Leroueil, S., Leong, W. Instable behaviour of sand and its implication for slope instability. Canadian Geotechnical Journal.Vol 40, pp. 873-885. 2003 [ Links ]
[7] Lade, P. V., Instability and liquefaction of granular materials. Computers and Geotechnics.Vol 16 (2), pp. 123-151. 1994 [ Links ]
[8] Drucker, D. C., A definition of stable inelastic material. Journal of applied mechanics.Vol 26, pp. 101-106. 1959. [ Links ]
[9] Chu, J.,Wanatowski, D., Instability conditions of loose sand in plane strain. Journal of Geotechnical and Geoenvironmental Engineering. Vol 134 (1), pp. 136-142. 2003 [ Links ]
[10] Hyodo, M., Tanimizu, H., Yasufuko, N., Murata H., 1994. Undrained cyclic and monotonic triaxialbehaviour of saturated loose sand.Soils and Foundations.Vol 34 (1), pp. 19-32. 1994. [ Links ]
[11] ANDRADE, J. E. A predictive framework for liquefaction instability.Geotechnique.Vol 59( 8), pp. 673-682. 2009 [ Links ]
[12] Ramos, A. M., Andrade, J. E., Lizcano, A.,Instability criterion for flow liquefaction under cyclic loading. To be submitted.2010 [ Links ]
[13] Dafalias, Y. F.,Manzari, M. T.,Simple plasticity sand model accounting for fabric change effects. Journal of Engineering mechanics. Vol 130 (6), pp. 622-633.2004. [ Links ]
[14] Been, K., Jefferies, M. G., 1985. A state parameter for sands.Geotechnique.Vol 35 ( 2), pp. 99-112. 1985 [ Links ]
[15] Manzari, M. T.,Dafalias, Y. F., A critical state two-surface plasticity model for sands. GeotechniqueVol 47 (2), pp. 255 -2 272. 1997. [ Links ]
[16] Borja, R. I., Condition for liquefaction instability in fluid-saturated granular soils. ActaGeotechnica.Vol 1 (4), pp. 211-244. 2006. [ Links ]
[17] Hill, R., A general theory of uniqueness and stability in elastic-plastic solids. Journal of the Mechanics and Physics of Solids.Vol 6(39), pp. 236-249.1958. [ Links ]
[18] Gajo, A., Piffer, L., de Polo, F., Analysis of certain factors affecting the unstable behavior of saturated loose sand. Mechanics of cohesive-frictional materials.Vol5, pp. 215-236. 2000. [ Links ]
[19] Alarcon-Guzman, A., Leonards, A., Chameau, L.,Undrained monotonic and cyclic strength of sands. Journal of Geotechnical Engineering.Vol114 (10), 1988. [ Links ]
[20] Kramer, S., Geotechnical Earthquake Engineering. Prentice Hall International Series. New Jersey. 1996. [ Links ]
[21] Gaviria, C., Gómez, D., Thomson, P., Evaluación de la integridad de cimentaciones profundas: Análisis y verificación in situ. DYNA. Año 76 No 159, pp. 23-33. 2009. [ Links ]














