Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.170 Medellín dez. 2011
DEGREDATION PROPERTIES OF REINFORCED CONCRETE WALLS WITH OPENINGS
PROPIEDADES DE DEGRADACIÓN DE MUROS DE CONCRETO REFORZADO CON ABERTURAS
JULIAN CARRILLO
Ph D, Assistant Professor, Universidad Militar Nueva Granada, Bogotá, Colombia, & Research Assistant, Universidad Nacional Autónoma de México, wcarrillo@umng.edu.co
SERGIO ALCOCER
Ph D, Research Professor, Instituto de Ingeniería, Universidad Nacional Autónoma de México, salcocerm@ii.unam.mx
Received for review: June 15th, 2010; accepted: May 9th, 2011; final version: May 10th, 2011
ABSTRACT: This paper compares the performance of four isolated reinforced concrete (RC) walls with openings: two prototype walls tested under quasi-static cyclic (QSC) loading, and two models tested under shaking table excitation. The variables studied were the web steel ratio, the type of web reinforcement, and the testing method. By means of the measured response, it was verified that loading history of the QSC testing ignores the foremost dynamic effects observed in structures subjected to earthquake loads. When dynamic and QSC responses were compared, it was apparent that stiffness and strength degradation properties depend on the loading rate, the strength mechanisms associated to the failure modes, number of cycles, and cumulative parameters such as ductility demand and energy dissipated. We deducted that data obtained from QSC tests cannot always be safely assumed to be a lower limit of the expected capacity. Stiffness and strength degradation models for RC walls with openings subjected to earthquake-type loading are also proposed.
KEYWORDS: degradation, stiffness, strength, concrete walls, openings, shaking table testing
RESUMEN: En este artículo se compara el comportamiento de cuatro muros aislados de concreto reforzado (CR) con aberturas: dos muros prototipo ensayados bajo carga cuasi-estática cíclica (CEC) y dos muros ensayados bajo excitación de mesa vibratoria. Las variables estudiadas fueron la cuantía de acero en el alma, el tipo de acero de refuerzo en el alma y el método de ensaye. A partir de la respuesta medida se verificó que la historia de carga de los ensayos CEC ignora los efectos dinámicos fundamentales observados en estructuras sometidas a cargas sísmicas. Cuando las respuestas dinámicas y CEC cíclicas se compararon, se observó que las propiedades de degradación de rigidez y resistencia dependen de la velocidad de aplicación de carga, los mecanismos de resistencia asociados a los modos de falla, el número de ciclos y los parámetros acumulados de la demanda de ductilidad y energía disipada. Por lo tanto, los datos obtenidos a partir de ensayos CEC no siempre se pueden suponer de forma segura como un límite inferior de la capacidad esperada. En el artículo también se proponen modelos de degradación de rigidez y resistencia para muros de CR con aberturas sometidos a carga del tipo sísmica.
PALABRAS CLAVE: Degradación, rigidez, resistencia, muros de concreto, aberturas, ensayo en mesa vibratoria.
1. INTRODUCTION
While quasi-static (QS) tests are the simplest to perform, they are also the most limited for providing information on the true dynamic behavior of test specimens. In general, the loading history of the QS method ignores many dynamic effects observed in real structures subjected to earthquake loads, mainly, the strain rate effects (Calvi et al., 1996). As a result, when the seismic behavior of an element or system is studied using the QS method, imprecise interpretations of results can be generated, mostly in the following cases (Leon & Deierlein, 1996; Rai, 2001; Carrillo & González, 2007; Mosalam et al., 2008): a) when the governing failure mode is strongly affected by the strain rates, b) when the material that controls the behavior is brittle, such as concrete and masonry; c) when the overstrength characteristics are a fundamental issue on the response, and d) when the ductility and energy dissipation capacities are important parameters. Thus, it is unclear whether the data obtained from QS tests can be safely assumed to be a lower bound for strength, ductility, and energy dissipation capacity. For instance, the effect of the strain rate on degrading materials (i.e., concrete, masonry) on structural performance has not been adequately studied (Leon & Deierlein, 1996). According to Rai (2001), neglecting the effect of strain rates in QS testing gives rise to many of its unique strengths as a testing method; i.e., the ability to detect and observe damage propagation, as well as the ability to provide a consistent basis for comparison among test programs.
In order to study the seismic behavior of RC walls for housing, a large research program has been underway between the Instituto de Ingenieria at the UNAM and Grupo CEMEX. The experimental program has included QSC tests and dynamic loading tests of RC walls with different height-to-width ratios (Carrillo & Alcocer, 2008) and walls with openings (door and window).
Aimed at studying stiffness and strength degradation properties, the behavior of four isolated shear walls with two openings is compared in this paper. Two full-scale prototype walls were tested under QSC loading and two lightly scaled models were tested under shaking table excitation. The experimental response was studied in order to identify the main parameters affecting the strength and stiffness degradations during dynamic and QSC testing. The performance of walls was compared by using the failure modes, hysteresis curves, loading rates, number of cycles, and the cumulative parameters-such as ductility demand and energy dissipated.
2. EXPERIMENTAL PROGRAM
The three-dimensional prototype is a two-story RC house with shear walls in the two main directions. Typically, wall thickness and clear height are 100 and 2400 mm, respectively. Nominal compressive strength is 15 MPa. In the experimental program, four isolated walls with openings were studied: two full-scale prototypes tested under QSC loading and two 1:1.25 scaled models tested under shaking table excitation. Because the size of the models was very similar to the prototypes, the simple law of similitude was chosen. According to this law of similitude, the models are built with the same material as the prototype (i.e., the properties of materials are not changed) and only the dimensions of the models are altered.
2.1 Geometry and reinforcement
The variables studied were the web steel ratio (0.125 % and 0.25 %) and the type of web reinforcement (deformed bars and welded wire meshes). The geometry and the reinforcement layout of the models tested under shaking table excitation are illustrated in Fig. 1. The wall models were built on a foundation beam bolted to the platform of the shaking table. The thickness of the models was 80 mm. The areas of door and window openings were equivalent to 32% of the wall area. Longitudinal and transverse reinforcement at the boundary elements were the same in both specimens: 4 No. 4 longitudinal deformed bars (12.7 mm diameter = 4/8 in.) and No. 2 smooth bar stirrups (6.4 mm diameter = 2/8 in.) at 180-mm spacing. This reinforcement was designed in order to prevent flexural failure. Specimen MVN100D was reinforced for web shear with a single layer of No. 3 vertical and horizontal deformed bars (9.5 mm diameter = 3/8 in.) with spacing of 320 mm. The amount of web reinforcement corresponds approximately to the minimum web steel ratio prescribed by the ACI-318 (2008) building code, which is equal to 0.25 % [Fig. 1(b)]. Specimen MVN50mD was reinforced for web shear with a single mesh (6x6-8/8) of No. 8 wires (4.1 mm diameter) with a spacing of 150 mm (~6 in.). The web steel ratio was approximately 50% of the minimum ratio prescribed by ACI-318 [Fig. 1(a)]. This test was aimed at examining the performance of walls reinforced with a steel percentage smaller than the minimum prescribed by the code. A lower steel ratio is supported by the fact that lower concrete compressive strength and higher yield strength for the web steel require, in theory, smaller percentages than the 0.25 % minimum prescribed ratio. Prototype walls (MVN100C and MVN50mC) were tested under QSC loading.
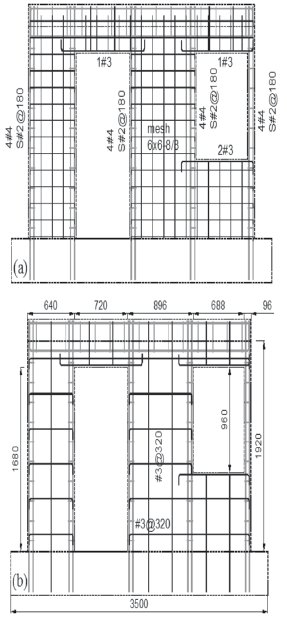
Figure 1. Geometry and reinforcement layout of models: a) MVN50mD, b) MVN100D
2.2 Mechanical properties of materials
For design purposes, nominal concrete compressive strength was 15 MPa, and nominal yield strength of bars and wire reinforcement were 412 MPa (mild steel) and 491 MPa (cold-drawn wire reinforcement), respectively. The mean value of the measured compressive strength was 24.7 MPa for prototype walls, and 16.0 MPa for wall models. The mean value of the measured yield strength of No. 3 (9.5 mm diameter) bars and wire reinforcement (4.1 mm diameter) were 435 MPa and 630 MPa, respectively. For concrete, properties were obtained at the time of testing.
2.3 Loading histories
Aimed at studying wall performance under different limit states, from the onset of cracking to collapse, models were subjected to three earthquake hazard levels using both natural and artificial acceleration records. An earthquake record from an epicentral region in Mexico (Mw = 7.1, CA-71), was used for the seismic demand in the elastic limit state. The earthquake was recorded at the Caleta de Campos station on January 11, 1997. This record was considered to be a Green function (basic event) to numerically simulate larger-magnitude events, i.e. with larger instrumental intensity and duration (Ordaz et al., 1995). Two earthquakes with Mw magnitudes 7.7 (CA-77) and 8.3 (CA-83) were numerically simulated in order to represent the strength and ultimate limit states, respectively. Time history accelerations for prototype walls are presented in Fig. 2. According to the law of similitude, acceleration and time scale factors were applied to these records for testing the models. Models were tested under progressively more severe earthquake actions, which were scaled up considering the value of peak acceleration as the reference factor, until the final damage stage was attained.
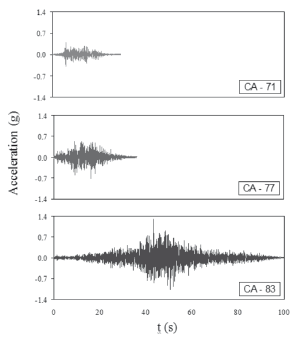
Figure 2. Loading histories for dynamic testing
Isolated models were designed taking the fundamental period of vibration of the prototype house into consideration. In order to establish such dynamic characteristic, analytical models were developed and calibrated through ambient vibration testing. The fundamental period of vibration of the two-story house was estimated at 0.12 s (Carrillo & Alcocer, 2008). Taking into account the scale factor for period quantity of simple law of similitude, ST = 1.25, isolated wall models were designed to achieve an initial in-plane vibration period (Te), close to 0.10 s (0.12s/1.25). For design purposes, it was supposed that walls would behave as a single degree of freedom system. The dynamic weight, Wd (mass × gravity acceleration) necessary to achieve the desired design period Te, was calculated as (KeTe2/4p2)g; where Ke is the in-plane stiffness of the wall that was calculated from the measured mechanical properties of the materials. To account for premature shrinkage cracking, the moment of inertia of the wall section was reduced by 25%. As a result, the dynamic weight was 188.2 kN.
In QSC testing, the loading protocol consisted of a series of increasing amplitude cycles. For each increment, two cycles of the same amplitude were applied (I and II). The first two cycles were applied to reach 25 % of the calculated cracking load (Load 1). In the next increment (Load 2), 50 % of the calculated cracking load was reached. Afterwards, an increment to attain the actual cracking load (Load 3) was applied. After that, the loading history was controlled by drift ratio using increments with an amplitude equal to 0.002. A typical loading history during QSC testing in terms of displacement measured at mid-thickness of the top slab and the effective time between steps is depicted in Fig. 3.
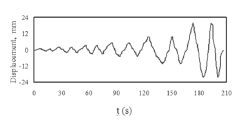
Figure 3. Typical loading histories for QSC testing
2.4 Test setups and instrumentation
In dynamic testing, models were subjected to a series of base excitations represented by the selected earthquake records. Records were reproduced by a shaking table where the foundation beam of the models was bolted. If the dynamic weight were to rest at the top of models, the risk of lateral instability would have been a major concern. Then, an alternative method for supporting the mass and transmitting the inertia forces was required. An external device for a mass-carrying load system that is allowed to slide horizontally on a fixed supporting structure located outside the shaking table was designed (see Fig. 4, Carrillo & Alcocer, 2011). In QSC testing, the lateral loads were applied directly at the top slab level through double-action hydraulic actuators (see Fig. 5). An axial compressive stress of 0.25 MPa, which roughly corresponds to 2 % of the nominal concrete compressive strength, was applied on top of the walls. The axial load was kept constant during testing. In dynamic testing, it was exerted through the weight of the load and connection beams, as well as lead ingots that were bolted to the load beam. Although lead ingots resulted in a triangular load distribution, the addition of the weight of the connection beam makes for a uniform distribution of the axial load on the walls. In QSC testing, the axial load was achieved using a lever system arranged by a weight hung at side walls, which caused the vertical force on the load beam.
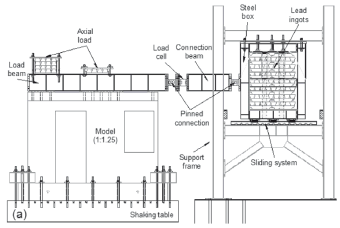
Figure 4. Test setup for shaking table testing
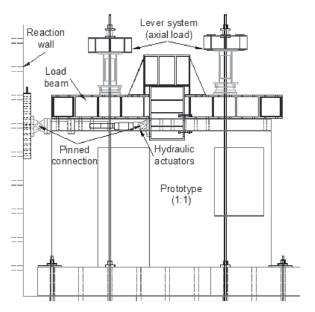
Figure 5. Test setup for QSC testing
To measure the specimens' response, walls were instrumented internally and externally. Internal instrumentation was designed to acquire data on the local response of reinforcement through strain-gages bonded to the steel reinforcement. External instrumentation was planned in such a way that we would be able to learn about the global response through displacement, acceleration and load transducers. Also, an optical displacement measurement system [with Light Emitting Diodes (LEDs]] was used. In the tests, 59 strain-gages and 64 external transducers were used (Carrillo, 2010).
3. TEST RESULTS
The experimental response was studied in order to identify the main parameters affecting the strength and stiffness degradations during dynamic and QSC testing. Initially, the overall performance of walls was compared by using failure modes and hysteresis curves. Then, detailed behavior was assessed through the loading rate, number of cycles, and the cumulative parameters-such as ductility demand and energy dissipated (Carrillo, 2010).
3.1 Crack patterns and failure modes
In dynamic testing, walls reinforced with welded wire mesh and with 50 % of the minimum code prescribed steel ratio exhibited diagonal tension (DT) failures. The failure mode was governed by a plastic yielding of reinforcement and a subsequent fracture of the wires. Failure was brittle because of the limited deformation capacity of the wire mesh itself. In contrast, walls reinforced with deformed bars and with 100 % of the minimum steel ratio exhibited a mixed failure mode, where diagonal tension and diagonal compression, DT-DC (i.e., the yielding of some reinforcing bars in the web and noticeable crushing of concrete), was observed (see Fig. 6). Although walls tested under QSC loading exhibited comparable failure modes and cracking patterns, the number and length of the cracks was larger than in the walls tested under dynamic loading. The differences are related mainly with the strain rate. When marking cracks during QSC testing, it was not uncommon to observe crack propagation of some cracks while maintaining peak load. It is evident that this type of crack propagation could not have occurred in a short time interval during dynamic testing.
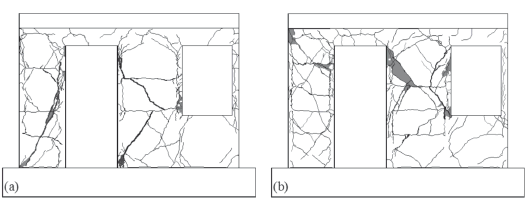
Figure 6. Final crack patterns in dynamic testing: a) MVN50md, b) MVN100D
3.2 Hysteresis curves
The hysteresis curves were expressed in terms of the normalized shear strength, V/Vnormal and ductility demand. The shear strength predicted using equations proposed by Carrillo et al. (2009a), Vnormal, was utilized to normalize the measured lateral force, V. Predicted shear strength was calculated using measured wall dimensions and the mechanical properties of materials. The ductility demand was calculated by dividing the drift ratio (R) by a conventional yield drift ratio (Ry), corresponding to the development of 80% of the peak strength (Park, 1988). The drift ratio, R, was obtained by dividing the relative displacement measured at the mid-thickness of the top slab, by the height at which such displacement was measured. The envelopes of the hysteresis curves and the failure mode are shown in Fig. 7. According to the loading history, two envelopes for QSC testing are drawn: using the data associated with the first (I) and second (II) cycle of each increment (see Fig. 3).
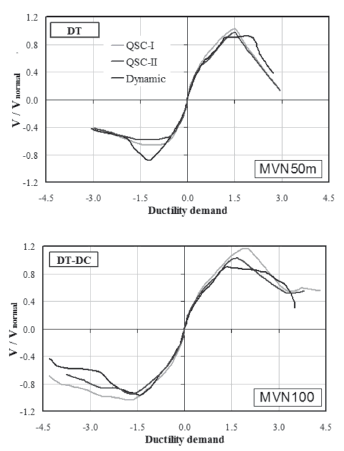
Figure 7. Envelopes of hysteresis curves
As expected, differences were observed between the general performance of the specimens tested using real dynamic actions and the specimens tested under QSC loading. The foremost differences are associated with the shear strength capacity. For example, in specimen MVN50m, which failed due to diagonal tension, the dynamic envelope was slightly higher than the QSC envelope associated with the second cycle (QSC-II). Moreover, the dynamic envelope was associated with a more ductile response. In contrast, in specimen MVN100, which exhibited a mixed failure, the two envelopes (dynamic and QSC-II) were, in general, comparable.
4. STIFFNESS AND STRENGTH DEGRADTION
Stiffness and strength degradation properties were studied by means of observed parameters, that is, loading rate, strength mechanisms associated to the failure modes, number of cycles, and cumulative parameters such as ductility demand and energy dissipated.
4.1 Loading rate
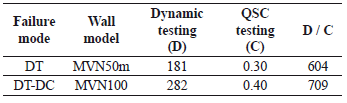
The effect of the loading rate on the structural behavior is widely recognized (Calvi et al., 1996; Leon & Deierlein, 1996; Rai, 2001; Mosalam et al., 2008). However, rate effects on RC shear walls have not yet been clearly quantified. Measured maximum loading rates in terms of displacement (mm/s) are shown in Table 1. Velocities were calculated by dividing the relative displacement measured at the mid-thickness of the top slab by the time step. In dynamic testing, the later corresponds to the constant time step of the records (0.01 s). In QSC testing, the effective time between steps was used (Fig. 3). The ratio between the maximum velocities measured during dynamic (mean value) and QSC testing is included in Table 1. Such a ratio is approximately equal to 650. Therefore, the loading rates are noticeably different between the two methods of testing. The observed higher shear strength in dynamic testing of specimen with DT failure would be associated with the loading rate effect.
Table 1. Measured loading rates during testing (mm/s)
4.2 Cumulative parameters
For dynamic and QSC testing, the ductility demand and the maximum number of equivalent cycles at a certain range of ductility (Nmax) were calculated. The symbol Nmax represents the maximum value of the ratios between the cumulative energy dissipated in a cycle and the cumulative energy dissipated associated with the range of ductility. Data is plotted in Fig. 8, where fitted regression curves are also shown. The fitted curves show a very good correlation with test data as can be observed from the correlation coefficient, r (Benjamin & Cornell, 1970).
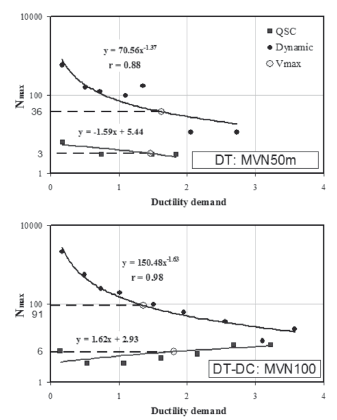
Figure 8. Variation of the maximum number of equivalent cycles
Observing Fig. 8, it is apparent that at a certain value of ductility demand, Nmax was different between the two groups of specimens (DT and DT-DC failures). Thus, for the purpose of comparison, the ductility demand at shear strength (Vmax) was used. This point is depicted in Fig. 8. It is evident from Fig. 8, that Nmax is very different between dynamic and QSC testing. For example, in QSC testing, Nmax at Vmax was equal to 3 and 6 in specimens with DT and DT-CD failure modes, respectively. However, in dynamic testing these values were 36 and 91 in specimens with DT and DT-CD failure modes, respectively. As mentioned earlier, in the specimen with DT failure, shear strength capacity in dynamic testing was higher than in the QSC testing. However, in dynamic testing, Nmax at Vmax was approximately 12 times (36/3) higher than in the QSC testing. In the specimen with DT-CD failure mode, shear strength capacity in dynamic testing was just slightly lower than that in QSC testing, but the difference in Nmax was more remarkable, about 15 times (91/6) higher. Therefore, the number of cycles is a key parameter to be used for explaining the differences between the observed behaviors.
The cumulative energy dissipated and the cumulative ductility demand are shown in Fig. 9. The energy dissipated in a cycle is the area within the hysteresis loop enclosed by the shear force-relative displacement curve. To remove the scale factors in QSC results, the yield shear strength (Vy = 0.8Vmax) times yield drift ratio (Ry) was used to normalize the cumulative energy dissipated (Ecum/VyRy).
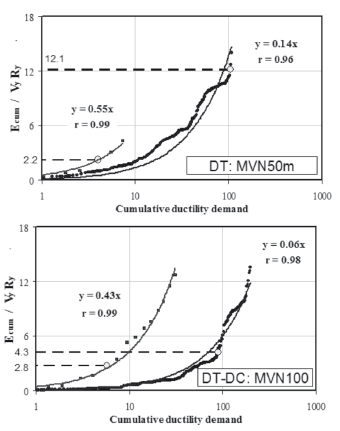
Figure 9. Variation of the cumulative energy dissipated
In dynamic testing, the cumulative energy dissipated at shear strength (Vmax) was clearly different between specimens MVN50m and MVN100. For example, normalized cumulative energy dissipated was equal to 12.1 and 4.3 in specimens MVN50m and MVN100, respectively. The observed variations in the cumulative energy dissipated are essentially related to the effect of the number of cycles on the strength mechanisms, which, in turn is associated with different failure modes. For instance, when the failure mode is related to the cracking or/and crushing of concrete (i.e., DT-DC failures), stiffness and strength degradation rates increase noticeably as the number of cycles augment. Also, the pinching of hysteresis loops becomes more significant. Consequently, the hysteresis loops are narrower and, thus, the energy dissipated is reduced. In contrast, when the failure mode is governed by the plastic yielding of reinforcement and its subsequent fracture (i.e., DT failures), the number of cycles slightly affects the stiffness and strength properties. In QSC testing, the normalized cumulative energy dissipated at Vmax was higher in the specimen with DT-DC failure than in the specimen with DT failure (2.8 versus 2.2, see Fig. 9); i.e., the effect of the number of cycles on the cracking or/and crushing of concrete was not observed.
4.3 Degradation models
Aimed at establishing a stiffness degradation model by using the dynamic response and also aimed at numerically correlating the dynamic and QSC strength degradation, measured cumulative parameters were studied. Ductility demand (m), cumulative ductility demand (mcum), cycle stiffness (K), the ratio between K and initial stiffness (K/Ko), the ratio between dynamic and QSC normalized strength (V/VQSC), energy dissipated (E), cumulative energy dissipated (Ecum), and the number of equivalent cycles at a certain value of ductility demand (N), were calculated for each loading cycle for both types of tests. It was observed that the failure mode did not significantly affect the stiffness degradation. The type of concrete and the geometry of the wall are the main parameters affecting stiffness behavior (Carrillo, 2010). Therefore, test data for the two specimens tested under dynamic loading and for some values of N are plotted in Fig. 10. In contrast, it was observed that strength degradation is remarkably influenced by the failure mode, i.e., the crushing of concrete or the plastic yielding of steel reinforcement. After that, test data for specimens with DT failure mode and for specimens with DT-DC failure mode are plotted in Figs. 11-a and 11-b, respectively. Fitted nonlinear regression curves are included in Figs. 10 and 11. In this study, two commonly used measures for the "goodness-of-fit" of the results of the nonlinear regression analyses were computed: the correlation coefficient (r) and the standard error of the residuals (SE). As shown in Figs. 10 and 11, the fitted curves showed a very good agreement with the test data, as can be observed from r (close to one) and EE (close to zero).
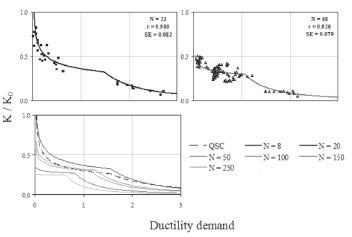
Figure 10. Stiffness degradation
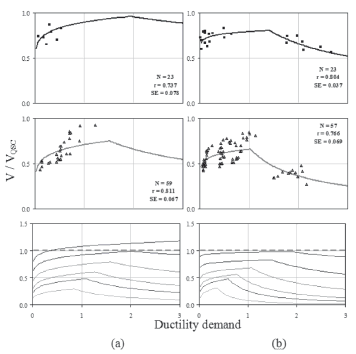
Figure 11. Strength degradation: a) DT failure, b) DT-DC failure
Following the trends from the experimental results, stiffness and strength degradation could be divided into two branches (see Fig. 12). For the stiffness degradation curve (K/K0), the degradation rate of the second branch was larger than that of the first branch. For strength degradation (V/VQSC), the first branch includes the pinching of the dynamic hysteresis loops regarding the QSC hysteresis envelope.
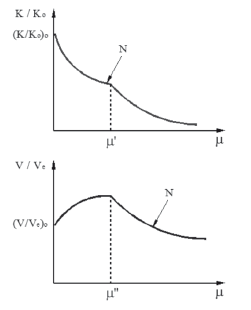
Figure 12. Degradation models: stiffness (K/K0) and strength (V/Ve)
Evaluating trends from the experimental results (see Figs. 10 and 11) and performing an iterative nonlinear regression analysis, empirical equations depicted in Table 2 are proposed for estimating the stiffness and strength degradation properties for RC walls with openings. The regression analysis and the investigation of existing trends between residuals (prediction errors) and model parameters helped in order to improve the forms of the equations.
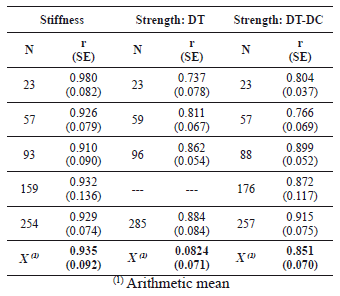
Computed measures of the "goodness-of-fit" of the results of the nonlinear regression analyses are shown in Table 3. It can be seen that the correlation between observed degradation parameters (K/K0 and V/Ve) and those computed with proposed equations (Table 2) are very good and that the standard errors of the residuals are relatively small.
Table 3. Computed measures of "goodness-of-fit"
Stiffness and strength degradation curves were calculated by using the model equations (see Table 2). Results for the same value of N are depicted in the last row of Figs. 10 and 11. QSC results are included in these curves. As shown in Fig. 10, when N is equal to or lower than 20, dynamic stiffness is larger than that measured under QSC testing. As expected, when the failure mode is governed by concrete crushing, strength degradation was considerably apparent (see Fig. 11). Also, when N is equal to or lower than 8, and the failure mode is governed by the plastic yielding of reinforcement, dynamic strength was higher than QSC strength.
5. CONCLUSIONS
Results of an experimental study of RC shear walls with openings subjected to dynamic and QSC loading were presented and discussed. Shaking table tests were shown to be essential not only for assessing the dynamic characteristics of specimens, but also for verifying QSC test results. It was confirmed that the loading history of the QSC testing ignored the principal dynamic effects observed in structures subjected to earthquake loads, mainly, the parameter associated with the strain rate and the number of cycles. When the dynamic and QSC responses were compared, stiffness and strength degradation properties were clearly dependent upon the loading rate, the strength mechanisms associated to the failure modes (crushing of concrete or plastic yielding of reinforcement), the number of cycles, as well as the cumulative parameters such as ductility demand and energy dissipated. It was found that data obtained from QSC tests cannot always be safely assumed to be a lower limit of the performance capacity of RC shear walls with openings subjected to earthquake-type loading. According to the computed measures of the "goodness-of-fit" of the results, the proposed empirical models can be used suitably in order to predict the stiffness and strength degradation properties for RC walls with openings.
REFERENCES
[1] ACI COMMITTEE 318. Building code requirements for structural concrete (ACI-318-08) and commentary (ACI-318R-08). Farmington Hills, Michigan, 2008. [ Links ]
[2] Benjamin, J. and Cornell C., Probability, statistics and decision for civil engineers. McGraw-Hill, New York, 1970. [ Links ]
[3] Calvi, G., Kingsley, G. and Magenes, G., Testing of masonry structures for seismic assessment. Journal of Earthquake Spectra: 12 (1), pp. 145-163, 1996. [ Links ]
[4] Carrillo, J., Evaluation of shear behavior of concrete walls for housing using dynamic testing. Ph.D Thesis, National University of Mexico, UNAM (In Spanish), 2010. [ Links ]
[5] Carrillo, J. and Alcocer, S., Improved external device for a mass-carrying sliding system for shaking table testing. Journal of Earthquake Engineering and Structural Dynamics: 40 (4), pp. 393-411, 2011. [ Links ]
[6] Carrillo, J. and Alcocer, S., Shaking table tests of low-rise concrete walls for housing. Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, Paper 12-01-11, 2008. [ Links ]
[7] Carrillo, J. and González, G., Inelastic modeling of concrete frames with nonreinforced masonry. DYNA Journal: 74 (152), pp. 229-239 (In Spanish), 2007. [ Links ]
[8] Carrillo, J., Alcocer, S. and Uribe R., Prediction of shear performance of concrete walls for housing. Proceedings of XVII National Conference on Earthquake Engineering, Mexico, Section V, Paper 02 (In Spanish), 2008a. [ Links ]
[9] Leon, R. and Deierlein, G., Considerations for the use of quasi-static testing. Journal of Earthquake Spectra: 12 (1), pp. 87-109, 1996. [ Links ]
[10] Mosalam, K., Hagerman, J. and Kelly, H., Seismic evaluation of structural insulated panels. Proceedings of the 5th International Engineering and Construction Conference, ASCE (IECC'5), Los Angeles, California, 2008. [ Links ]
[11] Ordaz, M., Arboleda, J. and Singh S., A scheme of random summation of an empirical Green's function to estimate ground motions from future large earthquakes. Bulletin of the Seismological Society of America: 85 (6), pp. 1635-1647, 1995. [ Links ]
[12] Park R., Ductility evaluation for laboratory and analytical testing. Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, Vol. 8, pp. 605-616, 1988. [ Links ]
[13] RAI D. Slow cyclic testing for evaluation of seismic performance of structural components. Journal of Earthquake Technology: 38 (1), 31-35, 2001. [ Links ]















