Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.170 Medellín dez. 2011
INFLUENCE OF RAINFALL INTENSITY ON INFILTRATION AND DEFORMATION OF UNSATURATED SOIL SLOPES
INFLUENCIA DE LA INTENSIDAD DE LA LLUVIA EN LA INFILTRACION Y DEFORMACION DE TALUDES PARCIALMENTE SATURADOS
EDWIN FABIAN GARCIA ARISTIZABAL
Doctor en Ingeniería, Facultad de Ingeniería, Escuela Ambiental, Universidad de Antioquia, profesor asistente, egarcia@udea.edu.co
CARLOS ALBERTO RIVEROS JEREZ
Doctor en Ingeniería, Facultad de Ingeniería, Escuela Ambiental, Universidad de Antioquia, profesor asistente, riveros@udea.edu.co
MANUEL ALONSO BUILES BRAND
Master en Ingeniería, Universidad de Medellín, docente e investigador, mabuiles@udem.edu.co
Received for review November 3th, 2010, accepted March 11th, 2011, final version March, 23th, 2011
ABSTRACT: In order to improve the understanding of the influence of rainfall intensity on infiltration and deformation behavior of unsaturated soil slopes, numerical 2D analyses are carried out by a three-phase elasto-viscoplastic seepage-deformation coupled method. From the numerical results, it is shown that regardless of the saturated permeability of the soil slope, the increase in the pore water pressure (reduction in suction) during rainfall infiltration is localized close to the slope surface. In addition, the generation of the pore water pressure and the lateral displacement are mainly controlled by the ratio of the rainfall intensity to the saturated permeability of the soil.
KEYWORDS: unsaturated soil, slope stability, rainfall infiltration, numerical analysis
RESUMEN: Con el objeto de entender más claramente la influencia de la intensidad de la lluvia en el proceso de infiltración y deformación de taludes en suelos parcialmente saturados, se han realizado análisis numéricos en 2D usando un método trifásico acoplado que incluye un modelo elasto-viscoplástico. Los resultados numéricos muestran que independientemente de la permeabilidad saturada del talud, el incremento en la presión de poros (reducción de la succión) durante la infiltración de la lluvia se localiza cerca a la superficie del talud. Adicionalmente, los incrementos en la presión de poros y en los desplazamientos laterales son controlados pincipalmente por la relación entre la intensidad de la lluvia y la permeabilidad saturada del suelo.
PALABRAS CLAVE: suelo parcialmente saturado, estabilidad de taludes, infiltración de lluvias, análisis numérico
1. INTRODUCTIONN
The failure of unsaturated slopes is a common phenomenon all over the world. Although it can be attributed to many factors, such as geology, topography, hydrological conditions, material properties, and human action; it has been widely recognized that water infiltration has a dominant effect on slope instability. Many researchers have reported on embankment and slope failure due to rainfall infiltration (e.g., [1-7]). Failure of soil structures can be triggered by a wetting process (e.g., both short and long infiltration caused by rainfall or melting snow) from an unsaturated state, as a result of the increase of the moisture content and the reduction of suction. This, in turn, leads to a decrease in the shear strength of the soil and the development of deformations. The study of rainfall infiltration-deformation behavior on unsaturated soils is very complex because it is controlled by many variables associated to the non-linear hydraulic and constitutive properties of the soil, as well as the characteristics of the rainfall. Therefore, rainfall infiltration becomes an interesting subject due to the necessity of understanding its effects on the increase of the pore water pressure and the generation of deformation in unsaturated slopes.
Some studies have addressed the effect of rainfall infiltration on the slope stability from the point of view of the statistical approach (e.g., [8,9]). On the other hand, several researchers have been implementing numerical solutions to analyze the effect of the hydraulic characteristics on the instability of unsaturated slopes (e.g., [10-13]). In these formulations, the effects of the rainfall infiltration on the generation of pore water pressure and on slope stability are generally evaluated by a seepage analysis using the finite element method followed by slope stability analysis; thus, the study of the coupling of deformation and transient flow is disregarded. However, the deformation behavior of unsaturated soil is strongly dependent on seepage flow and vice versa. Accordingly, rainfall infiltration-deformation problems are better formulated by the use of coupled seepage-deformation methods.
Numerical methods that can simultaneously consider unsaturated seepage flow and the deformation of soil structures have been used to study the infiltration process [6,14-16]. Although the seepage-deformation coupled methods have become more popular for the study of unsaturated seepage flow; the particular case of the rainfall infiltration problem and its effects on the development of deformations in unsaturated slopes has not yet been fully addressed or understood.
In this paper, a multiphase coupled elasto-viscoplastic finite element formulation proposed by Oka et al. [17] is used to describe the rainfall infiltration process and its effect on the development of pore water pressure and deformation into an unsaturated slope. A significant feature of the numerical method addressed here, is the use of a coupled seepage-deformation model which allows for the calculation of the displacements along with the reduction of suction or increase of pore water pressure. The numerical analysis is based on the porous media theory (e.g., [18]). The materials are assumed to be composed of solid, water, and gas phases, which are assumed to be continuously distributed throughout space on the macroscopic level. An elasto-viscoplastic constitutive model is adopted for the soil skeleton. The skeleton stress, which is determined from the difference between the total stress and the average pore fluid pressure, is used for the stress variable in the constitutive model. In addition, the effect of suction is expressed as the shrinkage or the expansion of the overconsolidation (OC) boundary surface and the static yield surface [17].
A numerical analysis, which focuses on a parametric study including different rainfall intensities and saturated water permeabilities, is carried out to observe the influence of these hydraulic characteristics on the changes of pore water pressure and the progress of the lateral displacements during rainfall infiltration into unsaturated slopes.
2. GOVERNING EQUATIONS
2.1 Skeleton stress
Terzaghi [19] defined the concept of a stress tensor for water-saturated materials. In the case of unsaturated soils, however, the concept needs to be redefined in order to consider compressible materials. In the present formulation, skeleton stress s´ij is defined and then used for the stress variable in the constitutive relation for the soil skeleton. Total stress tensor sij is obtained as the sum of the partial stresses, namely,
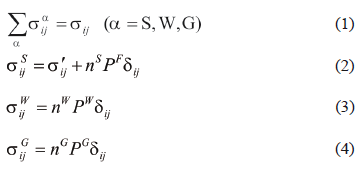
where PW and PG are the pore water pressure and the pore air pressure, respectively, n is the porosity, na is the volume fraction of phase a (a = S:Solid, W:Water, G:Air), and PF is the average pore pressure calculated according to saturation s, which is given through Dalton's law as follows:

From Eqs. (1) to (5) we have,

The skeleton stress is used as the basic stress variable in the model for unsaturated soils.
2.2 Conservation of mass
The conservation of mass is given by the following equation:
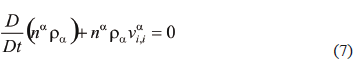
in which D/Dt denotes the material time derivative, ra is the material density, and via is the velocity of the a phase. Assuming that the particles and water are incompressible, the conservation laws for water and air phases are expressed as functions of s and n, that is
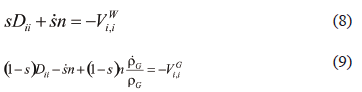
where Dii is the volumetric stretching and Via is the apparent velocity of phase a.
2.3 Equilibrium equation
The rate type of equilibrium equation is expressed as follows:

in which 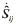 is the nominal stress rate tensor. The above incremental equilibrium equation is used for the updated Lagrangian formulation of the boundary value problem.
is the nominal stress rate tensor. The above incremental equilibrium equation is used for the updated Lagrangian formulation of the boundary value problem.
2.4 Soil water characteristic curve
The relation between saturation and suction is given by the equation proposed by van Genuchten [20].
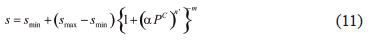
in which a, n´, and m are fitting parameters that describe the shape of the soil water characteristic curve, and the relation m = 1-1/n´ is assumed, smax and smin are the maximum and the minimum limiting values of saturation, respectively.
The effects of the degree of saturation on permeability for water and air are assumed as:

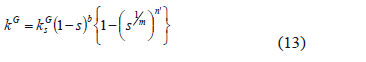
where a and b are material parameters, ksW is the coefficient of permeability for water under saturated conditions and ksG is the coefficient of permeability for air under fully dry conditions.
2.5 Elasto-viscoplastic model for unsaturated soil
An elasto-viscoplastic model based on the overstress-type of viscoplastic theory with soil structure degradation for saturated soil [21] has been extended to unsaturated soil using the skeleton stress and the suction effect in the constitutive model [17]. In this model it is assumed that there is an overconsolidation boundary that delineates the normally consolidated (NC) region, fb ≥ 0, and the overconsolidated region (OC), fb < 0, it is described as follows:
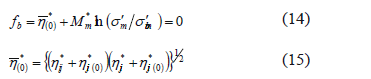
where 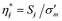 , Sij is the deviatoric stress tensor, s'm is the mean skeleton stress, Mm* is the value of
, Sij is the deviatoric stress tensor, s'm is the mean skeleton stress, Mm* is the value of 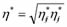 when the volumetric strain increment changes from contraction to dilation, which is equal to Mf* at the critical state. The strain-hardening parameter s'mb controls the size of the boundary surface. The suction effect on the unsaturated soil is incorporated as:
when the volumetric strain increment changes from contraction to dilation, which is equal to Mf* at the critical state. The strain-hardening parameter s'mb controls the size of the boundary surface. The suction effect on the unsaturated soil is incorporated as:
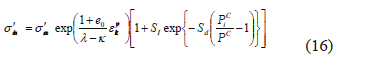
where 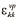 is the viscoplastic volumetric strain, l and k are the compression and the swelling indexes, respectively, and e0 is the initial void ratio. Different parameters are used to include the suction effect: PiC is the initial suction value, PC is the present suction value, SI is the material parameter that denotes the strength increment when suction is PiC, and Sd is the parameter which controls the rate of increasing or decreasing strength. Finally, s'ma is a strain-softening parameter used to describe the degradation of the material caused by structural changes.
is the viscoplastic volumetric strain, l and k are the compression and the swelling indexes, respectively, and e0 is the initial void ratio. Different parameters are used to include the suction effect: PiC is the initial suction value, PC is the present suction value, SI is the material parameter that denotes the strength increment when suction is PiC, and Sd is the parameter which controls the rate of increasing or decreasing strength. Finally, s'ma is a strain-softening parameter used to describe the degradation of the material caused by structural changes.
The static yield function is given by:
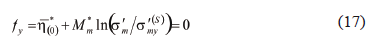
Similarly, onto the overconsolidation boundary surface, the suction effect is introduced in the value s'my(S) as
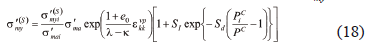
The viscoplastic stretching tensor is given by the following equation which is based on Perzyna's type of viscoplastic theory as

in which fp is the viscoplastic potential surface, F1 denotes a material function for rate sensitivity, Cijkl is the viscoplastic parameter.
More details about the formulation can be found in Garcia et al. [22].
3. NUMERICAL ANALYSIS
The multiphase seepage-deformation coupled method including the elasto-viscoplastic model for unsaturated soil described in Section 2 is used to simulate the rainfall infiltration into the unsaturated slopes. In this formulation, an updated Lagrangian method with the objective Jaumann rate of Cauchy stress is adopted [17]. The independent variables are the pore water pressure, the pore air pressure, and the nodal velocity. In the finite element formulation, an 8-node quadrilateral element with a reduced Gaussian integration is used for the displacement, and 4 nodes are used for the pore water pressure and the pore air pressure. The backward finite difference method is used for the time discretization.
3.1 Boundary conditions
The finite element mesh and the boundary conditions for the simulation of the rainfall infiltration into the unsaturated slopes are shown in Fig. 1. The mesh is denser close to the surface where the high hydraulic gradients due to the rainfall infiltration and seepage flow are expected. For displacement, the slope is fixed at the bottom in both horizontal and vertical directions; the lateral boundaries are fixed only in a horizontal direction.
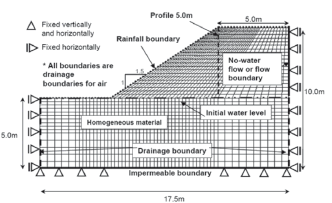
Figure 1. FE mesh and boundary conditions
The initial negative pore water pressure (suction) distribution is considered to be linear. The water level in the soil is assumed to be located at 5.0 m, measured from the bottom impermeable boundary. The flux of air is allowed for the entire boundaries and the initial air pressure is assumed to be zero. The boundary conditions for water flux are described in this manner: an impermeable boundary is assigned to the bottom or soil foundation; for the lateral sides of the slope below the water level the boundary is considered to be permeable; and above the water level the boundary is initially impermeable, but it changes to be permeable if the pore water pressure turns positive; the toe, the slope surface and the crest of the slope are assumed to be rainfall boundaries.
Assuming that there is always water available on the soil surface due to the rainfall, at the initial stage of the infiltration, the unsaturated soil has enough space to allow all the water to infiltrate into the soil; however, once the soil surface is saturated, ponding occurs and the excess of water either accumulates on the surface or dissipates as runoff. Two different boundaries are used to simulate this kind of "dyna-normal">Flow boundary. If the rainfall intensity is smaller or equal to the saturated water permeability and the saturation of the surface is smaller than the maximum saturation, i.e., I < = ksW and ssurface < smax, a prescribed flow boundary is used and all the water infiltrates into the soil.
- If the rainfall intensity is larger than the saturated water permeability, and the saturation of the surface is equal to the maximum saturation; i.e., I > ksW and ssurface = smax, a pore water pressure boundary is prescribed on the surface; in this case, the incoming of water within the soil is controlled by the gradient of the matric suction. The pore water pressure assigned on the surface is calculated according to the rainfall intensity. In the simulation, it is assumed that the excess water is dissipated as runoff.
3.2 Material parameters and simulation cases
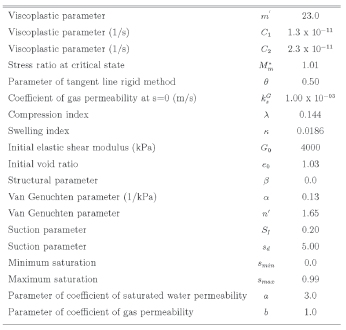
The material parameters required by the constitutive model described in Section 2 are listed in Table 1. In order to study the effect of the rainfall intensity and the saturated water permeability on the infiltration and deformation behavior of the unsaturated soil slopes, different combinations of rainfall patterns and saturated water permeabilities are chosen for the simulations and they are shown in Table 2. The horizontal permeability is considered to be 10 times the vertical permeability.
Table 1. Material parameters of the soil
The rainfall patterns used for the analysis are shown in Fig. 2. The rainfall pattern R-1 corresponds to the rainfall pattern recommended by the Japan Institute of Construction Engineering [23] for the seepage analysis of river embankments. This rainfall pattern consists of two different minor and major rainfalls; the minor rainfall event of 200 mm total rainfall is distributed evenly over a period of time equal to 200 h (I = 1.00 mm/h), and a major rainfall event of 300 mm total is distributed evenly over a period of time equal to 30 h (I = 10.00 mm/h). In rainfall patterns R-2 and R-3, the major rainfall is distributed evenly along smaller periods of time (R-2: 15 h, R-3: 5 h, respectively), which leads to higher rainfall intensities (R-2: I = 20.00 mm/h, R-3: I = 60.00 mm/h, respectively).

Figure 2. Rainfall intensities for the analyses
4. NUMERICAL RESULTS
The distribution of saturation corresponding to the rainfall pattern R-1, the saturated water permeability ksvW = ksW = 1.0x10-6 m/s, and for the rainfall infiltration times t = 100 h, and 230 h are shown in Fig. 3. Figure 3 shows that when the rainfall is applied, the saturation of the slope increases notably in depths relatively close to the soil surface, and gradually the wetting front progresses inside the slope when the time increases. For time t = 100 h, when the rainfall intensity is smaller than the saturated water permeability, I < ksvW, the soil above the water level remains unsaturated and the wetting front reaches a maximum saturation about 0.70. At the time t = 200 h, the major rainfall starts to be applied on the slope surface (I = 10.00 mm/h) for a total period of time t = 30 h. In this case, the rainfall intensity is larger than the saturated water permeability of the soil, I > ksvW; the surface of the slope starts to saturate, as well as the depth of saturation increases with the advancing of time due to the sufficient amount of water provided on the slope surface.
Figure 3. Distribution of saturation (t = 100h, 230 h)
4.1 Pore water pressure profiles
Figure 4(a) presents the comparison of the pore water pressure profiles for the different water saturated permeabilities used for the simulations, namely, ksvW = ksW, 2ksW, 5ksW, and 10ksW, at the end of the rainfall 1 (R-1), with maximum rainfall intensity I = 10 mm/h (2.78 x 10-6 m/s), and for a rainfall infiltration time equal to 230 h.
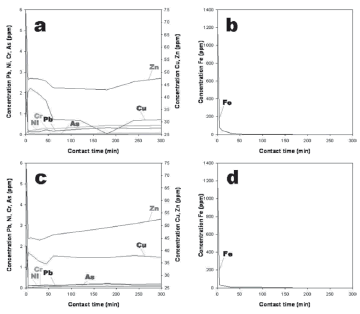
Figure 4. Pore water pressure profiles for different rainfall intensities and permeabilities
Figure 4(a) shows different responses in the pore water pressure distributions along the selected profile below the crest of the slope (as shown in Fig. 1). In the cases when the rainfall intensity is larger than the permeabilities of the soil, i.e., I = 2.78 x 10-6 m/s > 2ksW = 2.00 x 10-6 m/s > ksW = 1.00 x 10-6 m/s, the pore water pressures on the slope surface reach a value equal to zero. On the contrary, for the cases when the rainfall intensity is smaller than the permeabilities of the soil, I = 2.78 x 10-6 m/s < 5ksW = 5.00 x 10-6 m/s < 10ksW = 1.00 x 10-5 m/s, the slope surface remains unsaturated (negative pore water pressure); the higher the saturated water permeability, the smaller the pore water pressure developed on the surface.
During the infiltration process, if the saturated water permeability of the soil is smaller than the intensity of the rainfall, the infiltration capacity of the soil is exceeded and only a certain amount of water infiltrates into the soil; the excess of water accumulates on the surface or dissipates freely as runoff, which causes the surface of the slope to remain saturated. However, if the rainfall intensity is smaller than the saturated water permeability of the soil, the infiltration capacity of the soil is larger than the rainfall intensity, all the water infiltrates the soil and no accumulation or excess of water appears on the surface, maintaining the slope surface unsaturated.
Figure 4(a) also shows an additional considerable difference in the pore water pressure results obtained for the different saturated water permeabilities. The pore water pressures are larger at shallow depths for the permeabilities that are smaller than the rainfall intensity; and the pore water pressures are smaller for the cases when the permeabilities are larger than the rainfall intensity, between z = 10.0 m and 8.5 m. Nevertheless, when the depth increases, between z = 8.5 m and 6.5 m, this behavior is inverted and the pore water pressure becomes larger for the permeabilities that are larger than the rainfall intensity.
The previous results can be explained in terms of the saturated water permeability. In the case of soil with low permeability, although the surface remains saturated during rainfall, the water cannot be drained down quickly toward the water table; as a consequence, the pore water pressure develops closer to the slope surface. In contrast, for the high permeable soil the water does not accumulate on the surface and it can be drained down faster toward the water table, increasing the depth of the wetting front, as well as the pore water pressures at greater depths.
The results of the pore water pressure profiles obtained for rainfalls 2 and 3 (R-2 and R-3), with maximum rainfall intensities I = 20 mm/h and I = 60 mm/h and for rainfall infiltration times equal to 215 and 205 h, are shown in Figs. 4(b) and 4(c), respectively. All of the characteristics described above for the rainfall infiltration process into unsaturated slopes with different permeabilities are also obtained for these two different rainfall patterns. In the case of rainfall 3 (R-3), where the intensity I = 60 mm/hr is larger than the four permeabilities used in the simulations, the pore water pressure at the slope surface becomes zero for all the simulated cases.
A comparison of Figs. 4(a) to 4(c) shows that, regardless of the permeability, the increase of the pore water pressures due to the rainfall infiltration at shallow depths is more important than the increase of the pore water pressures at greater depths. This means that the rainfall patterns (different rainfall intensities and rainfall durations) have a more significant effect on the development of pore water pressures (reduction of suction) at shallow depths than at greater depths. This result is consistent with Au's [5] conclusion on the report of many soil failures during rainstorms in Hong Kong, that one of the most prominent ways by which the rainfall affects the instability of slopes is by the loss of pore water suction at shallow depths, which induces shallow and small slope failures. Similarly, rainfall-induced shallow landslides triggered by rainfall infiltration in Japan have also been reported by Yamagishi et al. [2].
4.1 Lateral displacement profiles
The influence of the rainfall intensity on the deformation of the unsaturated slopes during the infiltration process is estimated by the comparison of the lateral displacement at the end of the three rainfall infiltrations and below the crest of the slope. Firstly, the effect of the saturated permeabilities, namely, ksvW = ksW, 2ksW, 5ksW, and 10ksW, on the lateral displacement of the unsaturated slope is shown in Fig. 5(a) for rainfall 1 (R-1).
Figure 5. Lateral displacement profiles for different rainfall intensities and permeabilities
In Fig. 5(a), the maximum lateral displacements are obtained for the saturated water permeability ksvW = 2ksW = 2.00 x 10-6 m/s. This result suggests that for a given saturated water permeability, there is a critical rainfall intensity which leads to maximum deformation. In this case, the permeability value is the closest value to the applied rainfall intensity (I = 10 mm/hr = 2.78 x 10-6 m/s). The computed displacements are small, in the order of a few millimeters. The displacement profile along depth shows that the motion of the slope reduces when the depth increases. Similarly, Figs. 5(b) and 5(c) show the lateral displacement profiles for the cases of rainfalls 2 and 3 (R-2 and R-3), respectively. In these figures, the maximum lateral displacements are obtained for the saturated permeabilities ksvW = 5ksW = 5.00 x 10-6 m/s and ksvW = 10ksW = 1.00 x 10-5 m/s, respectively. These permeabilities are also the closest to the applied rainfall intensities (I = 20 mm/hr = 5.56 x 10-6 m/s and I = 60 mm/hr = 1.67 x 10-5 m/s, respectively); which confirm that for a given saturated water permeability, there is a critical rainfall intensity that develops the largest lateral deformations. As shown by Figs. 5(a) to 5(c), the rainfall intensity has a significant influence on slope deformation.
Zhan and Ng [24] pointed out a similar observation about the critical rainfall intensity, indicating that the critical rainfall infiltration rate which leads to the largest total increase of pore water pressure may be close to the saturated permeability of the soil. However, in the analysis presented by Zhan and Ng [24], the deformation behavior of the soil was not investigated. Alonso et al. [6] studied the rainfall infiltration process in an unsaturated layered slope composed of overconsolidated clays and found that there is a combination of saturated water permeabilities that lead to larger pore water pressures for a given rainfall record.
The simulation results suggest that higher permeabilities allow faster infiltrations along the soil profile inducing larger pore water pressures (reduction in suction); therefore, larger deformations are obtained through the slope, as shown in Fig. 5.
5. CONCLUSIONS
A multiphase elasto-viscoplastic FE formulation based on the theory of porous media was used to describe the rainfall infiltration process into an unsaturated soil slope. Numerical analyses were focused on the effects of rainfall distributions and the saturated water permeabilities on the development of pore water pressure and deformations. By using the numerical results, the effect of the rainfall infiltration on the deformation of unsaturated slopes was addressed. The calculated deformations were associated with the volume change of the soils as saturation increases during the rainfall infiltration.
The simulation results showed that larger pore water pressures are obtained at shallow depths when rainfall intensities are larger than saturated water permeabilities; in contrast, in the case of rainfall intensities smaller than the permeabilities, the pore water pressures at the surface are smaller. This behavior is inverted when the depth of the soil increases; at larger depths, the pore water pressures are larger for the soils with larger permeabilities. The analysis of the deformations showed that the maximum lateral displacements are obtained in the cases where rainfall intensity is closer to the saturated water permeability; i.e., I/ksW ≈ 1.0. The ratio of rainfall intensity to saturated water permeability is a fundamental property in the deformation response of unsaturated soils subjected to rainfall infiltration.
ACKNOWLEDGMENTS
The first author would like to thank Prof. Fusao Oka of Kyoto University for his constant support and advice during the development of this research.
REFERENCES
[1] Yoshida, Y., Kuwano, J. and Kuwano, R. Rain-induced slope failures caused by reduction in soil strength, Soils Found, 31(4), pp. 187-193, 1991. [ Links ]
[2] Yamagishi, H., Horimatsu, T., Kanno, T. and Hatamoto, M., Recent landslides in Niigata Region, Japan, Proceeding of the 4th Asian Symposium on Engineering Geology and the Environment. Hong Kong, 6, P. 2004. [ Links ]
[3] Nakata, Y., Liu, D., Hyodo, M., Yoshimoto, N. and Kato, Y., Numerical simulation of an expressway embankment slope failure, Unsaturated Soils, Theoretical and Numerical Advances in Unsaturated Soil Mechanics. Newcastle, Australia, pp. 719-724, 2010. [ Links ]
[4] Chen, H., Dadson, S. and Chi, Y., Recent rainfall-induced landslides and debris flow in northern Taiwan, Geomorphology, 77, pp. 112-125, 2006. [ Links ]
[5] AU, S. Rainfall-induced slope instability in Hong Kong, Eng. Geol., 51, pp. 1-36, 1998. [ Links ]
[6] Alonso, E., Gens, A., and Delahaye, C., Influence of rainfall on the deformation and stability of a slope in overconsolidated clays: a case study, Hydrogeol. J., 11, pp. 174-192, 2003. [ Links ]
[7] Garcia, E., and Uchimura, T., Estudio del mecanismo de falla de terraplenes debido a la infiltración de aguas lluvias mediante el monitoreo de presiones de poros y contenidos de agua, Dyna, 152, pp. 125-135, 2007. [ Links ]
[8] Au, S., Rainfall and slope failure in Hong Kong, Eng. Geol., 36, pp.141-147, 1993. [ Links ]
[9] Okada, K. and Sugiyama, T., A risk estimation method of railway embankment collapse due to heavy rainfall, Struct. Saf., 14, 131-150, 1994. [ Links ]
[10] Ng, C., and Shi, Q., A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage, Comput. Geotech., 22(1), pp. 1-28, 1998. [ Links ]
[11] Tsaparas, I., Rahardjo, H., Toll, D., and Leong, E., Controlling parameters for rainfall-induced landslides, Comput. Geotech., 29, pp. 1-27, 2002. [ Links ]
[12] Cai, F. and Ugai, K., Numerical analysis of rainfall effects on slope stability, Int. J. Geomech., 4(2), pp.69-78, 2004. [ Links ]
[13] Rahardjo, H., Ong, T., Rezaur, R. and Leong, E., Numerical analysis of rainfall effects on slope stability, Int. J. Geotech. Geoenv. Eng., 133(12), pp. 1532-1543, 2007. [ Links ]
[14] Cho, S. and Lee, S., Instability of unsaturated soil slopes due to infiltration, Comput. Geotech., 28, pp.185-208, 2001. [ Links ]
[15] Ehlers, W., Graf. T. and Amman, M., Deformation and localization analysis of partially saturated soil, Comput. Meth. Appl. Mech. Eng., 193, pp. 2885-2910, 2004. [ Links ]
[16] Oka, F., Kimoto, S., Takada, N. and Higo, Y., A multi-phase elasto-viscoplastic analysis of an unsaturated river embankment associated with seepage flow, Proceedings of the International Symposium on Prediction and Simulation Methods for Geohazard Mitigation. Kyoto, Japan, pp.127-132, 2009. [ Links ]
[17] Oka, F., Kodaka, T., Kimoto, S., Kim, Y., and Yamasaki, N., An elasto-viscoplastic model and multiphase coupled FE analysis for unsaturated soil, Proceedings of the Fourth International Conference on Unsaturated Soils. Carefree, USA, pp. 124-131, 2006. [ Links ]
[18] Boer, R., Theory of porous media - past and present, Z. Angew. Math. Mech., 78(7), pp. 441-466, 1998. [ Links ]
[19] Terzaghi, K., Theoretical Soil Mechanics, Wiley, 1943. [ Links ]
[20] VAN GENUCHTEN, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Am. J., 44, pp. 892-898, 1980. [ Links ]
[21] Kimoto, S. and Oka, F., An elasto-viscoplastic model for clay considering destructuralization and consolidation analysis of unstable behavior, Soils Found., 45(2), pp. 29-42, 2005. [ Links ]
[22] Garcia, E., Oka, F. and Kimoto, S., Numerical analysis of a one-dimensional infiltration problem in unsaturated soil by a seepage-deformation coupled method, Int. J. numer. Anal. Methods Geomech., 35(5), pp.544-568, 2011. [ Links ]
[23] JICE. Guide for structure investigations of river embankments, Japan Institute of Construction Engineering, 2002. [ Links ]
[24] Zhang, L. and NG, C., Analytical analysis of rainfall infiltration in unsaturated soils, Int. J. Geomech., 4, pp. 273-284, 2004. [ Links ]















