Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.170 Medellín dez. 2011
MODELING OF AN OSCILLATORY FREELY-ROTATING CUTTING BRUSH FOR STREET SWEEPING
MODELADO DE UN CEPILLO OSCILATORIO PARA BARRIDO DE CALLES EN ROTACIÓN LIBRE
LIBARDO V. VANEGAS-USECHE
Ph.D., Professor, Facultad de Ingeniería Mecánica, Universidad Tecnológica de Pereira, Pereira, Colombia, lvanegas@utp.edu.co
MAGD M. ABDEL-WAHAB
Ph.D., Professor, Department of Mechanical Construction and Production, Faculty of Engineering, Ghent University, B-9000 Gent, Belgium, Magd.AbdelWahab@UGent.be
GRAHAM A. PARKER
Ph.D., Professor, Faculty of Engineering and Physical Sciences, University of Surrey, Guildford, Surrey GU2 7XH, UK, G.Parker@surrey.ac.uk
Received for review July 21th, 2010, accepted March 14th, 2011, final version March, 31th, 2011
ABSTRACT: A dynamic model of a novel oscillatory cutting brush for street sweeping in free rotation is developed. The bristles are modelled as cantilever beams. The equation of motion is determined through the theory of forced transverse vibrations of beams, and the solution is based on the normal-mode method. A sinusoidal angular speed function and a novel function, named VAP, are studied. The model is validated through finite element analyses. The effects of brush parameters on brush dynamics are identified. Notably, for the VAP function, a condition similar to resonance tends to occur in the stronger plane for bending deflections, when the frequency of the brush is an odd fraction of a natural frequency of the bristle for that plane. The model can also be applied to study the dynamics of a small-deflection cantilever beam, when the transverse external force is a squared, sinusoidal, triangle, or VAP wave.
KEYWORDS: Gutter brush, small deflection, transverse vibrations, resonance
RESUMEN: Se desarrolla un modelo matemático de un cepillo lateral oscilatorio para barrido de calles en rotación libre. Las cerdas se modelan como vigas empotradas. La ecuación de movimiento se obtiene mediante la teoría de vibraciones forzadas de vigas, y la solución se basa en el método de modo normal. Se estudia una función sinusoidal y una novedosa función, llamada VAP. El modelo se valida mediante análisis de elementos finitos. Se identifican los efectos de los parámetros del cepillo sobre su dinámica. Para la función VAP, una condición similar a resonancia tiende a ocurrir en el plano fuerte para las deflexiones, cuando la frecuencia del cepillo es una fracción impar de una frecuencia natural de la cerda en dicho plano. El modelo sirve para estudiar las deflexiones pequeñas de una viga empotrada, sometida a vibraciones producidas por una onda sinusoidal, cuadrada, triangular o VAP.
PALABRAS CLAVE: Cepillo lateral, deflexiones pequeñas, vibraciones transversales, resonancia
1. INTRODUCTION
Street sweepers usually have a small brush that sweeps the debris that lies in the gutter. As about 80 % of the debris is found there [1], the operation of the gutter brush is crucial. Usually, it comprises steel wire bristles of rectangular cross section, arranged into one or more rows of clusters, forming an inverted cup. These brushes may be classified as cutting and flicking brushes, whose bristles deflect mainly in the radial and the tangential direction of the brush, respectively. Additional details are given in [2].
Research into brush mechanics is very limited. The applications studied include brushes for surface finishing operations [3-5], seals [6], road sweeping [1,7-12], removal of fouling from surfaces [13], post-CMP (chemical mechanical planarization) cleaning [14], and air duct cleaning [15]. The beam models that have been applied to bristle dynamics are the small and large-deflection bending theory, a discrete beam model developed by [3], and the finite element (FE) method. Large-deflection beam models have been developed by [16-18]. Further details are presented in [2].
The literature shows that brush oscillations may affect the brushing process (e.g., oscillating-rotating toothbrushes are the only type of electric toothbrush that consistently exhibits better performance than manual brushes [19]). Also, oscillations in post-CMP brushing greatly affect the coefficient of friction [14]. Thus, it is of interest to study the effect of brush oscillations on the behaviour of gutter brushes.
This paper develops a dynamic model of an oscillatory freely-rotating cutting brush, through the theory of transverse vibrations of beams and first-order bending theory. Two rotational speed functions are dealt with: sinusoidal and the VAP function, developed by the authors to obtain small angular accelerations. The variables that affect brush dynamics are identified. The model is validated through FE analyses.
The main contributions of this paper, which differ from those in [20], which provides an application of the model, are as follows: First, the development of the model is presented in detail. Second, detailed sensitivity analyses and a validation of the model through FE models derived by the authors are provided. Moreover, it is found that, for the VAP function, a condition similar to resonance tends to occur in the stronger plane for bending deflections, when the brush frequency is an odd fraction of a natural frequency of the bristle.
2. KINEMATIC ANALYSIS
The bristles of a cutting brush are of rectangular cross section and are orientated so that they deflect mainly in the brush radial direction (Fig. 1). The cutting brush rotation is characterized by variable angular speed (w) and acceleration (a). The bristle is clamped into the mounting board at point A at an angle f (the bristle mount angle) with respect to the axis of rotation (zb). The frame xG yG zG is a fixed Cartesian coordinate system, and the systems xb yb zb and xyz are fixed to the brush and the bristle, respectively.
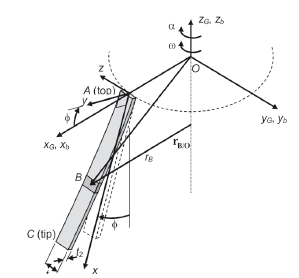
Figure 1. Deflected bristle of a cutting brush.
Bristle accelerations, gravity, and aerodynamic forces produce transverse vibration in the xy plane (the weaker plane for bending deflections), transverse vibration in xz (the stronger plane), and torsional vibration, whose interaction is difficult to model theoretically. Thus, it is assumed that the bristles do not twist and vibrate with small deflections in the weaker plane only. Also, no bristle-bristle interaction is assumed.
The kinematic analysis is based on relative-motion analysis using rotating axes. The system xb yb zb, whose fixed origin, O, coincides with the origin of the fixed system, is a rotating system characterized by w and a. Thus, the acceleration vector of any bristle element B can be expressed with reference to the rotating system by
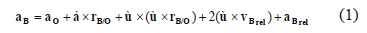
where rB/O is the position vector of B with respect to O and vBrel and aBrel are the velocity and acceleration of B relative to the rotating system, respectively. The acceleration aO is null.
The angular velocity and angular acceleration vectors of the rotating system are given by
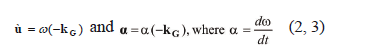
where kG is a unit vector in the zG direction, and t is time. Point B performs a rectilinear motion in the y direction (Fig. 2). Therefore,
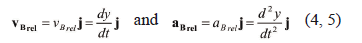
where j is a unit vector in the y direction and y is the deflection of point B. Therefore, with reference to Fig. 1, (1) can be expressed as
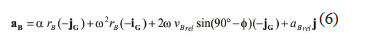
or, as jG = -k and iG = sinf i + cosf j (Fig. 1),
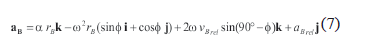
where rB is the perpendicular distance from B to the zb axis (Figs. 1 and 2) and iG, jG, i, and k are unit vectors in the xG, yG, x, and z directions, respectively. From Fig. 2, rB is given by
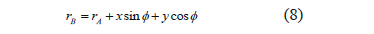
where rA is the bristle mount radius. Neglecting the last term:

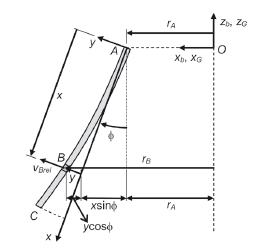
Figure 2. Bristle vibrating in the xy plane
3. DEVELOPMENT OF THE MODEL
The bristle is in dynamic equilibrium. Thus, the accelerations are dealt with by subjecting the bristle to equivalent inertia forces. However, only the acceleration in y is needed. From (5) and (7):
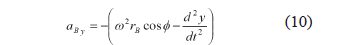
This is translated into an inertia force per unit length, q, whose direction is opposite to that of the acceleration (Fig. 3). From (9) and (10)
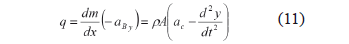
where m, r, and A are the bristle mass, density, and cross-sectional area, respectively, and

Figure 3 shows the model, where A is a built-in, fixed point in the xyz system.
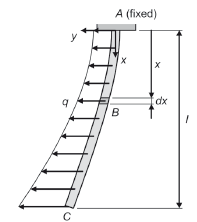
Figure 3. Modeling of the load on the bristle
Neglecting gravity, internal damping, and aerodynamic forces, from (11) and the formulation of the dynamic equilibrium equations of the element B (Fig. 4), it has that
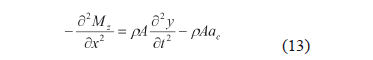
where Mz is the bending moment of the element at a distance x from the clamped end at time t.

Figure 4. Free-body diagram of a bristle element B
From first-order bending theory:

where E is the Young's modulus and Izz is the second moment of area. Thus, from (13):
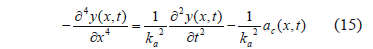
where

Equation (15) is the well-known equation of motion for the forced lateral vibration of a beam. Through the normal-mode method and the Duhamel integral, a solution of (15) is [21]
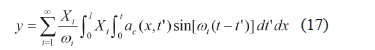
where l is the length of the bristle, wi is the angular frequency of the ith natural mode of vibration, t' is a dummy time variable, and
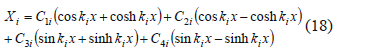
Equation (18) is the characteristic or normal mode function of a beam [22], where C1i to C4i (i = 1 to ∞) depend on the boundary conditions and
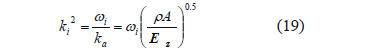
The deflection and slope at A (x = 0) and the bending moment and shearing force at C (x = l) are null. Thus, the boundary conditions are
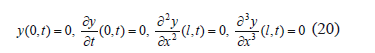
Using the method of separation of variables, the deflection for the ith mode can be given by

where yi is a time function. Thus, the boundary conditions for any ith mode can be written as
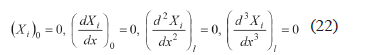
The coefficients C1i to C4i and ki (i = 1 to ∞) can be determined by (22) and the orthogonality conditions satisfied by the characteristic function. The application of the first two boundary conditions in (22) to (18) yields

A homogeneous system of two equations is obtained from the last two boundary conditions:
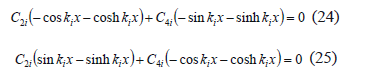
From standard linear algebra, the determinant of coefficients C2i and C4i must be equal to zero so that non-trivial solutions are obtained. Hence
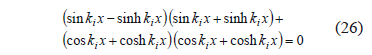
This equation produces

Combining (24) and (25) also yields a relationship between C2i and C4i:
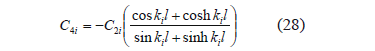
Equations (23), (27), and (28) are found in the literature [22], and C2i is obtained through the normalized orthogonality condition [21]:

It can be shown that substitution of (18) into (29), using (28), and then (27) produces

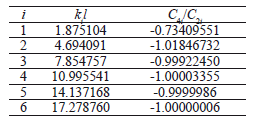
The first six roots (kil) of (27) and the ratios C4i/C2i, given by (28), are provided in Table 1.
Table 1. Values of kil and C4i/C2i for i = 1 to 6
From (19) and the known values of kil, the natural angular frequencies, wi, can be obtained:
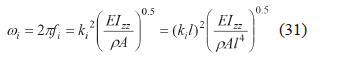
where fi is the natural frequency for the ith mode.
In order to obtain a complete solution for the equation of motion, (17) has to be dealt with further. From (12), the acceleration term ac(x,t') can be expressed as
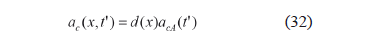
where
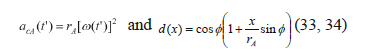
From (32), (17) can be given by
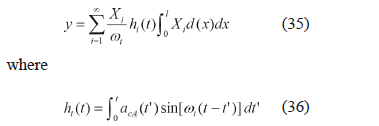
The determination of the integral in (35) yields
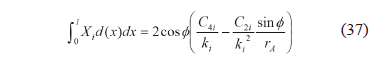
From (35), (37), (18), and (23):
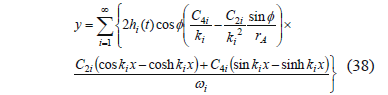
Differentiating (38) and substituting the resultant equation into (14) give
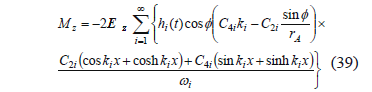
Lastly, it is necessary to evaluate the integral in (36), which depends on the acceleration acA, which in turn depends on w (33). The angular velocity functions considered are a sinusoidal function and the VAP function. Examples of curves w-t and a-t are shown in Figs. 5 and 6. The VAP function depends on smoothness parameter b, which controls the smoothness of the curves and the maximum brush accelerations.
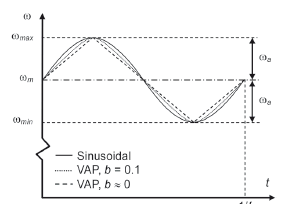
Figure 5. Angular velocity against time

Figure 6. Angular acceleration against time
For the sinusoidal function:
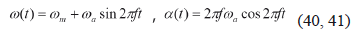
where wm and wa are the mean and alternating component of w, as shown in Fig. 5, and f is the frequency of w and a. For the VAP function:
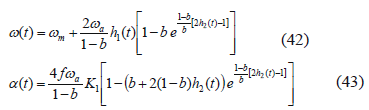
The nondimensional parameter b belongs to the interval (0, 1). When b 0, the curves are sharp and the maximum a is minimized, as shown in Figs. 5 and 6. In general, b has to be nearer to 0 than to 1 to obtain smaller accelerations than those of the sinusoidal or other w(t) functions. The functions h1(t), h2(t), and K1 are given by
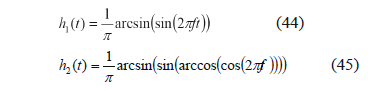
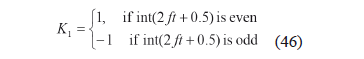
where the function "int" rounds the argument down to the nearest integer.
The integral in (36) can now be solved. From (33) and (40) and trigonometric identities, (36) for the sinusoidal function yields
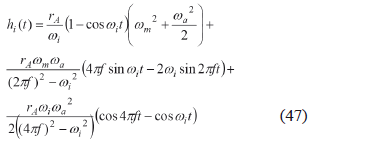
The integral for the VAP function is calculated numerically. Equation (36) is approximately:
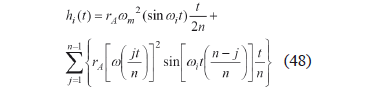
where the function w(jt/n) is obtained by substituting t by jt/n in (42), and n is an integer, large enough to obtain the desired accuracy.
4. RESULTS
4.1 Identification of brush parameters
For a given pair (x, t), y(x, t) and Mz(x, t) ((38) and (39)) depend on the type of angular speed function and on the terms wm2, f, R, b, rA, f, and l, where the angular speed ratio, R, is given by

In addition, y depends on ka (16), and Mz on EIzz and rA. From (38) and (39), both y and Mz are proportional to wm2 (for a constant R) and have a linear relationship with rA. Thus, any value of wm may be used for the study. Also, for reasons discussed in [20], this article focuses on tip deflection and bending moment at the bristle top.
4.2 Sensitivity analyses
Analyses are carried out so as to ascertain the sensitivity of the model to the number of modes considered and the value of n (48). The maximum tip deflection and top moment of a bristle oscillating up to 2 s are computed for a set of frequencies in the range 1-50 Hz, which contains the first two bristle natural frequencies.
The deflection and moment are computed using the first mode, the first two modes, etc., up to the first six. Figure 7 shows the maximum relative differences for the numbers of modes included. The differences for Mz and y are calculated as
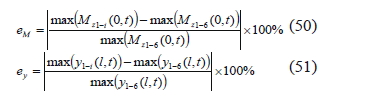
respectively, where the function "max" takes the maximum value of the argument and the subscripts 1-i and 1-6 correspond to considering the first i modes (i = 1, 2…6) and the first 6 modes, respectively. The differences for Mz are higher than those for y. E.g., the maximum differences when 4 modes are considered are 0.002 %, for y, and 0.2 %, for Mz. This may be mainly due to the fact that Mz is more sensitive than y to the bristle deformations produced by higher modes (for a given oscillation amplitude, higher modes produce deformations with smaller curvature radii). It is concluded that, for the range 1-50 Hz, the fourth and higher modes may be neglected. Thus, the model may be applied considering at least the first 3 modes.
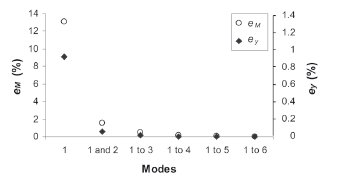
Figure 7. Relative difference in the maximum tip deflection and bending moment at the top for various numbers of modes included in the calculation
Regarding n for the VAP function (48), a set of values of n in the range 500-3000 is used. The maximum differences are given in Fig. 8, which reveals that n affects Mz more than y. This is because Mz is more influenced by higher modes and the accuracy for the higher frequencies of these higher modes is more affected by n.
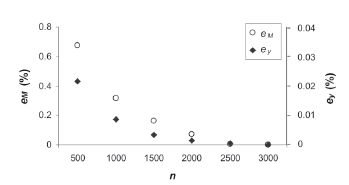
Figure 8. Relative difference in the maximum tip deflection and top moment for a set of values of n
4.3 Validity of the model
The model is validated through FE models (FEMs) implemented in ANSYS®. A small-deflection FEM is first used. The bristle is modelled with 80 3-D quadratic beam elements. Brush oscillation is modelled through an inertia load equivalent to rAac, applied during 2 s. Some analyses with various numbers of nodes and time steps were performed. The errors associated with the values selected are negligible. The first four modes are considered, and, for the VAP function, n = 2000 is used.
The following parameters are used: Material properties: E = 207 GPa, r = 7800 kg/m3 (steel); bristle dimensions: t1 = 2 mm (breadth), t2 = 0.5 mm (width), l = 240 mm (length); geometric parameters: f = 26°, rA = 112.5 mm; operating parameters: wm = 100 rpm, R = wa/wm = 0.1.
Figures 9 and 10 provide two examples in which the two models are compared. Figure 9(a) presents an example of curves y- t. As there is a close agreement between the curves of both models, Fig. 9(b) presents the differences between the deflections. Figure 10 shows an example for Mz at t = 1.702 s. This value of t was chosen because it produced the greatest difference in Mz at the fixed end (0.03 N mm).
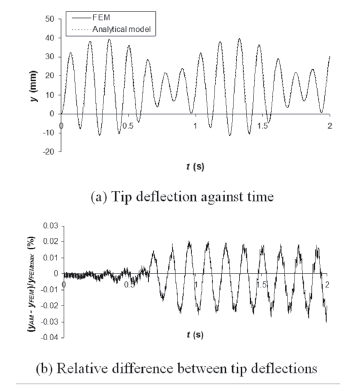
Figure 9. Comparison for tip deflection against time for the VAP function with f = 6.2 Hz and b = 0.08
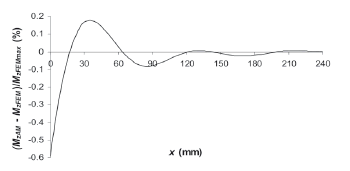
Figure 10. Comparison for Mz along the bristle at t = 1.702 s for the sinusoidal function with f = 25 Hz
For all the results, the differences between the models are less or equal to 0.6 %, for Mz, and 0.06 %, for y. The differences are computed as the ratio between the maximum difference in y or Mz and the maximum y or Mz in [0, 2 s]. However, the differences of the maximum values of y and Mz are smaller: less or equal to 0.4 % for Mz and to 0.004 % for y. These values are calculated in a manner similar to that given by (50) and (51), taking the FEM as the reference. It is concluded that the errors involved by, e.g., the integration time step, the value of n for the VAP function, and the number of nodes, are negligible, and that the analytical model is valid.
4.4 Effects of large deflections, damping, and 3-D deformations
The analytical model is validated through FEMs that include large deflection, damping, and the 3D deformations produced by all accelerations in (6). Proportional damping is assumed:
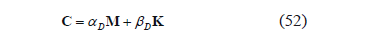
where C is the damping matrix, M is the mass matrix, K is the stiffness matrix, and aD and bD are assumed to be constant coefficients. The coefficients are obtained experimentally by analyzing the decay of the vibration amplitudes of cantilever bristles of different lengths. It was obtained that aD = 0.104 s-1 and bD = 1.07´10-5 s.
The oscillations of the brush are modelled not only by the centrifugal force, w2rB(-iG) (6), but also by the other two inertia forces, a rB(-jG) and 2w vBrel sin(90°-f)(-jG). The Coriolis component is computed at every load step by using the response of the system, and added as nodal forces. A time step of 0.5 ms is used, which produces errors smaller than about 0.1 %.
As an example, Fig. 11 compares bristle response through both the analytical model and the FEM that includes damping, large deflection, and 3D deformations. The latter will be referred to as FEMD-L-3D. From all the results, it is concluded that bristle vibrations are attenuated by internal friction and that the bristle tends to oscillate at a slightly smaller frequency than that predicted by the analytical model.
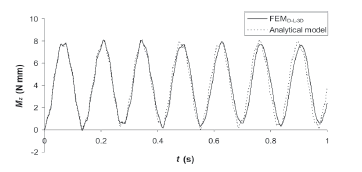
Figure 11. Bending moment against time for the VAP function with f = 17 Hz, b = 0.05, and R = 0.1
The findings show that, far from the natural frequencies of the bristle, the assumptions of small deflection and no damping are, in general, practical, provided that small intervals of time are analyzed. A detailed analysis suggests that the assumptions of small deflection and no damping tend to produce very small deviations in the maximum tip deflection and top bending moment, for the time interval [0, 1 s] and the frequency range [1, 20] Hz. The deviations due to the assumption of deflection only in the weaker plane and no twisting tend to be higher. For these cases, the ratios between the maximum z deflection (stronger plane) and y deflection (weaker plane) are estimated to be very small, but values of about 10 %, at around 20 Hz or more, may be reached. Nonetheless, the results suggest that even with z deflections of this order, the predictions of the analytical model are within 1 % error. Lastly, the maximum rotation of the bristle about its axis is less than 2°. Thus, the model is practical in most of the cases, for the frequency range and time interval analysed.
4.5 Resonant behaviour in the stronger plane
From the FEM that includes 3-D deflections, frequencies near the bristle natural frequencies in the stronger plane (xz plane in Fig. 1) (the first two natural frequencies in the stronger plane are f1s = 28.89 Hz and f2s = 181.1 Hz) produce resonance in that plane, as may be expected.
A peculiar behaviour is also revealed. A condition similar to resonance tends to occur in the stronger plane, for the VAP function with b less than about 0.4, for frequencies near odd fractions of the natural frequencies (e.g., f1s/3 = 9.63 Hz, f2s/3 = 60.36 Hz, and f1s/5 = 5.78 Hz). This phenomenon, which is due to the series of plateaus exhibited by the curve a-t (see Fig. 6, e.g., for b » 0), may be explained as follows:
As the bristle oscillates in the stronger plane, the abrupt change in angular acceleration tends to coincide with the maximum (or minimum) z bristle deflection. The directions of the deflection and angular acceleration are such that each time the latter changes direction, the bristle tends to increase its maximum deflection. This behaviour can also be explained by considering the work of the inertia force produced by the angular acceleration: this force does positive work when the force and the velocity of the bristle have the same direction. In the remaining time (shorter), the work of the force is negative. Thus, there is a net positive work that produces increased vibration amplitudes. For a detailed explanation of this, the reader is referred to a previous work [8] which deals with the vibration in the weaker plane of a flicking brush.
In the range [1, 20] Hz, the only frequency at which very large oscillations in the stronger plane seem to develop is f1s/3 = 9.63 Hz. The maximum z deflection developed in 1 s is 14.7 mm (44 % of the maximum y (weaker plane)) (Fig. 12(a)). The differences in y and Mz, between the analytical model and the FEMD-L-3D for 9.63 Hz are 6 % and 2 %, respectively. For f = f1s/5 = 5.78 Hz, bristle oscillations also tend to develop, but in the time interval studied, they are not as large as those for f1s/3. The maximum z deflection at f1s/5 is 5.0 mm (14 % of the maximum y) (Fig. 12(b)). The differences in y and Mz between the analytical model and the FEMD-L-3D for this frequency are 1 %.
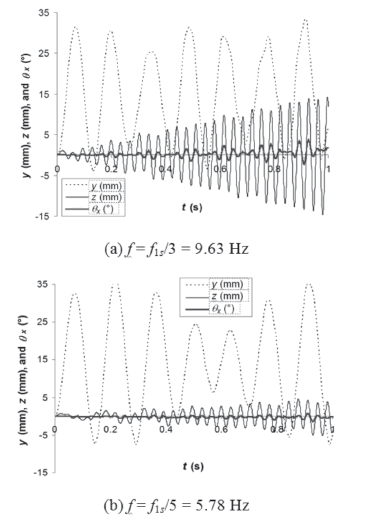
Figure 12. Tip deflections in the weaker (y) and stronger (z) plane and tip angular rotation (qx) against t, for the VAP function with b = 0.05 - FEMD-L-3D
Therefore, it has to be held in mind that the bristle will present large vibrations in the stronger plane at f1s/3 = 9.63 Hz. Consequently, in this case, the bristles tend to withstand significant Coriolis accelerations, which will affect the vibrations in the weaker plane. In addition, the superposition of oscillations in both planes tends to produce some degree of torsional vibrations. However, the torsional angles of the tip are less than 4° for this case (Fig. 12(a)).
4.6 Concluding remark
In general, the errors in the maximum tip deflection and bending moment for [1, 20] Hz and t £ 1 s are 1 % or less, except near f1 and, for the VAP function, near f1s/3. The errors near these can reach values of the order of 6 %. The results of the analytical model tend to be less accurate for higher frequencies and longer times, due to the higher effects of damping, greater vibrations in the stronger plane, and torsional vibrations that may be produced. It may not be advisable to apply the analytical model when the brush frequency is near a natural frequency for the stronger plane or an odd fraction of the first few of them. More odd fractions would cause less accuracy if very large time intervals are analyzed. Finally, larger values of n are needed for higher frequencies and longer times.
Brush oscillations have a significant effect on brush dynamics, especially for certain frequencies. The oscillations may be required when brushing compacted or sticky debris, as it has been shown that loose debris does not require high sweeping forces, provided that a suitable brush setting is used [12]. The effects of brush oscillations on a constrained brush and on effectiveness are studied through a FEM in [23].
5. CONCLUSIONS
A mathematical dynamic model of an oscillatory freely-rotating cutting brush for street sweeping was derived. The bristles were treated as cantilever beams subjected to small transverse vibrations in a plane. The normal-mode method and the Duhamel integral were used to obtain a solution of the equation of motion. A sinusoidal and the VAP angular speed, developed by the authors to obtain small brush accelerations, were studied. The parameters that affect brush behaviour were identified. It was found that bristle deflections and bending moments are proportional to the square of the mean angular speed and have a linear relationship with the mount radius. The model was validated through FEMs, which included damping, large deflection, and/or all the forces withstood by the bristles. It is concluded that the model is valid and practical for the frequency range [1, 20] Hz and t £ 1 s. Due to the plateaus in the angular acceleration versus time curve, a condition similar to resonance tends to occur in the stronger plane, for the VAP function with frequencies near odd fractions of the natural frequencies for this plane. Lastly, the model derived can be applied to the case of small transverse vibrations of a 2-D cantilever beam.
REFERENCES
[1] Peel, G., Michielen, M. and Parker, G., Some aspects of road sweeping vehicle automation, 2001 IEEE/ASME Int. Conf. Adv. Intelligent Mechatronics Proc., I-II, Como, Italy, pp.337-342, 2001. [ Links ]
[2] Vanegas Useche, L.V., Abdel Wahab, M.M. and Parker, G.A., Brush dynamics: models and characteristics, Proc. 8th ASME Con. Eng. Sys. Des. Ana. ESDA 2006, Turin, Italy, Paper No. ESDA 2006-95565, 2006. [ Links ]
[3] Stango, R.J. and Shia, C-Y., Analysis of filament deformation for a freely rotating cup brush, ASME J. Man. Sc. Eng., 119(3), pp. 298-306, 1997. [ Links ]
[4] Shia, C.Y., Stango, R.J. and Heinrich, S.M., Theoretical analysis of frictional effect on circular brush stiffness properties, Deburring and Surface Cond. 89 - Con., MR89-143-1-18, 1989. [ Links ]
[5] Stango, R.J., Heinrich, S.M. and Shia, C.Y., Analysis of constrained filament deformation and stiffness properties of brushes, ASME J. Eng. Ind., 111(3), pp. 238-243, 1989. [ Links ]
[6] Lelli, D., Chew, J.W. and Cooper, P., Combined three-dimensional fluid dynamics and mechanical modeling of brush seals, ASME J. Turbomachinery, 128(1), pp. 188-195, 2006. [ Links ]
[7] Vanegas Useche, L.V., Abdel Wahab, M.M. and Parker, G.A., Theoretical model for the dynamics of an unconstrained cutting brush of a street sweeper, Proc. 8th ASME Conf. Eng. Sys. Des. Analysis ESDA 2006, Turin, Italy, Paper No. ESDA2006-95563, 2006. [ Links ]
[8] Vanegas Useche, L.V., Abdel Wahab, M.M. and Parker, G.A., Dynamics of an unconstrained oscillatory flicking brush for road sweeping, J. Sound Vibration, 307, pp.778-801, 2007. [ Links ]
[9] Peel, G.M. and Parker, G.A., Initial investigations into the dynamics of cutting brushes for sweeping, ASME J. Dynamic Syst. Meas. Con., 124(4), pp. 675-681, 2002. [ Links ]
[10] Abdel Wahab, M., Wang, C., Vanegas Useche, L.V., and Parker, G.A., Finite element models for brush-debris interaction in road sweeping, Acta Mechanica, 215(1-4), pp. 71-84, 2010. [ Links ]
[11] Vanegas Useche, L.V., Abdel Wahab, M.M. and Parker, G.A., Determination of friction coefficients, brush contact arcs and brush penetrations for gutter brush-road interaction through FEM, Acta Mechanica, DOI 10.1007/s00707-011-0490-2. [ Links ]
[12] Vanegas Useche, L.V., Abdel Wahab, M.M., and Parker, G.A., Effectiveness of gutter brushes in removing street sweeping waste, Waste Management, 30(2), pp. 174-184, 2010. [ Links ]
[13] Holm, E.R., Haslbeck, E.G. and Horinek, A.A., Evaluation of brushes for removal of fouling from fouling-release surfaces, using a hydraulic cleaning device, Biofouling, 19(5), pp. 297-305, 2003. [ Links ]
[14] Philipossian, A. and Mustapha, L., Effect of tool kinematics, brush pressure and cleaning fluid pH on coefficient of friction and tribology of post-CMP PVA brush scrubbing processes, Mat. Res. Soc. Sym. Proc., 767, pp. 209-215, 2003. [ Links ]
[15] Holopainen, R. and Salonen, E.M., Modelling the cleaning performance of rotating brush in duct cleaning, Energy & Buildings, 34, pp. 845-852, 2002. [ Links ]
[16] Aristizabal-Ochoa, J.D., Estabilidad y análisis de segundo orden de estructuras de vigas y columnas de Timoshenko con conexiones semirrígidas: método pendiente deflexión, Dyna, 159, pp. 7-21, 2009. [ Links ]
[17] Aristizabal-Ochoa, J.D., Análisis de primer y segundo-orden y estabilidad de pórticos con conexiones semirrígidas: método de Hardy Cross (I-teoría), Dyna, 167, pp. 103-111, 2011. [ Links ]
[18] Rodríguez-Gutiérrez, J.A. and Aristizabal-Ochoa, J.D., General analytical approach for prestressed and non-prestressed concrete beam-columns reinforced with bonded and unbonded composites: (I) theory, Dyna, 168, pp. 19-27, 2011. [ Links ]
[19] Deery, C. et al., The effectiveness of manual versus powered toothbrushes for dental health: a systematic review, J. Dentistry, 32, pp. 197-211, 2004. [ Links ]
[20] Vanegas Useche, L.V., Abdel Wahab, M.M. and Parker, G.A., Dynamics of a freely-rotating cutting brush subjected to variable speed, Int. J. Mech. Sc., 50(4), pp.804-816, 2008. [ Links ]
[21] Weaver, W. Jr., Timoshenko, S.P. and Young, D.H., Vibrations Problems in Engineering, fifth ed., John Wiley & Sons, Inc., NY, 1990. [ Links ]
[22] Rao, S.S., Mechanical Vibrations, fourth ed., Pearson Education, Inc. New Jersey, 2004. [ Links ]
[23] Vanegas Useche, L.V., Abdel Wahab, M.M. and Parker, G.A., Dynamic finite element model of oscillatory brushes, Fin. Ele. Anal. Des., doi:10.1016/j.finel.2011.02.008. [ Links ]














