Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.170 Medellín dez. 2011
EFFECT OF SEDIMENTARY AND METAMORPHIC AGGREGATE ON STATIC MODULUS OF ELASTICITY OF HIGH-STRENGTH CONCRETE
EFECTO DE LOS AGREGADOS SEDIMENTARIOS Y METAMORFICOS EN EL MÓDULO DE ELASTICIDAD ESTATICO DEL CONCRETO DE ALTA RESISTENCIA
JUAN LIZARAZO-MARRIAGA
Ph.D. Grupo de Investigación en Estructuras y Materiales GIES (A) Universidad Nacional de Colombia, Bogotá, Colombia, jmlizarazom@unal.edu.co
LUCIO GUILLERMO LÓPEZ YÉPEZ,
Ms.C. Grupo de Investigación en Estructuras y Materiales GIES (A), Universidad Nacional de Colombia, Bogotá, Colombia, lglopezy@unal.edu.co
Received for review February 17th, 2011, accepted August 10th, 2011, final version August 29th, 2011
ABSTRACT: Taking into account the increasing use of high-strength concrete as a structural material in Colombia, this paper shows the results of research carried out to investigate the effect of different types of coarse aggregate on the static elastic modulus, the compressive strength, the concrete density, and the pulse velocity. To do this, concrete mixes were cast using three different water binder ratios (w/c) (0.36, 0.32, and 0.28). Ordinary Portland cement and pulverized silica fume (SF) were used as cementitiuos materials, while four types of coarse aggregates obtained from different sources near Bogota, Colombia were utilized to prepare the concrete samples. Results were analyzed statistically and these showed that the behavior of all the tests followed a normal frequency distribution. Correlations were found among the mixes. From the experimental data obtained in this study, it was concluded that the equations proposed in standard codes overestimated the modulus of elasticity of high-strength concrete, so empirical equations were obtained in order to predict the elastic modulus of elasticity in high-strength concrete.
KEYWORD: modulus of elasticity, high-strength concrete, aggregate
RESUMEN: Considerando la creciente utilización de hormigón de alta resistencia como material estructural, este artículo presenta los resultados de un trabajo experimental llevado a cabo con el fin de investigar el efecto de diferentes tipos de agregados gruesos sobre el módulo estático elástico, la resistencia a la compresión, la densidad del hormigón y la velocidad del pulso. Para lograr esto, se usaron diferentes relaciones agua cementante (a/c) (0.36, 0.32, y 0.28) y cuatro tipos de agregados diferentes, todos del área de influencia de Bogotá, Colombia. Como materiales cementantes se usaron cemento Portland y microsílice (SF). Los resultados experimentales fueron analizados estadísticamente, de donde se encontró que todos los ensayos se comportan siguiendo una distribución de frecuencia normal. De los datos experimentales obtenidos se concluyó que las ecuaciones propuestas en los códigos sobreestiman el módulo de elasticidad del hormigón de alta resistencia, por lo que se proponen ecuaciones empíricas como alternativa.
PALABRAS CLAVE: módulo de elasticidad, concreto de alta resistencia, agregados
1. INTRODUCTION
Almost all concrete structural analysis and design is carried out using mechanical properties such as the modulus of elasticity. This is used to calculate deflections, are-stress losses of concrete members and design drifts [1]. The modulus of elasticity is given by the slope of the stress and strain curve. This relationship behaves linearly in experiments up to 0.40 of the maximum compressive strength (f´c); after that point, it behaves non-linearly [2]. There are different types of elastic moduli: (a) the tangent modulus given by the tangent of the stress-strain curve at any point, where the initial modulus corresponds approximately to the dynamic modulus of elasticity; (b) the secant modulus given by the line from the origin to any point on the curve; and (c) the chord modulus given by the line from a small strain (usually 50 mm/m) to a point on the curve corresponding to a 0.40 f´c, this is known as the static modulus of elasticity [3].
Aggregate plays an important role in concrete properties such as strength, stiffness, dimensional stability, durability, workability, and economy. Therefore, the physical and chemical properties of aggregates are of interest for concrete technologists because they determine the quality and features of concrete. According to ACI-318 [4], concrete is sensitive to the geological origin of natural aggregates. Hence, aggregate's porosity is an important characteristic that affects the elastic modulus of concrete because dense aggregates have better mechanical properties [5]. Aïtcin [6], according to experimental results stated that aggregates are as important as the water/binder ratio in terms of the modulus of elasticity, especially in high-strength concrete. The term high-strength concrete is used in this paper for concrete with a compressive strength in excess of 41 MPa, and water-cement ratios (w/c) in the range of 0.25 to 0.40.
The modulus of elasticity used in concrete design computations are usually estimated from empirical expressions that assume direct dependence of the elastic modulus on the strength, concrete unit weight, and the aggregate origin [2]. For high-strength concrete, deviations from empirical expressions are highly dependent on the properties and proportions of the coarse aggregate [4]. Taking the increasing use of high-strength concrete as a structural material into account, this paper reports on the results of research undertaken for investigating the effect of four different types of coarse aggregate on the static elastic modulus, compressive strength, oncrete density, and pulse velocity. To achieve this, concrete mixes were cast using three different w/c (0.36, 0.32, and 0.28) for a total of 12 mixtures.
2. EXPERIMENTAL PROGRAMME
2.1 Materials
An ordinary Portland cement type I (OPC) with no mineral admixtures and a commercial pulverized silica fume (SF) were used as cementitiuos materials. Table 1 shows the chemical composition of silica fume and Fig. 1 shows the particle size analysis for the raw materials used.
Table 1. Chemical composition of Silica fume
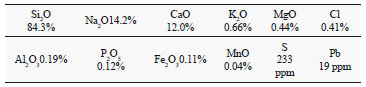
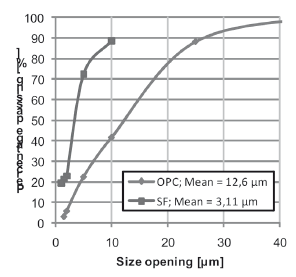
Figure 1. Particle size analysis of cementitious materials
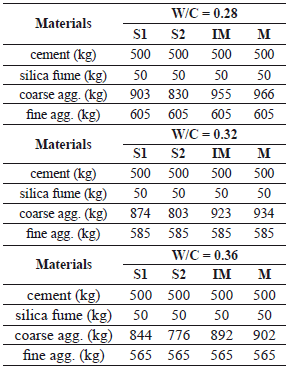
Four types of coarse aggregate, obtained from different sources near the area of influence of Bogota, Colombia were utilized to prepare the concrete mixtures. The materials were selected from the most common local quarries and were classified according to their geological origin. Aggregates which were named (S1) and (S2) were obtained from sedimentary rocks; the first was extracted from the banks of the Tunjuelo River in the south of Bogota, and the later was extracted from the Tabio quarries in the north of the city. Aggregate (MI) had a mixed geological origin; it was formed by igneous rocks with small veins of metamorphic origin. It was from the banks of the Coello River in Chicoral, Tolima. The fourth aggregate (M) was from metamorphic rocks, obtained from the banks of the Guayuriva River near Villavicencio, Meta. The physical properties of the coarse aggregates selected for this research are shown in Table 2.
Table 2. Coarse aggregate properties
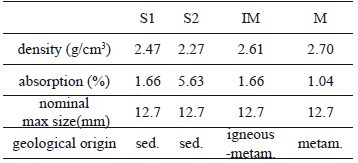
Natural sand was used for all mixtures. It was obtained from the (S2) source. The physical properties of the fine aggregates selected are summarized in Table 3. Figure 2 shows the size distribution for coarse and fine aggregates.
Table 3. Fine aggregate properties

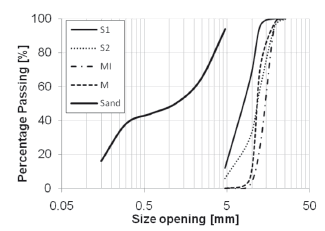
Figure 2. Aggregate size distribution
Sixteen batches of concrete were produced and 10 cylinder specimens of a 150 mm diameter and a 300 mm height were cast for each one. Water to cementitious (W/C) ratios of 0.28, 0.32, and 0.36 were used, so it was necessary to apply a high-range water-reducing commercial chemical admixture (based on policarboxilates) in order improve the workability of the concrete mixtures. For all mixes, the cementitious content (OPC + SF) was 550 kg/m3, which corresponds to the high cement content normally used in the category of high-strength concrete. The amount of silica fume content was 10 % of the total OPC content (kg/m3). Table 4 shows a summary of the concrete mix design used. After mixing, all test specimens were demoulded at 1 day, and then cured in water at a temperature of 22 ± 2 ºC.
2.2 Experimental methods
In order to investigate the effect of aggregates on the related mechanical properties, the concrete mixtures cast were tested after 28 days of water curing. Compressive strength tests were carried out according to ASTM C39 using a universal test machine with a capacity of 200 tons. It was reported by Aïtcin [6] that the measurement of the elastic modulus of high-performance concrete can be done in the same way as it is done for normal concrete; therefore, the modulus of elasticity according to ASTM C469 was obtained before failure in a compression strength test. The ultrasonic pulse was measured using the standard ASTM C597, which covers the determination of the pulse propagation of compressional waves in concrete. This non-destructive technique was measured using a Pundit ultrasonic concrete tester with 54 kHz longitudinal wave transducers located at each end of the samples. The principle of this testing technique is that the velocity of an ultrasonic pulse through a solid medium is related to its density and elastic properties. The concrete unit weight was calculated as the relationship between the mass of the specimen and the bulk or apparent volume (defined as an ideal cylinder).
3. RESULTS AND DISCUSSION
3.1 Basic statistics
For each mixture, statistics were performed for each property investigated. 10 similar specimens for each point were used in order to guarantee statistical validity. The parameters calculated were the mean, standard deviation, coefficient of variation, range, and p-value. The first four parameters do not need additional explanation because they are of general application in engineering. In contrast, the p-value refers to a probability index used in hypothesis tests where a null hypothesis is either accepted or rejected.
Anderson-Darling tests for normality were carried out for all experimental properties in order to know whether the data can be modeled statistically following a normal distribution. A distribution model provides a theoretical distribution that can be used to predict the possibility of occurrence of certain values [8]. The p-value calculated represented the probability of rejecting the following proposed hypothesis: "The data obtained from experimental observations of compressive strength, static modulus of elasticity, ultrasonic pulse velocity, and concrete unit weight behaved according to a normal distribution." The smaller the p-value, the smaller the probability that there will be an error in the hypothesis. A recommended value often used is 0.05; that is, the hypothesis should be rejected when the p-value is less than 0.05 [9]. Results of the statistical analysis are shown in Tables 5 and 6.
Table 5. Basic statistics of the compressive strength and the modulus of elasticity
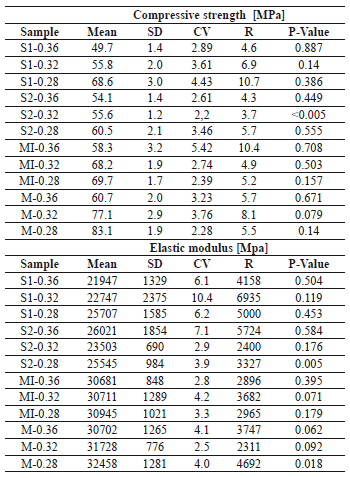
Table 6. Basic statistics of the pulse velocity and the concrete unit weight
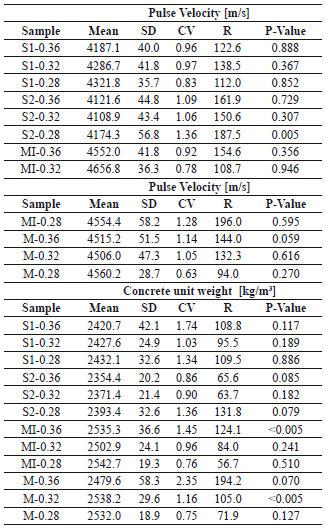
Statistical results showed that for all the experiments carried out, the data measured behaved according to a normal distribution. Although in specific mixtures, values of p-value were less than 0.05, it is assumed that, from a general point of view, the model follows the hypothesis initially proposed: "The experimental data follows a normal distribution." In normal concrete compressive strength tests, ACI 214 stated that experimental data can be treated as if they fall into a distribution similar to the normal frequency distribution curve [10]; however, for high-strength concrete, it was reported by ACI that frequency distributions follow skewed distributions. That is, the data are not symmetrical around the mean. Cook [11] stated that normal distribution is appropriate in most cases when the strength of the concrete does not exceed 70 MPa. In this research, it was assumed that all the material properties investigated (compressive strength, elastic modulus, pulse velocity, and concrete unit weight) followed a normal distribution according to the analysis conducted.
Results of compressive strength are shown in Fig. 3 for all mixtures simultaneously, and as probability density functions. The vertical scale on the graph resembles the calculated theoretical frequency. The horizontal axis is a linear scale in terms of MPa. The line forms an estimate of the cumulative distribution function for the population from which data are drawn and describes the relative likelihood for this random variable to occur at a given point [9]. The curve obtained for each mixture permitted an examination of the shape and spread of sample data.
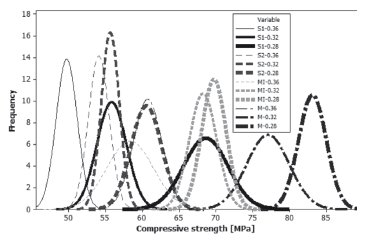
Figure 3. Compressive strength probability density functions
It can be deduced from the mean of the data for each mixture (Fig. 3) that the water to binder ratio and the type of aggregate have a significant effect on the compressive strength of concrete. As was expected, the compressive strength increased with a reduction of the water to binder ratio. In the same way, aggregates from sedimentary rocks showed the lowest compressive strength, while the highest compressive strength was measured in the specimens prepared with the metamorphic ones.
The theoretical probability density function obtained from experimental data for static modulus of elasticity is shown in Fig. 4. For this property, the type of aggregate is the most relevant parameter. Two groups of results can be seen in this Fig., i.e., samples made with sedimentary rocks are concentrated on the left with a lower modulus value, while metamorphic samples showed a higher value of elasticity modulus. Samples with similar aggregate behave similarly. The density functions showed that for concrete with the same water to binder ratio there is just a small probability that sedimentary samples have higher elastic modulus than the metamorphic samples. Although the water to binder ratio also has an important influence on the static modulus of elasticity, from Fig. 4 it can be seen that for similar aggregates, the density functions tend to overlap.
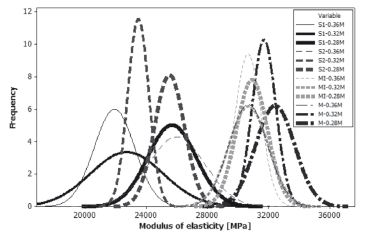
Figure 4. Static modulus of elasticity probability density functions
In the same way as the static modulus of elasticity, the probability density functions for the pulse velocity and concrete unit weight are shown in Figs. 5 and 6, respectively. The behavior of these parameters is similar to that found previously in the modulus of elasticity density functions; depending on the aggregate origin, the physical parameters have a different behavior. Regardless of the water to binder ratio, samples with similar aggregates tend to be concentrated around them. As was expected, the concrete using metamorphic aggregates showed better performance than their counterparts in terms of pulse velocity and concrete unit weight. This was explained by the fact that pulse velocity is strongly linked to the density and elastic properties, and for metamorphic rocks, density and mechanical properties can be expected to be of a better quality under normal conditions [5].
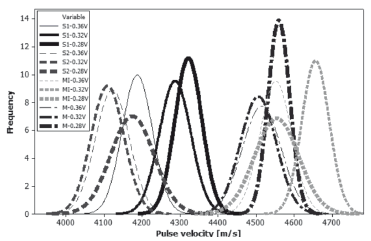
Figure 5. Pulse velocity probability density functions
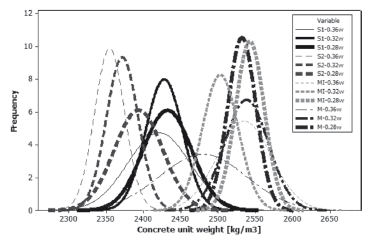
Figure 6. Concrete unit weight probability density functions
3.2 Correlation among measured variables
The relationship between the properties measured experimentally (compressive strength, elastic modulus, pulse velocity, and concrete unit weight) are displayed in Fig. 7 in a group of scatter plots as a collection of points that show the relationships among all of them. In the same way, Table 7 shows the correlation matrix obtained, where the coefficient of determination R2 was found using a least squares regression analysis for the best type of equation that fit the data.
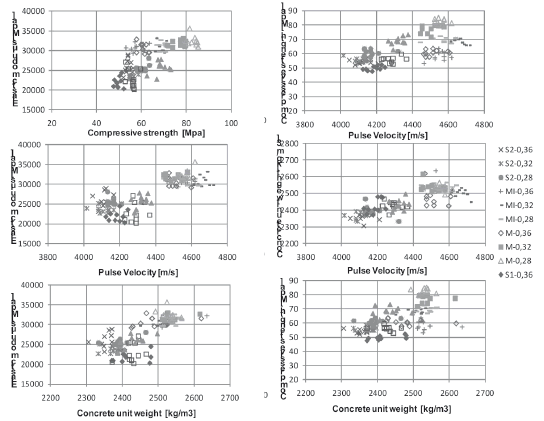
Figure 7. Relationships between physical parameters measured
Table 7. Correlations among the parameters measured
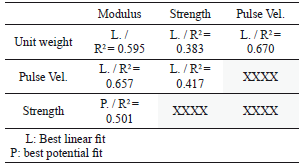
Not very strong correlations were found for the relationships investigated (values higher than R2 = 0.8); however, the coefficients of determination showed that statistically there is a tendency for the proposed relations. The correlation between the static modulus of elasticity and the unit weight, pulse velocity, and compressive strength are in the range of 0.5-0.65, the pulse velocity being a better predictor. Linear functions for unit weight and pulse velocity were obtained, while for compressive strength, a potential relationship was obtained in the same way as ACI 318. Using the unit weight and the pulse velocity as predictors of the compressive strength, the coefficients of determination were in the range of 0.38-0.41, showing the small dependence of these parameters on the strength. Among all the relationships studied, the best correlation obtained was between the ultrasonic pulse and the concrete unit weight (R2 = 0.67).
3.3 Assessment of the standard equations
Concrete properties such as modulus of elasticity, tensile strength, shear strength, and bond strength are frequently expressed in terms of compressive strength. Generally, expressions for these quantities have been empirically established based on data for concrete. Standards like ACI 318, ACI 363 and NSR10 [11] have for a long time used the square root of the compressive strength in order to predict the static modulus of elasticity. The coefficients and equations used by these standards are the result of extensive experimental research and are updated frequently. Figure 8 shows the different equations proposed, establishing a direct relationship between the root of the compressive strength and the modulus of elasticity.
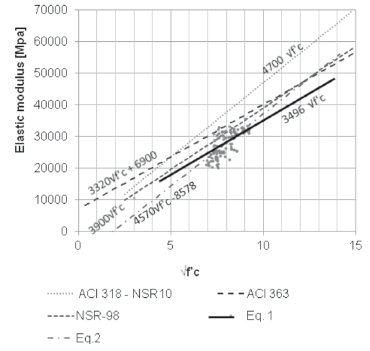
Figure 8. Static modulus of elasticity expressions
For normal weight concrete, ACI318-08 and NSR10 allow for the use of the expression 4700(f´c)0.5. From the experimentally measured modulus (scatter points Fig. 8), it can be seen that this expression overestimates significantly the modulus of elasticity for samples using aggregate from the influence area of Bogota, Colombia. However, the ACI318 and NSR-10 specify a compressive strength range of up to 40 MPa as a limit for which the expressions are valid. Similarly, ACI363 provides the expression 3320(f´c)0.5 + 6900 [MPa] for normal weight concretes in the range of resistances of 21 MPa < f´c < 83 MPa. Like the ACI318 expression, this equation tends to overestimate the elastic modules; however it does so to a lesser extent.
Using least squares regression analysis on the experimental data, the linear correlation between the square root of the compressive strength and the static modulus of elasticity was obtained. Two relationships are proposed in this research, which are fitted using the same set of data. The difference between them is that in the proposed Eq. 1, the linear fit is forced to cross the origin, unlike in Eq. 2 where there is an intercept with the vertical-axis. It is considered that the previous equations are valid for high-strength concrete compressive strengths over 50 MPa and under 85 MPa. It is important to notice that although the equation given by NSR98 was the most consistent with the measured data, this tends to overestimate the elastic modulus more than the standards mentioned above.
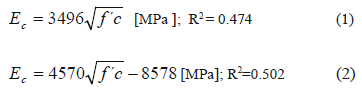
In addition to the equations presented above, according to ACI318, the modulus of elasticity for concrete can be taken as a function of the density (unit weight) of normal weight concrete. This ACI equation (wc1.5)0.043(f´c)0.5 in [MPa] is valid for concrete with a unit weight between 1440 and 2560 kg/m3. Figure 9 shows the former ACI equation, the experimental data, and the best fit using a least squares regression model. Equation 3 corresponds to that best fit of the experimental data. It can be seen that the inclusion of the unit weight improves the correlation, showing once again the influence of the aggregate on the elastic modulus. Although the experimental data was modeled successfully with an equation similar to the one proposed by ACI, numerically it is observed that it is overestimated by a ratio of two. The proposed equation for local aggregate having a compressive strength between 50 MPa and 85 MPa is given by Eq. 3.
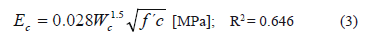
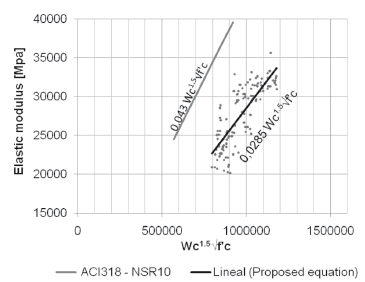
Figure 9. Static modulus of elasticity expressions
4. CONCLUSIONS
For high-strength concrete, the origin of aggregate (metamorphic, igneous, or sedimentary) significantly influences the static modulus of elasticity, the concrete unit weight, the pulse velocity, and (slightly less) the compressive strength.
Equations proposed in standard codes such as ACI318, NSR-10, and ACI363 overestimate the modulus of elasticity of high-strength concrete made using coarse aggregate obtained from the area of influence of Bogota, Colombia. Concrete design equations included in national Colombian codes should be obtained from national research programs and not adapted from international standards.
From the experimental data, equations were obtained to predict the elastic modulus of elasticity in high-strength concrete. It is believed that these equations are a better approximation than those currently contained in existing codes.
Other research should be performed with aggregates used in large capital cities in order to find a nationwide formulation.
5. REFERENCES
[1] Carrillo, J., González, G. and Jiménez, M. Incidencia del diámetro de extracción de núcleos de concreto en el análisis de derivas de estructuras aporticadas, Dyna, 152,74, 2007. [ Links ]
[2] Mehta, P. K. and Monteiro, P. J. M. Concrete, Microstructure, properties and materials, McGraw Hill, New York, 2006. [ Links ]
[3] ASTM-C597. Standard test method pulse velocity through concrete. American society for testing and materials, 1997. [ Links ]
[4] ACI318-08, Building code requirements for structural concrete and commentary. American Concrete Institute, 2008. [ Links ]
[5] Langer, W. H. and Knepper, D. H. Geologic characterization of natural aggregate: a field geologist guide to natural aggregate resorce assesment, open file repor 95-582, 1995. [ Links ]
[6] Aitcin, P. C. High performance concrete, E & FN SPON, London-New York, 2004. [ Links ]
[7] ACI-363, State of the art report on high-strength concrete. Manual Concrete Practice 2006. American Concrete Institute, 1992. [ Links ]
[8] Ruffolo, R. M. and Shakoor, A. Variability of unconfined compressive strength in relation to number of test samples. Enginnerind geology, 108, 16-23. 2009. [ Links ]
[9] Minitab 15. Meet Minitab 15 para windows. 2007 [ Links ]
[10] ACI-214, Evaluation of strength test results of concrete. Manual concrete practice 2006. American Concrete Institute, 2002. [ Links ]
[11] CooK, J. E. Research and application of high-strength concrete using class C fly ash. Concrete International, 4, 1982. [ Links ]
[12] AIS 2010. Reglamento Colombiano de Contrucción Sismo Resistente NSR-10. Bogota D. C.: Asociación Colombiana de Ingeniería Sísmica, 2010. [ Links ]