Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.79 n.171 Medellín jan./fev. 2012
KAOLIN QUALITY DETERMINATION THROUGH AN ALGORITHM BASED ON NON-PARAMETRIC FUZZY LOGIC
DETERMINACIÓN DE CALIDAD DE CAOLÍN MEDIANTE UN ALGORITMO BASADO EN LÓGICA DIFUSA NO PARAMÉTRICA
CELESTINO ORDÓÑEZ
Doctor en Ingeniería de minas, Universidad de Vigo, Campus Lagoas-Marcosende, Vigo, Spain, cgalan@uvigo.es
ÁNGELES SAAVEDRA
Doctora en Matemáticas, Universidad de Vigo, Campus Lagoas-Marcosende, Vigo, Spain, saavedra@uvigo.es
MARÍA ARAÚJO
Doctor en Ingeniería de minas, Universidad de Vigo, Campus Lagoas-Marcosende, Vigo, Spain, maraujo@uvigo.es
EDUARDO GIRÁLDEZ
Doctor en Ingeniería de minas, Universidad de Vigo, Campus Lagoas-Marcosende, Vigo, Spain, edugiraldez@gmail.com
Received for review June 11th, 2010, accepted March 10th, 2011, final version March, 14th, 2011
ABSTRACT: In this article we describe a new fuzzy supervised classification method that is a modification of the fuzzy pattern-matching multidensity classifier. The latter has been demonstrated to be one of the most effective classifiers for non-convex classes. Implementing a non-parametric density estimator in one stage of the parametric method, we developed a fuzzy non-parametric classifier that manages to avoid some of the problems associated with the parametric method. The method was applied to a mineralogy problem consistingof classifying kaolin samples according to different ceramic quality levels. Our results produced error percentages that were lower than those for the parametric method.
KEYWORDS: classification, fuzzy set, non-parametric fuzzy logic, kaolin quality
RESUMEN: En este artículo se describe un método de clasificación supervisado que es una modificación del clasificador multidensidad de ajuste de patrones difuso. Se ha demostrado que este último es uno de los clasificadores más efectivos para clases no convexas. Implementando un estimador de densidad no paramétrico en una etapa del método paramétrico hemos desarrollado un clasificador no paramétrico difuso que evita algunos de los problemas asociados al método paramétrico. El método se ha aplicado a un problema de mineralurgía consistente en clasificar muestras de caolín de acuerdo con diferentes niveles de calidad cerámica. Nuestros resultados producen porcentajes de error que son inferiores a los obtenidos mediante el método paramétrico.
PALABRAS CLAVE: clasificación, conjunto difuso, lógica difusa no paramétrica, calidad de caolín
1. INTRODUCTION
In general terms, the discrimination or classification problem can be described in terms of a set of statistical techniques that enable us to study differences between populations or classes, established a priori and not necessarily exclusive. These techniques classify and assign elements to classes for which specific characteristics are known. Classification is said to be supervised when learning is implemented using a set of pre-classified elements. The aim is to predict the class to which a new element not included in the initial training set belongs. A popular procedure aimed at achieving this goal consists of adjusting the classification functions by using a training set and then testing the percentage of correct classifications using a test set. Both the training and test sets are composed of pre-classified elements from an initial sample.
The fact that many classification methods have been developed in recent years complicates the selection of a method suitable for a given classification problem (see [1,2] for a description of traditional methods and how these are implemented). A supervised classification method that uses the fuzzy set theory during training and/or a subsequent operation is called a fuzzy classification method [3]. These classification methods typically apply fuzzy set theory as described by Zadeh [4] (see [5,6] for an introduction and description of different fuzzy classification methods). It is important to point out that some of the fuzzy methods mentioned in the references given above refer to non-fuzzy methods as particular cases.
In this article we describe a non-parametric variant of the fuzzy pattern-matching multidensity classifier developed by Devillez [7] that we used to classify kaolin samples into 3 ceramic quality grades on the basis of 10 variables reflecting chemical composition. Our aim was to determine kaolin quality on the basis of values for explanatory variables obtained from a chemical analysis.
2. METHODS
2.1.1 Fuzzy supervised classfication
Take a sample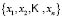 composed of
composed of 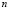 elements, for which a random
elements, for which a random 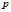 -dimensional variable
-dimensional variable 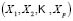 is observed. Each sample element
is observed. Each sample element 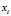 is a vector of the form:
is a vector of the form:
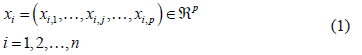
Let us assume, furthermore, that each of the elements is classified into one of the 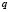 predetermined classes
predetermined classes 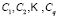 making up the classification space. Allocation of a new element
making up the classification space. Allocation of a new element 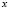 from the classification space to one of the
from the classification space to one of the 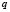 classes
classes 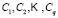 is the main goal of a classification problem that has been handled differently in recent years. A typical procedure in many of the statistical methods used to resolve this kind of problem is to determine
is the main goal of a classification problem that has been handled differently in recent years. A typical procedure in many of the statistical methods used to resolve this kind of problem is to determine 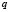 membership functions
membership functions 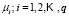 that quantify degree of membership to different classes. A new element from the classification space,
that quantify degree of membership to different classes. A new element from the classification space,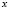 , is allocated to the class
, is allocated to the class 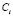 for which it obtains the greatest score; in other words:
for which it obtains the greatest score; in other words: 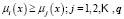 .
.
Supervised fuzzy classification methods have as their goal the calculation of the membership functions for each class. The sample is divided into two sub-samples, one for training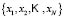 and another for testing
and another for testing 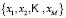 with the training set used in the learning phase. The learning phase consists of selecting a set of membership functions
with the training set used in the learning phase. The learning phase consists of selecting a set of membership functions 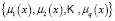 that are optimal from the point of view of classification. Finally, the test sample is used to validate the accuracy of the procedure.
that are optimal from the point of view of classification. Finally, the test sample is used to validate the accuracy of the procedure.
The classical fuzzy pattern-matching algorithm first described by Dubois et al. [8] was adapted by Devillez [7] as a fuzzy pattern matching multidensity classifier. This classifier, which has been demonstrated to be one of the most effective classifiers for classes with non-convex shapes, is implemented as described below.
2.1.1 Training
Each of the classes 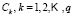 that make up the classification space are divided into a number
that make up the classification space are divided into a number 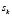 of sub-classes using the fuzzy
of sub-classes using the fuzzy 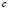 -means algorithm [9,10] which minimizes the within-class sum of squared errors in the following conditions:
-means algorithm [9,10] which minimizes the within-class sum of squared errors in the following conditions:
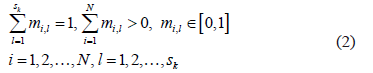
where 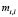 are the membership functions to be determined. The objective function to be minimized is given by the following expression:
are the membership functions to be determined. The objective function to be minimized is given by the following expression:
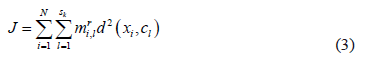
where 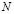 is the number of data items in the training subset,
is the number of data items in the training subset,  is the vector representing the centroid of the
is the vector representing the centroid of the  th sub-class,
th sub-class, 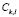 of the class
of the class 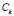 ,
,  is the fuzzy exponent, which should, strictly speaking, be greater than 1, and where
is the fuzzy exponent, which should, strictly speaking, be greater than 1, and where 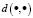 is a measure of the distance between two points calculated as:
is a measure of the distance between two points calculated as:
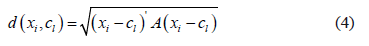
where 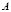 is the distance norm matrix, identity matrix for the Euclidean distance or the inverse of the variance-covariance matrix for the Mahalanobis distance.
is the distance norm matrix, identity matrix for the Euclidean distance or the inverse of the variance-covariance matrix for the Mahalanobis distance.
Minimizing the objective function 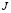 offers the membership functions for each sub-class as a solution:
offers the membership functions for each sub-class as a solution:
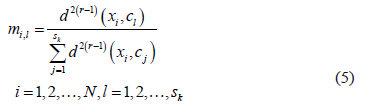
This procedure can be implemented, for example, using the FuzME program [11].
Following the application of the algorithm, a set 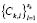 of sub-classes is obtained for each class
of sub-classes is obtained for each class 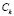 . The elements in the training set
. The elements in the training set 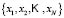 are allocated to the sub-class with the maximum membership function as calculated by the fuzzy algorithm.
are allocated to the sub-class with the maximum membership function as calculated by the fuzzy algorithm.
Learning continues with the calculation of a membership function for each sub-class and each variable 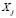 . These functions can be calculated on the basis of the probability estimated from the histograms for the data. In other words, given a sub-class
. These functions can be calculated on the basis of the probability estimated from the histograms for the data. In other words, given a sub-class 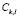 and a variable
and a variable 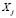 , the histogram is calculated using the values
, the histogram is calculated using the values 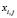 of the elements
of the elements 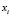 from the training set that have been allocated to the sub-class
from the training set that have been allocated to the sub-class 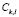 .
.
Determined during the training process are 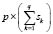 histograms that have to be transformed into fuzzy membership functions. The membership functions can be deduced from the probability distributions associated with the calculation of the histograms using any of the transformations proposed by Dubois et al. [12]. Following Devillez [7], we implemented one of the first probability-possibility transformations, introduced by Dubois and Prade [13], who define the probability distribution associated with a histogram as the discrete distribution given by
histograms that have to be transformed into fuzzy membership functions. The membership functions can be deduced from the probability distributions associated with the calculation of the histograms using any of the transformations proposed by Dubois et al. [12]. Following Devillez [7], we implemented one of the first probability-possibility transformations, introduced by Dubois and Prade [13], who define the probability distribution associated with a histogram as the discrete distribution given by 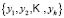 -which are central values in the histogram bins-and by the probabilities
-which are central values in the histogram bins-and by the probabilities 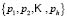 -calculated as the ratio between bin height and the sum of all the heights. The probability values are next arranged in descending order:
-calculated as the ratio between bin height and the sum of all the heights. The probability values are next arranged in descending order: 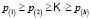 . The values for the membership function associated with the values
. The values for the membership function associated with the values 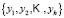 are then calculated:
are then calculated:
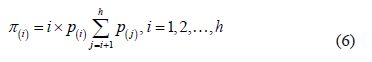
The membership function is completed by means of a linear interpolation of the above values.
The learning phase concludes with 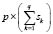 membership functions, which we can denote as:
membership functions, which we can denote as:
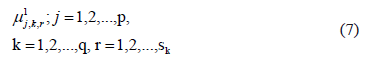
2.1.2 The nonlinear classification rule
For an element 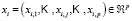 from the test sample
from the test sample 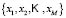 the degree of membership to each sub-class
the degree of membership to each sub-class 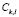 is evaluated by applying the minimum operator to the membership functions calculated in the training phase:
is evaluated by applying the minimum operator to the membership functions calculated in the training phase:
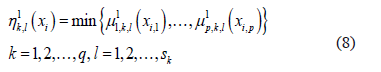
Next, the degrees of membership to each sub-class are combined, resulting in a degree of membership to each class 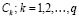 as follows:
as follows:
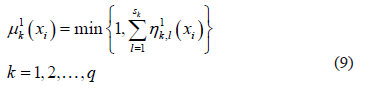
The element  is allocated to the class for which its degree of membership is highest.
is allocated to the class for which its degree of membership is highest.
2.2 The non-parametric fuzzy supervised classification method
The fuzzy pattern-recognition multidensity method described above estimates, in the learning stage, probability functions from the histograms calculated with the values  of the training set elements
of the training set elements 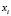 allocated to the sub-classes
allocated to the sub-classes 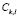 . Although the use of the histogram is very convenient for graphically representing the empirical distribution of frequencies, it has some drawbacks as a method for estimating the theoretical distribution of frequencies. For continuous variables, kernel density estimation methods are often preferable.
. Although the use of the histogram is very convenient for graphically representing the empirical distribution of frequencies, it has some drawbacks as a method for estimating the theoretical distribution of frequencies. For continuous variables, kernel density estimation methods are often preferable.
The kernel density estimators belong to a class of estimators called non-parametric density estimators. Unlike the parametric estimators, which require a fixed functional form, the non-parametric estimators do not have a fixed structure but depend exclusively on the set of observations for the density being estimated. (See Härdle et al. [14] for a detailed explanation of these methods.)
The rationale behind the use of the non-parametric statistical techniques can be found in the fact that the width and the initial points of each histogram bar needs to be determined when calculating a histogram; however, this leads to a problem in that the histograms depend on parameters that are often selected arbitrarily. These drawbacks inspired the development of the first kernel estimators [14].
Therefore, applying a kernel density estimator, the elements in the training sample can be used in order to non-parametrically estimate the density function of the variable 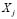 for a sub-class
for a sub-class 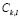 :
:
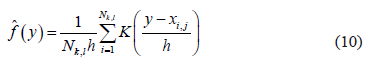
where 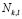 represents the number of elements in the training sample allocated to sub-class
represents the number of elements in the training sample allocated to sub-class 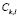 ,
, 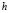 is the smoothing parameter, and
is the smoothing parameter, and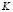 is the kernel function. This function should confirm that
is the kernel function. This function should confirm that 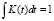 in order to ensure that the density function
in order to ensure that the density function 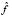 integrates to 1 and where the kernel function K is usually chosen to be a smooth unimodal function with a peak at 0.
integrates to 1 and where the kernel function K is usually chosen to be a smooth unimodal function with a peak at 0.
Note that, in order to eliminate dependence on the initial points of the bins, kernel estimators centre a kernel function at each data point and smooth out the contribution of each observed data point over a local neighbourhood for that data point. The extent of this contribution is dependent upon the shape of the kernel function adopted and the smoothing parameter.
Implementation of this variant in the training process gives rise to 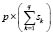 density functions from which the fuzzy membership functions are deduced, using either of two alternatives: discretize the estimated density function
density functions from which the fuzzy membership functions are deduced, using either of two alternatives: discretize the estimated density function 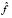 and apply a probability-possibility transformation similar to that referred to above, or implement a continuous probability-possibility transformation using one of the procedures described in Dubois et al. [11]. Obtained in both cases are
and apply a probability-possibility transformation similar to that referred to above, or implement a continuous probability-possibility transformation using one of the procedures described in Dubois et al. [11]. Obtained in both cases are 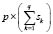 membership functions, which we can now denote as:
membership functions, which we can now denote as:
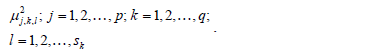
In the nonlinear classification rule, the membership functions 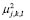 are evaluated in the coordinates of the elements of the test set, resulting in the classification functions
are evaluated in the coordinates of the elements of the test set, resulting in the classification functions 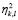 and
and 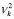 , and in a procedure that is identical to that described in the previous section.
, and in a procedure that is identical to that described in the previous section.
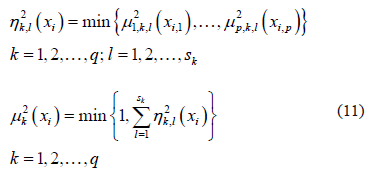
2.3 The data
With a view to conducting a comparative study, the two classification methods were applied to a set of real data. The data used for the application of these techniques were obtained from analyses of samples taken from a primary kaolin deposit in one of the most important kaolin mining areas of Galicia (NW Spain), namely, Vimianzo (A Coruña). The samples were wet-sieved and mineralogical and chemical analyses were performed for 50m-grained fractions following standard procedures. The following information was obtained from the analyses: mineralogical data (percentages of quartz, mica, feldspar, and kaolinite), chemical data (SiO2/Al2O3 ratio, percentages of Fe2O3, TiO2, K2O, MgO, and loss on ignition [LOI]. These parameters are those typically used to identify the suitability of a sample for use in ceramics manufacturing.
All the parameters (p = 10) were selected as variables to which the techniques apply. For each variable, three quality classes were defined—top quality, medium quality, and poor quality [16]—, according to quality rankings as determined in the literature for the ceramic industry [17,18]. In addition to these numerical variables, a ceramic quality variable was included, also defined in terms of three classes reflecting the saleability of the sample—top quality, medium quality and poor quality.
Ceramic quality was evaluated for 1410 samples on the basis of these mineralogical, chemical, and physical parameters. The sample was divided into a training set (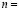 558) and a test set. The number of classes considered for the classification of the sample elements was
558) and a test set. The number of classes considered for the classification of the sample elements was 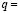 3, in accordance with the ceramic quality grades (top, medium, and poor) defined above.
3, in accordance with the ceramic quality grades (top, medium, and poor) defined above.
2.4 Results
Figure 1 shows the histogram of the kaolin percentage values corresponding to one of the sub-classes in which the medium quality class was divided. Superimposed on the histogram is the membership function obtained by the supervised fuzzy classification method.
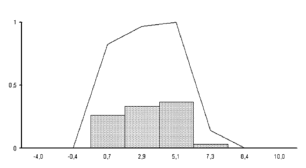
Figure 1. Histogram and membership function were the supervised fuzzy classification method applied to the kaolin percentage variable (x-axis) and one of the medium quality sub-classes for ceramics
The fuzzy classification method implemented in this research used the density of a Gaussian distribution as the function 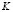 . The smoothing parameter
. The smoothing parameter 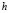 was chosen using the smoothed bootstrap method proposed by Cao [19]. This method for selecting the parameter is particularly suitable when working with independent samples. It was found that greater percentages of correct classifications were obtained using half of the smoothing parameter.
was chosen using the smoothed bootstrap method proposed by Cao [19]. This method for selecting the parameter is particularly suitable when working with independent samples. It was found that greater percentages of correct classifications were obtained using half of the smoothing parameter.
Figure 2 shows the density function when estimated non-parametrically and, for the same variable and sub-class, the membership function obtained by means of the non-parametric fuzzy classification supervised methods.
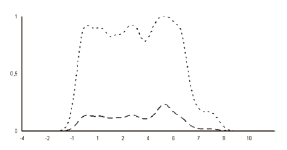
Figure 2. The non-parametric density estimation (broken line) and the membership function obtained by the non-parametric fuzzy supervised classification method (dotted line) for the kaolin percentage variable (x-axis) and one of the medium quality sub-classes
The percentage of correctly classified elements in the training set was 99.64 % for the fuzzy supervised method and 99.82 % for the non-parametric method, whereas the same percentages of the validation test set were 98.01 % and 99.10% , respectively.
3. CONCLUSIONS
This article describes a non-parametric fuzzy classification method that is a variant on the fuzzy pattern matching multidensity method. The difference between the two approaches lies in the method for determining the density function; our method uses the histogram of the data, whereas the multidensity method uses a kernel function. The main advantage of the non-parametric method is that it does away with some of the drawbacks associated with the construction of the histogram, such as the problem of defining the width and initial point for each interval in the histogram.
Our method was tested in determining the quality of kaolin samples obtained from a kaolin deposit for ceramic manufacturing purposes. The level of correct classification was quite similar for both methods, although there was a slight improvement in the fuzzy classification methods.
As future research, we will explore the possibility of automatically selecting the smoothing parameter so that the non-parametric fuzzy supervised classification method becomes genuinely competitive with that proposed by Devillez [7].
ACKNOWLEDGMENTS
This research has been partially supported by grant PGIDIT06PXIC300117PN of the Xunta de Galicia and also by grant PGIDIT07PXIB300191PR of the Xunta de Galicia for the first author.
REFERENCES
[1] Härdle, W., Multivariate Statistical Analysis, Springer, Berlin, 2003. [ Links ]
[2] Izenman, A.J., Modern multivariate statistical techniques regression, classification and manifold learning, Springer, New York, 2008. [ Links ]
[3] Jiménez, C., Soto, C. Aprendizaje supervisado para la discriminación y clasificación difusa, Dyna 169, pp. 26-33, 2011. [ Links ]
[4] Zadeh, L.A., Fuzzy sets, Information and Control, 8, pp. 338-353, 1965. [ Links ]
[5] Kuncheva, L.I., Fuzzy classifier design, Physica Verlag, 2000. [ Links ]
[6] Dumitrescu, D., Lazzerini, B. and Jain, L.C., Fuzzy sets and their application to clustering and training, CRC Press, Boca Raton, 2000. [ Links ]
[7] Devillez, A., Four fuzzy supervised classification methods for discriminating classes of non-convex shape, Fuzzy sets and systems, 141(2), pp. 219-240, 2004. [ Links ]
[8] Dubois, D., Prade, H. and Testemale, C., Weighted fuzzy pattern matching, Fuzzy sets and systems, 28(3), pp. 313-331, 1988. [ Links ]
[9] Pedrycz, W. and Vulkovich, G., Fuzzy clustering with supervision, Pattern Recognition, 37(7), pp. 1339-1349, 2004. [ Links ]
[10] Bezdek, J.C., Erlich, R. and Full, W., FCM: The fuzzy c-means clustering algortihm, Computers and Geosciences 10(2), pp. 191-203, 1984. [ Links ]
[11] Minasny, B. and Mc Bratney, A.B., FuzME version 3.0, Australian Centre for Precision Agriculture, The University of Sydney, Australia, 2002. [ Links ]
[12] Dubois, D., Fulloy, G., Mauris, H. and Prade, H., Probability-possibility transformations, triangular fuzzy sets and probabilistic inequalities, Reliable Computing 10, pp. 273-297, 2004. [ Links ]
[13] Dubois, D. and Prade, H., Théorie des possibilities, Application à la représentation des connaissances en informatique, Masson, Paris, 1987. [ Links ]
[14] Härdle, W., Müller, M., Sperlich, S. and Werwatz, A., Nonparametric and semiparametric models, Springer, New York, 2004. [ Links ]
[15] Parzen, E., On estimation of a probability density function and mode, Annals of Mathematical Statistics 33(3), pp. 1065-1076, 1962. [ Links ]
[16] Taboada, J., Rivas, T., Araujo, M. and Argüelles, A., A fuzzy expert system application to the evaluation of ceramic- and paper-quality kaolin. Applied Clay Science, 33, pp. 287-297, 2006. [ Links ]
[17] Prasad, M.S., Reid, K.J. and Murria, H.H. Kaolin: processing, properties and applications. Applied Clay Science, 6-3,4, pp. 87-119, 1991. [ Links ]
[18] Konta, J., Clay and man: clay raw materials in the service of man, Applied Clay Science, 10(4), pp. 275-353, 1995. [ Links ]
[19] Cao, R., Bootstrapping the Mean Integrated Squared Error, Journal of Multivariate Analysis 45(1), pp. 137-160, 1993. [ Links ]














