Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.79 n.171 Medellín jan./fev. 2012
CONTACT NOTCH STRESS ASSESSMENT WITHIN FRICTIONAL CONTACT JOINTS
EVALUACIÓN DE ESFUERZOS PICO DE CONTACTO EN UNIONES DE CONTACTO Y FRICCIÓN
DARIUSZ SZWEDOWICZ
PhD, Department of Mechanical Engineering, National Center for Research and Technological Development, CENIDET, d.sz@cenidet.edu.mx
JORGE BEDOLLA
PhD, Department of Metal Mechanics, Apizaco Institute of Technology, ljbedolla@itapizaco.edu.mx
Received for review: January 27th, 2010; accepted: December 3rd, 2010; final version: December 21st, 2010
ABSTRACT: Stress concentrations at the ends of a flat contact including frictional sliding are analyzed in this article by using the finite element (FE) method. The numerical studies are conducted with a shaft coupled to the hub by conical rings. The applied mesh refinement at the contact ends assures the reliability of the FE results, which show significantly higher stress peaks than those obtained from the conventional analytical solution recommended in the design guidelines of the frictional conical joints. These notch stresses result in low cycle fatigue (LCF) failures of the shaft-hub connection in service, since the yield point of the shaft material can be locally exceeded. The effect of clearances among the joint components and magnitudes of the friction coefficient on variations of the maximum stress in the contact are considered as well. The paper's findings and conclusions are applicable to the design and manufacturing process of the frictional conical joints with regard to assembly tolerances.
KEYWORDS: contact stress concentration, finite element method, mechanical joints, shaft
RESUMEN: En el artículo se analizan, por medio del método del elemento finito (FE), las concentraciones de esfuerzo en los límites de zonas de contacto nominales que incluyen deslizamiento con fricción. Los elementos mecánicos para el análisis numérico se consideran como una flecha acoplada a un cubo de rueda por medio de aros cónicos deformables. El proceso de refinamiento de malla usado en el modelo discreto garantiza la confiabilidad de los resultados de FE, los cuales muestran un pico de esfuerzo considerablemente mayor al obtenido de la solución analítica, que usualmente se recomienda en guías de diseño de uniones con fricción. Esos picos de esfuerzo resultan en fallas por fatiga de bajos ciclos (LCF) durante el servicio de la unión flecha cubo, porque pueden rebasar el punto de cedencia del material en áreas particulares de la flecha. Además en el estudio se considera el efecto de claros y magnitudes de fricción, entre los componentes mecánicos, y su influencia en la variación del esfuerzo máximo de contacto. Los resultados y conclusiones obtenidos del artículo son aplicables a los procesos de diseño y manufactura de uniones cónicas con fricción, con relación a sus características y tolerancias de ensamble.
PALABRAS CLAVE: concentraciones de esfuerzo de contacto, método del elemento finito, uniones mecánicas, flecha
1. INTRODUCTION
Considering uniform stress distribution over contact regions of the shaft and hub, a component's lifetime can be predicted properly by using analytical methods in the assembly of mechanical components, particularly in couplings with positive press. In real contact, stress concentrations appear in regions determined by the geometrical forms of contact elements. The dissimilarities in the real dimensions of the assembled parts [1] can produce bending moments, and concentrated forces acting on the conical rings. The stress concentration in mechanical assemblies is a factor which accelerates the failure process of the parts [2]. In the shaft and hub connection arranged by a press fit, the prediction of an accurate stress distribution helps to improve its coupling performance [3]; nevertheless, due to the physical nature of contact couplings with the positive assembly pressure, stress concentrations always occur in assemblies with deformable elements [4,5].
Demands in increasing power densities in drive trains place growing requirements on shaft-hub connections [6]. From all engineering considerations, the coupling joint's performance and uniform stress distributions within the assembled components are two major features in the free-of-failure design of the shaft-hub connection. The determination of the real stress distribution and local peak contact stresses value in the contact regions contributes considerably towards the mitigation of risk in failure appearances. Uniform stress distribution prevents significant strain differences within the contact regions of the assembled parts which is reflected through the longer lifetime of working parts. Regarding the low cyclic fatigue (LCF), an allowable small difference of alternating stresses between the standstill and service condition contributes to the reduction of relative slip amplitudes of coupled parts. The prediction of the allowable small alternating tangential strains on contacts allows for the avoidance of wear, which frequently initiates failure during the operation. This phenomenon, called fretting, has been studied experimentally and numerically by several authors [7-11]. However, the general design criterion, which definitively determines a technical manner to prevent fretting, is still not available in the literature. Anyhow, the ordinary design principal of holding onto the maximum local stress below the ultimate stress remains an important issue in the designing of mechanical joints.
From the conventional design point of view, a technical improvement in more coherent stress distribution can be the press fit used in the assembly of the shaft and hub by applying conical frictional rings at the joint. A typical conical friction joint is shown in Fig. 1. Its major advantages are as follows [12]: a) the montage capabilities in easy assembly and disassembly do not require special caution in precise axial positions of the hub to the shaft; b) the low costs of the rings; c) the joint provides an additional sealing capability, and d) the joint provides a control of shaft overloading with regard to the threshold friction force.
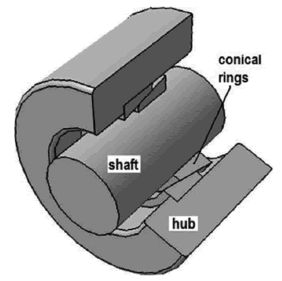
Figure 1. Basic components of the shaft-hub connection with conical rings
The frictional shaft and hub connection including the conical rings allow for an extension of the usefulness of the life of mechanical components [12]. However, this statement is based on the contact mechanics of rigid rings, being that they are an assumption of the analytical solution. Elastic deformations of the conical rings, which are neglected in traditional analytical equations, introduce stress concentrations at the ends of the contacts between the rings, the upper ring to the hub and the lower ring to the shaft [13]. At these regions, relatively small volumes of the material can be highly overloaded above the allowable stress, which assures free-of-failure operation [14].
The assembly between the rings is established by the contact press, which is commonly determined by using traditional analytical formulas. The numerical methodology developed here specifies local stress concentrations on contacts of the shaft, the hub and the rings, that are used in one frictional joint. Also, increasing in contact stress peak value such as the modification of contact area between shaft and ring is analyzed. Due to diameter differences in the shaft's outer contour and the hub's inner contour, the maximum frictional force is expected to occur on the shaft. The proposed numerical approach is based on the finite element analysis by using the ABAQUS FE system. This discrete model includes different clearances between the shaft and the inner ring. The FE results obtained show that variation of clearances in the joint makes an impact on the effective contact area. To compensate for this incapacity of joint coupling, the increase of contact force can be considered. With respect to the yield stress of the used materials, the comparison of the numerical results with the analytical solution shows that the conventional theory overestimates the effective contact length and underestimates the real contact press in the joint considered for its nominal dimensions.
2. CONTACT PRESSURE OF SHAFT- HUB CONNECTION
In the present study, maximum stresses on the contact of the shaft, which is coupled by conical rings to the hub, are analyzed in detail. The typical conical friction joint contains the shaft, the hub, the inner, and the outer conical ring. To increase joint capability, more pairs of the conical rings are usually used in engineering practice. However, since essential analysis is the same for every pair of rings, in this work only a pair is considered. Taking into account this configuration with contacts including friction, the numerical non-linear approach, based on the finite element method, has to be used in the simulation of elastic material behavior. For the modeling of one joint, three contact surfaces located between the rings, between the outer ring and the hub, and between the inner ring and the shaft are simulated by assuming constant friction coefficient.
To obtain the coupling (see Fig. 2), displacement of the outer ring is constrained in the axial direction. Then an assembly axial load P is applied axially upon one side of the inner ring. The assembly load P deforms the conical rings and produces contact press W1 and W3 in a radial direction, as well as reaction force F in axial direction (Fig. 2). In function of the acting radial contact press, friction forces appear on the contacts which limit relative motion between assembled components. The equilibrium contact state determines the coupling capability for transmitting axial load and torque. The press load over the rings, the mechanical properties of the material used, the geometry of the mechanical elements, the contact angle and friction coefficients, establish the resulting capabilities of the mechanical joint. In addition, initial clearances between the contact surfaces influence the effective contact pressure and size of contact region over the shaft and hub. These clearances are a result of the machining process. In real applications, clearance effects need to be considered in the design, because it could considerably modify the final performance of mechanical assembly.
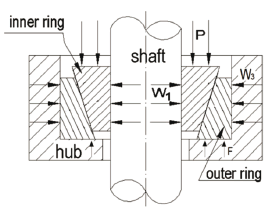
Figure 2. Contact press acting on the conical rings
To take these clearances into account, the entire numerical analysis of the joint assembly is performed sequentially. First, a fraction Po of the press load P is imposed on the inner ring to eliminate initial clearances. Then the press load PA (the complement of P) is applied to produce the effective contact assembly between the shaft and the hub [15] through the conical frictional rings. Considering that the primary role of the analyzed joint is to transmit the maximum torque from the shaft to the hub, the highest pitch of frictional forces on all contact surfaces (Fig. 2) is required from a design point of view.
Following the analytical model, neglecting elastic deformations, forces acting upon the inner ring are shown in Fig. 3. Component forces P and Q on conical surface can be transformed into T2 and W2 in axial and radial direction respectively, by Eq. (1) (Fig. 3b).
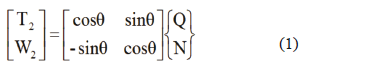
where: T2 and W2 are the force components in the axial and radial direction, respectively; q is the conical inclination, Q is the friction force on the conical region, N is the normal force. The forces W2 and W1 are considered to be equal to each other in order to maintain equilibrium on the inner ring. The normal contact force W1 acts upon the contact region between the shaft and the inner ring and produces the contact stresses on the shaft. Frictional force over the shaft contact region is a function of the normal contact force W1 and the friction coefficient m. From Fig. 3b it can be seen that:

where: q is the conical inclination, ρ is the friction angle (ρ = atan-1 m), m is the friction coefficient, T2 and W2 are the force components in the axial and radial direction, respectively.
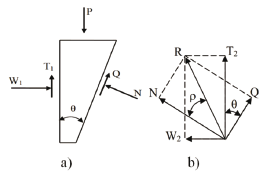
Figure 3. Forces acting on the inner ring, where: a) force directions and b) force transformation
Considering the same friction coefficient for all contact surfaces, force equilibrium and W1 = W2, and according to the free body diagram shown in Fig. 2 and Fig. 3 we have:

where: Ti and Wi are the force components in the axial and radial direction, respectively, ρ is the friction angle, P is the press load, and F is the reaction force.
Substituting Eqs. (2) and (3) in (5), and considering tanq • tanρ @ 0, W1 can be expressed by

where: W1 is the force component in the radial direction, PA is the press load fraction to produce the shaft-hub connection, q is the conical inclination, m is the friction coefficient. This is consistent with simplifications presented by [16].
If there are no initial clearances in the system among the rings, the hub and the shaft, Po is omitted and the assembly load is determined by P = PA. This assembly load is usually arranged by axial screws, which induce the resulting axial pressure P on the front side of one ring as is illustrated in Figs. 2 and 3. If mechanical clearances appear in the assembly, a part Po of the assembly load P is used to eliminate initial gaps. Then, the joint is effectively assembled by the load P = PA + Po. Higher magnitudes of the initial clearance decrease contact press PA in Eq. (6), and then the value of the normal contact force W1 becomes smaller. Although the reaction normal contact forces W1 and W2 are considered to be equal to each other to keep the inner ring in equilibrium. In fact, local elastic deformations of the rings have influence over contact stress distributions in the whole system. It is further presented by the modeling of the system with the finite element method, where local deformations produce a significant variation of contact pressure along axial direction over shaft and hub.
3. NUMERICAL MODEL
Constant pressure distribution due to W1 over the contact region of the shaft in Eq. (6) is a simplification of the contact force. It is commonly considered in the practice of design to estimate the characteristics of a friction joint. However, contact pressure in a joint with conical elements is not a constant. Therefore, a discrete model of the frictional joint, which includes local deformation, is developed in order to analyze rings' local deformations and stress concentrations along contact on shaft in axial direction. The following analysis is based on a shaft nominal diameter of 20 mm and a hub internal diameter of 25 mm. The selected axial length of both inner and outer ring is equal to 5.3 mm. After their assembly the total axial length of the ring' pair equals 6.3 mm and the nominal half conic angle of both rings is q = 16.7 deg (see Fig. 4). The rings RfN S8006 (20 x 25 mm) are made according to the material properties and geometry characteristics given in [12]. The fit between the inner ring and the shaft is arranged by E7/h6, and between the outer ring and the hub it is determined with H7/f7 [12]. Taking into account the components' diameters and their fits, the maximum clearance between the shaft and the inner ring is cmax = 0.074 mm, and the maximum clearance between the hub and the outer ring equals 0.062 mm. The shaft material is steel AISI 4140, annealed at 815 ºC, air cooled, with a Young modulus of 210 GPa, and a yield stress of 420 MPa.
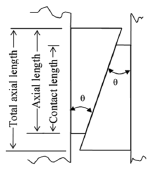
Figure 4. Contact geometry of conical rings
A finite element model is built using the Abaqus FE software. Four finite element meshes of the shaft, hub, and both rings are dissimilar on three contact surfaces. The symmetrical character of the joint is properly modeled by axsymmetric linear finite elements CAX4 y CAX3. Assuming small deformations, formulation for small sliding contact is used for simulating open contact state, sticking, or sliding contact behavior on contact surfaces. After non-linear iterative solutions of the static contact equations [17], the final FE contact results contain the information about normal and tangential contact forces as well as clearances or overlapping magnitudes at all nodes representing the contact surfaces. Considering friction effects and fine contact meshes, the contact FE analysis is performed in a reliable manner. For the alloys analyzed, a friction coefficient of 0.12 is applied. The contact formulation is based on Amonton's law. Six different initial clearance ratios (c/cmax) between the inner ring and the shaft are used: 0 (ideal case, no gap), min, ¼, ½, ¾, and 1. The contact surfaces of the shaft and hub are considered to be smooth. In this way, neither roughness nor waviness are simulated.
The discrete model of the mechanical joint is shown in Fig. 5. By creating the FE meshes of the shaft, the hub and the rings, particular consideration is focused at the mesh refinement of the contact regions. The generated fine contact meshes allow for reliable simulation, which is described in the FE result by the contact area [13], reaction forces, clearances, and overlapping as well as by the normal and shear stresses.
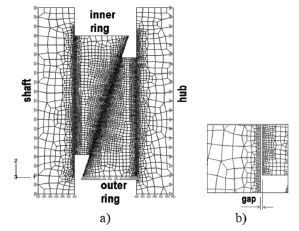
Figure 5. Finite element model, a) four dissimilar meshes of the components with the boundary conditions shown, b) zoom pointing out the gap between the shaft and the inner ring
For the study, the outer conical ring is fixed on its bottom side by constraining the nodal axial movement (see Figs. 5 and 2). The nodes on the contour sides of the shaft and the hub also are constrained to fix their axial movement. The size of mechanical components presented in Fig. 5 corresponds to a transversal section of a mechanical joint. To consider the material of shaft and hub and its corresponding stiffness complementary, constrains in radial direction were added, as shown in Fig. 5. It is clear that this consideration increasing stiffness of shaft and hub; however, preliminary tests with complete geometry were carried out, whose results indicated insignificant variation on contact press. The major variation was in the corner of conical surfaces and was around 10% higher than results obtained with the model in Fig. 5. Afterwards, the results obtained from this model were considered to be adequate.
Nodal constrains and contact pairs, defined on the contact surfaces, prevent rigid body motion in the FE simulation. The imposed boundary conditions allow for the axial movement of the inner ring up until the elimination of clearances. Then they were obtained for the elastic deformations of all meshes in contact. The press load P is applied to the upper side of the inner ring. The non-linear FE computation in terms of clearance and friction iteratively simulates the entire process. After the elimination of gaps, press load P produces the radial deformations of the rings, which couple the shaft and hub together. Frictional forces determine the maximum torque and axial load that can be transmitted from the shaft to the hub. Simulations take into account the elastic deformations of the rings, which are not considered in the conventional theory.
Press load P applied to the inner ring is defined by fraction Po for elimination of gaps in the system, and PA for the effective coupling of the shaft to the hub. The magnitude of the press load is determined according to [12]. In the first analysis, the coupling performance is calculated by neglecting initial clearances and the magnitude of the press load (P = PA) is equal to 18 kN [12]. This analytical calculated coupling provides the maximum normal contact force by getting the maximum contact area between the shaft and hub. However, this contact area does not correspond to the axial length of the inner ring. The second analysis is performed for a constant press load of P = Po + PA = 30.5 kN [12], and six different clearances (gaps), which are given by c/cmax = 0 (ideal case, no gap), min, ¼, ½, ¾, and 1. For these conditions, the contact area is reduced increasing initial clearances, and remaining, the normal contact force W1 equals 33.3 kN. For the third analysis, the contact area between the shaft and hub is kept constant, and the press load is increased which is what induces a growth of peak values of the contact stresses. The trial and error procedure is developed in order to reach it, because the contact area is not directly proportional to the press load.
4. RESULTS AND DISCUSSION
Stress concentrations are the results of the non-uniform normal pressure distribution over the shaft due to the elastic local deformations of the inner conical ring. The FE results show that the peak values of the contact stress can be several times higher than that which is calculated by the conventional theory, which determines the normal contact stress average. Consequently, the maximum contact stress located at contact ends over a small region is underestimated by the conventional theory, and it can be a reason for initiation failure.
The first analysis for the load scheme (without clearances, ideal case) assumes that the whole cylindrical surface of the inner conical ring must be initially in contact with the shaft, and the contact pressure would be uniformly distributed. Figure 6 shows the results of the contact length and contact pressure on the shaft for a press load of 18 kN and without initial clearances. In Fig. 6, the curve called Ideal case, relates to the FE results simulated without clearances, this curve is evaluated along the contact contour of the shaft, whose length is smaller than the axial length of the conical ring. According to Eqs. (1), (6), (7), and reference [12] the average contact press on the shaft is 100 MPa, distributed on the nominal contact area.
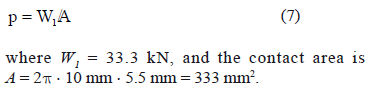
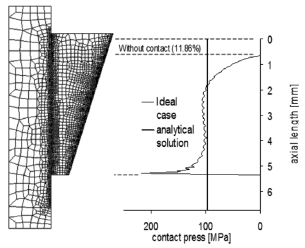
Figure 6. Contact press over the shaft for the frictional joint without initial clearances
However, the maximum contact press, from the FE results (ideal case), is more than two times higher (221%) in relation to the analytical solution. This maximum FE stress is located at a small area of about 9.4 mm2. In general, the FE results are slightly higher than an analytical value of 100 MPa. This indicates that a small contact region where the crack nucleation by cyclic LCF loading can begin, exists. In addition, the FE contact area is smaller than the analytical result. For the current study, the shaft has a nominal diameter of 20 mm and the inner ring has an axial length of 5.3 mm. These dimensions of the components must generate a contact area of 333 mm2, but for the first loading case analyzed (Figs. 6 and 7) the contact is 11.86% smaller than that from the analytical solution.
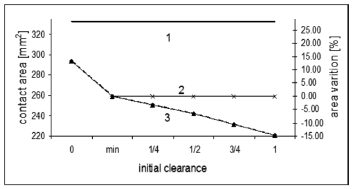
Figure 7. Variation of the contact area, where (a) full contact (theoretical case), (b) constant area (is controlled by increments of press load P), and (c) variable contact area is a function of the initial gap size (P is constant)
The second case analyzed corresponds to the assembly condition with the constant press and variable initial clearances. For a nominal diameter of 20 mm, the fit between the shaft and the hub must be defined with E7/h6 [12]. Then, radial gaps used for ratios c/cmax = 0 (no gap), min, ¼, ½, ¾, and 1, are equal to 0 mm, 0.020 mm, 0.024 mm, 0.029 mm, 0.033 mm, and 0.037 mm, respectively. As in the first analysis, the maximum contact stress and area modifications are of interest in the simulation. For fit E7/h6, the analytical contact pressure over the shaft must be equal to 100 MPa, which is considered to be the constant value independent from the gap magnitude [12]. From Eqs. (1) and (6), the average contact pressure on the shaft might be 100 MPa, like the uniform stress distribution along the contact. Indeed, this analytical solution differs significantly from the numerical results. For the same reason, the apparent contact area decreases in comparison with the theoretical estimation (nominal area), if a gap increases between the components. For the assembly condition without initial gaps, the contact area is reduced by applying the press load. This implies that the analytically and numerically predicted contact areas differ from each other in terms of the gap magnitude.
Figure 7 shows the contact area variations with respect to the constant press and incremental press load. Increasing press load allows us to maintain the same contact area as the reference area. The analytical nominal contact area overestimates the apparent contact area, which in reality depends on elastic deformations of the components. To establish the ratio of the area reduction, the minimum radial gap is applied to fit E7/h6, and its calculated contact area is considered to be the reference result (see “min” in Fig. 7). For this fit, the design recommendation [12], which neglects the presence of clearance in the joint, is taken into account and the contact press load P of 30.5 kN and the assembly contact press PA of 18 kN are used in the simulation. For these loads, the contact area reduces with a growth of the initial clearance, as is shown in Figs. 7 and 8 as well as in Table 1. This reduction of the apparent contact area, reaches 15% in the case of the maximum gap, and even increases to 45%, since the ideal contact configuration between the rings (Fig. 7) is considered to be the reference. At the contact ends, the stress concentration is 300% higher than the analytical value. Outside the contact ends, the numerical contact stresses correspond to a constant stress distribution along the contact, as it is predicted analytically. According to Eq. (6), for the second analyzed case, the normal contact force W1 is equal to 33.3 kN, which is obtained for the contact press of 100 MPa. Finally, it can be noticed in the computed stress distribution, that the peak stress value with its rapid gradient is located in a narrow range of 0.1 mm of the axial length. This region has to be treated as a risk area of possible LCF failures.
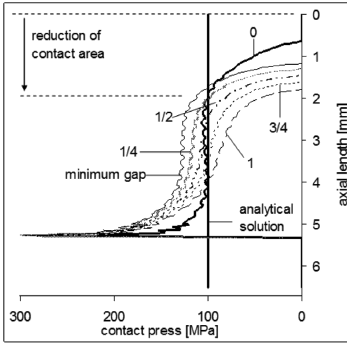
Figure 8. Contact press on the shaft (case-constant press load P)
Table 1. Variation of the maximum contact press (case-constant press load P)
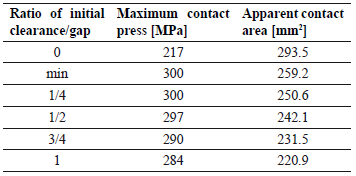
The results of the previous analysis indicate quite clearly that by the acting of the constant press load clearances the final characteristic of the joint is modified, which cannot be expected from the analytical solution. Although the peak press value remains practically constant (see Table 1), distributions of the contact stress along the contact area vary significantly. This stress variation decreases the effective contact area indirectly proportional to the clearance value (see Fig. 8). As a consequence of this phenomenon, the frictional force reduces in the inverse ratio to the gap. Then the maximum torque considered for the transmission at the joint decreases as well.
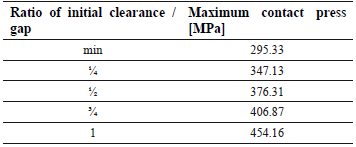
By the presence of the constant clearance, the constant contact area, as expected in the analytical solution, but increasing the clearance the constant area can be achieved by applying higher press load. A third analysis case is arranged in order to obtain a constant contact area of 259.2 mm2, which corresponds to the minimum clearance in fit E7/h6 (see Fig. 7 and Table 1). Since there is no linear relationship between the press load and the contact area due to non-linear contact behavior in numerical simulations the trial and error procedure is used. To always get the same contact area, magnitudes of the applied contact presses, which compensate the presence of different gap clearance, are shown in Figs. 7 and 9. The increase of the press load induces higher peak stress values too, which is the physical consequence for a risk of LCF failures in these contact regions which implies that if the mechanical joint (analyzed statically) is used with alternating loads, LCF is a possibility due to peak stress. In the simulation, the nominal geometry of the component is considered and the aging effect is not taken into account in the analysis. Thus, the theoretical contact press always is the same in the cases considered, which is represented by a vertical line in Fig. 9. For the third case analyzed, the stress peaks at the contact ends, as well as the stresses on the rest of the contact, always are higher than that those obtained from the analytical solution (see Fig. 9 and Table 2). This means that the analytical press contact is underestimated and the strength of the shaft material must be higher than the one calculated by conventional theory than that which is determined according to the conventional theory usually used in the design of frictional joints. As can be seen from Fig. 9, the peak value of the contact stress for the maximum gap is about 454% higher in comparison to the analytical value.
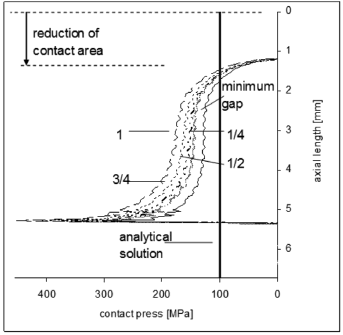
Figure 9. Press contact on the shaft (case-constant contact area of 259.2 mm2)
Table 2. Variation of the maximum contact press (case constant area)
5. CONCLUSION
According to the FE results of all the cases analyzed, the contact stress is underestimated by the conventional theory, whereby the contact area is overestimated. In addition, the peak value of the FE contact stress is 2 to 3 times higher than the analytical contact stress. In the engineering practice, a factor δ of 3 can be used as the notch contact factor in the estimation of the maximum stress smax. Then, the maximum contact stress can be obtained from multiplying the average analytical stress sanly by the notch contact factor δ. Of course this notch contact factor depends also on the materials used and the geometry of the joint. By repeating the finite element procedure presented in this work, this notch factor can be determined anew.
In general, the shaft-hub connection with conical rings has the possibility of improving the contact stress distribution on the shaft. Indeed, it requires geometry modifications of the contact contours, but the contact optimization was beyond the scope of this research. The proposed FE computational procedure permits the shape optimization of the components, which either reduces or might eliminate the high stress gradient in the contact, what would mitigate the risk of the initiation of mechanical failures by fretting, pitting, or wear.
6. ACKNOWLEDGMENTS
The present work was supported under grant No. CONACyT 102025.
REFERENCES
[1] Gómez, J., Romero J., Una mirada a las normas sobre dimensionado y tolerado geométrico en Hispanoamérica. Dyna, 153, pp. 7-18, 2007. [ Links ]
[2] Baragetti, S., Terranova, A., Effects of over - torque on stress relief in conical threaded connections. Journal of Mechanical Design, 126, pp. 351-358, 2004. [ Links ]
[3] Baldanzini, N., A general formulation for designing interference - fit joints with elastic plastic components. Journal of Mechanical Design. 126, pp. 737-743, 2004. [ Links ]
[4] Dhufia, J., Powalka, B., Ulsoy, A., Katz, R., Effect of a non linear joint on the dynamic performance of a Machine tool. Journal of Manufacturing and Science Engineering, 129, pp. 943-950, 2007. [ Links ]
[5] Suaréz, F., Vélez J., Una herramienta matricial para el modelado en 2-D de algunos problemas de contacto elástico, Dyna, 156, pp. 195-206, 2008. [ Links ]
[6] Grossman, C., Fretting fatigue of shape optimised polygon-shaft-hub connections. Ph. D. thesis, Berlin University, 2007. [ Links ]
[7] Baek, D., Khonsari, M., Friction and wear of a rubber coating in fretting. Wear 258, pp. 905-912, 2005. [ Links ]
[8] Gallego, L., Nélias, D., Jacq, C., A comprehensive method to predict wear and to define the optimum geometry of fretting surfaces. Journal of Tribology, 128, pp. 476-1785, 2006. [ Links ]
[9] Gessesse, Y., Attia, M., Osman, M., On the mechanics of crack initiation and propagation in elasto-plastic materials in impact fretting wear. Journal of Tribology, 126; pp. 395-403, 2004. [ Links ]
[10] Mcveigh, P., Farris, T., Finite element analysis of fretting stresses. Journal of Tribology, 119, pp.798-802, 1997. [ Links ]
[11] Vingsbo, O., Söderberg, D., On fretting maps. Wear, 126, pp. 131-146, 1998. [ Links ]
[12] RINGFEDER. catalog E - 12 - 01 RfN 8006, (Ringfeder), 2007. [ Links ]
[13] Szwedowicz, D., Bedolla, J., Experimental and numerical coupling proof of conical joints, Key Engineering Materials, 347, pp. 557-562, 2007. [ Links ]
[14] Hyder, M., Asif, M., Optimization of location and size of opening in a pressure vessel cylinder using ANSYS, Engineering Failure Analysis, 15, pp. 1-19, 2008. [ Links ]
[15] Orlov, P., Fundamental of machine design. MIR Publisher, Moscow, 1980. [ Links ]
[16] Niemann, G., Tratado Teórico -Práctico de Elementos de Máquinas, Cálculo Diseño y construcción, Ed. LABOR S.A. Tr. from "G. Niemman, Maschinenelement. Entwerfen, Berechnen und Gestalten im Maschinenbau. Ein Lehr- und Arbeitsbuch, Ed. Springer-Verlag", 1967. [ Links ]
[17] ABAQUS Ver 6.5, Analysis User's Manual, Volume II: Analysis (Abaqus, Inc), 2004. [ Links ]














