Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.79 n.171 Medellín jan./fev. 2012
DRYING KINETICS OF TWO YAM (Dioscorea alata) VARIETIES
CINÉTICA DE SECADO EN DOS VARIEDADES DE NAME (Dioscorea alata)
RAMIRO TORRES
Magister en Ciencia agroalimentaria, Profesor Asistente, Universidad de Córdoba, Colombia. rtorres@corre.unicordoba.edu.co
EVERALDO J. MONTES
Magister en. Ciencias y tecnología de alimentos, Profesor titular, Universidad de Córdoba, Colombia. everaldomontes@yahoo.com
RICARDO D. ANDRADE
Ph.D. (c) en Ciencia y tecnología de alimentos. Profesor Asociado, Universidad de Córdoba, Colombia. ricardo.andrade@usach.cl
OMAR A. PEREZ
Ph.D. en Ciencias y tecnología de alimentos, Profesor Asistente, Universidad de Córdoba, Colombia, operez@sinu.unicordoba.edu.co
HUGO TOSCANO
Licenciado, Profesor asistente, Universidad de Córdoba, Colombia, utoscano@sinu.unicordoba.edu.co
Received for review February 2th, 2010, accepted February 2th, 2011, final version March, 2th, 2011
ABSTRACT: The aim of this research was the evaluation of the kinetics and the drying conditions, at laboratory scale, of two yam varieties (D. alata 9506-021 and 9506-027) from the germplasm bank of the University of Cordoba (Colombia). Two geometries (circular and square) were used for the study; the air temperature ranged from 40 to 70 °C and the air speed was 0.7 m s-1. The experimental data were fitted appropriately to Fick, Page, and Logarithmic models. Mass transfer of the yam slices was described by using Fick's diffusion model, which was the best fitted model. Drying occurred mainly in the decline phase. Arrhenius described properly the dependency of the moisture diffusivity with temperature. Among the temperature range evaluated, moisture diffusivities varied from 1.70 x 10-9 to 6.84 x 10-10 m2/s and 1.33 x 10-9 to 6.30 x 10-10 m2/s for the D. alata 9506-21 and 9506-27, respectively. The drying activation energy for D. alata 9506-21 and 9506-27 varied from 23.19 to 25.72, and 16.03 to 17.82 kJ/mol, respectively.
KEYWORDS: effective diffusivity, Fick's model, Page's model, activation energy
RESUMEN: El objetivo de esta investigación fue la evaluación de la cinética y condiciones de secado, a escala de laboratorio, de dos variedades del ñame (D. alata 9506-021 y 9506-027) del banco de germoplasma de la Universidad de Córdoba (Colombia). Dos geometrías (circular y cuadrada) fueron utilizadas para el estudio; la temperatura del aire fue variada en un rango entre 40 a 70 °C y la velocidad de aire fue de 0.7 m.s-1. Los datos experimentales se ajustaron apropiadamente a los modelos de Fick, Page y Logarítmico. La transferencia de masa del ñame fue descrita usando el modelo de difusión de Fick's, que fue el modelo que mejor se ajustó. El secado ocurrido principalmente en la fase de decreciente. La relación de Arrhenius describió satisfactoriamente la dependencia de la difusividad de la humedad con la temperatura. Entre el rango de temperatura evaluado, las difusividades de la humedad variaron de 1.70 x 10-9 a 6.84 x 10-10 m2/s, y 1.33 x 10-9 a 6.30 x 10-10 m2/s para D. alata 9506-21 y 9506-27, respectivamente. La energía de activación para el secado de D. alata 9506-21 y 9506-27 varió de 23.19 a 25.72 y 16.03 a 17.82 kJ/mol, respectivamente.
PALABRAS CLAVE: difusividad efectivad, modelo de Fick, modelo de Page, energía de activación
1. INTRODUCTION
Yams (Dioscorea spp.) are an important source of carbohydrate for many people in Colombia, especially in the Caribbean Coast, where 97353 tons were, harvested in 10066 hectares during the year 2005 (DNP, 2006). Yams belong to the genus Dioscorea of the family Dioscoreaceae; which has about 600 species; among them D. alata L.; D. cayenensis Lam, and D. rotundata Poir, have the greatest economic importance (Montes et al., 2009). Yams are widespread and are one of the major staple foods in many tropical countries (Akanbi, Gureje & Adeyemi, 1996; Omonigbo & Ikenebomeh, 2000).
Yam is not considered to be a high-priority product, for this reason, an appropriate technological development has not been presented concerning the production and prosecution of this tuber. Besides its losses during the cultivation and gathering periods, there are also losses between 20 and 30 % during the post harvest because of the methods and infrastructure used are rudimentary. As a result, this leads the investigation into lack and modernization to industrial scale in order to achieve better conservation alternatives, use and decrease of losses (Guzmán & Buitrago, 2000)
Besides a moisture content of between 50 and 80 %, which makes it susceptible to deterioration, yam tubers comprise mainly of fiber, sugars, protein and starch, the last of which is found in the highest proportions (Opara, 1999). To overcome the high perishability of fresh tubers due to the high moisture contents, yams are processed into flour by peeling, slicing, blanching and sun-drying (Akissoe et al., 2001). Drying is a universal method for conditioning foods by the elimination of the water until a level that allows its balance with the ambient air, in such a way that preserves its physical and chemical characteristics (Ruiz & Montero, 2005). The removal of water in the solid foods arises initially, like a form of reduction of the water activity, inhibiting the microbial growth; therefore, it passes to also have significant importance in the reduction of energy costs, of transport, packing and storage of the foods that with high quantities of water (Cardoso, 2004).
Dried and milled yam is less perishable and can be consumed throughout the year, mainly to produce starch (Akingbala, Oguntimehin & Sobande, 1995; Akissoe et al., 2001). Thus the objectives of this research is to investigate the effects of yam variety and processing conditions on the drying characteristics, maximum content of starch and activation energy for drying of the yam their varieties D. alata 9506-021 and 9506-027.
2. MATERIAL AND METHODS
2.1 Drying pretreatments, procedure and conditions
Water yams (Dioscorea alata) were obtained from the germplasm bank from the PBA and University of Cordoba, Colombia. Average moisture content of D. alata was 87.7344 ± 0.2 % (wet basis). Yams were washed, manually peeled and cut into circular and square slices having the dimensions of 3.19 cm of radio and 5.6 x 5.6 cm, respectively, using very sharp stainless steel molds to carry out this procedure.
2.2 Drying procedure
The dryer system consisted of horizontal air flow through trays and was arranged as a closed circuit. For the air heating, three electric resistances were used (two of 1600 W and one of 800 W), which could be worked independently, controlled by a digital thermostat. A thermal-hygrometer (TESTO 635) was used in order to measure the dry bulb temperature as well as the drying air humidity. A digital anemometer (AIRFLOW Co. LCS 6000) was used to measure the drying air velocity (Fig. 1), designed and fabricated at the Department of foods Engineering, University of Cordoba, Monteria, Colombia. Drier was allowed to run for about an hour prior the loading of samples to allow the heated air to stabilize at the desired temperatures (40, 55, and 70 ºC) and at constant air velocity (0.7 m s-1). Samples were loaded into the drier and removed at regular intervals until three consecutive weights were constant, indicating equilibrium condition.
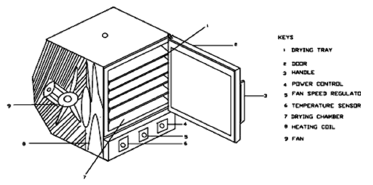
Figure 1. Isometric view of the fabricated air drier used for the drying of yam
Moisture contents at equilibrium were determined according to the method of AOAC (1997). Drying experiments were conducted in triplicate and average values reported.
The drying kinetics was studied by observing the drying curves for the considered air temperature and velocities.
2.3. Determination of drying characteristics
For model evaluation, a nonlinear regression procedure was used, for both models (Eqs. 5 and 6), using the statistical package Statistica 7.0 (StatSoft, Inc 2004). The modelling was characterized by the average relative error E (Eq. 1) calculation and the determination coefficient, R2.
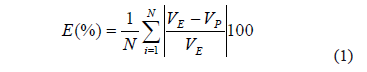
where N is the number of experimental data, VE is the experimental value and VP is the calculated value.
It is generally assumed that the mechanism of moisture migration during thin layer drying of food materials is characterized by diffusion as described by Fick's second law of diffusion (Babalis & Belessiotis, 2004; Doymaz & Shovel, 2002; Luikov, 1966; Maskan, 2001; Saravacos, 1995; Senadeera et al., 2003).
An infinite slab of thickness 2L having the uniform initial water amount, undergoing drying under constant conditions can be described by Fick's unidirectional diffusion equation (Crank, 1975):
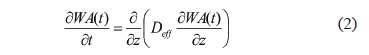
Using the following initial and boundary conditions:
uniform initial amount: 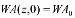
symmetry of concentration: 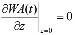 ,
,
equilibrium content at surface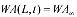
and applying:
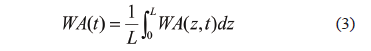
Therefore, the solution as a series obtained for water transport in a cubic solid corresponds to the product of three perpendicular infinite slabs solutions (Crank, 1975; Treybal, 1981):
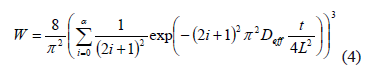
where Deff is the effective diffusivity of water (m2/s), i is the number of series terms, L is the characteristic length, sample half-thickness (m), t is the drying time (s), W is the dimensionless amount of water defined by Eq. (5).
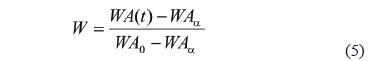
where WA0 is the initial water amount (g), WA∞ is the equilibrium water amount (g) and WA(t) is the average water amount at instant t (g).
Eq. (4) can be used in terms of moisture content:
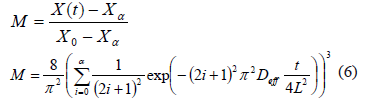
where M is the dimensionless moisture ratio, X0 is the initial moisture content (g water/100 g dry matter), X∞ is the equilibrium moisture content (g water/100 g dry matter), and X(t) is the average moisture content at instant t (g water/100 g dry matter).
One of the most useful empirical models is Page's equation (Page, 1949), which is an empirical modification of the simple exponential model. It is written in the form:
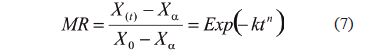
where k is the drying constant, n is the Page's parameter and t is the process time (s).
The empirical logarithmic model is also used as a good approximation to explain the kinetics and drying conditions (Ertekin & Yaldiz, 2004); it is written in the form:
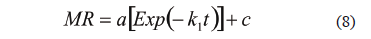
where k1 is the drying constant, a and c are the models parameter and t is the process time (s).
Karatas (1997) and Senadeera et al. (2003) reported the correlation between the drying conditions and the values of the effective diffusivity using Arrhenius type equation:
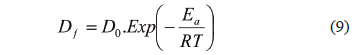
Where D0 is diffusion coefficient; Ea is activation energy (kJ/mol); R is universal gas constant (8.314 J/mol K) and T is absolute air temperature (K).
2.4. Statistical analysis
Results were evaluated for analysis of variance (ANOVA) using Statistica 7.0 (StatSoft, Inc., 2004).
3. RESULTS AND DISCUSSION
3.1 Effect of temperature, geometry and variety on moisture ratio and drying rates of yam.
Figures 2 and 3 show the effect of temperature on moisture ratio of D. alata during air-drying, for varieties 9506-21 and 9506-27 with circular geometry. Moisture ratio decreased with increasing drying temperature. The similar tendency was exhibited by the square geometry for both varieties (Figs. 4 and 5). With the variance analysis to 95 % of dependability (Table 1), it is confirmed that the temperature affects in a notable from, the drying time, being corroborated this way the coherence that is reflected among the statistical analysis and in drying rate curve; while variables as geometry, variety and the existent interactions among the variety, geometry, and temperature are not influential in the behavior of the drying time.
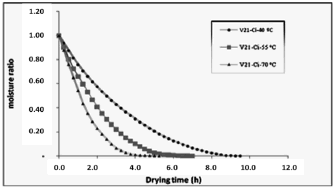
Figure 2. Effect of temperature on D. alata during air-drying, for variety 9506-21 circular geometry
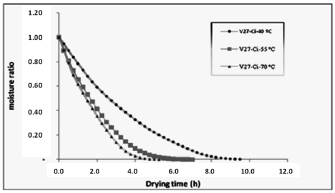
Figure 3. Effect of temperature on D. alata during air-drying, for variety 9506-27 circular geometry
Table 1. Analysis of variance (ANOVA) for drying time
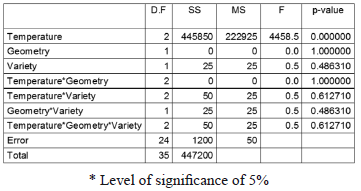
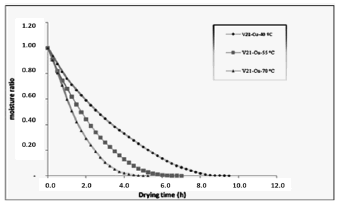
Figure 4. Effect of temperature on D. alata during air-drying, for variety 9506-21 square geometry
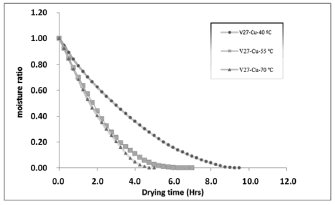
Figure 5. Effect of temperature on D. alata during air-drying, for variety 9506-27 square geometry
This behavior could be due to that the varieties used in the drying process belong to the same gender, they were cultivated under the same environmental conditions, floor type, nutritious and time of crop, presenting structure therefore interns similar; and as for the geometry the superficial area of each sample was same for all the treatments, prevailing this variable with regard to the form. Generally, in one hand, higher drying temperatures resulted in steeper curves and shorter drying times. The time required to reduce the moisture ratio to any given level was dependent on the drying temperature. According to Doymaz (2005), the effect of drying air temperature was most dramatic with moisture ratio, moisture ratio decreased rapidly with increased drying air temperature. These results were also obtained for Park, Vohnkova & Brod (2002); Maldonado & Pacheco (2003); Vega & Fito (2005); Simal, Dey & Rossell, (1997); Doymaz (2005); Mohapatra & Rao (2005); Vega & Lemus (2006) and Ocampo (2006), working with other species; vegetables and cereals. On the other hand, just the first three hours of drying from the total ten ones to obtain the constant humidity (Figures 2-5), free humidity decreased lineally with the time, drying occurred predominantly in the falling rate period. This showed that diffusion is the dominant physical mechanism governing moisture movements in the yam samples. Similar results were reported for greenbean (Rosello et al., 1997), okra (Doymaz, 2004a; Gogus & Maskan, 1999), red chilli (Gupta, et al., 2002), Carrot (Doymaz, 2004b; Prabhanjan, Ramaswamy & Raghavan, 1995) and eggplant (Ertekin & Yaldiz, 2004).
3.2 Modelling of drying kinetics curves
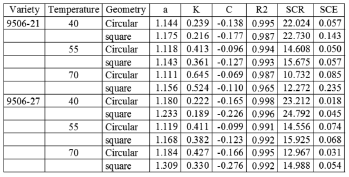
The experimental data of drying were adjusted to the mathematical models Fick's, Page's, and the Logarithmic (Tables 2, 3, and 4). According to the obtained adjustments and to the evaluation of each proposed pattern and using the coefficient of determination (R2), the sum of square of the model (SCM) and the sum of square of the error (SCE), it was determined that the model that better describes the behavior of the data of D. alata during air-drying, for varieties 9506-21 and 9506-27 in geometries circular and square for the temperatures of 40, 55, and 70 ºC, it is the Logarithmic. In the Table 4 can observe as the parameter K1 their value it increases with the increment of the temperature, coinciding this result with the obtained by Ertekin & Yaldiz (2004); Correa, da Silva & Almeida (2004); Babilis & Belessiotis (2004); Vega & Fito (2005); Vega & Lemus (2006), and Falade et al. (2006) for the eggplant drying, onion, fig, red pepper, Chilean papaya and yam (varieties D. alata and D. rotundata), respectively. In the same sense, the parameters a and b don't vary significantly for the geometries and the varieties, being these results confirmed with the variance analysis (ANOVA) for these constants at a level of dependability of 95 %.
Table 2. Page's equation parameters of D. alata, for two varieties (9506-21 and 9506-21) and two geometries (circular and square)

Table 3. Fick's equation parameters of D. alata, for two varieties (9506-21 and 9506-21) and two geometries (circular and square)
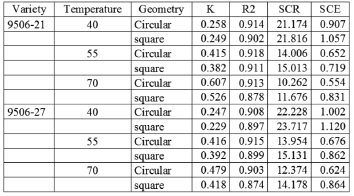
Table 4. Logarithmic equation parameters of D. alata, for two varieties (9506-21 and 9506-21) and two geometries (circular and square)
3.3 Diffusivity of yam slices
Diffusion method was used in the study of the transfer of mass of agricultural products (Vega & Fito, 2005). For the case of the D. alata the integrated equation of the second law of Fick was used (Eq. 6) for long times and plane geometry in a dimension. The effective diffusivity (Df) for each temperature it could be to adjusting the experimental data for non lineal regression.
The effective diffusivity (Df) presents a direct relation with to the temperature, and they are independent of the geometry and of the varieties (Table 5). In general, those calculated of the coefficients diffusive starting from the experimental data, they presented a good adjustment to Arrhenius equation (Table 6).
Table 5. Moisture diffusivity (m2/s) of D. alata, for two varieties (9506-21 and 9506-21) and two geometries (circular and square)
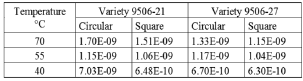
Table 6. Diffusion coefficient (D0) and activation energy (Ea) mass diffusion, during air dying, of D. alata, for two varieties (9506-21 and 9506-21) and two geometries (circular and square)
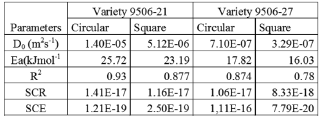
3.4. Activation energy for drying of yam.
With the values of effective diffusivity to the different temperatures, the activation energy (kJ/mol) for drying was calculated, for the two geometry and the two varieties, for non lineal regression starting from the equation of Arrhenius, with high determination coefficients (R2 = 0.870 - 0.930), indicating a good fit (Table 6). Activation energy for drying is the energy required to initiate mass diffusion from a wet food material during drying (Mittal, 1999). Activation energy for drying ranged from 23.19 to 25.72 and 16.03 to 17.82 kJ/mol for D. alata variety 9506-21 and variety 9506-27 respectively (Table 6), however, varieties and geometries showed no significant effect (p < 0.05) on activation energy for mass diffusion. Activation energy (Ea) obtained in our work is comparable with existing literatures for D. alata, 25.26 to 46.46 kJ/mol (Falades et al., 2006); carrot, 28.39 kJ/mol (Doymaz, 2004b), and potato, 20.0 kJ/mol (Bon et al., 1997). Values of the energy of activation lie within the general range of 12.7-110 kJ/mol for food materials (Zogzas, Maroulis & Marine-Kouris, 1996).
4. CONCLUSIONS
Increasing in air temperature caused a reduction in the drying time of the yams, but the variety and the geometry do not influence it.
Fick's, Page's, and logarithmic models showeds a good fit to the experimental data, nevertheless, this last is the one that better describe them, with a good coefficient of determination (below 0.96) and the sums of (deviation) squares errors were below 0.3. Fick's, Page's, and logarithmic equation parameters did not exhibit a clear trend with varieties and geometries, but the air temperature had some influence on drying constant.
The increase of air temperature and air velocity increased the effective water diffusivity values.
Activation energy to dry off is affected by the variety of the yam but not significantly (p < 0.05). Activation energy for the D. alata 9506-21 (23.19-25.72 kJ/mol) it was significantly higher than the D. alata 9506-27. (16.03-17.82 kJ/mol).
REFERENCES
[1] Akanbi, C., Gureje, P., and Adeyemi, I., Effect of heat moisture pre-treatment on physical characteristics of dehydrated yam. Journal of Food Engineering, 28(1), pp. 45-54, 1996. [ Links ]
[2] Akingbala, J., Oguntimehin, T., and Sobande, A. O., Physicochemical properties and acceptability of yam flour substituted with is flour. Plants Foods for Human Nutrition, 48(1), pp. 73-80, 1995. [ Links ]
[3] Akissoe, N., Hounhonigan, D. J., Brias, N., Vernier, P., Nagô, C. M. and Olorunda, A. O., Physical chemical and sensory evaluation of dried yam (Dioscorea rotundata) tubers flours and "amala" a flour derived product. Tropical Science, 41(1), pp. 151-155, 2001 [ Links ]
[4] AOAC. Official methods of analysis of the association of official analytical chemists (14th ed.). Washington, DC: Association of Official Analytical Chemists. 1997. [ Links ]
[5] Babalis, S. and Belessiotis, V., Influence of the drying conditions on the drying constants and moisture diffusivity during monkey-layer drying figs. Journal of Food Engineering, 65(3), pp. 449-458, 2004. [ Links ]
[6] Bon, J., Simal, S., Rosello, C. and Mullet, A., Drying characteristic of hemispherical solids. Journal of Food Engineering, 34(2), pp. 109-1220, 1997. [ Links ]
[7] Cardoso, A., and Asis, F., Comparison of mathematical models of isothermic heat of desorción in pulp of Guava. Brazil journal storage, 29(1), pp. 28-34, 2004. [ Links ]
[8] Correa, P., Da Silva, P., and Almeida, L., Estudo das propriedades físicas e de transporte na secagem de cebola (Allium cepa L.) em camada delgada. Ciência y tecnologia de los alimentos, 24(3), pp. 319-326, 2004. [ Links ]
[9] CRANK, J. The Mathematics of Diffusion (2 ed). Oxford: Claredon Press. 1975. [ Links ]
[10] DNP. 2006. National Planning Department. Colombia. Bogotá. (Available from http:www.dnp.gov.co/archivos/documentos/DDRS_Indicadores/Tab28.PDF. March 8th 2008). [ Links ]
[11] Doymaz, I., and Shovel, M., Hot-air drying characteristics of net pepper. Journal of Food of Engineering, 55(4), pp. 331-335, 2002. [ Links ]
[12] Doymaz, I., Pretreatment effect on sun drying of mulberry fruits (Morus dawn L.). Journal of Food Engineering, 65(2), pp. 205-209, 2004a. [ Links ]
[13] Doymaz, I., Convective air drying characteristics of thin-layer carrots. Journal of Food Engineering, 61(3), pp. 359-364, 2004b. [ Links ]
[14] Doymaz, I., Drying characteristics and kinetics of okra. Journal of Food Engineering, 69(3), pp. 275-279, 2005. [ Links ]
[15] Ertekin, C., Yaldiz, O., Drying of eggplant and selection of to suitable thin layer drying model. Journal of Food Engineering, 63(3), pp. 349-359, 2004. [ Links ]
[16] Falade, K., Olurin, T., Ike, E., and Aworh, O., Effect of pretreatment and temperature on air-drying of Dioscorea alata and Dioscorea rotundata slices. Journal of Food Engineering, 80(4), pp. 1002-1010, 2007. [ Links ]
[17] Gogus, F., and Maskan, M., Water adsorption and drying characteristics of okra (Hibiscus esculentus L.). Drying Technology, 17(4), pp. 883-894, 1999. [ Links ]
[18] Gupta, P., Ahmed, J., Shivhare, U.S., and Raghavan, G., Drying characteristics of red chilli. Drying Technology, 20(10), pp. 1975-1987. 2002. [ Links ]
[19] Guzman, M., and Buitrago, G., Yam: Production of Seed for Biotechnology. Bogotá: Unibiblos. 2000. [ Links ]
[20] Karatas, S., Determination of moisture diffusivity of lentil seed during drying. Drying Technology, 51(1), pp. 183-199, 1997. [ Links ]
[21] Luikov, A. V., Heat and mass transfer in capillary-porous body. Oxford, Pergamon, 1966. [ Links ]
[22] Maldonado, R., and Pacheco, T., Curvas de deshidratación del brócoli (Brassica oleraceae L var. Italica Plenk) y coliflor (Brassica oleraceae L var. Botrytis L). Revista de la Facultad de Agronomía. 20(3), 2003, pp. 306-319. [ Links ]
[23] Maskan, M., Drying, shrinkage and rehydration characteristics of kiwifruits during hot air and microwave drying. Journal of Food Engineering, 48(2), pp. 177-182, 2001. [ Links ]
[24] Mittal, G., Mass diffusivity of food products. Food Review International, 15(1), pp. 19-66, 1999. [ Links ]
[25] Mohapatra, D., and Roa, E., A thin layer drying model of parboiled wheat. Journal of food engineering, 66(4), pp. 513-518, 2005. [ Links ]
[26] Montes, E., Torres, R., Andrade, R., Perez, O., Marimon, J. and Meza, I., Models of desorption isotherms of yam (Dioscorea rotundata). Dyna, 76(154), P. 146, 2009. [ Links ]
[27] Ocampo, A., Modelo cinético del secado de la Pulpa de mango. Revista EIA, 6(1), pp. 119-128. 2006. [ Links ]
[28] Omonigbo, S., and Ikenebomeh, M., Effect of temperature on the treatment on the chemical composition of pounded white yam during storage. Food Chemistry, 71(2), pp. 215-220, 2000. [ Links ]
[29] Opara, L., Yam storage. In Agriculture processing. Handbook of agricultural engineering, IV, pp. 182-214. 1999 [ Links ]
[30] Page, G., E. Factors influencing the maximum rates of air drying shelled corn in thin layers. Indiana, [M.Sc. Thesis], Purdue University, 1949. [ Links ]
[31] Park, K., Vohnkova, Z., and Brod, F., Evaluation of drying parameters and desorption isotherms of garden mints leaves (Mentha crispa L.). Journal of Food Engineering, 51( 3), pp. 193-199, 2002. [ Links ]
[32] Prabhanjan, D., Ramaswamy, H., and Raghavan, G., Microwave-assisted convective air drying of thin layer carrots. Journal of Food Engineering, 25, pp. 283-293, 1995. [ Links ]
[33] Rosello, C., Simal, S., Sanjuán, N. and Mulet, A., Nonisotropic mass transfer model for green bean drying. Journal of Agricultural and Food Chemistry, 45, pp. 337-342, 1997. [ Links ]
[34] Ruiz, A., and Montero, I., Drying lot of industrial residuals of the olive. Alimentación equipos y tecnología, 24, pp. 122-134, 2005. [ Links ]
[35] Saravacos, G., Mass transfer properties of foods. In M. A. I fray & S. S. H. Rizvi (Eds.). Engineering properties of foods. New York: Marcel Dekker, 1995. [ Links ]
[36] Senadeera, W., Bhandari, B., Young. G., and Wijesinghe, B., Influence of shapes of selected vegetables materials on drying kinetics during fluidized bed drying. Journal of Food Engineering, 58(3), pp. 277-283, 2003. [ Links ]
[37] Simal. S., Deyá, E., Frau, M. and Rossello, C., Simple modelling of drying curves of fresh and osmotically pre-dehydrated apple cubes. Journal of Food Engineering, 33(1), pp. 139-150, 1997. [ Links ]
[38] Statistica for Windows 5.0. Computer manual program. StatSoft. Inc.. Tulsa, 1995. [ Links ]
[39] Treybal, R., Mass Transfer Operations, 3 Ed. New York: Mc Graw-Hill, 1995. [ Links ]
[40] Vega, A., and Fito. P., Modeling of the kinetics of drying of the Red pepper (capsicum annuum L. cv Lamuyo). Información tecnológica, 16(6), pp. 3-11, 2005. [ Links ]
[41] Vega, A. and Lemus, R., Modeling of the kinetics of drying of Chilean papaya (basconcellea pubescens). Información tecnológica, 17(3), pp. 23-31, 2006. [ Links ]
[42] Zogzas, N., Maroulis, Z. and Marine-Kouris, D., Moisture diffusivity dates compilation in foodstuffs. Drying Technology, 14(10), pp. 2225-2253, 1996 [ Links ]














