Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.79 no.172 Medellín Mar./Apr. 2012
INDUCED MOMENTS AND LATERAL DEFLECTIONS IN COLUMNS WITH INITIAL IMPERFECTIONS AND SEMIRIGID CONNECTIONS: I. THEORY
MOMENTOS INDUCIDOS Y DEFLEXIONES LATERALES EN COLUMNAS CON IMPERFECCIONES INICIALES Y CONEXIONES SEMIRIGIDAS: I. TEORIA
J. DARIO ARISTIZABAL-OCHOA
Ph.D. School of Mines, National University, Medellin, Colombia, jdaristi@unal.edu.co
Received for review November 11th, 2011, accepted February 9th, 2012, final version February, 14th, 2012
ABSTRACT: Closed-form expressions that can be used to evaluate induced elastic bending moments and second-order deflections in slender prismatic columns with initial geometric imperfections (i.e., initial curvature and out-of-plumbness) and semirigid connections when subjected to eccentric axial loads at both ends, are derived in a classical manner. The proposed approach is based on the classical Euler-Bernoulli theory for columns with uninhibited, partially-inhibited, and totally-inhibited sidesway. The combined effects of initial imperfections, axial load eccentricities, and semirigid connections are condensed into the proposed equations. The effects of shear and axial deformations along the member span are not included. Comparisons of the induced elastic moments, second-order deflections, and critical loads obtained using the proposed approach and those available in the technical literature for classic column cases, are presented in a companion paper. Also, sensitivity studies and several examples are presented in detail. These demonstrate the effectiveness and accuracy of the proposed closed-form equations and the importance of initial imperfections, semirigid connections, and lateral bracing on the second-order behavior and stability of beam-columns. These effects must be taken into account in the analysis and design of imperfect slender columns subjected to high axial loads, particularly when sidesway between its ends is uninhibited or partially inhibited due to possible failure by lateral collapse.
KEY WORDS: Beam-columns, bracing, buckling, columns, computer applications, deflections, design, frames, large deflections, loads, reversals of deflections, second-order analysis, stability.
RESUMEN: Se derivan de una manera clásica expresiones cerradas capaces de evaluar los momentos de flexión y deformaciones laterales elásticas de segundo-orden inducidas en columnas prismáticas esbeltas con conexiones semirrígidas y con imperfecciones iniciales geométricas (tales como curvatura y desplome iníciales) sometidas a fuerrzas axiales excéntricas en ambos extremos. El enfoque propuesto se basa en la teoría clásica de Euler-Bernoulli para columnas con deriva lateral sin inhibiciones, parcialmente inhibida, y se inhibida totalmente. Los efectos combinados de las imperfecciones iniciales, las excentricidades de la carga axial y las conexiones semirrígidas son condensados en las ecuaciones propuestas. Los efectos de las deformaciones axiales y por cortante a lo largo de los miembros no están incluidos. En una publicación adjunta se presentan comparaciones de los momentos inducidos y las deformaciones de segundo-orden y las cargas críticas obtenidas utilizando el método propuesto con los que están disponibles en la literatura técnica para los casos clásicos. También se presenta en detalle estudios de sensibilidad y varios ejemplos que demuestran la eficacia y la precisión del método propuesto y sus ecuaciones cerradas, como también de la importancia de las imperfecciones iniciales, las conexiones semirrígidas y arriostramiento lateral sobre el comportamiento de segundo- orden y la estabilidad de vigas-columnas. Estos efectos deben tenerse en cuenta en el análisis y diseño de columnas esbeltas imperfectas sometidas a altas cargas axiales, sobre todo cuando la deriva lateral entre sus extremos es desinhibida o parcialmente inhibida debido a la posibilidad de colapso lateral.
PALABRAS CLAVE: Vigas-columnas, arriostramiento, pandeo, columnas, aplicaciones informáticas, deflexiones, diseño, marcos, grandes deflexiones, cargas, reversión de deflexiones, análisis de segundo-orden, estabilidad.
1. INTRODUCTION
The effects of initial imperfections on the elastic response of slender columns subjected to axial loads are of great importance within both structural engineering and structural mechanics. These effects, particularly those related to their stability and lateral deflections, have been studied by a large number of researchers and discussed in the technical literature [1-4]. However, due to space limitations, some research studies carried out in the last 25 years are cited below.
Razzaq and Calash [5] studied the effects of biaxial semirigid connections on the inelastic response of hollow rectangular steel nonsway columns with biaxial crookedness and residual stresses. They found that residual stresses were less detrimental to column strength than initial crookedness and that the column maximum axial load capacity is always associated with a severe or complete plastification at and around its midspan. Britvec and Davister [6] studied the post-buckling equilibrium paths of complex, elastic, hyperstatic, pin-jointed lattices composed of slender members using a simplified matrix formulation including the effects of initial geometrical imperfections on the post-buckling paths. More recently, Davister [7] developed a numerical method to determine the most unstable post-buckling mode capable of developing at the ultimate critical state of complex pin-jointed structures. Chan and Zhou [8] presented a method that included the effects of initial imperfections in the column element stiffness matrix. More recently, Chan, Huang and Fang [9] developed a finite element procedure for large-deflection and the inelastic analysis of imperfect steel frames with a semirigid base with various modes of initial imperfection. Kim and Chen [10,11] presented procedures for 2D braced and unbraced steel frame analysis and design including gradual yielding associated with flexure, residual stresses, second-order effects, and geometric imperfections.
Smith-Pardo and Aristizabal-Ochoa [12,13] developed expressions and design aids for the transverse and longitudinal deflections of an axially-restrained beam-column under plane loads including the second-order effects and initial imperfections. Aristizabal-Ochoa [14] developed a closed-form expression for the geometrical-nonlinear axial stiffness of a beam column including not only the combined effects of biaxial bending end moments but those of transverse forces, initial imperfections (both camber and sweep), and out-of-plumbness.
Xu and Wang [15] carried out parametric studies on the effects of initial imperfections on the lateral stability of unbraced plane frames. They found that: 1) the increase of effective length factor increases either one of the initial geometrical imperfection almost linearly; 2) out-of-straightness has a greater detrimental effect than that of the out-of-plumbness; and 3) given the same value of the initial geometric imperfection, the influence of out-of-straightness on the column effective length factor is almost double that of the out-of-plumbness. They concluded that "This finding is consistent with current practice in which the tolerance for the out-of-straightness and the out-of-plumbness are L/1000 and L/500, respectively." More recently, Hellesland [16] studied the mechanics of column interaction in single curvature regions in multistory frames with the sidesway uninhibited and proposed an approximate story magnifier approach.
In spite of significant advances in the knowledge regarding the behavior, strength, and design of columns, closed-form expressions that evaluate the induced elastic bending moments and second-order deflections in slender prismatic columns with initial geometric imperfections (i.e., initial curvature, out-of-plumbness, and axial load eccentricities), and semirigid connections such as the applied axial load increases are not available in the technical literature. Formulas that can be used in the analysis of columns that exceed the out-of-straightness and out-of-plumbness tolerated by construction codes are nonexistent. The main objective of this paper is precisely that, to present closed-form expressions for Euler-Bernoulli columns with uninhibited, partially-inhibited, and totally-inhibited sidesway that can be used in their analysis. The effects of shear and axial deformations along the member span are not included. Comparisons of the induced elastic moments, second-order deflections, and critical loads obtained using the proposed approach and those available in the technical literature for classic column cases are presented in a companion paper.
2. STRUCTURAL MODEL
2.1. Assumptions
Consider the slender 2D prismatic column shown in Fig. 1. The element is made up of the column AB itself, the lumped bending connections ka and kb, and the lateral bracing at the top end B, of stiffness SD. It is assumed that: 1) the column AB is made of a linear elastic material with elastic modulus E and height h; 2) the centroidal axis of the column is not perfectly straight, but has an initial imperfection defined by a symmetric parabola at about the midspan of the column: 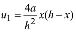 or by a series of sinusoidal waves
or by a series of sinusoidal waves 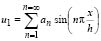
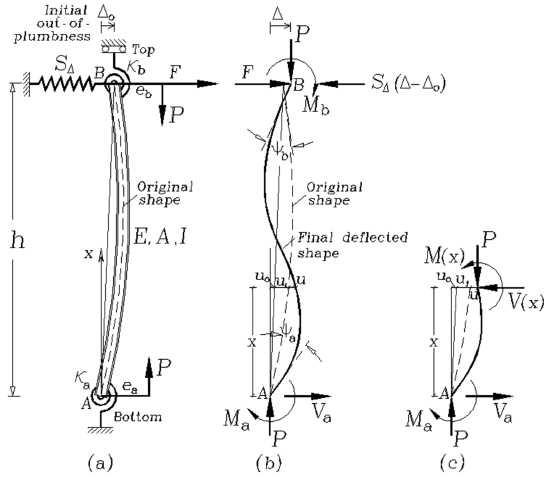
Figure 1. Model of a imperfect column with sidesway partially inhibited and rotational end restraints: (a) structural model with eccentric axial loads applied at the column extremes; b) end moments, forces, rotations and deflections; and c) column segment including lateral deflections, bending moments, shear and axial forces
and its out-of-plumb is defined by the lateral sway Do. 3) The column is loaded at both ends with a vertical load P with eccentricities ea and eb and a horizontal force at the top end B. 4) The column is perfectly prismatic with a symmetric cross-section with gross area A, principal moment of inertia I in the plane of bending. 5) Deformations and strains are small so that the principle of superposition can be applied.
The lumped bending connections have stiffness ka and kb (whose units are in force-distance/radian), respectively. The units of lateral bracing SD are in force/distance. The ratios Ra = ka/(EI/h) and Rb = kb/(EI/h) are denoted as the stiffness indices of the flexural connections. These indices vary from zero (i.e., Ra = Rb = 0) for simple connections (i.e., perfectly pinned) to infinity (i.e., Ra = Rb = ¥) for fully restrained connections (i.e., perfectly rigid). For the convenience of the reader, the following two parameters are introduced:
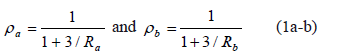
ra and rb are called the fixity factors. For perfectly hinged connections, both the fixity factor r and the rigidity index R are zero; but for perfectly rigid connections, the fixity factor is 1 and the rigidity index is infinity. Since the fixity factor varies from 0 to 1 for elastic connections (while the rigidity index R varies from 0 to ¥), it is more convenient to use in the analysis of structures with semirigid connections.
3. SECOND-ORDER ANALYSIS
The second-order lateral deflection (u) and corresponding slope (du/dx) along the height of the column caused by the axial load P (assuming ea = eb = D = Do = 0) with initial curvature given by a parabola or by a series of sinusoidal waves, are derived in Sections 6.1 and 6.2 of the Appendix, respectively. In Section 6.3 of the Appendix, a complete second-order analysis is carried out for the partially-braced column (Fig. 1a) with semirigid connections and initial out-of-plumbness Do subjected to F and P, with eccentricities ea and eb at ends A and B, respectively.
4. COLUMN TYPES AND PROPOSED CLOSED-FORM EQUATIONS
4.1. Columns with sidesway inhibited (i.e., D - Do = 0)
The end moments in columns with lateral sway between their ends totally inhibited (Fig. 2a) can be obtained from Eqs. (27a-b) by making D - Do = 0 as follows:
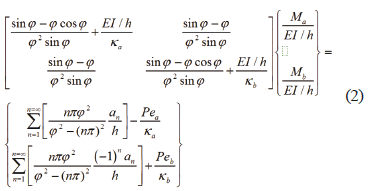
Therefore, the proposed closed-form expressions for the end moments Ma and Mb become
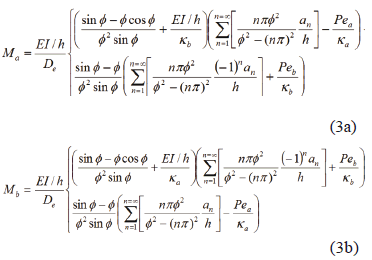
Expressions (3a)-(3b), in terms of the fixity factors, become

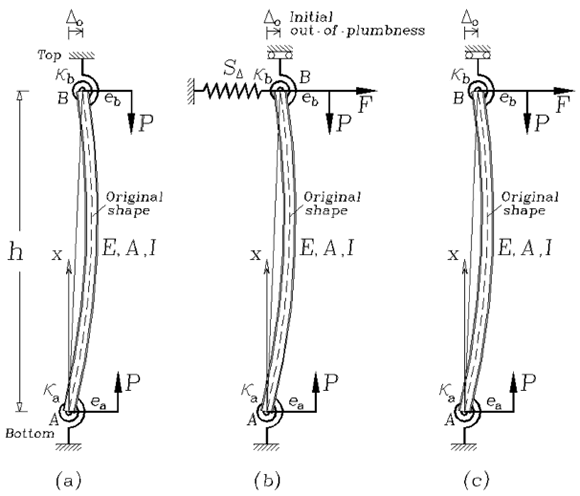
Figure 2. Models of an imperfect column with rotational end restraints and with sidesway: (a) totally inhibited, (b) partially inhibited, and (c) uninhibited
Notice that expression (5a), when made equal to zero, becomes the characteristic equation from which the critical buckling loads of columns with sidesway inhibited (Fig. 1a) can be calculated, and it is identical to the one derived by Timoshenko and Gere Eq. (2-21) p. 60 in ref. [1].
It is important to emphasize that the induced moments, lateral deflections, and critical loads in columns with sidesway inhibited (i.e., D - Do = 0) are not affected by the initial out-of-plumbness Do as indicated by Eqs. (2-5). This is true as long as Do/h is small, as stated in the previous paragraph.
4.2. Columns with sidesway partially inhibited
For columns in which the lateral sway between the two ends is partially inhibited (i.e., D - Do1 0) by spring SD (Fig. 2b), the end moments and lateral sway can be obtained from Eq. (29a) as follows:
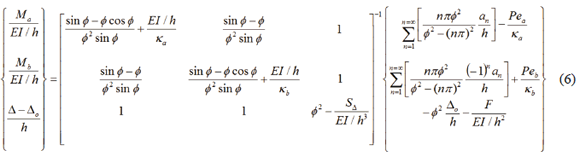
The determinant of the square matrix 3´3 on the right hand of Eq. (6) is as follows:
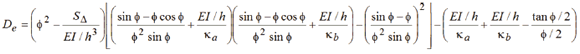
which in terms of the fixity factors, becomes
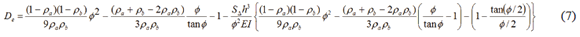
Notice that when expression (7) is made equal to zero, it becomes the characteristic equation from which the critical buckling loads of columns with sidesway partially inhibited (Fig. 1b) can be calculated.
A partially-braced column is one which critical load Pcr lies between that of the column with sidesway uninhibited ("unbraced") and that of the column with sidesway totally inhibited ("braced"). Notice also that the proper evaluation of SD is vital to the stability analysis of framed structures. In general, there are three sources of SD: 1) those provided by other columns which are part of the same story level from which column AB is located; 2) those which are from diagonal bracing or shear walls within the same story level of the frame; and 3) those which are from the external bracing provided by other structures or structural elements connected to the column's top and bottom levels. For instance, the lateral stiffness provided by a perfectly straight and vertical single column under a concentric compressive axial load N derived by Aristizabal-Ochoa [17, 18, 19] is as follows:
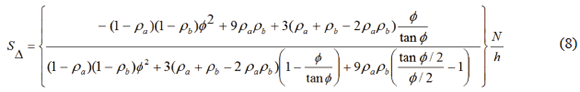
The spring SD provided by a single diagonal bracing of cross-sectional area Ab, horizontal length L, and height h is:
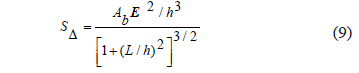
(9) is derived by Salmon and Johnston [20].
4.3. Columns with sidesway uninhibited
For columns in which the lateral sway between the two ends is uninhibited; i.e., D - Do 1 0 and SD = 0, (Fig. 2c); the end moments and lateral sway can be obtained by making SD = 0 in Eq. (6) with expression (7) reduced to
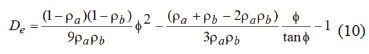
As in the previous two cases when expression (10) is made equal to zero, it becomes the characteristic equation from which the critical buckling loads of columns with sidesway uninhibited (Fig. 1c) can be calculated. Notice that the induced moments and lateral deflections in columns with sidesway uninhibited or partially inhibited (i.e., D -Do1 0) are affected by the initial out-of-plumbness Do, as indicated by Eq. (6).
For ease and clarity, the closed-form expressions for the end moments Ma and Mb, lateral sway (D - Do), and the characteristic equation, as well as the expressions for the bending moment M(x) and transverse deflection u(x), are listed in Table 1 for the three column cases just described. For columns with initial parabolic imperfections, the terms 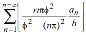 and
and 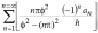 in all equations listed above and in Table 1 must be substituted for
in all equations listed above and in Table 1 must be substituted for 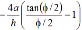 and
and 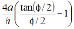 , respectively.
, respectively.
5. SUMMARY AND CONCLUSIONS
Closed-form expressions that can be used to evaluate the induced bending moments and second-order lateral deflections of imperfect slender prismatic columns when subjected to eccentric axial loads at both ends are derived in a classical manner. The proposed approach is based on the classical Euler-Bernoulli theory for columns with uninhibited, partially-inhibited, and totally-inhibited sidesway. The effects of initial imperfections (initial curvature, out-of-plumbness, and axial load eccentricities at both ends) and semirigid connections are condensed into the proposed equations. The concept of the end-fixity factor is used to characterize the rotational restraints at both ends of the column. The effects of shear and axial deformations along the member span are not included in the analysis.
The proposed closed-form solutions enable the analyst to explicitly evaluate the effects of initial curvature, out-of-plumbness, and axial load eccentricities on the induced bending moments, second-order deflections of slender prismatic columns with semirigid connections at both ends and with sidesway uninhibited, partially inhibited, and totally inhibited as the axial load is applied.
It is a common practice in the design of columns that the effects of initial geometric imperfections are taken into account for specific values according to accepted fabrication and erection tolerances. However, to investigate these effects when the magnitudes and shape of the imperfections are different from those adopted by the construction codes becomes a cumbersome task. Therefore, the proposed closed-form expressions might become a practical tool of great interest to structural designers and researchers to further study these effects in accordance with design practices and code specifications.
6. APPENDIX: SECOND-ORDER ANALYSIS
6.1. Second-order deflection and slope assuming an initial imperfection of parabolic shape:
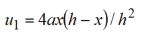
Knowing that: 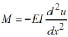 , then
, then
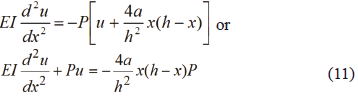
Applying the boundary conditions: 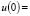
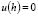 , then the solution to Eq. (23) is given by
, then the solution to Eq. (23) is given by
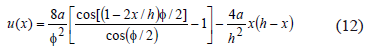
Therefore,
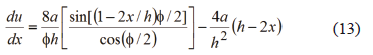
where 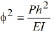 ; and a = initial camber at midspan.
; and a = initial camber at midspan.
6.2. Second-order deflection and slope assuming an initial imperfection as a series of sinusoidal waves
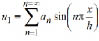
Knowing that 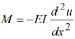 , then
, then
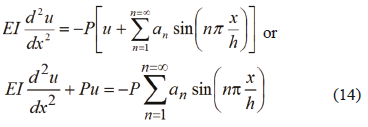
Applying the boundary conditions 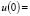
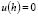 , then the solution to Eq. (26) is
, then the solution to Eq. (26) is
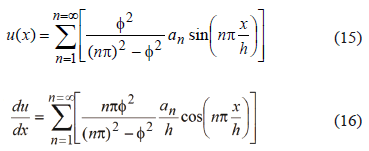
Where: an = the peak value of the initial camber corresponding to the n-wave.
6.3. Complete second-order analysis
Applying moment and lateral equilibrium on the beam-column shown by Fig. 1b,
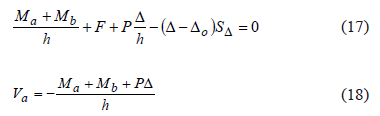
Applying equilibrium on the column at a distance x from extreme A (Fig. 1c),
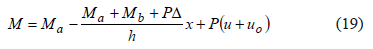
Knowing that 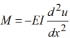 and uo= Dox/h then
and uo= Dox/h then
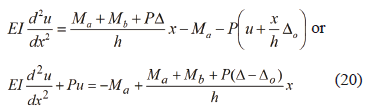
The solution to Eq. (20) is given by
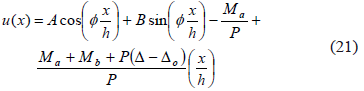
Applying the following boundary conditions: 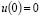 and
and 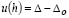 , constants A and B become:
, constants A and B become:
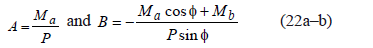
Therefore,
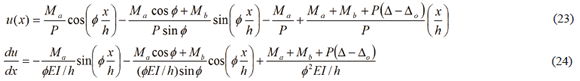
Applying superposition by adding expressions (15) and (23), as well as (16) and (24), the expressions (25) and (26) for total deflection and rotation become:
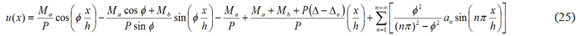
Table 1. Closed-form expressions for moments and deflections, and characteristic equationsColumns with sidesway inhibited (i.e., D - Do = 0)
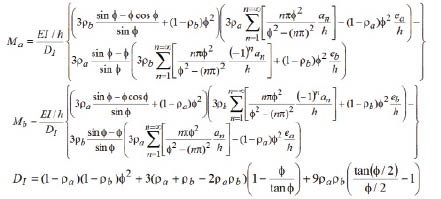
Characteristic Equation: 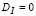 Columns with sidesway partially inhibited (SD1 0) and uninhibited (SD = 0)
Columns with sidesway partially inhibited (SD1 0) and uninhibited (SD = 0)

Characteristic equation: 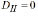
For all cases above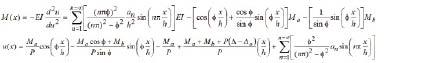
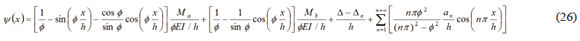
Knowing that from rotational compatibility and equilibrium at ends A and B of the beam-column of Fig. 1(b), 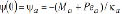 and
and 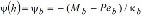 , the following expressions can be obtained:
, the following expressions can be obtained:
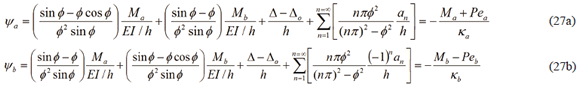
Where: 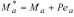 and
and 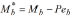 are the end bending moments induced by the connections ka and kb of the column of Fig. 1a, respectively.
are the end bending moments induced by the connections ka and kb of the column of Fig. 1a, respectively.
Equation (17) can be expressed as follows:
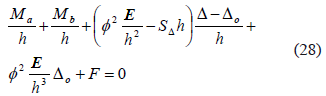
Now, expressing (27a-b) and (28) in matrix form,
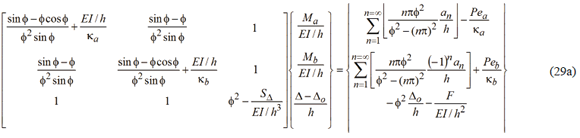
Equation (29a) represents the second-order results of the beam-column of Fig. 1a with semirigid connections at both ends and laterally braced at A from which the end moments Ma and Mb and lateral sway D - Do can be determined at given axial load (P) and its eccentricities (ea and eb), the lateral force (F), and initial set of imperfections (Do and an). Likewise, Eq. (29b) which follows, represents the same results but using the parabolic distribution explained above in Section 5.1 with a being the initial camber at mid-span.
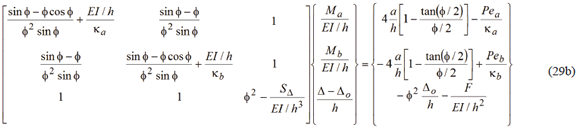
Notice that once the end moments Ma and Mb are calculated from Eqs. (29a-b), the end moments induced by the connections 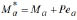 and
and 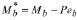 for the column of Fig. 1a, can be evaluated directly. Also, the second-order deflections and slopes can be calculated from Eqs. (25) and (26), respectively; and finally, the bending moment along the member from Eq. (30).
for the column of Fig. 1a, can be evaluated directly. Also, the second-order deflections and slopes can be calculated from Eqs. (25) and (26), respectively; and finally, the bending moment along the member from Eq. (30).
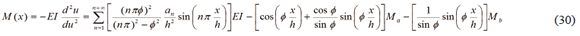
It must be emphasized that for the proposed method and corresponding Eqs. (17)-(30) to be valid, the lateral deflections u must relatively small and the ratio (D - Do)/h must also be a small angle, as assumed in Eqs. (39a-b).
ACKNOWLEDGMENTS
The research presented in this paper was carried out at the National University of Colombia, School of Mines at Medellin. The author wants to express his appreciation to DIME for the financial support.
REFERENCES
[1] Timoshenko, S. P. and Gere, J. M., Theory of Elastic Stability, 2nd Ed., McGraw-Hill Book Inc., New York, N.Y, 1961. [ Links ]
[2] Chen, W. F. and Lui, E. M., Structural Stability: Theory and Implementation, Prentice Hall, Chapter 2, 1987. [ Links ]
[3] Chajes, A., Principles of Structural Stability Theory, Prentice Hall, pp. 28-35, 1993. [ Links ]
[4] Galambos, T. V., Guide to stability design criteria for metal structures, Wiley, 5th Edition, Chapters 2 and 3, 911 P. 1995. [ Links ]
[5] Razzaq, Z. and Calash, A. Y., Imperfect Columns with Biaxial Partial Restraints, J. of Structural Engineering, Vol. 111(4), pp. 758-77, 1985. [ Links ]
[6] Britvec, S. J. and Davister, M. D., Post-Buckling Equilibrium of Hyperstatic Lattices, J. of Engineering Mechanics, Vol. 111(3), pp. 287-310, 1985. [ Links ]
[7] Davister, M. D., The Most Degrading Postbuckling Mode of Pin-Jointed Structures, J. of Engineering Mechanics, Vol. 132(7), pp. 775-779, 2006. [ Links ]
[8] Chan, S. L. and Zhou, Z. H., Second-Order Elastic Analysis of Frames Using Single Imperfect Element per Member, J. of Structural Engineering, Vol. 121(6), pp. 939-945, 1995. [ Links ]
[9] Chan, S. L., Huang, H. Y. and Fang, L. X., Advanced Analysis of Imperfect Portal Frames with Semirigid Base Connections, J. of Engineering Mechanics, Vol. 131(6), pp. 633-640, 2005. [ Links ]
[10] Kim, S-E. and Chen, W-F., Practical Advanced Analysis for Unbraced Steel Frame Design, J. of Structural Engineering, Vol. 122(11), pp. 1259-1265, 1996. [ Links ]
[11] Kim, S-E. and Chen, W-F., Practical Advanced Analysis for Braced Steel Frame Design, J. of Structural Engineering, Vol. 11 (122), pp. 1266-1274, 1996. [ Links ]
[12] Smith, P., Paul, J. and Aristizabal, J. D., Buckling Reversals of Axially Restrained Imperfect Beam-Column, J. of Engineering Mechanics, Vol. 125(4), pp. 401-409, 1999. [ Links ]
[13] Smith, P., Paul, J. and Aristizabal, J. D., Second-order axial force and midspan deflection in a simple supported beam axially restrained, Engineering Structures, Vol. 30(2), pp. 561-569, 2008. [ Links ]
[14] Aristizabal, J. D., Second-Order Axial Deflections of an Imperfect Beam-Column, J. of Engineering Mechanics, Vol. 126(11), pp.1201-1208, 2000. [ Links ]
[15] Xu, L. and Wang, X.H., Storey-based column effective length factors with accounting for initial geometric imperfections, Engineering Structures, Vol. 30(12), pp. 3434-3444, 2008. [ Links ]
[16] Hellesland, J., Second order approximate analysis of unbraced multistorey frames with single curvature regions, Engineering Structures, Vol. 31(8), pp. 1734-1744, 2009. [ Links ]
[17] Aristizabal, J. D., K-Factor for Columns in any Type of Construction: Nonparadoxical Approach, ASCE J. of Structural Engineering, Vol. 120(4), pp.1272-1290, 1994. [ Links ]
[18] Aristizabal, J. D., Matrices de Rigidez y de Carga de pimer and Segundo orden de una Viga-columna Ortotrópica con conexiones Semirígidas (I-Teoria), Revista DYNA, 77(164), pp. 130-140, 2010. [ Links ]
[19] Aristizabal, J. D., Matrices de Rigidez y de Carga de primer and Segundo orden de una Viga-columna Ortotrópica con conexiones Semirígidas: I) Ejemplos, Revista DYNA, 77(164), pp. 131-151, 2010. [ Links ]
[20] Salmon, C. G. and Johnson, J.E., Steel Structures: Design and Behavior, 4th Ed., HarperCollins College Publishers (Chapter 14), 1996. [ Links ]














