STRAIGHT-LINE CONVENTIONAL TRANSIENT RATE ANALYSIS FOR LONG HOMOGENEOUS AND HETEROGENEOUS RESERVOIRS

ANALISIS CONVENCIONAL PARA TRANSIENTES DE CAUDAL EN YACIMIENTOS HOMOGENEOS Y HETEROGENEOS ALARGADOS

 

FREDDY HUMBERTO ESCOBAR
Ph.D. Programa de Ingeniería de Petróleos, Universidad Surcolombiana, Professor, fescobar@usco.edu.co

MARGARITA MARIA ROJAS RODDRIGUEZ
B.Sc. Global Petroleum Service, Universidad Surcolombiana, Junior Engineer, mararita456@hotmail.com

JOSE HUMBERTO CANTILLO SILVA
M.Sc. Instituto Colombiano del Petróleo, Researcher, jose.cantillo@ecopetrol.com.co

 

Received for review July 30^th, 2010, accepted February 7^th, 2012, final version February, 9^th, 2012

 

---

ABSTRACT: A linear flow regime is a very important flow regime presented in fractured wells, horizontal wells and long reservoirs. Either pressure-transient analysis or rate-transient analysis may be affected by a linear flow regime. In the case the case of production rate most of the analysis is conducted by decline-curve fitting and little attention has been given to rate-transient analysis. This paper presents the governing equations used for rate-transient analysis in elongated systems and provides examples using the conventional analysis. The methodology allows for the estimation of reservoir permeability, reservoir width and geometrical skin factors. If the test is long enough, reservoir drainage area and well position inside the reservoir can also be determined. The methodology was successfully verified by its application to synthetic cases.

KEY WORDS: Linear flow, parabolic flow, reservoir width, well-flowing pressure

RESUMEN: El flujo lineal es un régimen de flujo muy importante que se presenta en pozos fracturados, horizontales y yacimientos alargados. Tanto el análisis de pruebas de presión como de transitorio de caudal podrán verse afectados por la presencia del flujo lineal. Para el caso de producción a caudal variable, la mayor parte del análisis se realiza mediante ajuste de curvas de declinación y poca atención ha recibido el análisis transitorio de caudal. Este artículo presenta las ecuaciones gobernantes usadas para análisis transitorio de caudal en sistemas alargados y proporciona ejemplos mediante el método convencional. La metodología permite la estimación de la permeabilidad, el ancho del yacimiento y los factores de daño geométricos. Si la prueba es lo suficientemente larga se puede estimar el área de drenaje del yacimiento y la posición del pozo dentro del mismo. La metodología se verificó satisfactoriamente mediante su aplicación a pruebas sintéticas.

PALABRAS CLAVE: Flujo lineal, flujo parabólico, ancho del yacimiento, presión de fondo fluyente

---

 

1. INTRODUCTION

Formation linear flow in vertical wells can be due to geological events (meandering), faulting or sand lens. Recently, [4] introduced the application of the TDS technique for characterization of long and homogeneous reservoirs, presenting new equations for the estimation of reservoir area, reservoir width and geometrical skin factors. They classified the linear flow regime into two categories: (a) dual-linear, when the flow takes along both sides of the well throughout the elongated reservoir part, and (b) single-linear, when the flow comes from one side of the reservoir. [2] introduced a new flow regime exhibiting a negative half slope on the pressure derivative curve once dual-linear flow has ended. [3] studied the impact of the geometric skin factors on elongated systems. Characterization of pressure tests in elongated systems using the conventional method was also presented by [4]. [5] presented a summary of the advances in characterization of long and homogenous reservoirs using transient pressure analysis. [6] were the first in applying rate-transient analysis to elongated systems. However, pressure and pressure derivative cases of naturally-fractured reservoir were later analyzed by [7].

 

2. MATHEMATICAL DEVELOPMENT

Define the following dimensionless quantities:

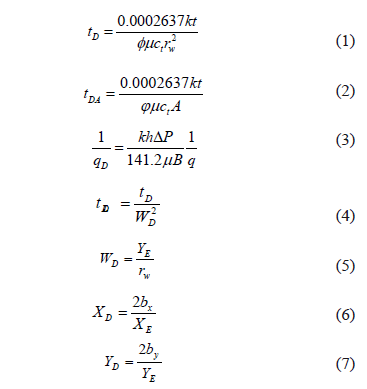
Different simulation runs were generated using the superposition principle for elongated systems with the lateral boundaries open or closed to flow. Regression analysis was applied to the reciprocal derivative curve to develop the governing equations, and then the governing reciprocal rate equation was obtained by the integration of the derivative.

2.1. Linear flow regime, homogeneous reservoirs
Linear flow is observed when the lateral boundaries of the reservoir are closed to flow and the well is off-centered inside the reservoir. The governing equation for this behavior is

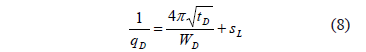
where S_L is the geometrical skin factor due to the convergence from dual-linear to linear flow. Then, by replacing the dimensionless quantities in Eq. 8, it becomes

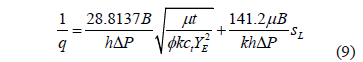
which implies that a Cartesian plot of 1/q vs. t ^0.5 will produce a straight line which slope m_LF and intercept b_LF allow to obtain

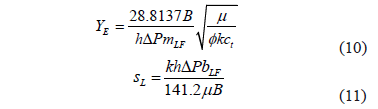
2.2. Dual-linear flow regime, homogeneous reservoir
Once the radial flow regime vanishes, two linear flows occur simultaneously opposite to each other inside the reservoir. The governing equation for this case is

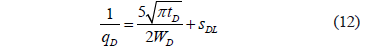
The dimensional form of Eq. 12 is

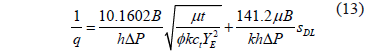
which also indicates that a Cartesian plot of 1/q vs. t ^0.5 will produce a straight line which slope m_DLF and intercept b_DLF allow to obtain

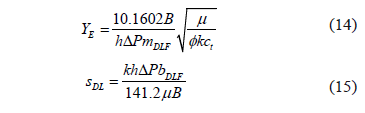
2.3. Parabolic flow regime, homogeneous reservoirs
This flow is the result of the simultaneous action of a near open boundary and a flow along the reservoir in the opposite direction. For further explanation the reader is referred to [2]. The dimensionless reciprocal rate governing the equation is given by

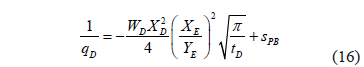
After plugging in the dimensionless equations. it will yield

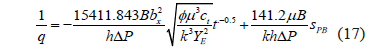
Therefore, a Cartesian plot of 1/q vs. 1/t ^0.5 will yield a straight line which slope m_PBF and intercept b_PBF allow to determine

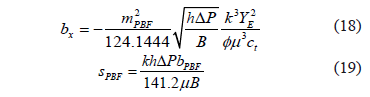
2.4. Dual-linear flow regime, heterogeneous reservoirs
For this case the governing dimensionless reciprocal rate and dimensional reciprocal rate equations are

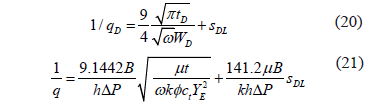
which also indicates that a Cartesian plot of 1/q vs. t ^0.5 will produce a straight line which slope m_DLF and intercept b_DLF allow to obtain

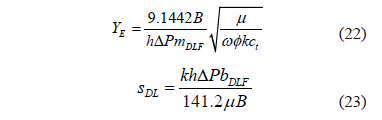
2.5. Linear flow regime, heterogeneous reservoirs
Two cases are considered. The first one takes into account that the linear flow regime shows up once the transition period of the naturally-fractured reservoir has vanished. Therefore, the governing dimensionless and dimensional equations are

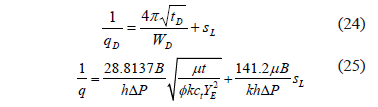
As for the former cases, Eq. 24 implies that a Cartesian plot of 1/q vs. t ^0.5 will yield a straight line which slope m_LF and intercept b_LF allow to obtain

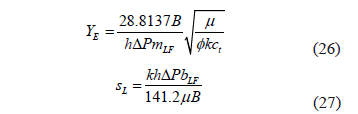
In the second case, the linear flow regime takes place before the heterogeneous transition is seen. Again, the governing equations are

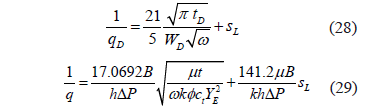
where w is the dimensionless storativity coefficient of a naturally fractured reservoir introduced by [8]. As before, a Cartesian plot of 1/q vs. t ^0.5 will produce a straight line which slope m_LF and intercept b_LF allow to obtain

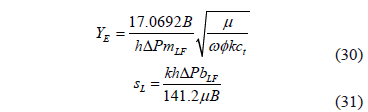
In elongated heterogeneous systems the mass transference between matrix and fractures may take place after the radial flow regime when the interporosity flow parameter l is normally lower than 1x10^-7. Then either the dual-linear or the linear flow regime may be interrupted by the transition period of the naturally-fractured system. However, in any case, dual-linear flow is normally seen after the radial flow regime. Notice that l was also introduced by [8].

Figure 1 shows a semilog plot of the reciprocal dimensionless rate times the square root of the interporosity flow parameter l as a function of the dimensionless time for different l and w values. As expected, a linear trend is observed during the radial flow regime. Then, dual-linear flow appears followed by the late pseudosteady-state period in which all the lines for the same value of l coincide. Based on that fact, a semilog plot of the reciprocal dimensionless rate vs. dimensionless time (Fig. 2) was built for different values of the dimensionless storativity parameter. From Fig. 2, a correlation between w with the intercept at time of 1 hr is given as

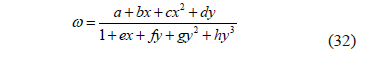
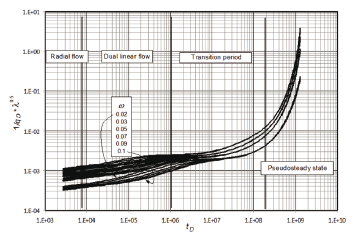
Figure 1. Semilog plot of the dimensionless reciprocal rate times the square root of the interporosity flow parameter versus the dimensionless time for different l and w values

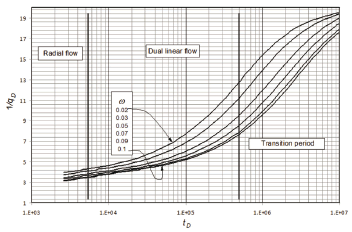
Figure 2. Semilog plot of the dimensionless reciprocal rate versus the dimensionless time for different values of w and l = 1x10^-8

for homogeneous reservoirs

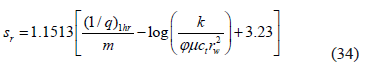
for heterogeneous reservoirs

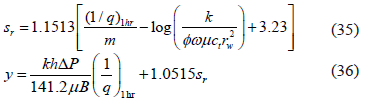
Eq. 35 is applied to -4 ≤ S_r ≤ 4 and 0.01 ≤ w ≤ 0.1. Also, for the semilog plot, the permeability is estimated from

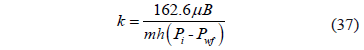
As shown in Fig. 3, the intercept on the semilog plot is a function of the mechanical skin factor sr, as shown by the excellent correlation provided in Fig. 4.

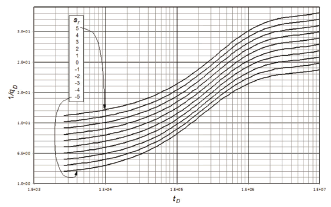
Figure 3. Semilog plot of the dimensionless reciprocal rate as a function of the dimensionless for w = 0.01, l = 1 x 10^-8 and different mechanical skin factors

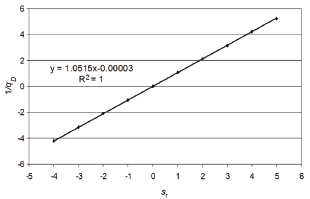
Figure 4. Relationship of the dimensionless reciprocal rate versus the mechanical skin factor for w = 0.01 and l = 1x10^-8

In this study, the equation provided by [9] is used to estimate the interporosity flow parameter

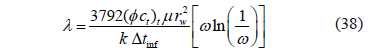
where D_tinf is the inflection point at which the minimum (trough) of the reciprocal rate derivative takes place during the transition period of the heterogeneous system. As a recommendation, the derivative plot should be used for reading that value.

 

3. EXAMPLES

The information data for all the examples is reported in Table 1.

Table 1. Input data for the examples

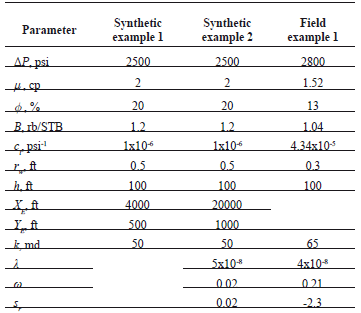
3.1. Synthetic example 1, homogeneous case
A production test for a rectangular-shaped reservoir was simulated with the information provided in Table 1. It is requested to estimate the reservoir width and dual-linear skin factor.

Solution. Figure 5 displays a plot of the reciprocal flow rate against time. From this plot, the following information was read:

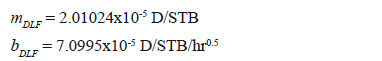
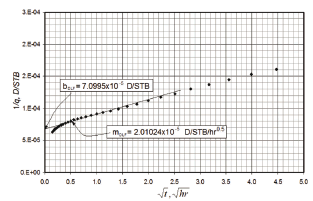
Figure 5. Cartesian plot of the reciprocal rate versus the square root of time for example 1

The reservoir width is found by means of Eq. 14 using the slope of the dual-linear flow regime

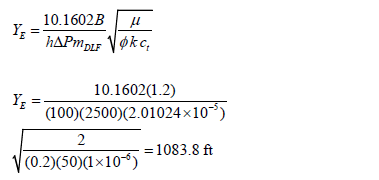
The geometrical skin factor was calculated with Eq. 15,

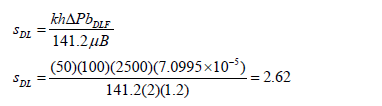
3.2. Synthetic example 2, heterogeneous reservoir
A simulated test was run with information given in Table 1. From the semilog plot, Fig. 6, a value of the slope and intercept of 3.1x10^-5 D/STB/cycle and 0.0002 D/STB, respectively, were read and the mechanical skin factor was estimated from Eq. 34

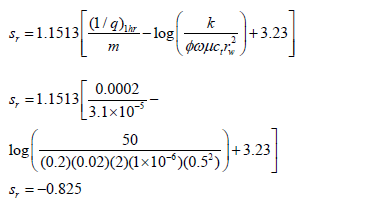
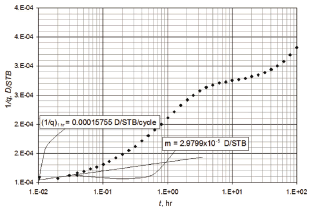
Figure 6. Semilog plot of reciprocal rate versus time for example 2

Parameters x and y from Eqs. 32 and 35 are, respectively,

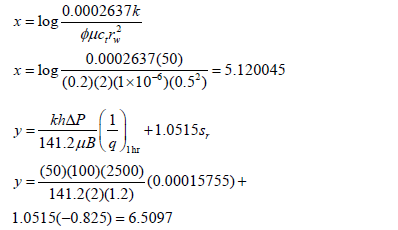
Application of Eq. 31 leads one to find

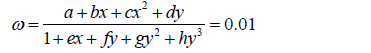
A Cartesian plot of the reciprocal rate versus the square root of time is given in Fig. 7. From this plot a slope of m_DLF = 0.000128792 D/STB/hr0.5 and an intercept of b_DLF = 9.03618x10^-5 D/STB were read, which are then used to estimate reservoir width and the dual-linear skin factor with Eqs. 21 and 22, respectively.

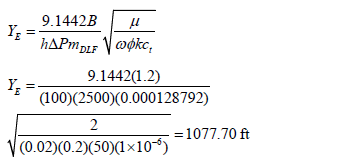
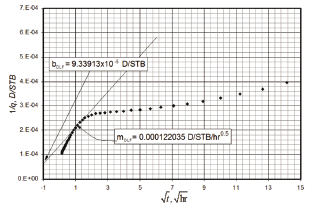
Figure 7. Cartesian plot of the reciprocal rate versus the square root of time for example 2

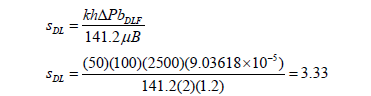
Finally, the interporosity flow parameter is estimated with Eq. 37 using a value of D_tinf = 10.047 hr, obtained from the reciprocal derivative plot, not shown here.

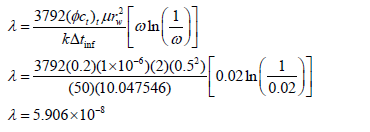
3.3. Field example, homogeneous reservoir
[10] provided a field case which input information is given in Table 1 and production vs. time is given in the semilog plot of Fig. 8. Using the permeability, given in Table 1, the slope was estimated from Eq. 36 to be 1.42x10^-5 D/STB/cycle. With the first point in Fig. 8 and the intercept (1/q)1hr of 9.57x10^-5 D/STB, the parameters x and y are estimated using Eqs. 32 and 36, respectively, such as

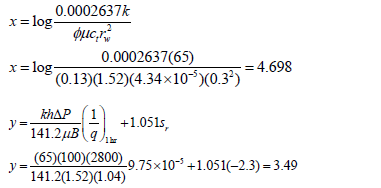
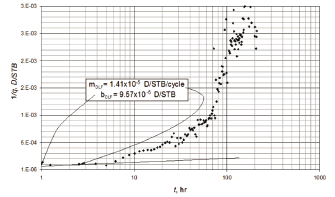
Figure 8. Semilog plot of reciprocal rate versus time for the field example

Then, Eq. 31 allows for one to obtain a value of the dimensionless storativity coefficient w of 0.06. From Fig. 9, the slope m_DLF = 1.362x10-4 D/STB/hr0.5 and intercept b_DLF = 1.307x10-4 D/STB allow for one to determine reservoir width and geometrical skin factor, respectively, from Eqs. 21 and 22

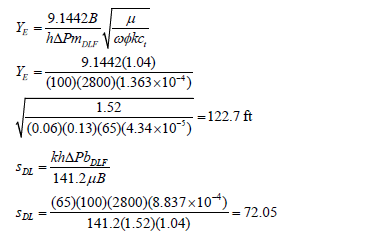
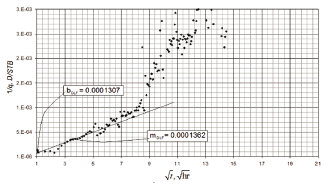
Figure 9. Cartesian plot of the reciprocal rate versus the square root of time for field example

Again, Eq. 37 is used to estime l,

 

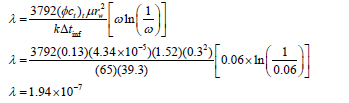
4. ANALYSIS OF RESULTS

It is observed from the simulated examples that the estimated parameters obtained with the equations developed in this study agree quite well with the input data. However, for the case of a heterogeneous reservoir there is a need to obtain the mechanical skin factor from other sources, so that, dimensionless storativity coefficient, w, which is also required for estimating the skin factor, can be estimated from the correlation (Eq. 31) developed in this study. This manipulation was performed in the field case example. The Warren and Root parameters estimated in this paper do not agree well with those estimated by [10]; however, we consider that they are in an adequate range since these parameters can be within a difference of one order of magnitude.

 

5. CONCLUSION

The straight-line conventional method for rate-transient analysis was complemented with new equations for long and narrow homogeneous and naturally fractured reservoirs. The equations were successfully applied to synthetic examples. A field example for a heterogeneous reservoir was presented to demonstrate the application of the proposed solution.

 

ACKNOWLEDGMENTS

The authors are grateful to the most Holy Trinity and Mary the Virgin, the holy mother of God. The authors also thank Universidad Surcolombiana and Ecopetrol-ICP for providing support for the completion of this work. We strongly thank Dr. Taufan Marhaendrajana for providing the field example to us.

 

NOMENCLATURE

 

REFERENCES

[1] Escobar, F.H., Hernández, Y.A. and Hernández, C.M., Pressure Transient Analysis for Long Homogeneous Reservoirs using TDS Technique. Journal of Petroleum Science and Engineering. Vol. 58, (1-2), pp. 68-82. 2007.         [ Links ]
[2] Escobar, F.H., Muñoz, O.F., Sepulveda, J.A. and Montealegre, M., New Finding on Pressure Response In Long, Narrow Reservoirs. CT&F – Ciencia, Tecnología y Futuro. Vol. 2 (6), 2005.         [ Links ]
[3] Escobar, F.H. and Montealegre, M., Effect of Well Stimulation on the Skin Factor in Elongated Reservoirs. CT&F – Ciencia, Tecnología y Futuro. Vol. 3 (2), pp. 109-119. Dec. 2006.         [ Links ]
[4] Escobar, F.H. and Montealegre, M., A Complementary Conventional Analysis For Channelized Reservoirs. CT&F – Ciencia, Tecnología y Futuro. Vol. 3 (3), pp. 137-146. Dec. 2007.         [ Links ]
[5] Escobar, F.H., Petroleum Science Research Progress. Nova Publishers. Edited by Korin L. Montclaire. Chapter title Recent Advances in Well Test Analysis for Long an Narrow Reservoirs. 2008.         [ Links ]
[6] El-Banbi, A.H. and Wattenberger, R.A., Analysis of Linear Flow in Gas Well Production. Paper SPE 39972 Gas Technology Symposium, Alberta, Canada, March, pp. 15-18. 1998.         [ Links ]
[7] Escobar, F.H., Hernandez, D.P. and Saavedra, J.A., Pressure and Derivative Analysis For Long Naturally Fractured Reservoirs Using The TDS Technique. Dyna, Year 77, (163), pp. 102-114. 2010.         [ Links ]
[8] Warren, J.E. and Root, P.J., The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. Sept, pp. 245-255. 1963.         [ Links ]
[9] Tiab, D. and Escobar, F.H., Determinación del Parámetro de Flujo Interporoso a Partir de un Gráfico Semilogarítmico. X Congreso Colombiano del petróleo. Bogotá, Colombia, pp. 14-17, 2003.         [ Links ]
[10] Marhaendrajana, T., Blasingame, T.A. and Rushing, J.A., Use of Production Data Inversion to Evaluate Performance of Naturally Fractured Reservoirs. Paper SPE 90013, SPE International Petroleum Conference in Mexico held in Puebla, pp. 8-9, Nov. 2004.         [ Links ]