APLICACIÓN DEL MÉTODO DEL INTERVALO DE CONFIANZA COMO TÉCNICA GEOESTADÍSTICA NO LINEAL A LA MODELACIÓN ESPACIAL DE VARIABLES GEOTÉCNICAS

IMPLEMENTATION OF THE CONFIDENCE INTERVAL APPROACH AS GEOSTATISTICAL NONLINEAR MODELING FOR SPACE GEOTECHNICAL VARIABLES

 

LUÍS HERNÁN SÁNCHEZ ARREDONDO
Profesor Asociado, Universidad Nacional de Colombia Facultad de Mina, slhsanche@unalmed.edu.co

GLORIA ISABEL RAMÍREZ BOLÍVAR
Ingeniera geóloga , Estudiante de Maestría en Ingeniería Geotécnica, Gloria.ramirez@medelli.gov.co

 

Recibido para revisar Mayo 13 de 2011, Aceptado Marzo 23 de 2012, versión final Marzo 30 de 2012

 

---

RESUMEN: El presente trabajo tuvo como objetivo elaborar la cartografía automática de algunas las propiedades físico - mecánicas del suelo en un sector del Barrio Laureles de la ciudad de Medellín, Colombia.

Como método de estimación se utilizó principalmente la técnicas geoestadísticas conocido como "Intervalo de Confianza", el cual fue desarrollado por la Escuela de Minas de París. La base de datos corresponde a una de las empresas de ingeniería geotécnica de la ciudad, los cuales han sido recopilados entre los años 1993 y 2005, extrayendo información relacionada con los ensayos de penetración estándar NSPT, humedad natural del suelo y compresión simple Qu. Para la evaluación geoestadística de los datos se realizaron las etapas de análisis exploratorio, análisis estructural, estimación, simulación, e implementación del intervalo de confianza. El método del intervalo de confianza es muy útil para analizar variables de libre distribución estadística y en este caso pudimos obtener los posibles valores extremos para las variables arriba mencionadas.

PALABRAS CLAVE: Geoestadística, geotecnia, intervalo de confianza, kriging.

ABSTRACT: This study aimed to primary work computer mapping of some of the physical - rnechanical properties of soil in an area of Barrio Laureles -Medellín Colornbia.

As the estimation method it was mainly used the geostatistical technique known as "confidence interval", which was developed by the Ecole des Mines de Paris. The database corresponds to one of geotechnical engineering firms in Medellin city, which have been collected between 1993 and 2005, extracting information related to the standard penetration tests NSPT, natural soil moisture and compressive Qu. For geostatistical data assessment were carried out exploratory stages of analysis, structural analysis; estimation, simulation, and implementation of the confidence interval. The confidence interval method is very useful for analyzing the statistical distribution of free variables, in this case it was able to identify any extreme values for the variables mentioned above

KEYWORDS: Geostatistics, geotechnical, confidence interval, kriging

---

 

1. INTRODUCCIÓN

1.1 Ubicación del área de estudio
Como se aprecia en la figura 1, la zona de interés para este proyecto se localiza en el sector comprendido entre las carreras 65 y 83 y entre las calles 33 y 44, del Barrio Laureles de la ciudad de Medellín, Departamento de Antioquia, correspondiente a las coordenadas Este 830.421 - 833.490 y Norte 1.181.613 - 1.183.304, de acuerdo al sistema coordenado Transverse Mercator con origen de coordenadas Bogota - Colombia.

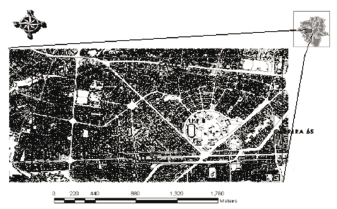
Figura 1. Localización zona de estudio, tomado del Sistema de Información Geográfico para Medellín, SIGAME

Este sector es uno de los principales sitios de desarrollo urbanístico en la ciudad debido principalmente a su entorno comercial y su topografía suave.

1.2. Formaciones superficiales
Para la zona en estudio los estratos de suelo se componen principalmente de suelos limosos y arcillosos asociados a depósitos no litificados. La información existente de perforaciones de la zona no tiene una descripción geológica de las muestras, lo cual es una de las principales falencias de las suposiciones realizadas para la zona, ya que en este caso no permite identificar diferentes estratos de origen geológico, sin embargo, como punto a favor se tiene que las clasificaciones que se tienen de los materiales existentes identifican principalmente suelos fino granulares que varían entre limos y arcillas (ML, MH, CL y CH) con algunos lentes de materiales gruesos (SM).

En general se tiene el predominio de este tipo de materiales en toda la zona, los cuales se detectan desde la superficie hasta la máxima profundidad explorada y clasificada (17.45 m). Por otro lado, los depósitos aluviales del río Medellín han sido cubiertos por depósitos de flujo de lodo, como es el caso de la zona en estudio, donde se demarca de acuerdo a la información existente en la Microzonificación Sísmica del Valle de Aburrá [1], el cambio entre ambas formaciones (Depósitos aluviales y flujos de lodos).

Para la hipótesis de trabajo se consideró la existencia de suelos fino granulares, sin embargo, es necesario considerar que la diferencia en los ambientes de depositación de estos materiales genere una mayor variabilidad en el análisis de los datos o incluso repercuta en poblaciones diferentes.

1.3 Base de datos existente
La base de datos proviene de diversos estudios de suelos realizados en la zona por parte de una empresa de Ingeniería Geotécnica, la cual fue igualmente usada para trabajos de investigación en el área de geotecnia de la Universidad Nacional de Colombia.

En general esta base de datos posee información de la ubicación de la perforación con dirección catastral, por su parte la información geotécnica presenta datos tales como la profundidad de la muestra, resultados del ensayo SPT a dichas profundidades, ensayo de humedad y resistencia a la compresión simple. Las coordenadas para cada una de las perforaciones debieron ser asignadas mediante la georeferenciación de las mismas.

Las perforaciones poseen profundidades entre 7 y 15 metros, con muestras tomadas mediante tubo partido Split Spoon y/o Shelby, con muestreo cada 1.50 metros en toda la longitud de la perforación. Así mismo, se posee información relacionada con las propiedades del suelo como son la humedad para la mayoría de las profundidades, resistencia a la compresión simple a profundidades especificas de 2.30 y 3.30 metros, así como limites Atterberg, lavados sobre el tamiz 200 y clasificación a profundidades especificas, aunque estos últimos datos no se tienen para todas las perforaciones, por lo que no se utilizan para el análisis geoestadístico.

1.4. Método del intervalo de confianza para estimaciones locales
Si se representa una variable de interés como Z(x) la estimación de la misma por un método como el Kriging se designa como 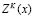y la desviación estándar del kriging como 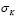. El error en la estimación corresponde a la diferencia entre el valor real y el estimado Z(x) - 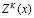. Al obtener los intervalos de confianza estándar se asume que el error de la estimación es normalmente distribuido, en este caso el intervalo de confianza para una probabilidad del 95% se da por la expresión:

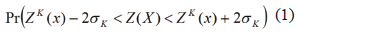
Donde es la probabilidad media, sin embargo, en general la distribución normal del error es bastante rara en la naturaleza, lo que genera inconsistencias en el manejo de la información.

Consistentes con lo anterior los autores Chris Roth y Margaret Armstrong [2] del Centro de Geoestadística de Fontainebleau (Francia), definieron que para encontrar el intervalo de confianza de una distribución lognormal,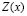 se debe realizar primero la transformación dicha distribución a normal 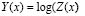y luego en ésta obtener los intervalos utilizando la desviación estándar. [2]

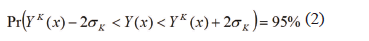
Devolviéndonos en la transformación la expresión anterior queda:

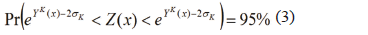
Para la transformación de los datos se utiliza una expresión matemática perteneciente a la técnica Geoestadística No Lineal, correspondiente a la anamorfosis gausiana.

1.4.1. Anamorfosis Gaussiana
Este corresponde al primero de los pasos de la transformación de cada una de las variables en su normal equivalente. Esta transformación se obtiene en la correspondencia entre el histograma acumulado de cada una de las variables y el normal equivalente. En este caso para cada valor de las variables en este caso resistencia a la penetración NSPT, resistencia a la compresión Simple Qu y Humedad, definidas como (zo) se obtiene el equivalente gaussiano (y0).

 

2. ANÁLISIS EXPLORATORIO DE LAS VARIABLES

La finalidad del Análisis Exploratorio de Datos es examinar los datos previamente para conseguir una comprensión básica de los mismos y de las relaciones existentes entre las variables analizadas [3]. El análisis geoestadístico se realizó mediante el software ISATIS V9, de propiedad de la Universidad Nacional.

Análisis univariado: En este caso el análisis se orienta a describir el tipo de distribución de frecuencias y su grado de similitud con relación a una distribución normal que deben presentar los datos. Para esto se utilizó el análisis gráfico, medidas de la amplitud, de tendencia central, de variabilidad y de estructura.

Las propiedades geotécnicas de resistencia a la penetración estándar NSPT, resistencia a la compresión simple Qu y humedad, serán de ahora en adelante las variables analizadas.

En la figura 2, se muestra la representación en el espacio 2D, para la variable NSPT.

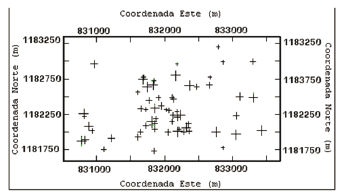
Figura 2. Localización datos en un plano xy y zx para la variable NSPT

Como resumen del análisis exploratorio de los datos se presenta la tabla 1, donde se consideran las condiciones de amplitud, tendencia central, variabilidad y estructura.

Tabla 1. Caracterización estadística de los datos de ensayo NSPT (golpes por pie), Compresión Simple Qu (Kg/cm2) y humedad (%)

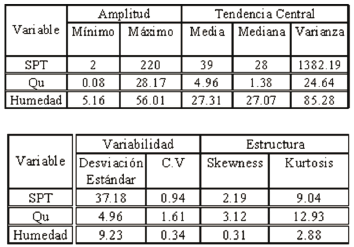
Respecto a la tendencia central de los datos en la variable NSPT tienen una relación mediana/media con un valor de 0.20, lo que muestra una diferencia de 80% frente a un valor ideal de normalidad, lo que por sí solo no es suficiente para decidir si los datos presentan una distribución no normal.

Con relación a la variabilidad de los datos respecto a su tendencia central, se observa en esta misma variable una variabilidad alta (coeficiente de variación de 94%), este hecho puede ser explicado por las características naturales de los atributos ó por problemas de representatividad de los datos.

Al nivel de la estructura, se observa un valor de Coeficiente de sesgo (skewness) de 2.19, el cual al ser mayor que 1 indica un desplazamiento de la distribución hacia la izquierda respecto al valor medio de 39 golpes por pie.

Para la variable Qu, la relación de tendencia central de los datos mediana/media toma un valor de 0.27, con lo que se determina una diferencia de 73% frente a un valor ideal de normalidad. Con relación al coeficiente de variación se tiene que presenta un valor superior al 100%, lo cual indica una alta variabilidad de los datos. Respecto a la estructura, se presenta un valor de coeficiente de sesgo de 3.12 que indica es un desplazamiento de la gráfica de frecuencia hacia la izquierda con respecto al valor medio de la resistencia que sería de 4.76 Kg/cm2.

Para la variable humedad la tendencia central de los datos muestra una distribución del histograma muy cercana a la normal, la cual se corrobora en la relación mediana/media que alcanza un valor de 0.99, muy cercano a la unidad el cual es el valor ideal para una distribución de este tipo.

Con relación a la variabilidad de los datos respecto a su tendencia central, se observa que la variable humedad presenta una variabilidad media, tal como lo evidencia el coeficiente de variación del 34%, lo que se explica debido a las características naturales de esta variable. En este caso es necesario considerar que la variable analizada fue tomada en un intervalo de tiempo que incluye diferentes épocas de lluvias y épocas secas y que esta variable depende directamente del periodo en el cual es tomada, en especial si se tiene en cuenta el posible ascenso y descenso del nivel freático en la zona y sus efectos en el contenido de humedad natural del suelo.

Al nivel de la estructura de los datos para esta variable presenta un valor de coeficiente de sesgo (skewness) de 0.31, lo que indica un ligero desplazamiento del histograma hacia la derecha de las frecuencias respecto al valor medio de la variable, la cual es en este caso del 27.31%.

Por otro lado, se analizaron los diagramas de cuantíles en los cuales se comparan en un sistema de coordenadas cartesianas los cuantíles muestrales en el eje X con los cuantíles esperados bajo la hipótesis normalidad en el eje y. Si la distribución de partida es normal dichos diagramas tenderán a ser rectas y pasaran por el origen [4]. Cuanto más se desvíen de una recta esta gráfica, menos normales serán los datos, para el caso en estudio, el gráfico cuantil para los datos originales de la variable NSPT muestra una una distribución no normal de estos datos.

Para la variable resistencia a la compresión simple Qu, el gráfico intercuantil para los datos originales muestra que los datos posee una distribución no normal, indicando el sesgo hacia izquierda que presentan los mismos, esta distribución evidencia condición de lognormalidad de los datos originales, tanto para la variable Qu como NSPT .

En cuanto a la variable humedad, se tiene que esta gráfica evidencia una distribución simétrica ó muy cercana a la normalidad; sin embargo, hacia los extremos se presentan algunos problemas, no obstante se decide trabajar con los datos sin transformar para esta variable, considerando que una transformación logarítmica no traería mayores beneficios.

 

3. ANÁLISIS ESTRUCTURAL

Para la estimación del variograma experimental de cada una de la variables, se estimó inicialmente el  variograma medio, global  u "omnidireccional" que es el que se presenta en la figura 3 y como su nombre lo indica no depende de la dirección solamente sino de la magnitud de h, el cual proporciona una idea inicial de la variabilidad espacial de los datos, siendo este variograma el más idóneo para representar u obtener una estructura clara y definida para cada una de las variables, sobre todo en el estudio que nos atañe; donde se posee poca información.

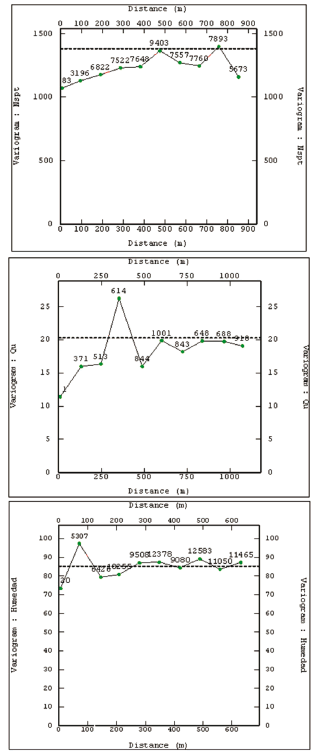
Figura 3. Variograma experimental variable sin transformar de las variables ensayo NSPT, ensayo la compresión Simple Qu, y humedad

3.1. Modelación de la función de correlación espacial
La modelación del variograma consiste en buscar una función analítica que represente adecuadamente los valores estimados del variograma, ésta continúa con un proceso de prueba y error de manera visual, modificando los parámetros del modelo hasta obtener un compromiso razonable. Este procedimiento es conocido como el ajuste a sentimiento [5], el cual consiste en seleccionar los parámetros del variograma teniendo en cuenta una serie de consideraciones de tipo cualitativo tales como:

• El modelo ajustado refleje los principales aspectos del variograma experimental. No se debe intentar ajustar los mínimos detalles, ya que en general estos no son una característica del verdadero variograma sino más bien fluctuaciones naturales.
• El valor del efecto pepita puede ser obtenido extrapolando los primeros puntos del variograma experimental hasta corte el eje de las ordenadas.
• Pueden considerarse modelos compuestos.

Considerando lo anterior se procedió a trabajar con el variograma omnidireccional, ya que es de esperarse que este presente una estructura mas clara e interpretable. Para cada una de las variables analizadas, se consideraron al menos el ajuste de dos modelos de variograma.

Para las variables analizadas se trabajaron como variogramas teóricos, el esféricos, exponencial y gaussiano, combinados con el efecto pepita.

3.2 Validación cruzada
El ajuste de los variograma experimentales, siempre trae incertidumbres sobre las hipótesis de estacionariedad y los modelos seleccionados entre otras, las cuales contribuyen al error en la estimación. Es así como una forma para diagnosticar algunos problemas en el ajuste obtenido es la validación cruzada, cuya idea básica es borrar un dato para predecir las observaciones borradas. Si el modelo teórico escogido es bueno o describe adecuadamente la dependencia espacial el valor predicho será cercano al verdadero.

Para este trabajo se consideró como criterios objetivos de evaluación el Error Promedio Estandarizado el cual de debe ser de 0 (cero), la Varianza Estándar del Error, la cual debe ser de 1 (uno) y el numero de datos rechazados que no debe superar el 5.

Los resultados obtenidos de la validación cruzada para los datos transformados, se presentan en la tabla 2.

Tabla 2. Resultados del análisis de validación cruzada para las variables de SPT y Compresión Simple Qu transformada

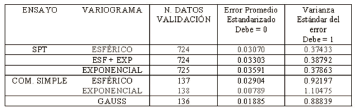
Producto del análisis de estos resultados se obtiene que el modelo teórico que mejor representa el fenómeno de resistencia a la penetración estándar NSPT (datos transformados) es el modelo esférico, por su parte, la variable resistencia a la compresión simple (Qu) (datos transformados) se modela con el variograma exponencial.

Para la variable humedad no se trabaja transformaciones, debido al comportamiento aparentemente normal de los datos.

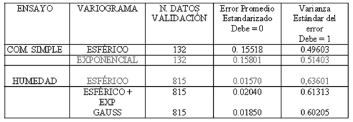
En cuanto a los datos sin transformar para las variables de resistencia a la compresión simple (Qu) y humedad, se tienen que el proceso de validación cruzada encuentra que los variogramas teóricos que representan el fenómeno en este caso son el exponencial y el esférico respectivamente.

La variable NSPT se trabaja con el variograma teórico esférico. En la tabla 3, se resumen el resultado del proceso de validación cruzada para las variables sin transformar.

Tabla 3: Resultados del análisis de validación cruzada para la variable de Compresión Simple Qu y Humedad sin transformar

 

4. KRIGING ORDINARIO ESTÁNDAR

Una vez realizado el análisis estructural de los datos se procede a conseguir una superficie de estimación, uno de los métodos clásicos de estimación lineales es el Kriging Ordinario Estándar, el cual considera, la distancia entre los puntos, el peso de los puntos y la estructura espacial del fenómeno que representan.

A las variables de trabajo sin transformar se les realiza una estimación utilizando el método del Kriging ordinario estándar, el resultado de esta estimación es un mapa 3D para cada uno de las variables. Los resultados presentados para el ensayo de penetración NSPT, evidencian una estratigrafía compleja en la zona, marcando sectores con resistencias a la penetración bajas a muy bajas las cuales se presentan de forma superficial, seguida por capas en las cuales se observa un incremento en la resistencia con la profundidad. Se tiene igualmente zonas con valores altos en la resistencia del suelo NSPT en la superficie, la cual se reduce con la profundidad.

Lo anterior evidencia una estimación en la cual no existe una tendencia general del incremento de la resistencia con la profundidad, cabe resaltar que estudios geoestadísticos realizados en el Brasil [6], se ha considerado dicho incremento de la resistencia como una tendencia que afecta la correlación, no obstante se considera importante tener en cuenta dicha tendencia en futuras investigaciones.

En la zona oriental de la zona en estudio o zona cercana al río Medellín (extremo oriental del bloque 3D) se obtuvo la estimación de una franja de valores medios, que contrasta con otra de valores altos a la misma profundidad. Este contraste es posiblemente asociado el aluvión existente en este sector y el contacto con los depósitos de flujo.

Del análisis del bloque 3D estimado, se observa lo que representa un problema en el modelo de superficie como es la generación de un incremento de la resistencia del suelo en forma horizontal, no paralela a la superficie del terreno donde se realiza el estudio, lo cual puede ser difícil de explicar con modelo geológico en la zona, donde se espera una disposición de capas subparalelas a la superficie, lo cual es propia de un fenómeno de depositación en este caso una ladera de muy baja pendiente no horizontal, por lo que las propiedades del suelo deben igualmente considerar la disposición de los estratos existentes en la zona.

Para la viable resistencia a la compresión simple Qu, la superficie de estimación obtenida mediante el sistema de kriging ordinario muestra como la estimación se ve afectada por la limitación de datos, lo que genera un mapa en 3D con mucho más espacios vacíos y menos información que la generada con el ensayo SPT, concentrando la zona con mayor información en la parte central del área de estudio. Cabe recordar que los datos suministrados en este caso corresponden a perforaciones con solo dos valores del ensayo a profundidades de 2.30 y 3.30 metros, lo que limita lucho más la profundidad de la estimación.

En este caso los datos estimados difieren de una estratigrafía clara como la observa en el ensayo NSPT.

Respecto a la variable Humedad, se tiene que en general la estimación presenta una tendencia a disminuir el valor de la misma con la profundidad; sin embargo, se deben recordar las variaciones que son imputables a la medida de este parámetro, lo que puede alterar la modelación de su variabilidad espacial. Así mismo, el efecto de periodicidad en este caso de los datos genera problemas ya que, por así decirlo se están considerando varios escenarios (periodos húmedos y secos)

 

5. MÉTODO DEL INTERVALO DE CONFIANZA PARA ESTIMACIONES LOCALES

La aplicación del método del intervalo de confianza considera la siguiente metodología:

• Se transforman los datos de cada una de las variables mediante una función de anamorfosis y se haya la función equivalente gaussiana.
• Obtenida esta función equivalente se calcula el variograma experimental para la misma y el modelo de variograma asociado.
• Se obtiene el kriging y para cada bloque creado, se adquiere el kriging (estimación gaussiana) y la correspondiente varianza del kriging. En este caso se trabaja con bloques los cuales se caracterizan por tener menor varianza y menos sesgo.
• Obtenido éste se utiliza la estadística estándar para construir el IC alrededor del valor del bloque gaussiano.

5.1 Función de anamorfosis
Se obtiene dibujando los valores acumulados de la variable en el eje y, contra el correspondiente equivalente gaussiano en el eje x. Para cada una de las variables analizadas las funciones de anamorfosis fueron halladas, obteniendo que su forma cóncava es característica de variables con un sesgo positivo.

Para el caso de la variable resistencia a la compresión simple Qu, se presenta una situación similar a que la que registra la variable NSPT en cuanto a la forma que presenta su función de Anamorfosis.

Para la variable Humedad la función de Anamorfosis correspondiente presenta una concavidad menor, lo que comprueba la cercanía a la normalidad de esta variable, la cual que presenta un ligero sesgo positivo.

Continuando con la metodología propuesta se obtiene el kriging y para cada bloque, la técnica de Kriging que se usa es la Simple, ya que la variable tiene media conocida que en este caso es cero.

 

6. RESULTADOS

Como resultado se obtienen los mapas en tres dimensiones del intervalo de confianza inferior y superior de cada una de las variables. Con el fin de tener un criterio comparativo se analizan los limites para cada una de las variables analizas en un corte ó sección a la cota 1485 para la variable NSPT, 1480 para la variable Qu y 1485 para la variable humedad.

En el caso de la variable NSPT, se observa que el límite inferior está entre los 10 y 19 golpes por pie, mientras que el límite superior está entre 30 y 120 golpes por pie tal como se aprecia en la figura 4.

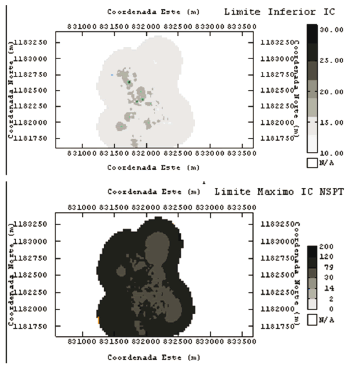
Figure 4. Lower and Upper Limit Limit IC NSPT variable

Para la variable Qu en la figura 5, se presenta el límite inferior y superior a una profundidad definida en la cota 1480, en este caso se tiene una sección donde se muestra para cada uno de los puntos, cual es el valor el mínimo y máximo obtenido para la variable, es así como se tienen sectores donde el valor mínimo obtenido a dicha profundidad está entre 0.44 y 0.47 Kg/cm2 y el máximo se encuentra entre 11.61 y 11.96 Kg/cm2. Para los datos obtenidos en el limite inferior por encima de 2.15 Kg/cm2, se presenta un salto importante, lo que representa algunos problemas asociados a la escasa cantidad de datos con lo que se trabaja y a la presencia de valores anormalmente altos.

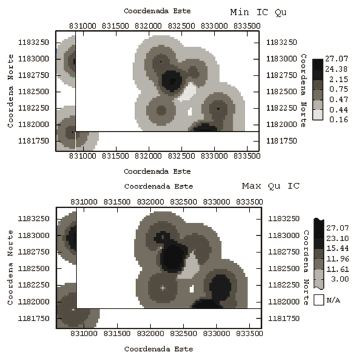
Figura 5. Límite Inferior y Límite Superior del IC de la variable Qu

Para la variable humedad, la figura 6, presentan los límites inferior y superior del intervalo de confianza para cada uno de los sitios donde se obtuvo información, en este caso un punto ubicado dentro de las zonas claras en ambas imágenes presenta un valor mínimo de la humedad de entre 21 y 30% y un valor máximo entre 34 y 39%.

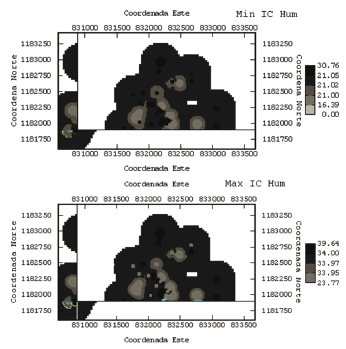
Figura 6. Límite Inferior y Límite Superior del IC de la variable Humedad

7. ANÁLISIS DE LOS RESULTADOS

Con base en el intervalo de confianza calculado y tendiendo en cuenta la metodología propuesta por Amstrong y Roth [2] se puede conocer la posición relativa de los datos obtenidos en el caso de la estimación del kriging ordinario. Es así como la posición relativa de los datos se denomina RPv y corresponde a:

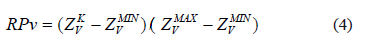
Se dice que la estimación del bloque cae dentro del intervalo de confianza no lineal, si 0 < RPv < 1. Cuando la estimación del bloque está por debajo de cero se dice que está por debajo del intervalo de confianza y mientras que si cae por encima de 1, se dice que está por encima del intervalo de confianza. En la figura que se presenta a continuación se observan la ubicación relativa de los datos obtenidos con el Kriging ordinario para cada una de las variables, dentro de los respectivos intervalos de confianza obtenidos.

En la variable NSPT se tiene que para los datos estimados mediante el kriging ordinario, la mayor parte se encuentran por encima del intervalo de confianza, mientras que un bajo porcentaje se encuentran por debajo de los mismos. De los datos estimados solo un pequeño porcentaje se encuentra dentro del intervalo de confianza correspondiendo a los datos entre 0 y 10 golpes por pie.

Para la variable Qu Resistencia a la compresión simple, se observa que parte los datos se encuentran en el límite inferior del intervalo de confianza o son menores de este, es decir que se encuentran por fuera del intervalo, lo que indica la baja confiabilidad de los datos encontrados. Esto explica la estratigrafía compleja que define la estimación en 3D realizada con el Kringing Ordinario (KO).

En cuanto a la variable humedad se tiene que presenta una situación similar a la de la variable NSPT, sin embargo, en este se observa una gran cantidad de datos provenientes de la estimación por debajo del intervalo de confianza inferior. Igualmente para la variable humedad los valores entre 20 y 35% de humedad se encuentran dentro del intervalo de confianza.

 

8. CONCLUSIONES

La ingeniería geotécnica por su naturaleza exige herramientas para hacer frente a grandes incertidumbres y variaciones en las propiedades del material. Una de estas herramientas y que este articulo ha tratado de adoptar para el caso especifico de la Ciudad de Medellín, es la geoestadística, la cual ha demostrado en otros lugares del mundo ser una herramienta de gran importancia en el proceso de interpretación de la información geotécnica disponible a diferentes escalas, evidenciando algo que se debe considerar siempre que se hacen análisis del suelo como es la variabilidad espacial de sus propiedades.

El efecto pepita que presentan todos los modelos analizados para cada una de las variables, es muy alto, los cual se debe a la suma de errores atribuible al origen de los datos. Para el caso del ensayo de penetración estándar NSPT se puede considerar la acción humana en la ejecución del ensayo la que puede generar incrementos en la variabilidad, en cuanto a la variable Qu, presenta como origen de este efecto condiciones tales como el tipo de muestreador usado para la toma de la muestra de suelo, el procedimiento de toma y en particular con las dimensiones del muestreador en relación con el espesor de su pared, las cuales generan alteraciones en la calidad de la muestra y variaciones en las condiciones de esfuerzos y deformaciones dentro de la misma. Igualmente se considera el proceso de extracción de las muestras en el laboratorio lo cual genera cambios de esfuerzos. En cuanto a la variable humedad del suelo se tienen las diferencias que se aceptan en este ensayo en relación al laboratorio una de las principales causas para el efecto pepita.

La caracterización geoestadística de la variable NSPT provee estimaciones que en general podrían considerarse buenas debido a la gran cantidad de información que se genera, no obstante dichas estimaciones para el caso del Kriging Ordinario, resulta conservadora al compararse con otro método de estimación como es el Kriging Lognormal. Al analizar la ubicación de los datos obtenidos mediante el Kriging Ordinario Estándar dentro del intervalo de confianza obtenido se evidencia que de estos datos solo se consideran dentro del intervalo los que se encuentra entre 10 y 100 golpes por pie.

Respecto a las variables Qu y Humedad las estimaciones obtenidas presentan mucha menor información, los cual se asocia a la escasez de datos como es el caso de la variable Qu y al alto efecto pepita que presenta la variable humedad que repercute en una alta variabilidad de los mismos.

El análisis de los datos obtenidos mediante el método de Kriging Ordinario Estándar en este caso a la luz del intervalo de confianza obtenido, permite concluir que para la variable Qu, la escasa información obtenida se encuentra por debajo del límite inferior o incluso sobre dicho límite, lo que admite considerar estos datos como poco confiables, evidenciando la necesidad de un mayor número de datos si se quiere obtener información confiable de esta variable.

Respecto a la variable de humedad se tiene que de los datos estimados se encuentran dentro del intervalo de confianza solo los que se encuentra 15 y 30%.

En general el análisis geoestadístico realizado para estimar los valores de variables como los analizadas en este caso derivan en una información valiosa en la ingeniería geotécnica, siempre y cuando se conozcan las limitaciones de la información generada, es por esto que definir un intervalo de confianza o realizar la comparación entre los datos obtenidos de estimación y simulación, permite conceptualizar los datos obtenidos y la confiabilidad y cercanía a la realidad de los mismos.

 

REFERENCIAS

[1] Microzonifiación Sísmica del Valle de Aburrá, Área Metropolitana del Valle de Aburrá, 2009.         [ Links ]
[2] Roth, C. and Armstrong, M., Confidence Intervals for Local Estimation: Aplication to the Witwatersrand Basin, Centre de Geostatistique, France.         [ Links ]
[3] Miranda, M., Alfonso, R., Condal, Importancia del Análisis Estadístico Exploratorio en el Proceso de Interpolación Espacial: caso de estudio reserva forestal Valdivia, v.24 n.2 valdivia ago. 2003. disponible en web: http://www.scielo.cl/scielo.php?pid=s0717-92002003000200004&script=sci_arttext. [consulta 28 octubre 2009]         [ Links ]
[4] Montero, L., Larraza, B., Introducción a la geoestadística Lineal, 2008, disponible en web: www.books.google.com.co         [ Links ]
[5] Figueras, S. y Gargallo, P., "Análisis Exploratorio de Datos", disponible en web: 5campus.com, Estadística <http://www.5campus.com/leccion/aed> [consulta 28 febrero 2010]         [ Links ]
[6] FOLLE, D., ANALISE E Aplicaciones da Geoestadísticas no contexto geológico – geotécnico urbano, (2009), disponible en web: www.lume.ufrgs.br/handle/10183/15707 [diciembre 2009]         [ Links ]
[7] Londoño, L. A., Ramírez, J. R., Ramírez, G. I., Ordóñez, C. A., Modelo de interpolación espacial mediante sistemas de información geográfica para el estudio de la variabilidad espacial de la resistencia a la penetración del suelo, DYNA vol 7 # 164.         [ Links ]