Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.79 n.173 Medellín maio/jun. 2012
REVISIÓN DE MODELOS CONSTITUTIVOS PARA CARTÍLAGO ARTICULAR
REVIEW OF CONSTITUTIVE MODELS FOR ARTICULAR CARTILAGE
PEDRO J. CABALLERO
Ing. M., Grupo de Investigación en Diseño Óptimo Multidisciplinario, Universidad Nacional de Colombia, Bogotá. pjcaballeroa@unal.edu.co
NELSON ARZOLA
Dr., Grupo de Investigación en Diseño Óptimo Multidisciplinario, Universidad Nacional de Colombia, Bogotá. narzola@unal.edu.co
Recibido para revisar Mayo 9 de 2011, aceptado Enero 19 de 2012, versión final Febrero 13 de 2012
RESUMEN: Se presenta una revisión de varios modelos utilizados para explicar el comportamiento mecánico del cartílago articular. La revisión hace énfasis en modelos mecánicos ya que los modelos físico químicos desbordan el alcance del análisis de sólidos que se quiere tratar. La mayoría de los modelos revisados retoman la idea planteada por Mow, la cual plantea que este tipo de tejidos puede ser modelado como un material bifásico, en donde cada fase tiene sus características específicas y la interacción entre ellas brinda las propiedades mecánicas del tejido como un global. El planteamiento de un modelo fenomenológico para el cartílago articular es complejo debido a la naturaleza de la respuesta bajo cargas transitorias y a los fenómenos físico químicos acoplados que tienen lugar. Los modelos futuros deberán estar orientados a considerar integralmente dichas características e interacciones.
PALABRAS CLAVE: Cartílago articular, modelo constitutivo, viscoelasticidad, teoría bifásica.
ABSTRACT: In this article, a review of several models used to explain the mechanical behavior of the articular cartilage is presented. This review makes an emphasis on the mechanical models because the physical-chemical models are out of scope of the solid behavior analysis explained in this study. Most of the revised models retake the idea proposed by Mow which states that this type of tissues can be modeled as a biphasic material where each phase has got its specific characteristics and the interaction among these phases offers the tissue overall mechanical properties. The approach of a phenomenological model for an articular cartilage is complex due to the nature of the transitory loads answer and bonded physical-chemical phenomena. The future models will have to be oriented to consider, in an integrated way, these characteristics and interactions among them.
KEYWORDS: Articular cartilage, constitutive model, viscoelasticity, biphasic theory.
1. INTRODUCCIÓN
El cartílago articular, así como la mayoría de los tejidos biológicos, presenta un comportamiento mecánico difícil de simular mediante los modelos constitutivos de los materiales de ingeniería más comunes. Por ello, se han dedicado muchas investigaciones y esfuerzos en aproximar el comportamiento que este exhibe por medio de nuevos modelos constitutivos. Comprender el comportamiento del cartílago articular es importante para poder analizar y estudiar los fenómenos de degradación que actúan en estos tejidos y su influencia en procesos patológicos [1]. El cartílago es un tejido de alta importancia en las articulaciones sinoviales lo que ha hecho necesario el desarrollo de técnicas quirúrgicas y de rehabilitación para resolver los problemas que lo afectan (la mayoría de remplazo protésico) [2][3], a la par con la generación de técnicas de simulación orientadas a las articulaciones comúnmente afectadas [4–8], así como a las prótesis a utilizar [9].
El cartílago tiene tres funciones básicas dentro del complejo articular, todas de naturaleza mecánica [10], siendo este el principal tejido que sufre en la artropatía de la osteoartrosis [11]. El cartílago posee superficies lisas que facilita el desplazamiento entre los huesos en conjunción con el líquido sinovial. Además, distribuye las cargas y evita que exista concentración de esfuerzos en la superficie del hueso subcondral. Es importante resaltar que la acción del líquido sinovial como lubricante reduce drásticamente la fricción, aún cuando la articulación se encuentra sometida a una sobrecarga fisiológica [12].
El cartílago articular es el elemento que brinda la característica viscoelástica de las áreas que intervienen en las articulaciones sinoviales. A diferencia de los huesos, posee una limitada capacidad de regeneración [13], lo que significa una irrecuperable condición de normalidad una vez el proceso de degradación empieza a darse. Esta degradación puede ser por enfermedades, tanto congénitas como adquiridas [14], así como procesos biológicos que modifiquen las propiedades físicas del cartílago sano o por traumatismos que afectan la integridad del tejido.
El cartílago articular se encuentra como una delgada capa que recubre los extremos de los huesos que hacen contacto en la articulación. Es un tipo especializado de tejido conectivo, conformado por células llamadas condrocitos encargados de sintetizar y degradar la matriz extracelular en la que se encuentran inmersos. Esta última compuesta de agua, fibras de colágeno y por una red de proteínas (proteoglicanos) altamente anisotrópica, lo que le proporciona su comportamiento característico en respuesta mecánica, demostrado por experimentos de laboratorio [15].
El colágeno encontrado en el cartílago es la misma fibra de proteína insoluble encontrada en los huesos pero con una forma un poco diferente. Cuando el cartílago es sometido a una carga, a través de las fibras de colágeno se presenta el fenómeno de exudación. Las investigaciones sobre la actividad del colágeno en las funciones biomecánicas ha demostrado cada vez más que la integridad de la red de colágeno contribuye de manera importante a las propiedades mecánicas y tribológicas del cartílago [16].
Cualquiera que sea la causa del inicio, el deterioro del cartílago está influenciado por el régimen de carga aplicado durante las actividades cotidianas. Lo anterior conduce a la necesidad de practicar cirugías para la recuperación de la funcionalidad y mejorar la calidad de vida del paciente [17][18][19].
Los criterios de daño para el cartílago articular requieren del uso de modelos constitutivos que sean capaces de describir la naturaleza compleja del comportamiento de este tejido, y determinen con suficiente exactitud los campos de esfuerzo y deformación. Los estudios para evaluar el daño del cartílago corresponden en su mayoría a simulaciones de carga de impacto utilizando el método de los elementos finitos. En estos estudios se contrastan las ubicaciones de iniciación de grietas con las zonas donde aparecen los máximos valores de esfuerzo y deformación. Son varios los criterios de falla que se emplean, siendo los más utilizados el de esfuerzo tangencial máximo, el de esfuerzo normal máximo y el de deformación principal máxima [20].Otro trabajo reciente que muestra un modelo orientado a daño del cartílago es el de Landinez, Garzón y Vanegas [21], donde se presenta un modelo matemático fenomenológico que permite cuantificar el riesgo de falla del cartílago articular por daño acumulativo producto a fatiga. El mismo se basa en el modelo de daño a fatiga para metales, e integra una gran cantidad de información clínica. Los autores plantean que este modelo es adecuado para el estudio y prescripción médica de pacientes, en riesgo de padecer osteoartritis, y para personas que entrenan o realizan deportes.
El presente artículo muestra una revisión sobre los modelos constitutivos de uso más extendido empleados para cartílago articular basados en respuesta mecánica. Se presenta el aparato matemático principal y se realiza un análisis crítico centrado en las características que logra emular satisfactoriamente, sus ventajas y desventajas. Los modelos para cartílago articular que se desarrollen en el futuro probablemente se centren en explicar el comportamiento aislado y cooperativo entre los distintos constituyentes mediante multifases, y de esta forma emular mejor las propiedades altamente anisotrópicas y los comportamientos viscoporoelásticos, de exudación y de inflamación. Los métodos y técnicas experimentales también deberán perfeccionarse para superar las dificultades de obtención de información encontradas hasta el momento.
2. MODELOS CONSTITUTIVOS PARA CARTÍLAGO ARTICULAR
El comportamiento mecánico del cartílago articular ha tratado de ser explicado por medio de la teoría del continuo aplicada a la obtención de modelos reológicos [22][23][24]. El estudio de los fenómenos degradativos del cartílago resulta ser uno de los propósitos más importante para estos modelos. Moskowitz et al. [25] plantea la hipótesis de que la degradación por osteoartritis del cartílago articular es inicialmente causada por carga mecánica. El contacto y la falla del cartílago articular ha sido estudiado tanto experimental como teóricamente [26][9][27], pero existe solo un acuerdo parcial entre las fallas observadas y las regiones predichas de esfuerzos pico.
Se han realizado mediciones experimentales de esfuerzo en la superficie articular para probar varias de las hipótesis de falla formuladas, como lo son las aplicables a los materiales elásticos, en el caso particular para la fase sólida; pero desafortunadamente no todos los componentes de esfuerzos pueden ser medidos y tampoco todas las fallas observadas se encuentran en la superficie. La única vía hasta ahora para obtener una descripción completa de las variaciones de los esfuerzos, espacial y temporal a través de todo el espesor del cartílago, es por solución numérica de modelos matemáticos del cartílago articular. Por su parte, los resultados experimentales indican que el cartílago exhibe visco elasticidad flujo-dependiente, anisotropía y tensión-compresión no lineal debido a su ultra-estructura y composición.
A la fecha, muchos modelos de cartílago articular han sido propuestos para describir su desempeño mecánico. Sin embargo, ninguno de estos ha emulado el espectro completo de respuesta del tejido. Típicamente, cada uno de los modelos propuestos implementa un subconjunto de comportamientos conocidos del tejido, para los cuales las propiedades del material necesitan ser determinadas mediante experimentos.
El cartílago presenta un comportamiento visco-elástico dado por su naturaleza hidratada y su permeabilidad característica. Al tratar de explicar lo anterior, una gran parte de los modelos constitutivos planteados para el cartílago articular se fundamentan en la teoría de Mow [28], quien la adoptó de la mecánica de suelos para tejidos biológicos, y considera al cartílago como un material bifásico. Existen modelos matemáticos que explican la constitución de tejidos fibrosos como el cartílago teniendo en cuenta las características de las fibras de colágeno [29], y se han propuesto muchos modelos constitutivos para el cartílago articular que describen el comportamiento mecánico bajo solicitaciones de cargas simples, como tracción y compresión para condición confinada o libre.
A continuación se presentan un conjunto de modelos constitutivos de importancia para el estudio del cartílago articular, tanto desde la perspectiva histórica como por sus aportes al Estado del Arte.
2.1. Modelo Bifásico de Mow
Este modelo considera al cartílago como un material bifásico compuesto por una fase sólida y una líquida, cada una en si misma incompresible (poro elástico) [28]. El modelo matemático supone que un punto espacial está simultáneamente ocupado por cada una de las fases constituyentes y define cuatro densidades (dos reales y dos aparentes) para el planteamiento de la conservación de la masa. Así mismo, plantea el balance de momento, para las dos fases y para el compuesto globalmente, utilizando una función de la profundidad para los porcentajes de volumen de fase fluida versus fase sólida. Además, utiliza la teoría de mezcla de Crane, Green y Naghdi, así como la reformulación de la ecuación de conservación de masa para mezclas binarias. Considerando una fase sólida lineal elástica con propiedades viscosas y un fluido viscoso incompresible. Se parte del balance de masa para cada una de estas fases,

Donde los superíndices s y f corresponden a la fase sólida y fluida respectivamente.
Adicional al balance de masa se realiza el balance de momentum para cada una de las fases y para el compuesto como un global. También, se utiliza un balance de energía y la desigualdad de la entropía, asumiendo que todos los componentes tienen la misma temperatura,
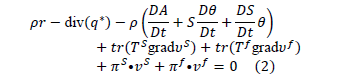
Donde A es la función de energía libre de Helmholtz, S entropía, q temperatura, 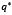 flujo de calor del compuesto y T es el tensor de esfuerzos. El modelo fue validado por sus autores con experimentos de creep y relajación de esfuerzos, característicos de la viscoelasticidad [24].
flujo de calor del compuesto y T es el tensor de esfuerzos. El modelo fue validado por sus autores con experimentos de creep y relajación de esfuerzos, característicos de la viscoelasticidad [24].
Los resultados del modelo de Mow son ampliamente explicados en su trabajo de 1980 [28], donde se realizan experimentos de creep y relajación de esfuerzos en compresión confinada in vitro en cartílago bovino. Las velocidades del fluido intersticial y de la fase sólida calculadas teóricamente demuestran la velocidad relativa como una función de la profundidad durante las fases de compresión y relajación. La tasa de exudación del tejido durante la fase compresiva es constante, consecuentemente con la incompresibilidad intrínseca de las fases del modelo. Mow deja como discusión la dificultad de la obtención de la compresión confinada real, debido al problema de obtener las muestras como cilindros perfectos y sin fricción entre ellas y la cámara. Y también menciona que Hori y Mockros confirman que en la compresión confinada se produce una no linealidad inicial, mientras el espécimen se expande lateralmente y se ajusta a las paredes de la cámara de confinación. Los autores han utilizado este modelo para casos específicos de cartílago [18] y casos específicos de carga [31][32]. Suh y colaboradores, han implementado modelos de elementos finitos bifásicos de penalización para tejidos suaves [33], que también han sido utilizados para comparar con resultados experimentales en cartílago bovino [34].
2.2. Modelo bifásico transversalmente isotrópico
El modelo de elementos finitos planteado por Almeida y Spilker [35], se basa en la descripción de continuo bifásico presentado por Mow [28]. A la fase sólida se le da la característica de isotropía transversal donde la variación de propiedades se define en función de la profundidad, teniendo propiedades iguales en todas las direcciones pertenecientes a cualquier plano perpendicular al vector de profundidad. El modelo es implementado para analizar el contacto articular, siendo empleadas las condiciones de frontera de contacto para interfaces entre diferentes materiales bifásicos desarrolladas por Hou et al. [36].
Se presentan dos hipótesis de soporte para el modelo de isotropía transversal sobre el modelo isotrópico, primero que puede predecir picos de esfuerzo en las zonas de contacto y segundo que los patrones de picos de esfuerzo dependen de la curvatura de las superficies de contacto; lo cual no es cierto en el modelo isotrópico, el cual solo predice picos de esfuerzos únicamente en la interface cartílago-hueso.
Como desventajas, Bursac et al. [37] por medio de experimentos confinados y no confinados, mostró que el modelo de isotropía transversal no es capaz de ajustar simultáneamente los esfuerzos radiales en pruebas confinadas y los altos picos de fuerza axial en las pruebas no confinadas [38]. DiSilvestro et al.[39], y DiSilvestro y Suh [40] mostraron que las curvas de fuerza axial y de desplazamiento lateral no pueden ser simultáneamente ajustadas por el modelo de isotropía transversal.
2.3. Modelo constitutivo para tejido fibroso considerando fibras de colágeno onduladas
Este modelo a diferencia de los dos anteriores introduce por separado la influencia de las fibras de colágeno, considerando una morfología ondulada aleatoriamente de las fibras individuales de colágeno y la relación de esta morfología con la respuesta mecánica del tejido [29][41]. Básicamente se postula que las fibras son rizadas y que tienen diferentes longitudes, así que para una deformación macroscópica éstas serían deformadas en forma diferente y que la respuesta del tejido debe ser entonces no lineal.
El modelo plantea una función de comportamiento de esfuerzo-deformación para una fibra individual. Para un sistema de referencia (X, Y, Z) la fibra tiene un comportamiento de la misma forma para los ejes Y y Z, como variables aleatorias con una distribución normal y media cero,
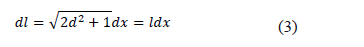
Donde l es una variable aleatoria de densidad de probabilidad dada por P y media 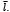 Estos dos últimos parámetros dependen únicamente de
Estos dos últimos parámetros dependen únicamente de 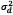 , cuyo valor puede ser medido mediante imágenes médicas.
, cuyo valor puede ser medido mediante imágenes médicas. 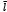 es la longitud de la fibra a partir de la cual ésta empieza a experimentar esfuerzo, el cual está dado por,
es la longitud de la fibra a partir de la cual ésta empieza a experimentar esfuerzo, el cual está dado por,
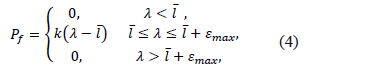
Donde 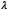 es la deformación de la fibra,
es la deformación de la fibra, 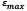 es la deformación máxima de la fibra antes de la falla después del desdoblamiento
es la deformación máxima de la fibra antes de la falla después del desdoblamiento 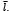
Se pueden distinguir dos casos en el modelo en los que el tejido es sometido a carga en la dirección de las fibras (ver Figura 1). En el primer caso, las fibras son gradualmente cargadas a medida que el tejido es deformado. En un punto todas las fibras ya han sido estiradas y la resistencia debido a las fibras es constante. Por tanto, la carga es soportada por una fase elástica hasta la falla. En el segundo caso, algunas fibras empiezan a fallar porque han llegado a su deformación máxima mientras otras no han sido totalmente estiradas.
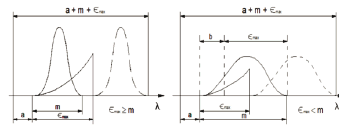
Figura 1. Esquema de deformación de fibra de colágeno. Adaptada de [29]
El modelo introduce una no linealidad característica del cartílago que no es capaz de describir los dos modelos anteriores. Otro aporte es que correlaciona la morfología fibrosa del cartílago articular con su respuesta mecánica, empleando una distribución aleatoria, que caracteriza a las fibras, medida por medio experimental.
2.4. Modelo bifásico no lineal visco-hiperelástico
El modelo, de García y Cortés [42], está formulado en elementos finitos, es un modelo no lineal visco-porohiperelástico, el cual considera deformaciones finitas, permeabilidad no lineal y una fase sólida hiperelástica. Suma los efectos viscosos intrínsecos de la matriz de proteoglicanos y utiliza una ecuación constitutiva no lineal hiperelástica [43]. La ecuación propuesta satisface un modelo de carga uniaxial de tipo sólido viscoso en el cual la acción de los resortes es representado por la función hiperelástica propuesta por Holmes y Mow [31]. El cartílago es considerado un material bifásico isotrópico, y para la solución es utilizada la formulación de sólido mixta de velocidad y presión en los poros usando un esquema Lagrangiano actualizado.
La función hiperelástica propuesta por Holmes y Mow es considerada para describir la deformación de equilibrio cuando la presión de poro es nula, y los efectos viscosos de la fase sólida han sido disipados,
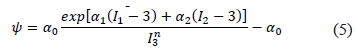
Donde 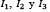 son los invariantes del tensor de deformaciones de Green B; mientras
son los invariantes del tensor de deformaciones de Green B; mientras 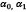 ,
, 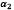 y n son coeficientes elásticos, los cuales satisfacen la siguiente condición
y n son coeficientes elásticos, los cuales satisfacen la siguiente condición 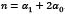 . De la ecuación de hiperelasticidad se encuentra que la relación entre el tensor de Cauchy y el de Green está dada por,
. De la ecuación de hiperelasticidad se encuentra que la relación entre el tensor de Cauchy y el de Green está dada por,
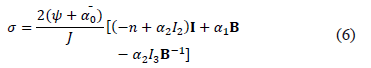
Donde J es el determinante del tensor gradiente de deformación F, e I es la matriz identidad. Para la respuesta transitoria de la fase sólida es usada la ecuación propuesta por Belytschko, Liu y Moran [44], que está en términos del segundo tensor de esfuerzos de Piola S y el tensor de deformaciones de Lagrange E. De lo anterior se obtiene la ecuación constitutiva de la fase sólida del modelo (7). En la Figura 2 se representa el esquema que explica este modelo [42].
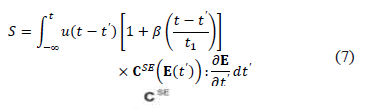
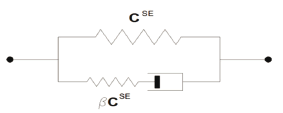
Figura 2. Diagrama para el modelo bifásico no lineal visco-hiperelástico. Adaptada de [42]
La ecuación constitutiva ha sido implementada en un algoritmo Lagrangiano no lineal. La misma está basada en la formulación de sólido mixta de velocidad y presión de poros obtenida por Almeida y Spilker [45] utilizando elementos de cuatro nodos. El modelo puede ser usado para representar el comportamiento mecánico de la matriz de proteoglicanos con matriz reforzada. García y Cortés [42] reportan en general un buen ajuste de los resultados del modelo con las curvas experimentales que aparecen en la literatura; aunque algunos valores de coeficientes de correlación no son muy altos, y se presentan algunos problemas de convergencia para niveles de deformación por encima de 40%. Por otro lado, sugieren que la ecuación obtenida puede ser incorporada a un modelo fibro-reforzado que permita considerar la anisotropía, no homogeneidad y la no linealidad tensión-comprensión; y así representar de mejor manera el comportamiento microestructural del cartílago y lograr un mejor ajuste con las curvas experimentales.
También se han implementado modelos viscohiperelásticos para el comportamiento de los ligamentos [46]. Este modelo puede describir deformaciones finitas gracias a la introducción de la función hiperelástica de la fase sólida.
2.5. Modelo bifásico visco-hiperelástico fibro-reforzado para cartílago articular
García y Cortés [38] introducen en su modelo anterior la característica fibroreforzada de cartílago. Siendo este modelo capaz de describir la viscoelasticidad intrínseca de los componentes fibrilares y no fibrilares de la fase sólida del cartílago, y la respuesta no lineal de esfuerzo-deformación bajo tracción y compresión. A este modelo se le incorpora la propiedad viscoelástica de las fibras de refuerzo por medio de una función de visco hiperelasticidad similar a la usada para la matriz. La forma diferencial de la ley viscohiperelástica es,
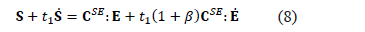
Donde S es el segundo tensor de esfuerzos de Piola, E es el tensor de deformación de Lagrange, 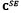 es el segundo tensor de elasticidad,
es el segundo tensor de elasticidad, 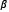 y
y 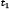 son parámetros del modelo, y el punto indica la derivada material. En la Figura 3 se muestra el modelo uniaxial para deformaciones infinitesimales. Como se puede observar el parámetro
son parámetros del modelo, y el punto indica la derivada material. En la Figura 3 se muestra el modelo uniaxial para deformaciones infinitesimales. Como se puede observar el parámetro 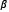 brinda la información de comportamiento viscoelástico del modelo.
brinda la información de comportamiento viscoelástico del modelo.
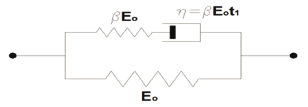
Figura 3. Diagrama para el modelo bifásico visco-hiperelástico fibro-reforzado. Adaptada de [38]
La función hiperelástica utilizada para las fibras es la propuesta por Limbert y Middleton [47],
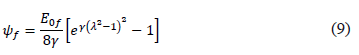
Donde 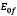 es el módulo de Young para deformación cero,
es el módulo de Young para deformación cero, 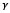 es usado para ajustar las curvas de esfuerzo-deformación y
es usado para ajustar las curvas de esfuerzo-deformación y  es la relación de estricción. En el modelo, el esfuerzo de equilibrio de Cauchy es calculado para las fibras como,
es la relación de estricción. En el modelo, el esfuerzo de equilibrio de Cauchy es calculado para las fibras como,
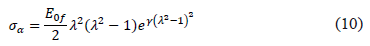
La ley constitutiva ha sido implementada en un algoritmo Lagrangiano actualizado basado en la formulación de sólido mixta de velocidad-sólido y presión de poros, realizada por Almeida y Spilker [45], usando elementos cuadriláteros axisimétricos (4 nodos). Los resultados numéricos han sido validados con la solución cerrada obtenida por la transformación de Laplace y el correspondiente principio de viscoelasticidad. El modelo es capaz de considerar simultáneamente la respuesta no lineal de tracción-compresión, los efectos de la viscoelasticidad intrínseca de los dos componentes de la fase sólida y la no linealidad de las curvas esfuerzo-deformación para deformaciones finitas.
En la revisión de otros modelos visco elásticos fibro-reforzados se encuentra que los de Wilson et al. [48] y Li et al. [49] presentan la posibilidad de describir las curvas de equilibrio esfuerzo – deformación, bajo tensión y compresión, y la opción de incluir los efectos viscosos intrínsecos de la matriz de proteoglicanos y las fibras de colágeno. Estos modelos pueden ser ajustados por medio de los parámetros elásticos de las funciones hiperelásticas y los dos parámetros viscosos, para el tiempo y porcentaje de relajación presentes en cada fase sólida.
DiSilvestro et al. [39] y DiSilvestro and Suh [40] mostraron que las curvas de fuerza axial y del desplazamiento lateral pueden ser simultáneamente ajustadas al incluir la viscosidad intrínseca de la fase sólida, lo que da esa ventaja al modelo por incluir tal consideración. Por su parte, Li y colaboradores hacen una revisión de modelos poroelásticos fibroreforzados utilizados para el comportamiento mecánico del cartílago articular [50].
2.6. Modelo poroviscoelástico fibroreforzado emulador de la dilatación
El elemento de mayor influencia en el comportamiento mecánico del cartílago articular es su ajustada ultraestructura, formada por la red de colágeno y los proteoglicanos. Como consecuencia las cargas dentro del tejido provocan una diferencia de presión entre el exterior y el interior haciendo que este se inflame (Urban et al. [51]). Varios modelos incluyen el fenómeno de dilatación del cartílago por medio de la inclusión de una tercera fase. De manera que se tiene: una fase sólida incompresible, una fase fluida y una fase iónica. El modelo utiliza la hipótesis de que si se incluyen las propiedades de dilatación debido a los cambios en la densidad de proteoglicanos y las características visco-elásticas de la red de colágeno, se pueden explicar tanto las pruebas de compresión confinada y no confinada, así como la indentación y el fenómeno de dilatación [52]. La fase sólida consiste en una parte que se puede inflamar, no fibrilar que representa la matriz, la cual contiene mucho proteoglicanos, y una parte fibrilar que representa la red de colágeno. Ambas partes son incluidas en un elemento continuo. Se asumen unas fibras primarias y unas secundarias para la red de colágeno como en la propuesta por Wilson et al. [48]. En la Figura 4 se muestra un modelo de arco para las fibras de colágeno en el que la dirección es perpendicular a partir del hueso subcondral. Estas últimas toman un radio hasta la superficie y las fibras secundarias tienen una dirección aleatoria
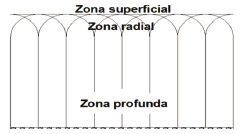
Figura 4. Orientación de las fibras primarias como función de la profundidad. Adaptada de [52]
El comportamiento viscoelástico de las fibras es representado por un resorte lineal, paralelo a uno no lineal en serie con un amortiguador (modelo de viscoelasticidad estándar) [52]. Asumiendo que las fibras solo soportan tensión se tiene la siguiente expresión,
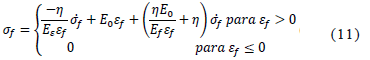
Donde 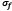 y
y 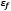 son el esfuerzo y la deformación de las fibras respectivamente. La ecuación ha sido obtenida por medio de un esquema implícito regresivo de Euler, donde se tienen en cuenta la densidad de las fibras dependiendo de la profundidad, y la cantidad relativa de fibras primarias y fibras secundarias.
son el esfuerzo y la deformación de las fibras respectivamente. La ecuación ha sido obtenida por medio de un esquema implícito regresivo de Euler, donde se tienen en cuenta la densidad de las fibras dependiendo de la profundidad, y la cantidad relativa de fibras primarias y fibras secundarias.
Los esfuerzos en las fibras primarias y secundarias respectivamente son,
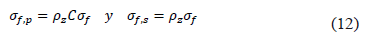
Donde 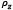 es un factor que toma en cuenta la densidad de las fibras como función de la profundidad y C es la cantidad de fibras primarias con respecto a las fibras secundarias. Para el comportamiento de la matriz sólida no fibrilar el modelo emplea un comportamiento compresible Neo-Hookean,
es un factor que toma en cuenta la densidad de las fibras como función de la profundidad y C es la cantidad de fibras primarias con respecto a las fibras secundarias. Para el comportamiento de la matriz sólida no fibrilar el modelo emplea un comportamiento compresible Neo-Hookean,
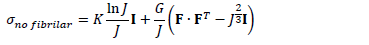
Donde J es el determinante del tensor gradiente de deformación F, mientras K y G son funciones de las propiedades elásticas del material.
Obviamente los modelos que no incluyen el fenómeno de dilatación (inflamación) del cartílago, no pueden explicar las pruebas experimentales centradas en este comportamiento. Esta dilatación implica cambios en las curvas de relajación, los cuales no pueden ser descritos por ninguno de los modelos anteriores. Otra fortaleza del modelo es que puede describir simultánea y apropiadamente la compresión confinada y no confinada, dilatación e indentación, utilizando para todas estas pruebas un conjunto simple de parámetros. Además, los autores consideran que este modelo puede ser usado para el estudio de la fisiología y la patología del cartílago, siendo idóneo para una mejor comprensión de los mecanismos de daño del cartílago articular.
Es necesario anotar que también se han utilizado modelos que tienen en cuenta la dilatación para estudiar el comportamiento de arterias [53].
2.7. Modelos químico-mecánicos
Se han desarrollado modelos en los que se incluyen los fenómenos químicos-mecánicos para explicar las distintas respuestas del cartílago bajo las solicitaciones fisiológicas [54][55]. Como es el caso del modelo planteado por Loix, Simoes y Loret [55], que consiste en un planteamiento electro-químico-mecánico trifásico multiespecie, el cual tiene en cuenta los compuestos de la matriz del colágeno y las características electroquímicas de la red de proteoglicanos. Por tanto, se consideran sus interacciones de manera mecánica y química, teniendo en cuenta también los efectos de remplazos iónicos en las cargas de los compuestos que componen el cartílago.
3. CONCLUSIONES
El modelado del cartílago articular con resultados que emulen sus características y comportamiento debe ser realizado empleando al menos un modelo bifásico, ya que debido a la complejidad estructural y de comportamiento del tejido, un modelo más simple sesgaría la explicación de los fenómenos viscoelásticos que se presentan en el cartílago como la rehidratación y la exudación. El modelo de Mow y colaboradores [28] con su teoría bifásica marcó un hito en el estudio teórico del cartílago articular, ya que la mayoría de los modelos posteriores retoman dichos planteamientos. Sin embargo, la inclusión de la viscoelasticidad intrínseca en la fase sólida mejora la aproximación al comportamiento explicado sin dicha consideración. Una mejor aproximación del comportamiento real del cartílago se da con la inclusión del fibrorefuerzo por separado. El planteamiento de un modelo fenomenológico para el cartílago articular posee un grado de complejidad alto debido a la naturaleza de la respuesta bajo cargas transitorias y a los fenómenos físico químicos acoplados que tienen lugar. Los modelos futuros deberán estar orientados a considerar integralmente dichas características e interacciones.
REFERENCIAS
[1] Knecht, S., Vanwanseele, B. and Stussi, E., A review on the mechanical quality of articular cartilage – Implications for the diagnosis of osteoarthritis, Clinical Biomechanics, 21, pp. 999-1012, 2006. [ Links ]
[2] Insall, J., Windsor, R., Scott, W., Kelly, M. and Aglietti, P., Cirugía de la Rodilla. Editorial Médica Panamericana S.A, Buenos Aires, Argentina, 1994. [ Links ]
[3] Fanjul, J. M., Artroplastia Total De La Cadera Primaria: Optimización de resultados en función del acto médico, Oviedo, España, 2004. Available: http://www.ovenet.com/fanjul/ [citado: 20 de Noviembre de 2004]. [ Links ]
[4] Kaddick, C., Wimmer, M.A., Hip simulator wear testing according to the newly introduced standard ISO 14242, Eng. Med., 215, pp. 229-242, 2001. [ Links ]
[5] Smith, S.L., Burgess, I.C., Unsworth, A., Validation of a hip joint wear simulator, En: British Orthopedic Research Society Meeting, Sheffield, UK, March, 1997. [ Links ]
[6] Goldsmith, A., Dowson, D., Development of a ten-station, multi-axis hip joint simulator, Eng. Med, pp. 213, 311-316, 1999. [ Links ]
[7] Pyburn, E., Goswami, T., Finite element analysis of femoral components paper III: Hip joints, Material and Design, 25, pp. 705-713, 2004. [ Links ]
[8] Scifert, C., Brown, T. and Lipman, J.D., Finite element analysis of a novel design approach to resisting total hip dislocation, Clinical Biomechanics, 14, pp. 697-703, 1999. [ Links ]
[9] Moreo, P., Garcia-Aznar, J. and Doblare, M., A coupled viscoplastic rate-dependent damage model for the simulation of fatigue failure of cement–bone interfaces, International Journal of Plasticity, 23, pp. 2058-2084, 2007. [ Links ]
[10] Paul, J.P., Force actions transmitted by joints in the human body. Proc. Inst. Mech. Eng, 1976. [ Links ]
[11] Harrison, Principios de Medicina Interna. España. McGraw Hill - Interamericana de España, 1994. [ Links ]
[12] Nordin, M., Frankel, V., Biomecánica básica del sistema músculo-esquelético. McGraw Hill Interamericana, España, 2004. [ Links ]
[13] Vidal A., Arroyo, R., Análisis y simulación del desgaste de cartílago de articulación de rodilla, Vocacionamiento Ciencia y Tecnología, 13, 10, 2006. [ Links ]
[14] Tónnis, D., Congenital dysplasia and dislocation of the hip. Springer Verlag, Berlin, Alemania, 1994. [ Links ]
[15] Huang, C.Y., Stankiewicz, A., Ateshian, G. and Mow, V. C., Anisotropy, inhomogeneity, and tension-compression nonlinearity of human glenohumeral cartilage in finite deformation. Journal of biomechanics, 38, pp. 799-809. 2005. [ Links ]
[16] Katta, J., JIN, Z. and Ingham, E., Biotribology of articular cartilage -A review of the recent advances, Med Eng Phys, pp. 1349-1363, 2008. [ Links ]
[17] Arango, A., Prótesis de cadera menos radicales. Available: http://www.saludpanama.com/protesis-de-cadera-menos-radicales. [Citado: 2006]. [ Links ]
[18] Pastrana, F., Lopez, A., Carrillo, F. and Zapata, R., Artroplastia de interposición con mínima resección ósea en el tratamiento de la artrosis postraumática del codo, Rev Mex Ortop Traum, 13, pp. 331- 334, 1999. [ Links ]
[19] Mont, M.A., Ragland, P.S., Etienne, G. and Seyler, T.M., Hip resurfacing arthroplasty. J Am Acad Orthop Surg. 14:454-63, 2006. [ Links ]
[20] Wilson, W., Van Donkelaar, C.C., Van Rietbergen, R. and Huiskes, R., The role of computational models in the search for the mechanical behavior and damage mechanisms of articular cartilage, Medical Engineering & Physics, 27, pp. 810–826, 2005. [ Links ]
[21] Landinez-Parra, N.S., Garzón-Alvarado, D.A. and Vanegas-Acosta, J.C., A phenomenological mathematical model of the articular cartilage damage, computer methods and programs in biomedicine, 104, pp. 58–74, 2011. [ Links ]
[22] Landinez, N., Vanegas, J. and Garzón, D., Modelado matemático del comportamiento mecánico de un fragmento de cartílago articular, Revista Dyna, 157, 76, pp. 133 - 144, 2009. [ Links ]
[23] SHABANA, Computational Continuum Mechanics. Cambridge Univerity Press, 2008. [ Links ]
[24] Mase, G.T. and Mase, G.E., Continuum Mechanics for Engineers. Ed. CRC Press LLC, United States of America, 1999. [ Links ]
[25] Moskowitz, R. W., Experimental models of osteoarthritis, in Diagnosis and medical/surgical management, 2nd ed. Ed. Lippincott Williams & Wilkins, 1992. [ Links ]
[26] Geris, L., Gerisch, A., Maes, C., Carmeliet, G., Weiner, R., Vander, J. and Oosterwyck, V., Mathematical modeling of fracture healing in mice: comparison between experimental data and numerical simulation results, Med Biol Eng Comput, 44, pp. 280-289, 2006. [ Links ]
[27] Peña, E., Calvo, B., Martínez, M.A. and Doblaré, M., Computer simulation of damage on distal femoral articular cartilage after meniscectomies, Computers in Biology and Medicine, 38, pp. 69-81, 2007. [ Links ]
[28] Mow, V.C., Kuei, S., Lai, W.M. and Armstrong, C.G., Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments, Journal of Biomechanical Engineering, 102, pp. 73-84, 1980. [ Links ]
[29] Cacho, F., Elbischger, P.J., Rodriguez, J., Doblaré, M. and Holzapfel, G., A constitutive model for fibrous tissues considering collagen fiber crimp, International Journal of Non-Linear Mechanics, 42, pp. 391-402, 2007. [ Links ]
[30] Donzelli, V., Spilker, R., Ateshian, G. and Mow, V.C., Contact analysis of biphasic transversely isotropic cartilage layers and correlations with tissue failure, Journal of Biomechanics, vol. 32, pp. 1037-1047, 1999. [ Links ]
[31] Holmes, M. H. and Mow, V. C., The non-linear characteristics of soft gels and hydrated connective tissues in ultrafiltration, Journal of Biomechanics, 23, pp. 1145-1156, 1990. [ Links ]
[32] Kwan, M., Lai, M., and Mow, V. C., A finite deformation theory for cartilage and other soft hydrated connective tissues - I. Equilibrium results, J. Biomechanics, 23, pp. 145-155, 1990. [ Links ]
[33] Suh, J., Spilker, R. and Holmes, M., A penalty finite element analysis for non-linear mechanics of biphasic hydrated soft tissue under large deformation, International Journal of Numerical Method in Engineering, 32, pp. 1411-1439, 1991. [ Links ]
[34] Athesian, G., Warden, W., Kim, J., Grelsamer. and Mow, V., Finite Deformation Biphasic Material Properties of Bovine Articular Cartilage from Confined compression experiments, J. Biomechanics, 30, pp. 1157-1164, 1997. [ Links ]
[35] Almeida, E. and Spilker, R., Finite element formulations for hyperelastic transversely isotropic biphasic soft tissues, Comput. Methods Appl. Mech. Engrg, 151, pp. 513- 538, 1998. [ Links ]
[36] Hou, J.S., Holmes, M.H., Lai, W.M. and Mow, V.C., Boundary conditions at the cartilage-synovial fluid interface for joint lubrication and theoretical verifications, Journal of Biomechanical Engineering, 111, pp. 78-87, 1989. [ Links ]
[37] Bursac, P.M., Obitz, T.W., Eisenberg, S.R. AND Stamenovic, D., Confined and unconfined stress relaxation of cartilage: appropriateness of a transversely isotropic analysis, Journal of Biomechanics, 32, pp. 1125–1130, 1999. [ Links ]
[38] García, J.J. and Cortés, D. H., A biphasic viscohyperelastic fibril-reinforced model for articular cartilage: Formulation and comparison with experimental data, Journal of Biomechanics, 40, pp. 1737-1744, 2007. [ Links ]
[39] Disilvestro, M., Wong, M., Jurvelin, J.S. and Zhu. Q., Biphasic poroviscoelastic simulation of the unconfined compression of articular cartilage: I-Simultaneous prediction of reaction force and lateral displacements. Journal of Biomechanical Engineering, 39, pp. 2991–2998, 2001. [ Links ]
[40] Disilvestro, M. R. and Suh, J. K., A cross-validation of the biphasic poroviscoelastic model of articular cartilage in unconfined compression, indentation, and confined compression, Journal of Biomechanics, 34, pp. 519-525, 2001. [ Links ]
[41] Cacho, F., Constitutive models for fiber-reinforced soft biological tissues, Zaragoza, España, 2006. [ Links ]
[42] García J.J. and Cortés, D.H., A nonlinear biphasic viscohyperelastic model for articular cartilage, Journal of Biomechanics, 39, (16) pp. 2991-2998, 2006. [ Links ]
[43] García, J.J. and Cortés, D.H., Modelo bifásico no-lineal de elementos finitos para el análisis mecánico de tejidos biológicos. Parte I, Ingeniería y Desarrollo, Universidad del Norte, 19, pp. 57-73, 2006. [ Links ]
[44] Belytschko, T., Liu, W. and Moran, B., Non linear Finite Elements for Continua and Structures, Wiley, Chichester, 2000. [ Links ]
[45] Almeida, E., Spilker, R., Element, mixed and penalty finite models for the nonlinear behavior of biphasic soft tissues in methods, deformation: part I - alternate formulations, Computer Methods in Biomechanics and Biomedical Engineering, 1, pp. 25–46, 1997. [ Links ]
[46] Peña, E., Calvo, B., Martínez, M.A. and Doblaré, M., An anisotropic visco-hyperelastic model for ligaments at finite strains. Formulation and computational aspects, International Journal of Solids and Structures, 44, pp. 760-778, 2007. [ Links ]
[47] Limbert, G. and Middleton, J., A transversely isotropic viscohyperelastic material, International Journal of Solids and Structures, 41, pp. 4237-4260, 2004. [ Links ]
[48] Wilson, W., Van Rietbergen, B., Ito, K. and Van Donkellar, C., Stresses in the local collagen network of articular cartilage: a poroviscoelastic fibril-reinforced finite element study, Journal of Biomechanics, 37, pp. 357–366, 2004. [ Links ]
[49] Li, L.P., Herzog, W., Korhonen, R.K. and Jurvelin, J.S., The role of viscoelasticity of collagen fibers in articular cartilage: axial tension versus compression, Medical Engineering and Physics, 27, pp. 51-57, 2005. [ Links ]
[50] Li, L., Shirazi-Adl, A. and Buschmann, M., Investigation of mechanical behavior of articular cartilage by fibril reinforced poroelastic models, Biorheology, 40, pp. 227-233, 2003. [ Links ]
[51] Urban, J., Maroudas, A., Bayliss, M. and Dillion, J., Swelling pressure of proteoglycans at the concentration found in cartilaginous tissues, Biorheology, 16, pp. 447-464, 1979. [ Links ]
[52] Wilson, W., Van Donkelaar, C.C., Van Rietbergen, B. and Huiskes, R., A fibril-reinforced poroviscoelastic swelling model for articular cartilage, Journal of Biomechanics, 38, pp. 1195- 1204, 2005. [ Links ]
[53] Simon, B., Kaufman, M., Liu, J. and Baldwins, A., Porohyperelastic-transport-swelling theory, material properties and finite element models for large arteries, Int. J. Solids Structures, 35, pp. 5021-5031, 1998. [ Links ]
[54] Loret, B. and Simoes, F., Articular cartilage with intra - and extrafibrillar waters: a chemo-mechanical model, Mechanics of Material, 515 & 541, pp. 515-541, 2004. [ Links ]
[55] Loix, F., Simoes, F. and Loret, B., Articular cartilage with intra and extrafibrillar waters – Simulations of mechanical and chemical loadings by the finite element method, Computer Methods in Applied Mechanics and Engineering, 197, pp. 4840-4857, 2008. [ Links ]














