Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
DYNA
versión impresa ISSN 0012-7353versión On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.79 n.173 Medellín mayo/jun. 2012
AGENT-BASED SIMULATION APPROACH TO URBAN DYNAMICS MODELING
APROXIMACIÓN AL MODELAMIENTO DE DINÁMICAS URBANAS A PARTIR DE SIMULACIÓN BASADA EN AGENTES
FEDERICO LIÉVANO MARTÍNEZ
M.Sc, Universidad Rovira i Virgili, Spain, fedeingen@gmail.com
YRIS OLAYA MORALES
Ph.D. Universidad Nacional de Colombia, yolayam@unal.edu.co
Received for review: August 05th, 2011, accepted: February 06th, 2012, final version: April 10th, 2012
RESUMEN: Este artículo presenta un esquema general de micro-simulación que captura importantes relaciones dinámicas y procesos de toma de decisiones entre agentes que afectan el espacio urbano. El artículo muestra cómo, a partir de formulaciones económicas y de la interacción de agentes, se logran simular patrones globales de comportamiento y dinámicas de ocupación del suelo urbano.
PALABRAS CLAVE: dinámicas urbanas, procesos de toma de decisión, simulación basada en agentes.
ABSTRACT: This article presents a general agent-based simulation approach that captures agents' decision-making processes and dynamic relationships that determine urban shape. The article shows how to simulate urban growth patterns and land-use change dynamics using economic assumptions and by modeling the interactions of computational agents.
KEYWORDS: agent-based simulation, land use change, urban dynamics, decision-making processes.
1. INTRODUCTION
Individual decisions determine changes in land use, but they are also determined by land-use policies and planning. Urban planners need to understand the dynamics of land-use changes in order to assess local policies and devise the economic and regulatory incentives to guide urban growth. However, urban systems are highly complex and involve non-linear interactions of physical, economic, and governmental agents with conflicting interests. Such systems can reach different equilibrium states through a variety of trajectories. As a result, urban dynamics processes are still poorly understood [1].
The models for explaining land-use and land-use changes range from stylized models of economic equilibrium, [2–4] in which spatial features are simplified and decision-makers are highly homogeneous, [5–8] to detailed comprehensive models that integrate economic modeling with spatial data and computer simulation.
Equilibrium models have been extended by adding a spatial dimension and by integrating the interaction between transportation demand and land-use [9,10], and more recently, equilibrium models add endogenous congestion effects [11,12]. Spatial interaction models have also been modified to include dynamic adjustments in production and demand [13].
Forrester [14] takes a different approach and develops a simulation model that directly addresses the complexity of urban dynamics. In Forrester's model, population and economic growth drive urban growth within a fixed land area and the city is a self-regulatory system going through a cycle of growth, maturity, and decline. This model was the first to include both the positive and negative feedback loops of urban systems, thus explaining some unintended results of policies such as housing subsidies.
With the increased availability of geographical information systems and data, urban models are now more disaggregated than the models discussed above. The recent literature on computer models of land-use changes is extensive; see [1] for a comprehensive review. Urban modeling is now approached from complex systems theory. Models for complex systems use behavioral and allocation rules to reproduce emergent behaviors. The most commonly used modeling approaches are cellular automata [15], and agent-based simulation [16].
Agent-based simulation models were first developed during the 1980s [17–20] with a growing number of applications to computer science [21–23] , software development, control systems, [24–26] and negotiation [27]. Applications in complex socio-economic systems are less common, but agent-based simulation models have been applied to study markets and economic systems [28] and they have also been incorporated to wide-scale urban planning models [29].
To our knowledge, with the exception of [30], who develops and tests agent-based models of urban sustainability, there have been no instances of ABS for studying urban dynamics in Colombia. This is partly because agent based simulation (ABS), and its applications are not well known by urban planners. In this paper, we use a model developed by [30] to explain how the ABS methodology can be applied to model dynamics of urban land-use changes. This model is developed using NETLOGO, an open multi-agent modeling environment developed by [31].
This article is organized as follows: Section 2 presents the simulation environment and the main concepts for building an agent-based model. The methodology is illustrated in Section 3, using a model developed by [30]. The model formulation and simulation results are presented in Sections 4 and 5, respectively.
2. MODELING URBAN LAND-USE DYNAMICS USING AGENT-BASED SIMULATION
Agent-based simulation is a technique for modeling processes as dynamic systems of interacting agents. An agent is a software piece containing information, attributes and behavior, and which represents an entity of an artificial computational world [32]. Agent-based modeling is essentially a collection of algorithms logically programmed into the methods of the classes that represent the agents [33]. A class contains information (attributes and variables) and behavior methods that act upon such information. Methods and information can be public, private, or protected-meaning that different computing entities have different access to information [34], and interaction between model's agents arises from information exchanges established in their behavior methods.
In an urban land-use model, an agent can represent an individual (e.g., worker, consumer); a social group (e.g., family, industry, government); an institution (e.g., market, regulation system); a biological entity (e.g., ecosystem, forests); or a physical entity (e.g., infrastructure, regions). Agents can have learning capabilities, similar to the human cognitive functions and abilities [28]. In addition, agents can be organized hierarchically. For example, an agent representing an industry can be composed of agents with a lower hierarchical range, such as a worker or a manager.
Ideally, classes representing agents would have the same decision-making and flexibility of the real world-entities they represent. This means that agents behave according to their preferences, institutions, and constraints; and that no external equilibrium conditions are imposed. Once the classes and methods representing real-world entities are built, the rules and mechanisms governing agent interactions are built. Interaction mechanisms can be face-to-face, neighborhood rules, processes, and laws, among other rules [28].
In addition, an agent-based model can contain artifacts, which are elements that make no decisions, but are part of an agent's environment and can affect an agent's behavior. In an urban model, artifacts can represent natural resources such as rivers or forests, or infrastructure elements [35]. Finally, an ABS model has parameters and auxiliary variables which contain exogenous information about initial conditions, and that can also be used for controlling simulation and changing simulation settings.
From a set of initial conditions, the state of the system is updated during each simulated time step, by applying the behavioral methods and interaction rules, and by updating the agents' information. Such a model is dynamically complete because it updates its state based on the interactions between agents and the initial conditions, with no external intervention.
In the next section, we describe the structure and components of an urban land-use model developed by [30] which was implemented in NETLOGO [31].
2.1. Agent-based modeling in Netlogo
NetLogo is a free and open source modeling environment designed for simulating complex social phenomena. It was authored by Uri [31] and it is being developed by Northwestern University's Center for Connected Learning and Computer-Based Modeling. A complete guide to agent-based simulation using NetLogo can be found in [31]. In this section, we briefly define the main components of the programming environment.
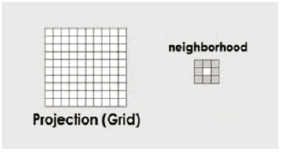
Patches: The NetLogo world is a two-dimensional grid of patches, which are individual squares (or cells) in the grid. These patches are a type of agent that can be used to represent both urban land and its state, and their position is represented by coordinates. The size and number of cells can be adjusted using the settings option in NetLogo's tool bar (See Fig. 1).

Figure 1. Patch setting option in Netlogo From Wilensky (1999)
Agents. Agents are discrete entities which can follow instructions. Each agent carries out its own activity, all simultaneously [31]. There are four types of agents: turtles, patches, links, and the observer. Turtles are agents that can move and can be positioned in any part of a patch. In a land-use model, these agents can be families or industries. As discussed before, patches are agents that do not move, although they have behaviors. A link is an agent connecting two turtles and can be used for modeling relationships such as father/child. Finally, the observer agent does not have a location and it can be used to model institutions, which interact with other agents. Figure 2 depicts a set of specific turtle agents with the ants form.

Figure 2. Example of NetLogo's turtle agents. From Wilensky (1999)
Agent variables. These variables store agents' attributes. Global variables have only one value and can be accessed by every agent. By contrast, variables belonging to each agent have their own value [31].
Procedures. NetLogo provides two types of directions for agents: commands and reports. Commands, such as "move-to", "die", or "clear" control agents' behaviors. Reports are used for asking agents to compute a value and return the result. Basic commands and reporters built into NetLogo are called primitives. User-defined commands and reporters are called procedures. Algorithm 1 shows an example of a procedure for moving agents randomly.
3. AN EXAMPLE OF A MODEL OF URBAN LAND-USE USING NETLOGO
As discussed before, our example is based on a model developed by [30]. This model contains two main sectors: industry and labor. Urban growth responds to economic and population growth and it is constrained by the exhaustion of natural resources; in this case, land. The model components are summarized below:

Algorithm 1. Algorithm for agents' random movement
3.1. Urban land
NetLogo's patches form a grid which, in this case, represents urban land. Urban grid cells have two states: developed or undeveloped. The cells with trees represent undeveloped areas, while colored cells represent developed land. The intensity of a color depends on the value (price) of developed land, which is one of the attributes of land in the model. Other attributes belonging to the cells are: attractiveness, which represents the preferences of agents for occupying a cell; price, which represents the economic value of land; density, which is the number of buildings per area unit; and distance, which is the distance of the nearest work center.
3.2. Agents
There are two main classes of agents: developers and households. Each class is subdivided into types, according to the attributes of the agents. Household agents are a group of persons that demand housing. Households have unique attributes, mainly income and work location. Household agents prefer housing units that are closer to their place of work.
In this model, households are reactive agents and dynamics is driven by the behavior of developers. Developers transform urban land by building housing or industry units. Developers' types are defined based on the sector they attend (low or high income, for example), but all developers perform the same actions that change land use. These actions are: deforesting, changing land value, changing land attractiveness, and increasing density.
Deforestation occurs every time an undeveloped cell is urbanized. Urbanization also implies changing land value because high-value buildings increase neighborhood price whereas low-value buildings decrease the value of a land cell and of neighboring cells. Similarly, urbanization changes the attractiveness of land and the density of its population.
3.3. Artifacts
At the beginning of the simulation, the land is covered by forests which represent rural areas, open spaces, or other environmental amenities which are affected by urban growth. Forests are an artifact which is defined to make a future analysis of urban growth sustainability.
3.4. Parameters, controls, and exogenous variables
Controls are used for initializing agents and cells' attributes as well as for governing the simulation. Parameters and exogenous variables are defined for experimenting under different conditions. Among the parameters that can be changed by users are: initial endowment of forest land, growth rates for a given population, number of jobs created by a particular industrial unit, the number of industrial units that can be built during the simulation, and the average number of persons in each household. Users can also change developers' search parameters and preferences.
In the following section, we describe in greater detail the assumptions used for building the behavioral methods of developer and person agents.
4. MODEL FORMULATION
We assume that agents are rational and that they maximize utility. Developers have complete information about developed and non-developed land, and their utility function ranks available land units according to their attractiveness, location, and building density. As discussed above, persons (corresponding to households) are passive agents in this model, which is consistent with other approaches [36]. An agent demanding housing is assigned to the unit closest to his or her job and with the lowest price. In the case of a tie between housing alternatives, the model assigns a random housing unit to the agent. Population increases each time step, according to an exogenously defined growth rate. This population growth fuels housing demand. Although this is not a model of the housing market, agents compete for the land units that are more accessible, and land units are allocated to the agents that value them most.
4.1. Developers' behavior
As discussed previously, developers maximize a utility function. Developer utility has two components: a deterministic component, represented by a Cobb-Douglas function that represents their preferences, and a random component that reflects uncertainty in decision-making [37]. Although developers have perfect information about land cells, they do not evaluate all undeveloped cells. Instead, they evaluate the utility of developing each land unit belonging to a random sample, which is drawn from the set of all available units, using a uniform probability distribution function.
The utility function of Eq. (1) is a Cobb-Douglas function commonly used in ABS [31,38].
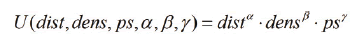
U is the utility of developers, which depends on the distance of the land unit to the nearest commercial or work center, dist; on the density of buildings in the land unit, dens; and on the attractiveness of the land unit for persons, ps. These factors are weighed using parameters  , and
, and  which vary according to the developer's type in order to represent the preference of developers of low-income, high-income, and commercial neighborhoods.
which vary according to the developer's type in order to represent the preference of developers of low-income, high-income, and commercial neighborhoods.
4.2. Simulation
Dynamic behavior results from applying the rules described above and updating system's state each (simulated) time step. At each time step,  , the following sequence of events is followed:
, the following sequence of events is followed:
- Housing demand increases as a result of population growth.
- New land cells are developed according to the developers' preferences and available savings.
- Savings are updated.
- Attributes of developed land cells are updated.
- Developed land units are assigned to demand, and land prices are updated.
In the algorithm above, the attributes of land cells are updated using the idea of neighborhood, also used by cellular automata models, and which is defined as those cells whose attributes change instantly whenever a neighbor cell changes its state/activity [15]. This neighborhood approach gives the model a spatial dimension, in addition to the dynamic dimension added by increasing simulated time. Land development decisions change a cell's attributes, but they also influence the neighborhood attributes, as depicted in Fig. 3.
The model runs for 400 time steps with a time step of 1.
5. RESULTS
In this section, we run the simulation using three different scenarios for the model parameters. The results we present here illustrate how small changes in the parameters of the model described above result in different urban configurations. For the base case, developers of low-income neighborhoods look for land units with the lowest cost, and assign low weight to land attributes such as distance to the nearest working center (industry or commerce unit), density, and attractiveness. Developers of high-income neighborhoods, by contrast, assign a high value to land attributes.
There are no budget constraints in the base case. Developers build new units considering only the demand of housing, and labor demand from industries. Table 1 shows the values of the parameters for the base case.
Table 1. Values of the parameters for the basic model
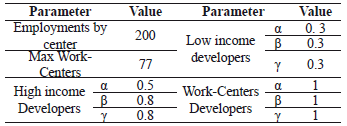
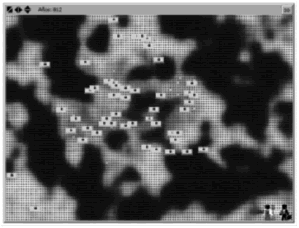
Low and high income neighborhoods grow from this initial configuration. Figure 2 shows the results by the end of the simulation. As can be seen in Fig. 4, high-income residences (light gray) are closer to the work centers, than low-income buildings (dark gray). The value of land is higher for work centers, followed by high-income neighborhoods and low-income neighborhoods. This behavior is consistent with results reported in the literature [12,13,15].

Figure 4. Base scenario, simulation results
Results in Fig. 4 correspond to a simulation length of 400 time steps. If we extend the simulation time to 800 periods, the city reaches its limits to growth, which are given by the fixed amount of land. These results are shown in Fig. 5.
The results above assume that all new housing units are assigned, regardless of people's income. Similarly, new houses are built independently of developers' income. A more realistic assumption would be to assign a value to the income attribute, and to allow both households and developers to save their disposable income in order to reinvest it in property or development. In a second scenario, households earn an average income, which depends on the number of work centers in the city. City growth is completely endogenous, and does not depend on exports.
In this second scenario, both developers and households are constrained by their income. If there is not enough demand, developers cannot build new housing units. Similarly, income restricts people's choices of the type of residences they can afford. Only people with high income can invest in high-income residences or build new work centers. The results of the simulation with these assumptions, and the same initial conditions of a basic scenario are shown in Fig. 6. As Fig. 6 shows, segregation is higher in this scenario. High-income neighborhoods occupy locations near industrial (including commerce) centers. These industrial centers tend to agglomerate forming a city centre, which is surrounded by low-income neighborhoods. Notice that the average distance of low-income neighborhoods to the city centre increases with respect to Fig. 4.

Figure 6. Scenario 2 (income constraints), simulation results
For the third scenario (Scenario 3, strategic infrastructure), we assume that developers of industrial or commercial units have a preference for strategic urban infrastructure. In this case, developers of commercial units prefer to be near the main road of the city, and still value low-priced land. In addition, the parameters for developers are modified. As is depicted in Table 2, for the third scenario, the developers of low-income neighborhoods look for land units nearest to working centers, and assign low weight to density and attractiveness. Developers of high-income neighborhoods, by contrast, assign a high value to density and attractiveness.
Table 2. Parameters of Scenario 3 (strategic infrastructure)
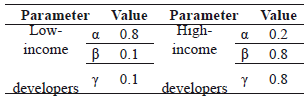
Figure 7 shows the final urban configuration with the assumptions of Table 2. Work centers are located near the main road, and low-income neighborhoods grow around them. High-income neighborhoods move to the suburbs.

Figure 7. Simulation results for the strategic infrastructure dcenario (Scenario 3)
The segregation of low and high-income neighborhoods observed in Fig. 7 is produced by the increase of the weight of attractiveness in the utility function of developers of high-income neighborhoods..
6. CONCLUSIONS
In this article we illustrate the capability of agent-based simulation for studying the behavior of complex social systems. The land-use model we present is a simplified model of the decisions made by urban developers. The behavior of agents is based on economic theory, such as utility maximization, and on dynamic rules that establish how state and auxiliary variables are updated. Agents' preferences over land attributes are represented by a Cobb-Douglas utility function and uncertainty in decision-making is modeled by examining random samples of available land. In addition to the dynamic rules for updating the state of the system along time, the model has a spatial dimension and changes in the attributes of a land cell also affect the state of neighboring cells. As results show, the agent-based model allows for a wide range of settings that lead to different spatial and social configurations of the city from the same initial conditions. The model is able to reproduce the segregation patterns predicted by other land-use models, which, along with other behavioral tests reported in Liévano (2010), supports the validity of the assumptions and the model structure. Future work includes testing the model with GIS data from a real location, and estimating the parameters of utility functions using real and experimental data.
ACKNOWLEDGEMENTS
This work has been funded by the Center for Research in Complexity (CeiBa).
REFERENCES
[1] Agarwal, C., Green, G., Grove, M., Evans, T y Schweik, C. A review and assessment of land-use change models dynamics of space, time, and human choice. Center for the Study of Institutions. Population, and Environmental Change, Indiana University, Bloomington, Indiana. pp. 22 -32, 2000. [ Links ]
[2] Von Thunen, J. Der Isolierte Staat in Beziehung auf Landwirtschaft und Nationalokonomie, Hamburgo, Puthes. pp: 1 - 56, 1826. [ Links ]
[3] Weber, A.Uber den Standort der industrien (Tubingen). English translation (1957) The theory of the location of industries (Chicago). pp. 32-63, 1909. [ Links ]
[4] Reilly, W. The law of retail gravitation (New York). pp. 96-123, 1931. [ Links ]
[5] Christaller, W. Die zentralen orte in sudden deutschland. English translation by BASKIN, C. W. Central places in southern Germany (New Jersey). pp 6-33, 1933. [ Links ]
[6] Losch, A. The economics of location (New Haven). pp. 32-102. 1954. [ Links ]
[7] Hoyt, H. The structure and growth of residential neighborhoods in American cities", Washington, U.S. Government Printing Office. pp. 23-45, 1939. [ Links ]
[8] Komei, Sasaki. A Comparative Static Analysis of Urban Structure in the Setting of Endogenous Income. JUE, 22, pp. 53-72, 1987. [ Links ]
[9] Alonso, W. Location and Land Use. Cambridge, MA: Harvard University Press. pp. 96-114, 1964. [ Links ]
[10] Lowry, I. A model of a metropolis, RM-4035-RC, Santa Mónica, Rand Cooperation: traducción italiana: Modello di una metropolis, Nápoles, Guida Editori (1972). pp. 43 - 72, 1964. [ Links ]
[11] Anas, A. Dynamics of Urban Residential Growth. JUE, January, pp. 66-87, 1978. [ Links ]
[12] Anas, A y Kim, I. General equilibrium models of polycentric urban land use with endogenous congestion and Job agglomeration. Journal of Urban Economics. V. 40, pp: 232-256, 1996. [ Links ]
[13] Clarke, M y Wilson, A. The dynamics of urban spatial structure: the progress of a research program. Transactions of the Institute of British Geographers, New Series, V. 10, No. 4, pp: 427-451, 1985. [ Links ]
[14] Forrester, J. Urban dynamics. Portland. pp. 87 - 154, 1969. [ Links ]
[15] Batty, M. Cities and Complexity. Massachusetts: MIT, 2005. [ Links ]
[16] Lin, L., Sato, Y y Zhub, H. Simulating spatial urban expansion based on a physical process. Landscape and Urban Planning, pp: 67-76, 2003. [ Links ]
[17] Durfee, E. H. A Unified Approach to Dynamic Coordination: Planning Actions and Interactions in a Distributed Problem Solving Network, Ph.D. dissertation, Department of Computer and Information Science, University of Massachusetts, 1987. [ Links ]
[18] Durfee, E. H., y Lesser, V. Negotiating Task Decomposition and Allocation Using Partial Global Planning. In Distributed Artificial Intelligence, Volume 2. pp. 229-244. San Francisco, Calif. 1989. [ Links ]
[19] Durfee, E. H., Lesser, V. R. y Corkill, D. D. Coherent Cooperation among Communicating Problem Solvers. IEEE Transactions on Computers C-36(11). pp. 1275-1291. 1987. [ Links ]
[20] Durfee, E. H. Coordination of Distributed Problem Solvers. Boston: Kluwer Academic. 1988. [ Links ]
[21] Gasser, L. Social Conceptions of Knowledge and Action. Artificial Intelligence 47(1-3), pp: 107-138, 1991. [ Links ]
[22] Decker, K., and Lesser, V. Designing a Family of Coordination Algorithms. In Proceedings of the First International Conference on Multiagent Systems, pp. 73-80, 1995. [ Links ]
[23] Bonasso, R. P., Kortenkamp, D., Miller, D. P., and Slack, M. Experiences with an Architecture for Intelligent, Reactive Agents. In Intelligent Agents II, eds. M. Wooldridge, J. P. Muller, and M. Tambe, pp. 187-202. Lecture Notes in Artificial Intelligence 1037. New York: Springer-Verlag, 1996. [ Links ]
[24] Jennings, N. Controlling Cooperative Problem Solving in Industrial Multiagent Systems Using Joint Intention. Artificial Intelligence 75(2). pp. 195-240, 1995. [ Links ]
[25] Bharwani, S., Bithell, M., Downing T., New M., Washington, R y Ziervoge G. Multi-Agent Modelling of Climate Outlooks and Food Security on a Community Garden Scheme in Limpopo, South Africa. Philosophical Transactions: Biological Sciences, Vol. 360, No. 1463, Food Crops in a Changing Climate, pp. 2183-2194, 2005. [ Links ]
[26] Liu, W y Williams M. A Framework for Multi-Agent Belief Revision Author(s): An International Journal for Symbolic Logic, Vol. 67, No. 2, On Commonsense Reasoning 1, pp. 291-312, 2001. [ Links ]
[27] Sycara, K. Negotiation Planning: An AI Approach. European Journal of Operational Research 46(2). pp. 216-234, 1990. [ Links ]
[28] Tesfatsion, L. (2008): Agent-based computational economics: a constructive approach to economic theory. Handbook of Computational Economics, Capt. 50. [ Links ]
[29] Batty, M. Agents, Cells and Cities: New Representational Models for Simulating Multi Scale Urban Dynamics. UCL working paperspaper. Centre for Advanced Spatial Analysis University College London. pp. 3 - 35, 2003. [ Links ]
[30] Liévano, F. Análisis de dinámicas urbanas y su impacto en el desarrollo sostenible por medio de simulación. Thesis (Maestría). Available under License. http://www.bdigital.unal.edu.co/3755/. 2011. [ Links ]
[31] Wilensky, U. NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modelling, Northwestern University, Evanston,IL, 1999. [ Links ]
[32] Macal, C. M. y North, M. J. (2006): Tutorial on agentbased modelling and simulation part 2: How to model with agents, in L. F. Perrone, F. P. Wieland, J. [ Links ]
[33] Duffy, J. Agent-Based models and human subject experiments. Handbook of Computational Economics, V. 63. pp. 88-108. Pittsburgh, 2008. [ Links ]
[34] Brenner, T. Agent learning representation: advice modelling economic learning. Handbook of Computational Economics, Capt. 53. Jena, 2008. [ Links ]
[35] Genesereth, M. R y Ketchpel, S. P. (1994): Software Agents. Communications of the ACM 37(7), pp: 48-53, 1994. [ Links ]
[36] Briassoulis, H. Analysis of land use change: theoretical and modelling approaches. Web Book of Regional Science. pp. 1 - 23, 2009. [ Links ]
[37] Herden, G., Knoche, N., Seidl, C y Trockel, W. (1999): Mathematical utility theory: utility functions, models and applications in the social sciences. Journal of Economics Zeitschrift für Nationalökonomie Sulementum, Sulement 8. Springer. [ Links ]
[38] Felsen, M y Wilensky, U. NetLogo urban suite - economic disparity model. http://ccl.northwestern.edu/netlogo/models/UrbanSuite-EconomicDisparity. Center for Connected Learning and Computer-Based Modelling, Northwestern University, Evanston, IL, 2007. [ Links ]