Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.79 no.174 Medellín jul./ago. 2012
SIMULATION OF HYDRODYNAMIC CONDICTIONS AT SANTA MARTA COASTAL AREA (COLOMBIA)
SIMULACIÓN DE LAS CONDICIONES HIDRODINÁMICAS EN EL AREA COSTERA DE SANTA MARTA (COLOMBIA)
FRANCISCO GARCÍA
MSc. Professor, Universidad del Magdalena, , fcofdogarcia@yahoo.com
CARLOS PALACIO
Ph.D. Professor, Universidad de Antioquia, cpalacio@udea.edu.co.
URIEL GARCIA
Biologist, Professor, Universidad del Magdalena, uriel.garcia@yahoo.es
Received for review August 8th, 2011, accepted May 30th, 2012, final version July, 5th, 2012
ABSTRACT: Hydrodynamic conditions of Santa Marta coastal area were determined using a 3D hydrodynamic model, RMA10. The model was previously calibrated and validated for two different periods (dry season and rainy season). A good fit between measurements and simulations was found. For the year 2001, the model predicted current magnitude and current velocity at 40 meters deep in the water column. A maximum current magnitude of 12 cm/s was found. Current magnitude distribution showed an occurrence of 30%, for ranges of 2 and 4cm/s, and 4 and 6cm/s. Speeds up to 12 cm/s appeared with a frequency lower than 1%. In the analysis of simulated data it was found that the major axis direction of the current was from 62 to 242 degrees.
KEYWORDS: RMA10, Calibration, Validation, Currents.
RESUMEN: Se determinaron las condiciones hidrodinámicas del Área Costera de Santa Marta, mediante el uso de un modelo hidrodinámico 3D. El modelo RMA10 fue previamente calibrado y validado para dos periodos diferentes del año (Época seca y de lluvias). Se encontró un buen grado de acercamiento entre las mediciones y las simulaciones. Para el año 2001 el modelo predijo las condiciones de magnitud y velocidad de corriente a 40 metros de profundidad en la columna de agua, encontrando corrientes máximas de 12 cm/s. La distribución de las magnitudes de corrientes mostraron una ocurrencia del 30% para el rango entre 2 y 4 cm/s, al igual que entre 4 y 6 cm/s, el eje principal de corriente fue 62-242 grados.
PALABRAS CLAVE: RMA10, Calibración, Validación, Corrientes.
1. INTRODUCTION
At a macro scale, Caribbean Sea circulation and patterns, including the Colombian basin, have been reasonably well studied and documented by different authors, among them Gordon [1], Murphy et al. [2], Andrade and Barton [3], and Johns et al. [4]. But there is little knowledge of the micro scale, in reference to direction and magnitude of the current at Santa Marta’s coastal area (ACSM), which includes Santa Marta and Taganga bays (BSMyT). In BSMyT, hydrodynamic conditions are virtually unknown, since there is little available and reported information for this specific zone [5].
The environmental importance of knowing ocean currents lies on the fact that they influence processes such as transportation and dispersion of hydrocarbons spills and the dilution in faraway places of domestic residual waters spilled in the ocean through submarine agents [6]. In fact, measurements of ocean currents have been used in engineering to design marine outfall [6, 7] and to generate energy through the waves [8]. The need to know the circulation patterns is also evident in other different branches of science, such as marine geology, in order to determine the transport and sediment deposition processes. However, currents have not been either characterized or extensively measured in the ocean, mainly due to technological and economic limitations [6].
One alternative to predict hydrodynamic conditions in coastal zones is the use of numerical models. Models should be calibrated and validated before they are applied to the study of a specific situation. However, there is not a defined process to carry out this work [12]. Calibration varies depending, on one hand, on water body characteristics and on data availability, and on the other hand, on the perception, opinion, and experience of the modeler [12]. This paper illustrates implementation, calibration, validation, and application of a 3D hydrodynamic model, RMA10, to simulate ACSM hydrodynamic conditions.
2. MATERIALS AND METHODS
2.1 Study area
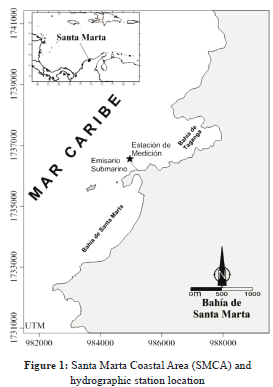
ACSM is located between 11.21 and 11.31 north latitude and 74.18 and 74.24 west longitude, in the Caribbean Sea. Its location can be seen in figure 1. In this figure, the location of the measuring station (11.23 Lat., 74.22 Lon.) used to calibrate and validate the hydrodynamic model is also shown. The ACSM conformation is open, but it has a coastal line, limited to the north and to the south by rocky formations. Sandy beaches and denudational forms exposed to marine waves and winds are more predominant in the ACSM central part. There are often cliffs formed by phyllites in the Sierra Nevada foothills and also hills or small islands molded by the sea. The topography of the coast is heterogeneous due to “Sierra Nevada de Santa Marta” foothills, which generate formations of cliffs, bays, small islands, and inlets, which at west sides are more exposed to the action of winds and marine waves [13]. The climate regime is characterized by a dry season (December-April), in which the “Alices” (north east winds) produce the local phenomenon of upwelling, reduce the water temperature (20°-25°C), and increase wave intensity and salinity (up to 38 UPS). In the rainy season (May-November) upwelling stops; the water is warm (27°-29°C) and the salinity drops to 34 UPS [13].
2.2. Numerical model
The model “RMA10” was used, this model predicts state variables, pressure, and velocity in three dimensions, by solving a group of equations based on: Navier-Stokes’ equations, mass conservation equation, advection-diffusion equation, and state equation (in order to relate density, salinity, temperature, and suspended sediments). Bottom roughness, Coriolis effect, and roughness induced by the wind on the free surface, are also included in the model [14]. This model estimates levels of free surface and horizontal components of speed of the to sub-critical flow in tridimensional fields of flow. Hydrodynamic equations are solved by finite element method through Galerkin’s method of weighed residuals. Spatial integration is carried out by Gauss’s integration. The solution is totally implicit and the group of simultaneous equations is solved by the Newton-Raphson nonlinear iteration. Spatial integration is performed using Gauss quadrature method, by customizing the unsteady variables in time using the Crank-Nicholson modified method [14, 15]. The governing equations, in differential form, are shown in equations (1) to (6).
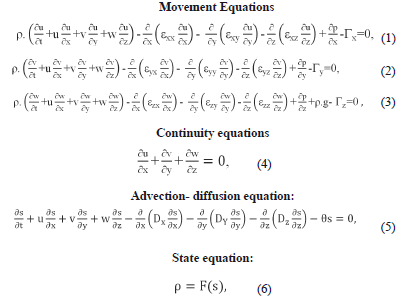
Where x, y, z = Cartesian system coordinates; u, v, w = velocities in the directions of the Cartesian coordinate system; t= time; P= water pressure; DX, DY, DZ, = Eddy diffusion coefficients; εxx, εxy, εxz, εyx, εyy, εyz, εzx, εzy, εzz = Eddy turbulence coefficients, g= acceleration due to gravity; r = water density; Gx, Gy, Gz = external forces; S= salinity, and s = source/salinity drain.
The RMA10 model has been widely used in the solution of problems in order to simulate hydrodynamic conditions in coastal environments [14, 16-18]. Its detailed description and the reference of its numerical solution may be consulted in Fossati, et. al. [14].
2.3 Bathymetry and numerical grid
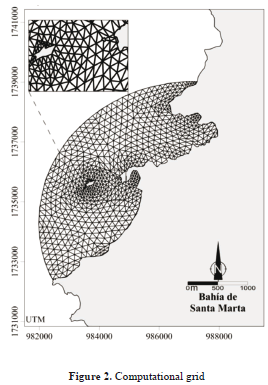
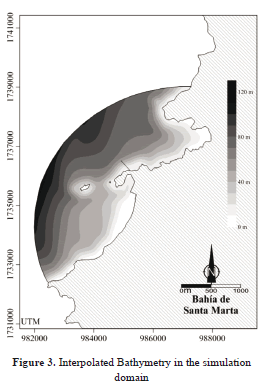
The bathymetry was taken from COL406 and COL244 nautical charts of the CIOH, which were digitalized in plane coordinates. In order to determine the spatial resolution of the computational grid, the procedure suggested by García et al, [19] was followed. A grid was used with 1,576 elements, 3,378 interpolation points, and 8 layers with thicknesses from 0.05 to 15 meters in the deepest zones, and element sizes between 10 and 160 meters (see figure 2). The interpolated bathymetry in simulation domain is shown in figure 3.
2.4 Field Measurements
Field data was provided by four measurement campaigns. Two of them were used to calibrate the model (from January 7th to February 7th, and from October 13th to November 14th, 2009); the other two were used for validation (from February 11th to March 12th, and from November 16th to December 16th, 2009).
Data collection periods for calibration and validation were in the dry season, December–April, (in which there is an important thermohaline circulation caused by the upwelling phenomenon) and in the rainy season, May – November, (characterized by a vertical stratification of the water column). In order to determine direction and magnitude of currents in the field an RCM9 LW continuous measurement current meter (Aanderaa), located 10 meters from the bottom (40 meters deep) and suspended by buoys, was used for such a purpose. An anchorage system was estimated and designed, according to techniques described by Neshyba and Fonseca [20]. RCM9 was fitted with sensors of temperature, salinity, pressure, and dissolved oxygen. Measurements were made in 10 minutes intervals.
2.5 Calibration
Calibration of the RMA10 model was made using measurements of tide and currents for 30 continuous days, in dry season (from January 7 to February 7, 2009), and in rainy season (from October 13 to November 14, 2009). In this process, simulation results were compared with field measurements. The parameters used in the adjustment during the calibration were bottom roughness and turbulent diffusion coefficients. These parameters were varied, through error assay, until an acceptable fit between simulations and measurements was found. In order to quantify the exactness of the model, error calculators such as “Root Mean Square” (RMS) [21, 22] and the predictive ability “Skill” [22] were used. The RMS expression is shown in equation (7), while the Skill quantification was made according to equation (8).
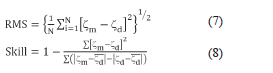
Where and are the water levels (in meters), measured with the equipment and obtained in simulations, respectively, N is the number of samples in the time series, and corresponds to the temporal mean of simulated water levels. If the “RMS” resulted less than a 5%, the correlation between data measured and simulated was considered excellent. If the “RMS” value was between 5 and 10%, the correlation between the data measured and simulated was considered very good. A perfect correlation between measured data and predictions generates a “Skill” value of one; on the contrary, a complete mismatch between time series results in a “Skill” value of zero. “Skill” values higher than 0.95 may be considered as an excellent fit of predictions with data measured in the field [22].
The wind field acting on the water surface were generated from the NCEP/NCAR reanalysis, corrected according to Simionato et al., [23] (this was done because the wind intensity data is underestimated by NCEP/NCAR reanalysis). A discussion on the quality of these data may be found in Kalnay [24] and Simmonds and Keay [25]. The temporal interval in NCEP/NCAR files is 360 minutes (6 hours). Data base corresponds to a T62 Gaussian grid with 192 x 94 points located within 88.54N and 88.54S latitude and 0.0Eand 358.125E longitude. The wind velocity was transformed to wind stress using the equations (9) and (10):
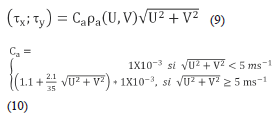
Where, are wind stress coefficients in X and Y directions respectively, Ca is the wind drag coefficient, ra is the density of the air; U, V are the components of wind velocity in the X and Y directions respectively.
The information about the tide, for open boundary conditions, was provided for the regional model of the Caribbean Sea by a one way coupling scheme [5]. Salinity and temperature data, extracted from the Real Time Ocean Forecast System (RTOFS) for the North Atlantic (which is based on predictions of the Hybrid Coordinate Oceanic Model (HYCOM) [26]) were also used under open boundary conditions.
2.6 Validation
The ACSM 3D model was validated through simulations of currents and and water level of the sea surface, without changing the conditions of the physical and numerical parameters determined in calibration. 30 day simulations were carried out in periods of spring and neap tides for two different seasons of the year: the dry season (from February 11 to March 12, 2009) and the rainy season (from November 16 to December 16, 2009). The model fit during the validation process was calculated with “RMS” and “SKILL” [21, 22].
3. RESULTS
3.1. Calibration
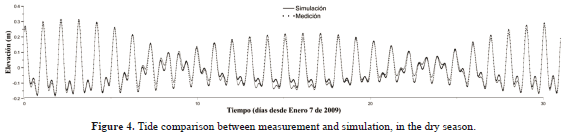
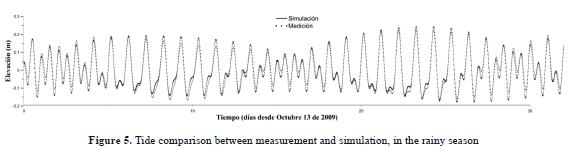
Figures 4 and 5 show a good fit between the tide produced by the model and field measurements, for the dry and rainy seasons, respectively. “RMS” error was calculated as 1.95 cm (dry season) and 2.15 cm (rainy season). In both cases, discrepancies were lower than 5% of the tide amplitude which indicates a good calibration process. This was confirmed through the predictive ability, “Skill”, with values of 0.992 for dry season and 0.987 for rainy season.
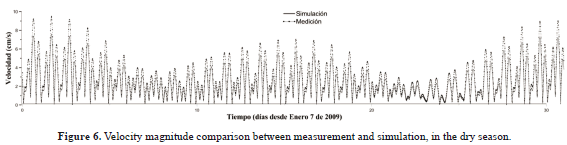
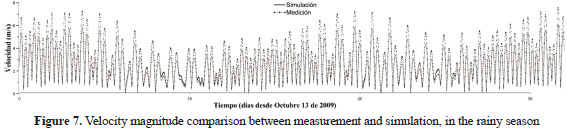
Data comparisons of measured and simulated speeds (similarly to the analysis of tides) were done. A good correlation was found, with RMS of 0.69 for comparisons in the dry seasons (figure 6) and 0.70cm/s for comparisons in the rainy seasons (figure 7), with a predictive ability, “Skill”, of 0.947 for both.
3.2. Validation
The validation process confirms a good fit between field measurements and simulation results. Both, “RMS” error and predictive ability “Skill”, showed the good capacity of the model to represent the hydrodynamic conditions, measured in the field.
3.3. Simulation of Currents Pattern
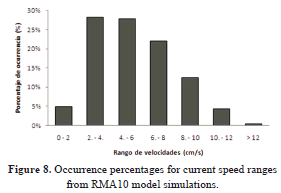
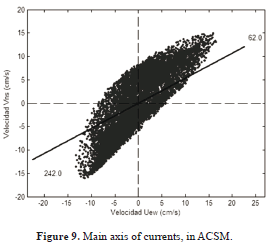
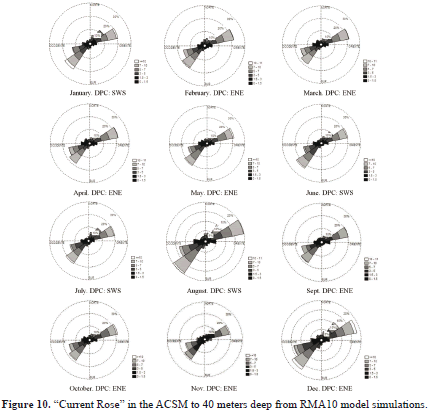
The model was used to simulate currents at the depth of 40 meters in ACSM. The model was run twelve times in order to generate direction time series and current magnitudes, for each month of the year 2011. The current magnitude distribution showed an occurrence of 30%, for ranges of 2 and 4cm/s, and 4 and 6cm/s. Speeds up to 12 cm/s appeared with a frequency lower than 1% (see figure 8). In the analysis of the simulated data it was found that the major axis direction of the current was from 62 to 242 degrees (figure 9). The Direction of the Predominant Current (DPC) was SWS for January and from June to August. The remaining monthly periods have a DPC in ENE direction (figure 10).
4. DISCUSSION
The RM10 model was calibrated and validated using the hydrodynamic conditions of Santa Marta bay. Error calculations between the simulated and measured data show a good fit between them. Both, calibration and validation were made using currents field measurement 40 meters deep in the water column. This fact may become a limitation for using the model since ACSM presents some periods of vertical stratification which coincide with rainy seasons, and during these periods there are two water masses with different densities that differentiate the conditions of water column. However, this is the first research carried out in ACSM investigating its hydrodynamic conditions.
ACKNOWLEDGEMENT
The authors thank COLCIENCIAS, Universidad del Magdalena, and Universidad de Antioquia, for financing this research.
REFERENCES
[1] Gordon, L.A., Circulation of the Caribbean Sea, Journal of Geophysical Research, 72, pp. 6207-6223, 1967. [ Links ]
[2] Murphy, F., Hurlburt, H.E. and Obrien, J.J., The connectivity of eddy variability in the Caribbean Sea, the Gulf of Mexico, and the Atlantic Ocean, Journal of Geophysical Research, 104, pp. 1431-1453, 1999. [ Links ]
[3] Andrade, C.A. and Barton, E.D., Eddy development and motion in the Caribbean Sea, Journal of Geophysical Research, 105, pp. 26191-26201, 1999. [ Links ]
[4] Johns, W., Lee, T.N., Schott, F.A., Zantopp, R.J. and Evans, E., The North Brazil Current retroflection: Seasonal structure and eddy variability. Journal of Geophysical Research. 95, pp. 22103-22119, 1990. [ Links ]
[5] Garcia, F.F., Palacio, C. y Garcia, U., Uso de un modelo regional para el mar Caribe para obtener condiciones fronteras abiertas en un modelo local para la bahía de Santa Marta – Colombia, Boletín Científico CIOH, 26, pp. 33-46, 2008. [ Links ]
[6] Chin, D.A. and Roberts, D.W., Time series modeling of coastal currents, J. Waterway, Port, Coastal and Ocean Eng., 111(6), pp. 954–972, 1985. [ Links ]
[7] Prandle, D. and Eldridge, R., Use of surface currents measured by HF Radar in planning coastal discharges, Marine Pollution Bulletin, 18(5), pp. 223–229,1987. [ Links ]
[8] Polo, J.M., Rodriguez, J. y Sarmiento, A., Potencial de generación de energía a lo largo de la costa colombiana mediante el uso de corrientes inducidas por mareas, Rev. Ing., 28, pp. 99-105, 2008. [ Links ]
[9] Fajardo, G., Surgencia costera en las proximidades de la península colombiana de La Guajira, Bol. Cient. CIOH, 2, pp. 7-19, 1979. [ Links ]
[10] Arévalo, D. y Franco, A., Características oceanográficas de la surgencia frente a la ensenada de Gaira, departamento del Magdalena, época seca menor de 2006, Boletín de Investigaciones Marinas y Costeras, 37(2), 2008. [ Links ]
[11] Cabrera, E. and Donoso, M., Estudio de las características oceanográficas del Caribe colombiano, Región III, Zona 1, PDCTM, Bol. Cient. CIOH, 13, pp. 19-32, 1993. [ Links ]
[12] Hsu, M.H., Kuo, A.Y., Kuo, J.T. and Liu, W.C., Procedure to calibrate and verify numerical models of estuarine hydrodynamics. Journal of Hydraulic Engineering, pp. 166–182, 1999. [ Links ]
[13] Vega, J., Rodriguez, A., Reyes, M.C. y Navas, R., Formaciones coralinas del área de Santa Marta: estado y patrones de distribución espacial de la comunidad bentónica, Bol. Invest. Mar. Cost., 37, pp. 87-105, 2008. [ Links ]
[14] Fossati, M. and Piedra, I., Numerical modelling of residual flow and salinity in the Rio de la Plata, Applied Mathematical Modelling. 32, pp. 1066–1086, 2008. [ Links ]
[15] Palacio, C., Garcia, F.F. y García, U., Calibración de un modelo hidrodinámico 2D para la bahía de Cartagena, DYNA, 164, pp. 152166, 2010. [ Links ]
[16] Miller, B., Pierson, W., Wang, Y. and Cox. J., An Overview of Numerical Modelling of the Sydney Deepwater Outfall Plumes, Marine Pollution Bulletin, 33, pp. 147-159, 1996. [ Links ]
[17] Cook, C.B., Orlob, G. and Huston, G., Simulation of wind-driven circulation in the Salton Sea: implications for indigenous ecosystems, Hydrobiologia, 473, pp. 59–75, 2002. [ Links ]
[18] Teeter, A.M., Johnson, B., Berger, C., Stellin, G., Scheffner, W., Garcia, M. and Parcchure, T., Hydrodynamic and sediment transport modeling with emphasis on shallow-water, vegetated areas (lakes, reservoirs, estuaries and lagoons), Hydrobiologia, 444, pp. 1–23. [ Links ]
[19] Garcia, F.F., Palacio, C. y Garcia, U., Generación de mallas no estructuradas para la implementación de modelos numéricos. Dyna, 157, pp. 17-25, 2009. [ Links ]
[20] Neshyba, S. y Fonseca, T., Corrientes costeras: Manual de mediciones y Análisis, Inv. Mar. Valparaíso, 7, pp. 1979-1986, 1981. [ Links ]
[21] Li, M., Zhong, L. and Boicourt, W., Simulations of Chesapeake Bay estuary: sensitivity to turbulence mixing parameterizations and comparison with observations, Journal of Geophysical Research, 110, pp. 27-36, 2005. [ Links ]
[22] Dias, J.M., Sousa, C.M., Bertin, X., Fortunato, X. and Oliveira, V., Numerical modeling of the impact of the Ancão Inlet relocation (Ria Formosa, Portugal), Environmental Modelling and Software, 24, pp. 711–725, 2009. [ Links ]
[23] Simionato, C., Meccia, V., Dragani, W. and Nuñez, M., On the use of the NCEP/NCAR surface winds for modeling barotropic circulation in the Río de la Plata, Estuarine Coastal Shelf Sci., 70, pp. 195-206, 2006. [ Links ]
[24] Kalnay, E., Kanamitsu, M., Kistler, R., Collins, M., Deaven, D. and Gandin, L., The NCEP/NCAR 40-year reanalysis Project, Bull Am Meteorol Soc, 77, 437-71, 1996. [ Links ]
[25] Simmonds, I. and Keay, K., Mean Southern Hemisphere extratropical cyclone behavior in the 40-year NCEP-NCAR Reanalysis, J. Clim., 13, pp. 873-885, 2000. [ Links ]
[26] Mehra, A. and Rivin, I., A real Time Ocean Forecast System for the North Atlantic Ocean, Atmos. Ocean. Sci., 21, pp. 211-228, 2010. [ Links ]