DEFINICION Y ANALISIS DE UNA FUNCION DE EVOLUCION DE SOLUTOS DISPERSIVOS EN FLUJOS NATURALES

DEFINITION AND ANALYSIS OF AN EVOLUTION FUNCTION OF DISPERSIVE SOLUTES IN NATURAL FLOWS

 

ALFREDO JOSÉ CONSTAIN ARAGÓN
Ingeniero, Director I+D, Hydrocloro Technologies, Bogotá, Colombia, alfredo.constain@gmail.com

 

Recibido para revisar Enero 26 de 2012, aceptado Septiembre 11 de 2012, versión final Septiembre 13 de 2012

 

---

RESUMEN: Dados los agudos y crecientes problemas de deterioro del agua en el mundo industrializado moderno se hace indispensable acopiar un conocimiento profundo de los mecanismos de dispersión de los solutos en los flujos naturales que permita predecir y controlar las variables asociadas a las contaminaciones hídricas. En este artículo se plantea la definición de una función especial que guía la evolución energética de este fenómeno y por lo tanto tiene gran aplicación en los actuales estudios de calidad del agua. Esta función tiene la ventaja de ser una expresión matemática sencilla, con gran generalidad y de poder ser interpretada de una forma muy intuitiva. Se presenta la aplicación práctica de estos conceptos a un pequeño rio de montaña, cumpliéndose satisfactoriamente la validación experimental requerida, para etapas iniciales de formación de la pluma.

PALABRAS CLAVE: Dispersion, dinámica Gaussiana, estudios de calidad de aguas.

ABSTRACT: Given the acute and increasing problems of decline of water in the industrialized modern world it is indispensable to gather together a deep knowledge of those dispersion mechanisms of solutes in natural flows that allows predict and control those variables associated with hydric contaminations. In this article it is stated the definition of a special function that drives the energetic evolution of this phenomenon and then it has a wide application in present water quality. This function has the advantage to be an easy mathematical expression, with great generality and also to be interpretate with a very intuitive reasoning. It is presented a practical application of these concepts to a small mountain stream accomplishing satisfactory the required experimental validation, to earlier stages of tracer plume formation.

KEYWORDS: Dispersion, Gaussian dynamics, water quality studies.

---

 

1. INTRODUCCIÓN

Cuando ocurre un vertimiento súbito de un soluto conservativo a un flujo turbulento, a partir de la ruptura del equilibrio químico ocurren diversos fenómenos que deben ser identificados y descritos para entender su desarrollo cuantitativo en el eje longitudinal.

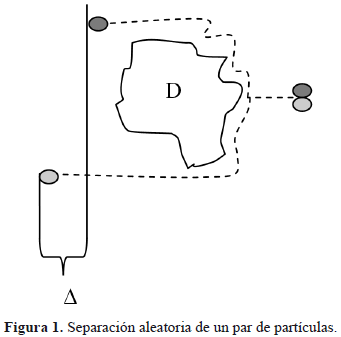
Una vez que el soluto penetra al agua a partir de una solución inicial (en la que ya ha ocurrido la solvatación inicial de la sustancia considerada) comienzan a actuar los mecanismos de dispersión de las partículas basados en la separación aleatoria de cualquier par de ellas por efecto de la distribución de velocidades del flujo actuando en un líquido cortante, mediante la acción de la viscosidad sobre un elemento cualquiera de difracción, D, Figura 1. [1].

En tal contexto es posible demostrar que definiendo la separación característica D de estas dos partículas en un tiempo t correspondiente vale la siguiente expresión.

Y por lo tanto su distribución estadística tiene una naturaleza Gaussiana. Se puede definir entonces una velocidad de separación promedio de las partículas como:

Esta velocidad la llamaremos "Velocidad de dispersión del soluto" y como se relaciona con la curva Gaussiana que resulta, D y t se medirán en los puntos de inflexión de dicha curva, que es por lo tanto un punto característico de la métrica observada. Ahora, si se entiende que esta velocidad de dispersión tiene su origen en el efecto de la distribución de velocidades puntuales en cada punto del flujo, entonces es posible definir una función j que relacione V_disp y U, velocidad media advectiva del flujo que es el factor que a su vez define el campo de velocidades. Esta función se define entonces como la razón de las dos velocidades de la siguiente forma:

Sobre esta función se desarrollara el estudio de la evolución de la pluma de soluto en el flujo.

 

2. NATURALEZA DE j.

Si se mira el vertimiento súbito de la solución del trazador como un suceso del rompimiento del equilibrio químico en ese punto se puede entender a la velocidad V_disp como un mecanismo de restauración del equilibrio en el sistema. Este tipo de efectos es común en la fisicoquímica y son llamados "mecanismos de Le Chatelier" [2] que tienden a aminorar el factor que generó el desequilibrio inicial. El mecanismo en cuestión en este caso es la inserción súbita de una sustancia concentrada en un pequeño espacio del sistema, por lo tanto se puede identificar como la concentración de soluto la magnitud asociada al mecanismo detonante y en virtud de la característica reaccionante de V_disp esta tiene que oponerse a un aumento de concentración. Esto implica simplemente que la velocidad de dispersión ya definida debe propiciar la disminución de la concentración.

Al instante t=0 la V_disp=0 obviamente, pero en el instante siguiente esta velocidad tiene que aumentar para propiciar el alejamiento inicial de las partículas de soluto entre sí. Una vez consolidada esta situación, como al haberse separado las partículas se disminuye la concentración en el volumen considerado del sistema, momentos después V_disp no requiere tener tanta intensidad como al principio y comienza a descender su valor.

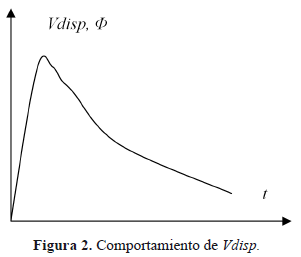
Así, en la medida en que se tenga cada vez menos concentración en el volumen, el sistema va requiriendo cada vez menos la acción restauradora de esta velocidad, hasta que finalmente se extingue en el equilibrio. Ver Figura 2.

Si se asume un valor de la velocidad advectiva media U, como constante entonces la función j tendrá la misma tendencia. Este tipo de curvas que comienzan en el mismo sitio en que terminan tienen una naturaleza termodinámica especial pues reflejan la variación del estado del sistema. Por lo tanto V_disp y j son funciones de estado que no dependen del tipo particular de proceso por el cual lleguen a un valor dado.

 

3. RELACION DE j CON LA DISPERSION.

La ecuación (1) puede escribirse en función del Coeficiente Longitudinal de dispersión, E como en (4):

Si esto es correcto entonces se puede establecer una ecuación para la velocidad media advectiva en (5):

Despejando a E:

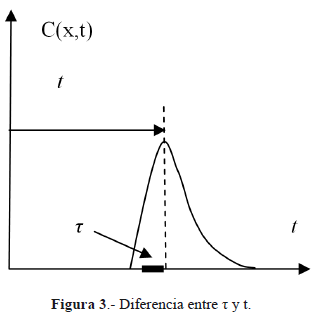
Debe notarse aquí que el tiempo característico Gaussiano t es diferente a la variable independiente t, ya que la primera se refiere al tiempo en el cual la separación aleatoria de las partículas ocurre mientras esta distancia promedio es D. Es como ya se dijo una escala temporal "propia" de la dispersión (línea gruesa sobre el eje del tiempo) en la cual ocurre el desperdigamiento del soluto por efecto del mecanismo de Le Chatelier, V_disp ya señalado, mientras que la escala temporal general (flecha larga) se asocia más bien al efecto advectivo de U. Figura 3.

El siguiente paso es calcular t en función de t. Una forma directa de estimar cuantitativamente estos tiempos es atraves de los tiempos de espera de un observador situado aguas abajo del punto de vertimiento para un determinado suceso que puede ser por ejemplo: "esperar por cero partículas", "esperar por una partícula", "esperar por 2 partículas", …"esperar por n partículas". En realidad el tiempo general t debe ser la suma de todos los tiempos de espera, calculados a partir del tiempo característico t. Como se tiene un esquema Gaussiano, entonces es factible utilizar una distribución de Poisson para este cálculo:

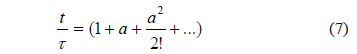
Donde a≈1.54 que es denominado "Número de Svedberg" [3] ya que fue este científico sueco quien lo hallo en sus famosas investigaciones sobre la distribución Browniana. Por lo tanto:

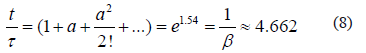
Esta expresión es importante para poderse relacionar con otras expresiones importantes de la teoría clásica del transporte de masa en los flujos naturales, como por ejemplo la función de Fick donde M es la masa de soluto y A es la sección transversal del flujo [4].

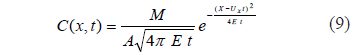
Entonces reemplazando la ecuación (6) en la (9) se tiene con:

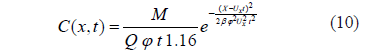
Esta es una ecuación de Fick modificada que tiene en cuenta la dependencia de la velocidad de dispersión con la velocidad media advectiva, tal como se ha explicado anteriormente.

 

4. DETERMINACION DE D Y T COMO FUNCIONES DE F.

Es importante establecer las relaciones entre los parámetros característicos de la dispersión, D y t en función de j y de las mediciones especificas que se hagan en las curvas Gaussiana, para tener una visión completa de la evolución de la pluma de soluto en el flujo.

Mirando el denominador en el argumento exponencial de la ecuación clásica de Fick (9) se puede establecer que:

Debe recordarse que aunque la ecuación de Fick es función del tiempo como variable independiente la dimensión cuadrática del numerador (y del denominador) en el argumento exponencial es espacio, por eso la desviación típica es en el eje X.

Teniendo en cuenta la ecuación (4) se puede escribir:

Ahora, a partir de las ecuaciones (2) y (3) se puede escribir:

Como en realidad la curva Gaussiana esta dibujada sobre el eje t y en el punto de inflexión se va a medir directamente es la desviación típica temporal s_t, es necesario poner a (12) y (13) en función de esta variable, si la relación entre ambas desviaciones es la velocidad advectiva:

Y

Las ecuaciones (14) y (15) son importantes porque permiten calcular parámetros dinámicos de la dispersión con base en mediciones temporales sobre la curva Gaussiana específica. Un hecho notable es que mientras D siempre es proporcional a la desviación típica s_t (si la velocidad es constante) t crece más rápido que dicha desviación pues j está siempre medida en su flanco descendiente. Esta circunstancia es la que permite que la velocidad dispersiva V_disp vaya disminuyendo en tanto el proceso se acerque al equilibrio. No obstante lo anterior, la relación entre t y t siempre se mantiene para cualquier situación. En puntos muy cercanos al vertimiento el tiempo t será muy pequeño implicando un movimiento muy rápido de las partículas de soluto alejándose cada par (tomado aleatoriamente) vertiginosamente para tratar de frenar el mecanismo causante del desequilibrio. En puntos más alejados este tiempo será mayor, implicando una mayor lentitud en esta acción.

 

5. ESTIMACION NUMERICA DE j DESDE VARIOS PUNTOS DE VISTA.

Cuando se propone una relación teórica como j es importante fijar valores numéricos tanto para el valor pico como para la tendencia decadente después del pico, sobre el supuesto que el flanco ascendente al inicio es muy rápido y no tiene ningún interés teórico especial.

Al principio del vertimiento súbito de soluto al flujo la desviación típica temporal s_t, medida sobre la curva Gaussiana será mucho mayor que t. Vale la pena preguntar cuál puede ser el mayor valor de esta función sabiendo además que t y t siempre tienen una relación constante (atraves de la constante b≈0.215).

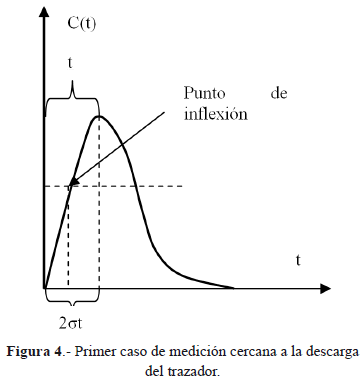
Supóngase primero que la masa de soluto se distribuye en un 95% aproximadamente sobre una extensión temporal de 2s_t (de acuerdo con la teoría Gaussiana corriente). En este caso se tiene la curva de la Figura 4.

Para este caso en el que en t=2s_t (medido también desde el origen hasta el pico de la curva) ya aparecen sobre el medidor las primeras partículas del soluto vale entonces:

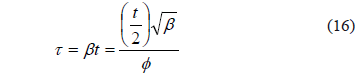
Despejando j:

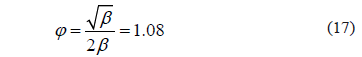
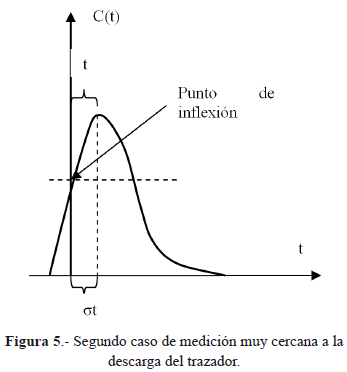
En un segundo experimento ideal hagamos penetrar la curva aun más cerca del origen y dejemos que t=s_t, según la Figura 5.

En este caso se tendrá idealmente:

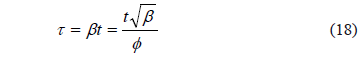
Despejando j:

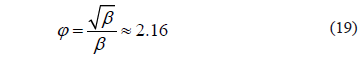
Naturalmente que se puede hacer penetrar más la curva hacia el origen pero de acuerdo con la ecuación (8) el valor temporal t es la unidad básica de medida para este proceso, por lo tanto no tiene sentido esta acción posterior. De acuerdo con esta afirmación (que deberá ser verificada experimentalmente) el valor máximo para j es 2.16 aproximadamente. Este máximo sugiere que en las primeras etapas de formación de la nube de soluto en un flujo turbulento la velocidad de separación de las partículas por efecto cortante en un campo de velocidad es alta y sobrepasa la propia velocidad advectiva promedio.

Es necesario ahora establecer las condiciones analíticas aproximadas que determinan la tendencia de la función en su flanco descendente.

A partir de la ecuación modificada de Fick se expresa el valor para la concentración pico, según la ecuación (10). Reubicando seguidamente a j:

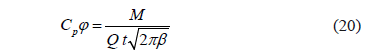
Multiplicando el numerador y denominador por a un factor de utilidad para aplicar las dos definiciones por aparte:

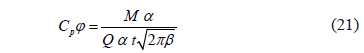
Se puede demostrar que:

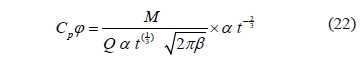
Definiendo por aparte:

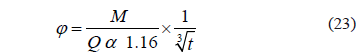
Y:

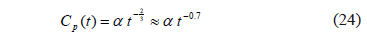
El coeficiente a se obtiene examinando cada caso experimental así:

Un valor más preciso es el valor promedio para este parámetro tomado en todas las n curvas de un experimento. Mientras que la ecuación (25) introduce el cálculo de a con base en los valores de concentración pico, la ecuación (23) define la tendencia teórica de j.

 

6. VERIFICACION EXPERIMENTAL DE LA CURVA DE j PARA UN PEQUEÑO CAUCE DE MONTAÑA.

Se escoge para esta verificación una serie de experimentos con trazador iónico (sal común) mezclado en un balde con un litro de agua aproximadamente, realizados en la quebrada "La Vieja" al nororiente de la ciudad de Bogotá en desarrollo de una tesis en Ingeniería ambiental [5] cuyo objetivo era verificar la validez experimental de la ecuación (10) en distancias cortas y largas a partir del punto de descarga del trazador.

El cauce escogido para las pruebas es un pequeño rio de montaña de ancho medio de W≈1.5 m, con una pendiente de régimen uniforme estimada en S≈2.6% (rugoso, baja velocidad), una velocidad media advectiva de U≈0.119 m/s y un caudal aproximado de Q≈43.0 l/s. Figura 6.

El caudal se midió asumiendo un trazador conservativo por la ley de conservación de la masa; la velocidad media se midió por el desplazamiento del pico de las curvas de trazador.

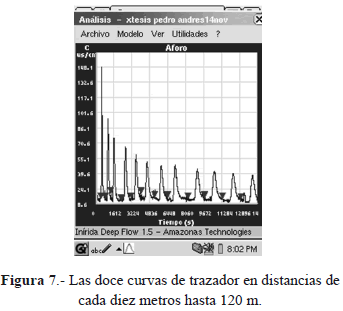
En esta jornada se hicieron vertimientos súbitos de masa de 200 gramos de sal común a través de un tramo de 120 metros, midiendo con un instrumento especial con conductivimetro las curvas de trazador cada diez metros desde el punto de inyección aumentando de a diez metros para completar 12 mediciones en 120 metros. El instrumento especial llamado "Inirida Deep Flow" muestra en pantalla todas las curvas sucesivas realizadas. Las flechas rojas son los instantes de inyección súbita del trazador. Figura 7.

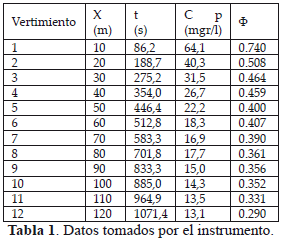
En el siguiente Tabla 1 se muestran los datos pertinentes encontrados en las experimentaciones correspondientes.

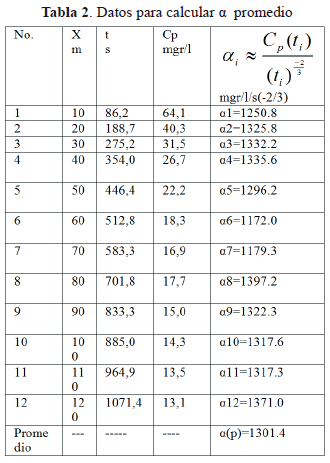
Ahora para calcular la formula teórica para j se requiere calcular el valor promedio de a a partir de los datos desarrollados en la Tabla 2.

La ecuación (23) de tendencia para el flanco decadente de j con los datos pertinentes queda:

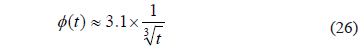
Es pertinente también calcular esta ecuación de tendencia como función de la distancia, sabiendo que U=0.119 m/s

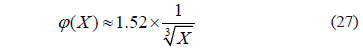
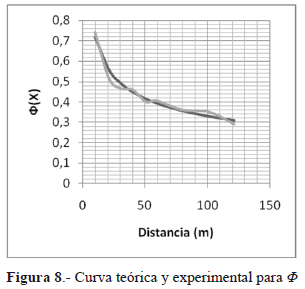
Como se puede ver en el Cuadro 1, ultima columna los datos experimentales de j se tomaron desde X=10 metros y su curva se muestra en verde en la Figura 8. La curva teórica es la calculada con la ecuación de j(X) y está en rojo.

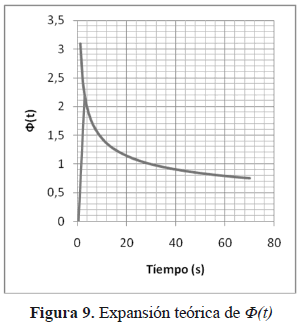
Ahora es necesario expandir a j(t) para verificar el valor pico en valores del tiempo muy cercanos al origen. Se puede ver en este caso limite que j=2.2 a un tiempo cercano a los 4 segundos. Figura 9.

 

7. VERIFICACION TERMODINAMICA DEL VALOR MAXIMO DE j PARA EL EXPERIMENTO ANTERIOR

Un dato adicional que puede dar una indicación correcta sobre la validez donde ocurre el pico de la función j se puede hacer desde la termodinámica del estado liquido considerando la definición para la "entalpia libre", DG en un proceso isotérmico e isobárico ideal como la evolución de la pluma de soluto en el flujo.[6]:

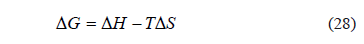
Considerando el incremento de entropía (DS) para el sistema de soluto expandiéndose isotérmicamente como un gas ideal (modelo aproximado de Van´t Hoff) [7].

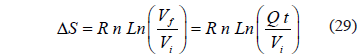
Aquí Vf y Vi son los volúmenes final e inicial del gas, R es la constante universal de los gases y n es el numero de moles del soluto. El volumen final se puede calcular por el caudal, Q multiplicado por el tiempo.

Ahora, usando la ecuación (10) para el valor pico y despejando la masa para reemplazarla en la ecuación (29)

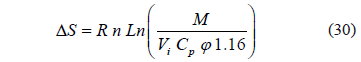
Si se considera que la masa M dividida por Vi es una concentración inicial Ci, se tiene para la ecuación (28):

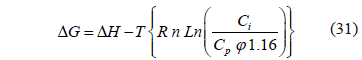
Despejando j:

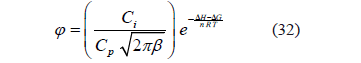
Y finalmente:

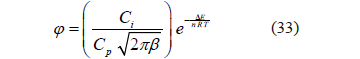
Se sabe de la teoría fisicoquímica de la materia condensada que para procesos de viscosidad del tipo Frenkel [8] como es el estudiado en este caso (y compatible con el calor de fusión para el agua) el valor absoluto de la energía DE es de entre 2.4 y 10 Kcal/mol, por lo tanto se puede verificar si en este caso la ecuación (23) es consistente con los datos numéricos.

El primer paso es calcular las concentraciones Ci y Cp de la siguiente manera:

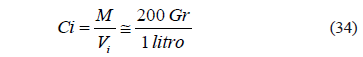
Y usando la ecuación (24) con t ≈4 seg:

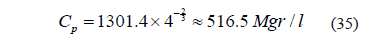
Por lo tanto:

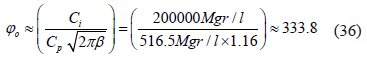
Si j=2.2, entonces la ecuación (32) queda:

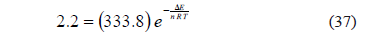
Por lo tanto:

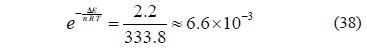
O sea, en valor absoluto:

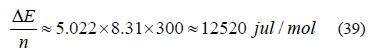
Y en calorías por mol:

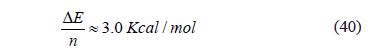
Por lo tanto el cálculo cae dentro del rango esperado y se considera que es concordante con la realidad experimental.

 

8. CONCLUSIONES

1.- Se define una función de estado, j para la evolución de la pluma de soluto en un flujo turbulento. Esta función refleja los mecanismos reales que llevan al desperdigamiento de las partículas de soluto en un líquido cortante a partir de una distribución de velocidades.

2.- Se explica cómo esta función depende de la razón de velocidades que actúan en el proceso: La velocidad de dispersión asociada a la expansión del soluto con el tiempo que tiene una naturaleza Gaussiana y la velocidad media advectiva del flujo. La primera velocidad es en realidad un mecanismo de reacción ante la ruptura del equilibrio químico y por lo tanto su comportamiento puede predecirse desde el punto de vista de cómo avanza el proceso hacia el equilibrio final. A partir de estas formulaciones se pueden conocer numéricamente los diferentes factores de la dinámica Gaussiana.

3.- Esta nueva aproximación parte de una ecuación para la velocidad media del flujo en función de la dispersión de solutos vertidos en el flujo y conduce a una expresión modificada para la función de Fick, que reproduce apropiadamente tanto la forma asimétrica como la "altura" de las curvas de concentración de trazador.

4.- A partir de una colección de ecuaciones derivadas de estos conceptos se puede aplicar esta metodología a un caso real, para etapas muy tempranas de la evolución de la pluma de soluto.

La posibilidad de adentrarse en la descripción de la nube de trazador en condiciones muy cercanas al momento de vertimiento es interesante y útil, dado que es en este tiempo en el que el impacto ambiental de los solutos es mayor.

5.-A manera de verificación, se hace un chequeo de la congruencia de dicha función por medio de la termodinámica, usando las aproximaciones de J.I. Frenkel sobre el calor de fusión para el agua. De esta forma se obtienen los datos característicos para una pequeña corriente de montaña, siendo convergentes con la expectativa teórica.

6.- A diferencia de las metodologías convencionales de interpretación del transporte de solutos tipo "zona muerta" (ADZ y TS) que agregan términos "ad-hoc" a dicha ecuación (y por lo tanto dificultan enormemente su solución analítica), esta metodología opera sobre conceptos físicos generales que son directamente tratables y congruentes con los experimentos. [9] Por lo tanto, esta metodología puede ser aplicada con gran ventaja a los estudios actuales de calidad de aguas en los cauces naturales [10], dada su naturaleza fisicoquímica clara y la sencillez de los procedimientos de cálculo propuestos.

 

RECONOCIMIENTOS

Se hace expreso reconocimiento a la Universidad de la Salle por el suministro de la información recogida por los ingenieros Pedro Villa y Andrés Bastidas de la facultad de Ingeniería ambiental de dicha universidad. Así mismo a la empresa Amazonas Technologies de Cali por el suministro de las ayudas con la tecnología Inirida Deep Flow utilizada en las mediciones. Así mismo a la agencia estatal FOMIPYME por el suministro de fondos INNOVA para el desarrollo de la tecnología.

 

REFERENCIAS

[1] Constain, A., Carvajal, J. and Carvajal, A., Frenkel´s viscosity formula recalculated through macroscopic dispersion parameters. FLUCOME, Moscow, 2007.         [ Links ]
[2] Prigogine, I. y Kondepudi, D., Modern thermodynamics. John Wiley & Sons, New York. 1998.         [ Links ]
[3] Von Mises, R., Probability, statistics and truth. Dover, USA. 1981.         [ Links ]
[4] Fischer, H.B., Report KHR-12, Caltech, USA, 1966.         [ Links ]
[5] Villa, P. y Bastidas, A., Evaluación de un método de cálculo para la "Longitud de mezcla" utilizando trazadores para su posible aplicación en estudios de calidad de aguas en ríos de montaña. [Tesis de pregrado]Universidad de la Salle, Bogotá, 2010.         [ Links ]
[6] Kikoin, I. y Kikoin, A., Física Molecular, Editorial MIR, Moscú, 1981.         [ Links ]
[7] Guaresimov, Y.A., Dreving, V., Eriomin, E., Kiseliov, A., Lebedev, V., Panchenkov, G. y Schiliguin, A., Curso de Química Física. Tomo I, Editorial MIR, Moscú, 1980.         [ Links ]
[8] Frenkel, Y., Kinetics theory of liquids. Dover, USA. 1955.         [ Links ]
[9] Constain, A. y Lemos, R., Una ecuación de velocidad media del flujo en régimen no uniforme, su relación con el fenómeno de dispersión como función del tiempo y su aplicación a los estudios de calidad de agua. Revista Ingeniería Civil No. 164, CEDEX, Madrid, 2011.         [ Links ]
[10] Montelongo, R., Gordillo, A.J., Otazo, E.M., Villagomez, J.R., Acebedo, O.A. y Prieto, F., Modelacion de la calidad del agua del Rio Tula, Estado de Hidalgo, México. Revista DYNA No. 154, pp.5-18. Medellín, 2008.         [ Links ]