MODELO ANALÍTICO PARA LA FLEXIÓN DE LA LITOSFERA: UN APROVECHAMIENTO PERTURBATIVO PARA LA RIGIDEZ FLEXURAL

ANALYTICAL MODEL FOR THE FLEXION OF THE LITHOSPHERE: AN ADVANTAGE PERTURBATIVE FOR THE FLEXURAL RIGIDITY

 

OSCAR VÁZQUEZ-RODRÍGUEZ
M. Sc. Facultad de Ingeniería, Benemérita Universidad Autónoma de Puebla, México, telaker27@gmail.com

ALEJANDRA LÓPEZ-AGUILA
M. Sc. Facultad de Ingeniería, Benemérita Universidad Autónoma de Puebla, México, mininos666@gmail.com

 

Recibido para revisar Marzo 12 de 2012, aceptado Diciembre 7 de 2012, versión final 7 de Enero de 2013

 

---

RESUMEN: Partiendo de la ecuación de Fredholm de segundo tipo, la cual modela el comportamiento de la deformación elástica de la litosfera bajo la acción de cargas verticales, se presenta una expresión analítica para la flexión de la placa litosférica en el espacio de Fourier cuando la constante de rigidez flexural se perturba por un perfil cosenoidal o, de manera general, cuando este perfil está dado por una serie de Fourier. La solución obtenida a la ecuación de Fredholm es análoga a una ecuación de recurrencia y su solución explícita a primer orden se obtiene a través de un método iterativo o perturbativo. Por último, usando nuestros resultados observamos cambios significativos en la magnitud del espectro cuando existe variación en la rigidez flexural bajo cargas ideales

PALABRAS CLAVE: Rigidez Flexural, Flexión de la Litosfera, Perturbación, Ecuación de Fredholm.

ABSTRACT: Starting from the equation of second kind of Fredholm, which models the behavior of the elastic deformation of the lithosphere under the action of vertical loads, we present an analytical expression for the deflection of the lithospheric plate in Fourier space when the constant flexural rigidity is perturbed by a cosine profile or, generally, when the profile is given by a Fourier series. The solution obtained is analogous to a recurrence relation and its explicit solution to first order is obtained via an iterative or perturbative approach. Finally, using our results we observed significant changes in the magnitude spectrum when there is variation in flexural rigidity under ideal loads.

KEYWORDS: Flexural Rigidity, Flexion of the Litosphere, Pertubation, Fredholm Equation.

---

 

1. INTRODUCCIÓN

Aplicando diversos modelos reológicos de litosfera (elástico, el viscoelástico y el elastoplástico), varios autores han podido modelar numéricamente el comportamiento flexural de ésta [1, 2, 3, 4]. Según el modelo flexural también llamado en la literatura modelo de isostasia regional, los procesos de carga litosférica tales como el emplazamiento de mantos de corrimientos, el engrosamiento cortical, la perturbación termal, sedimentación y erosión, son los principales responsables de la flexión de la litosfera en las zonas aledañas a éstos. Los diversos trabajos encaminados al estudio de la flexión en la litosfera se han dividido en el estudio de la litosfera oceánica y en la litosfera continental, en especial aplicando la teoría de elásticidad ha probado tener singular éxito en explicar arqueamientos topográficos observados en regiones sometidas a diversos regímenes de esfuerzos [2]. La flexión teórica prevista por la solución a la ecuación general flexural fue corroborada en un sinnúmero de casos geológicos. De este modo es posible explicar el arqueamiento que presenta la placa oceánica en torno a las Islas Hawai por efecto de la carga de sus islas [5]. Los estudios de flexión en la litosfera continental se iniciaron con los trabajos de Beaumont en la Cuenca de Alberta (al Oeste de Canadá) [3]. Beaumont explicó la geometría a gran escala de los sedimentos de la cuenca aplicando un modelo flexural de placa viscoelástica y simulando el emplazamiento de las Montañas Rocosas mediante cargas con forma rectangular. En los últimos años se han desarrollado estudios numéricos para modelar la flexión elástica de la litosfera usando un modelo con variación lateral del espesor elástico, donde se ha observado que estos modelos son los que más se acercan a la realidad [6, 7, 8, 9]. Debido a la dificultad que representa encontrar una solución a la ecuación flexural cuando se varia el espesor elástico, no existen soluciones analíticas. En este trabajo seguimos esta dirección y desarrollamos una solución implícita, pero analítica, cuando la variación al espesor elástico es pequeño.

Usando la ecuación general flexural para el modelo de placa elástica con variación lateral del espesor efectivo y suponiendo que los esfuerzos horizontales de la placa son despreciables, asumpcion que considera regiones tectónicamente inactivas, nosotros desarrollamos una solución implícita, en el espacio de Fourier, para la flexión de la litosfera. A partir de que la ecuación general flexural escrita en el espacio de Fourier es una ecuación de Fredholm de segundo tipo [7, 10], se propone que el espesor elástico efectivo este perturbado ligeramente por un perfil cosenoidal o en su caso más general por una función definida por los coeficientes de Fourier, y una solución explícita a primer orden se obtiene para el espectro en la flexión de la placa.

El objetivo principal de este trabajo es proveer una solución sencilla y de fácil manejo al problema de tener placas que presentan una ligera variación en su espesor elástico y así obtener resultados cualitativos y cuantitativos más cercanos a la realidad física, por consiguiente también en este trabajo presentamos una manera indirecta de medir el espesor elástico de la litosfera basado en una propuesta de Moores [11].

El desarrollo del trabajo es el siguiente, en la segunda sección se presenta la ecuación general flexural en el espacio de Fourier, y para cuando se tiene una rigidez flexural constante se define el concepto de grado de compensación. En la sección tres se desarrolla la solución implícita debida a una variación cosenoidal en el espesor de la placa o en la rigidez flexural, y bajo pequeñas perturbaciones se da una solución analítica y posteriormente esta solución se generaliza. En la sección cuatro se presenta un análisis cualitativo de nuestros resultados bajo la acción de cargas ideales. Finalmente en la última sección se resumen los objetivos y alcances del trabajo.

 

2. MARCO TEÓRICO

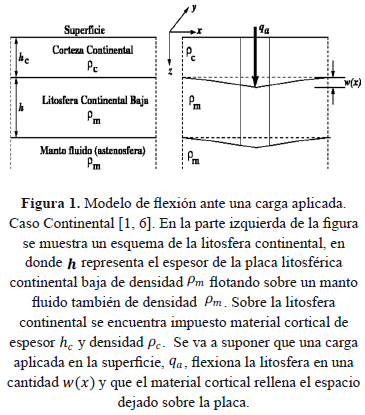
En general, la flexión de la litosfera continental puede ser explicada mediante un modelo de placa delgada, donde se supone que las cargas impuestas sobre la litosfera pueden ser parcial o totalmente soportadas por los esfuerzos elásticos de una placa litosférica (continental baja) que yace sobre una astenosfera fluida, transmitiendo lateralmente los esfuerzos generados (ver Figura 1). En este modelo flexural de placa elástica, los esfuerzos debido a la flexión se distribuyen libremente sin tener en cuenta la variación en profundidad de la resistencia de los materiales, es decir, se considera una placa homogénea.

Vamos a considerar una placa de tamaño finito, pero lo suficientemente grande para que sea más grande al espesor elástico efectivo 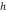de ésta, y también mayor al desplazamiento vertical 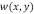que puediera sufrir en respuesta a cualquier tipo de esfuerzo. La ecuación general que relaciona el equilibrio de desplazamiento vertical 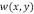de una placa elástica bajo la acción de una carga vertical 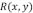queda expresada en coordenadas cartesianas ortogonales por: [6, 12].

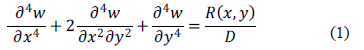
donde 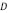es la rigidez flexural dada por:

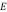La rigidez flexural indica el grado de resistencia que opone una placa de espesor , módulo de Young y razón de Poisson , a arquearse bajo la aplicación de fuerzas. Si el módulo elástico de Young es alto menos deformable resulta ser el material. Vamos a considerar que la carga aplicada sobre una placa es de densidad homogénea e isotrópica, en tal caso se verifica una equivalencia física tanto en la dirección como en la dirección , por consiguiente se puede prescindir de una de las direcciones, por lo tanto la ecuación (1) es equivalente a:

En la litosfera el campo de esfuerzos verticales está constituido básicamente por dos componentes: una carga topográfica de la corteza continental (superficie de la litosfera) 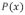dirigida hacia abajo y el empuje hidrostático 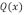dirigido hacia arriba producido por el manto líquido. En esas condiciones 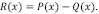Si se asume que la flexión de la placa litosférica está llenada por rocas de la corteza, la fuerza de flotabilidad ejercida por el manto puede ser expresada como el peso del manto desplazado menos el peso de las rocas de la corteza [6], es decir

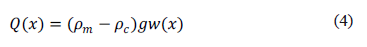
con 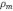es la densidad de masa del manto, 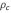es la densidad de masa de la corteza y 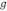es la constante de gravedad en la Tierra medida a una altitud fija. En este caso se ha asumido que la densidad de la litosfera (litosfera continental baja) es la misma que la densidad del manto (astenosfera). Usando la ecuación (4) en (3) se deriva

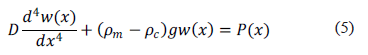
Esta es la ecuación ideal para una placa elástica delgada de espesor 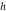la cual modela parte de la litosfera continental baja [6]. El espesor elástico 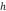no debe considerarse como el tamaño real de la litosfera continental baja, más bien se interpreta como el tamaño sobre la cual su respuesta puede estar conectada a la deformación de una placa bajo cargas.

La ecuación (5) supone que la rigidez flexural 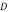es constante. Ahora vamos a suponer que la rigidez depende de la variable espacial , esto es 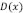. En consecuencia la ecuación (5) se ve modificada y la derivación original fue dada por Turcotte [6]:

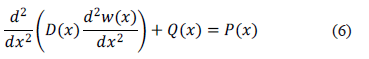
bajo las condiciones de frontera que indican la finitud de la flexión de la placa:

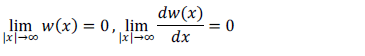
Usando la Transformada de Fourier:

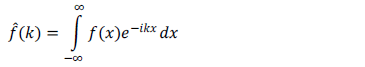
y su inversa

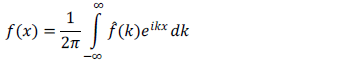
podemos rescribir la ecuación (6) al espacio de Fourier. A la variable se le conoce como el número de onda del espectro de Fourier 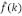asociado a la función 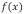. Primero, de la relación (5) usamos la inversa de Fourier para 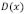y , y después de derivar se obtiene:

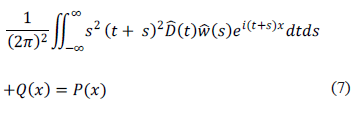
Aplicando la transformada de Fourier a la expresión (7) y usando la definición de la distribución de dirac:

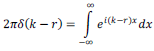, y posteriormente integrando sobre la variable se llega a

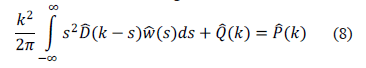
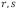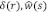La relación anterior es llamada la ecuación de Fredholm de segundo tipo [10]. Las variables y son números de onda relacionados con sus respectivos espectros de Fourier de y 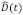, respectivamente. Cuando 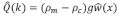entonces la ecuación de Fredholm modela la flexión de la litosfera con rigidez flexural variable [7].

Si 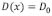, es decir el caso expresado en la ecuación (5), entonces la transformada de Fourier para esa constante es: 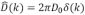, la cual sustituida en la ecuación (8) y aplicando las propiedades de la delta de dirac se llega al siguiente resultado [6, 7]:

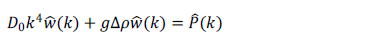
Donde 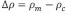, resolviendo para el espectro de desplazamiento 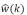se llega a:

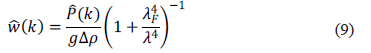
donde el número de onda 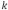se relaciona con la longitud de onda a través y es una longitud de onda característica de la placa litosférica y se define como:

En el límite de longitudes de onda larga o número de onda corta la ecuación (9) tiende a

que es equivalente a: , esto quiere decir que existe un equilibrio hidrostático entre la topografía de la corteza y el manto, dicho equilibrio representa el concepto de isostasia regional (análogo al principio de Arquímedes) en donde el manto, de mayor densidad que el material cortical, realiza una fuerza de empuje que equilibra la fuerza gravitatoria de la corteza [14]. Esto significa que el peso adicional del material cortical es igual al peso desplazado en el manto, por consiguiente existe una mayor flexión de la litosfera de lo que se daría en caso de no existir un equilibrio hidrostático. A la condición de cuando existe un equilibrio hidrostático se le llama compensación isostática y su contraparte se llama condición elásticamente soportada. 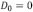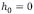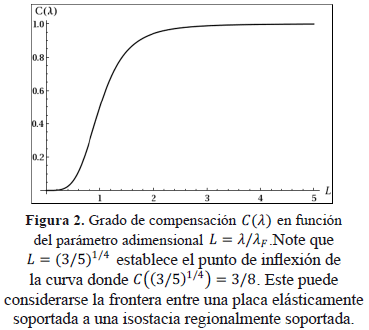Note también que la ecuación (11) se cumple también cuando , es decir cuando se cosidera que el espesor de la placa , en estas condiciones cualquier longitud de onda es mayor a la longitud de onda característica 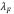, en esta situación se tiene un comportamiento de isostasia local [14]. En tal camino se puede definir el grado de compensación como la cantidad [11].

La gráfica del grado de compensación se muestra en la Figura 2, donde se ha elegido a 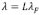, con una cantidad adimensional. De la Figura 2 se puede observar que el grado de compensación va desde para hasta para , lo cual representa el comportamiento entre una placa elásticamente soportada a una isostáticamente compensada, respectivamente. Es claro que para un perfil de carga podemos definir entonces una longitud de onda característica que separa estos dos comportamientos correspondiente a un valor de , por consiguiente si (ver Figura 2) estaremos en la frontera de un comportamiento (elástico) parcial o completamente soportado. Entonces usando la ecuación (12) y las ecuaciones (2) y (10), el espesor elástico de la litosfera está dado como [11]:

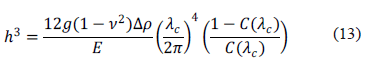
Así, el problema original de encontrar directamente el espesor elástico ha sido reducido a determinar la longitud de oda característica bajo cargas impuestas sobre la litosfera. Analizando la expresión (13) vemos que un valor grande genera un espesor efectivo pequeño y entonces será menor la carga que soporte sin que ésta sufra flexión. De manera contraria ocurre para un valor pequeño en C(l_c).

 

3. PERTURBACIÓN A LA RIGIDEZ FLEXURAL

Vamos ahora a considerar que el espesor de la litosfera varia ligeramente respecto de su valor constante, esto es equivalente a considerar que existe una variación respecto de la Rigidez flexural:

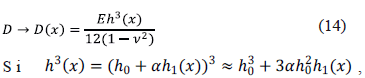
donde 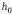es una constante asociada la rigidez flexural 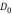. Entonces la última expresión se escribe como

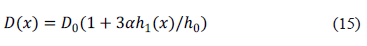
donde 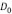es el caso dado por la ecuación (5). Si consideramos que el perfil de la altura es del tipo cosenoidal:

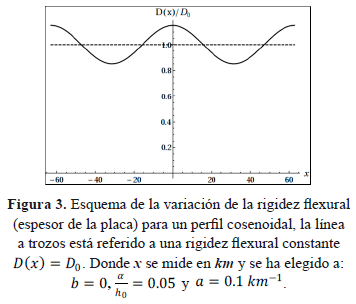
Entonces notamos que el parámetro α debe cumplir la siguiente condición 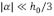. La gráfica de la ec. (15) con el perfil (16) se presenta en la Figura 3, donde se ha elegido un periodo de onda grande .

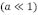Retomando la ecuación de Fredholm para el modelo litosférico.

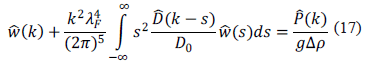
la cual se ha rescrito de manera conveniente. Ahora la rigidez flexural dada en (15), y con el perfil (16), se escribe en el espacio de Fourier como:

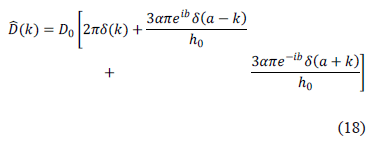
Sustituyendo esta última expresión en (17) y aplicando las propiedades de la delta de dirac en las integrales correspondientes se llega al siguiente resultado analítico para el modelo de flexión de la litosfera con rigidez flexural representado por un perfil cosenoidal:

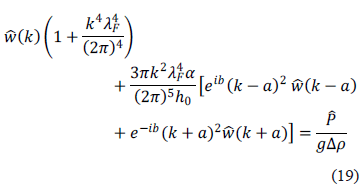
La ecuación anterior es una solución implícita para el espectro 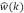y es análoga a una relación de recurrencia, notemos que para longitudes de onda larga 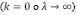se recupera el caso isostáticamente compensado (ver ecuación (11)), y en el caso de longitudes de onda corta 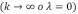se cumple que .

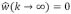La expresión (19) puede resolverse de manera iterativa, si hacemos:

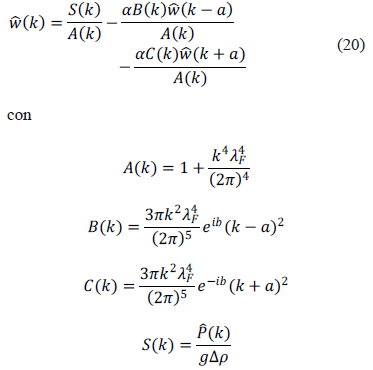
en una primera iteración se tiene

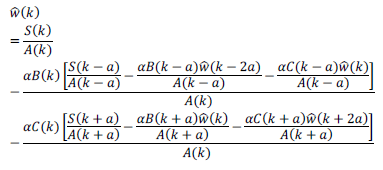
Nosotros observamos que en una segunda iteración, al resolver para 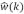y conservando términos lineales respecto a la amplitud α se llega a una solución analítica para el espectro en la flexión litosférica

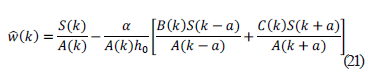
Esta misma solución se obtiene al aplicar un método perturbativo a orden lineal respecto a la cantidad 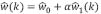, la cual se obtiene sustituyendo esto último en la expresión (20) e igualando términos semejantes, se encuentra que 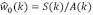el cual corresponde a una rigidez flexural constante.

La intención de resolver la ecuación espectral (19) iterativamente es debido a que si uno elige el perfil cosenoidal en el tamaño de la placa sin truncar la serie de potencias

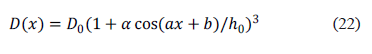
todavía existe una solución implícita para la ecuación de Fredholm (ver (17)), y tal solución está dada por

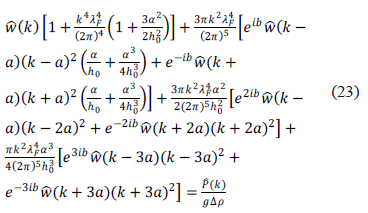
la cual se puede resolver de manera iterativa. Sin embargo el propósito de este trabajo es proveer una solución sencilla para el espectro de Fourier de 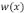y, al igual que el caso de una rigidez flexural constante [5, 6, 11, 15], proporcionar resultados cualitativos fáciles de manipular. Con esta intención nosotros hemos considerado que idealmente el tamaño de la placa sea modelada por una función sinusoidal, donde al considerar amplitudes y periodos pequeños el pérfil del tamaño de la placa se ve modificada ligeramente respecto a un tamaño constante, la cual creemos creemos que esto se ajusta más a un espesor verdadero, tomando en cuenta que las estimaciones "reales" del espesor litosférico tienen un error hasta de 20% [9]. Con esta idea vamos ahora a considerar que la perturbación 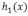está representada, en general, por una serie de Fourier, siempre y cuando 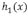cumpla con:

entonces la serie de Fourier de 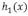es [13]

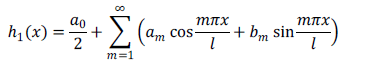
con periodo , donde los coeficientes de Fourier 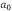, 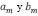se encuentran de acuerdo al método de análisis de Fourier [13]. En este caso la transformada de Fourier de la rigidez flexural dada en (15) está dada como

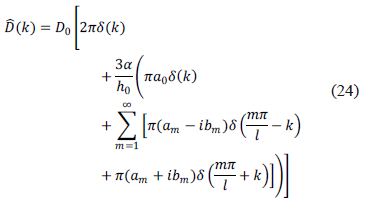
Por consiguiente la solución explícita para el espectro 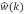es similar a la ecuación (21):

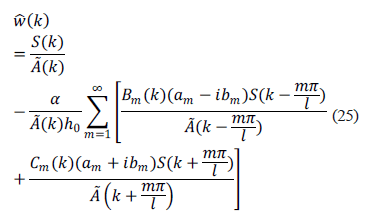
donde los coeficientes dados en la expresión anterior son iguales a los dados en la ecuación (20) con 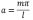y 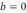. Además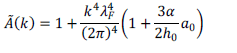

 

4. A MANERA DE EJEMPLO: PERFIL TOPOGRÁFICO IDEAL

En esta sección nos enfocamos en la deformación elástica de la placa litosférica en respuesta a una carga periodica ideal de la topografía del terreno, y vamos a comparar como se comporta el modelo no perturbado respecto al modelo perturbado. Es importante señalar que el propósito de esta sección es a un nivel de análisis cualitativo. Un trabajo con información real requiere desarrollar el análisis espectral sobre el terreno y sobre los mapas de gravedad, para esto último se necesita que las mediciones de la gravedad, y sus respectivas anomalias, se hagan a una altitud constante, esto es comúnmente llamado anomalias de la gravedad al "aire libre", otro camino que se sigue, y el más usado, para realizar las mediciones en la gravedad es referido a la anomalías de Bouguer [9, 11, 15].

Supongamos que el perfil de una carga de terreno a una altura está dada como

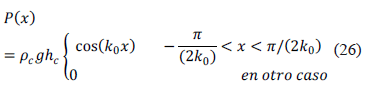
donde se ha supuesto que la densidad del terreno es igual a la densidad de la corteza y 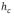es la altura máxima del terreno, aquí 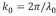, con 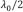es el ancho de la carga. La representación en el espacio de Fourier de la ecuación (26) está dada como

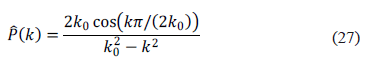
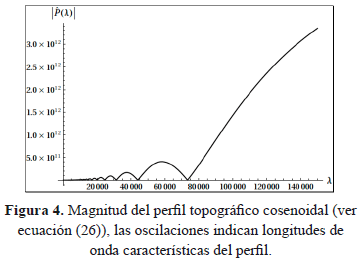
La gráfica de la magnitud del perfil de carga topografica contra una longitud de onda λ está dada en la Figura 4, donde se ha supuesto valores típicos para los parámetros de la ecuación (27), por ejemplo [6], 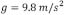,,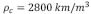 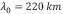y 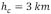. Debido a la simetría del perfil expresado en (26), el ancho de la carga es de 55 km y por consiguiente de la Figura 4 se observan oscilaciones hasta longitudes de onda de 70 km, de hecho la última longitud de onda característica (máximo en la gráfica) está alrededor de 60 km.

Primero vamos a suponer que la rigidez flexural es constante, entonces de la relación (27) y de la ecuación (9) nosotros obtenemos que la magnitud espectral de la flexión está dada como.

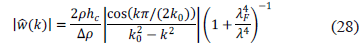
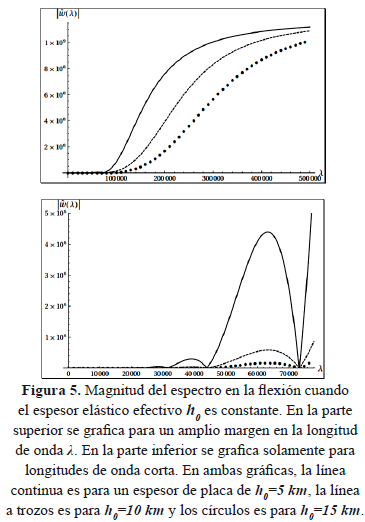
En la Figura 5 se presenta la magnitud espectral de la flexión, 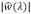, donde se ha graficado para tres diferentes magnitudes en el espesor de la placa: 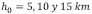y se ha usado valores típicos de las constantes físicas [6]: 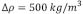, , 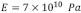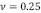. En la parte superior de la Figura 5 se observa un comportamiento análogo a la Figura 2, notando que cuando el espesor de la placa aumenta también aumenta el punto de inflexión, es decir la longitud de onda 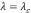que separa el comportamiento de una placa elásticamente soportada a una placa isostáticamente compensada, esto como una consecuencia de que también se incrementa el valor de 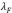. Físicamente significa que la respuesta de la placa es más sensible a espesores pequeños, es decir soporta menos carga a menor espesor. En la parte inferior de la Figura 5 se gráfica el espectro 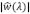pero a longitudes de onda más pequeñas, en el regímen de un comportamiento elásticamente soportado, de esa figura se aprecia que para cualquier espesor los máximos de esas oscilaciones están asociadas con las ondas características del perfil topografico, de esas oscilaciones, observamos que la máxima amplitud en el espectro se da para espesores pequeños (linea continua) indicando una mayor sensibilidad a la carga contrario a lo que sucede cuando se aumenta el espesor de la placa, esto último significa una menor flexión de la placa. A longitudes de onda más grandes, alrededor de 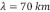, la flexión de la placa se comporta parcialmente soportada puesto que la magnitud en el espectro crece, a longitudes más grandes observaríamos un comportamiento isostáticamente compensado (ver parte superior de la Figura 5).

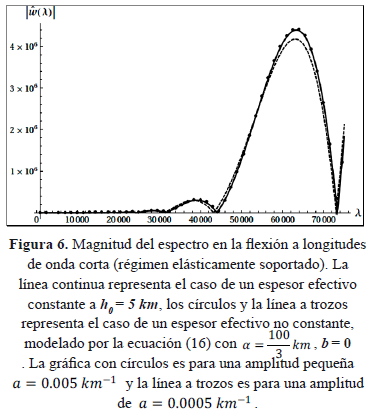
Ahora vamos a modelar la ecuación (21) para el mismo perfil dado en la relación (27), por sencillez vamos a tomar el ángulo de fase b=0. En la Figura 6 se presenta la comparación del espectro para un espesor constante h0=5 km (línea negra en la figura) y una variación en el espesor dado por los parámetros de la ecuación (16) donde se ha usado una amplitud y periodo pequeños (círculos en la figura): α=100/3 y 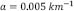. Como se puede observar en la Figura 6 no hay un cambio significativo entre un perfil constante y uno perturbado, pues al considerar amplitudes pequeñas y un número grande de oscilaciones, en promedio da como resultado un espesor constante. Sin embargo al considerar periodos más grandes (linea cortada en la figura): 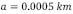, es decir menos oscilaciones, se presenta un cambio tanto en la amplitud del espectro como en un desfasamiento de la función con respecto al comportamiento de un espesor constante.

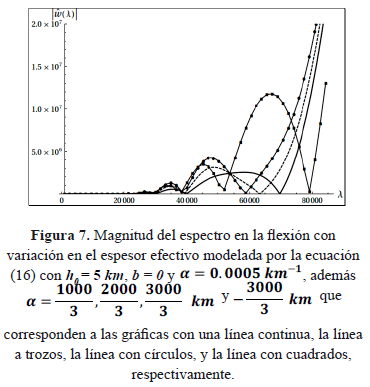
En la Figura 7, se presenta el comportamiento de la magnitud del espectro flexural a pequeñas longitudes de onda λ, con un espesor modelado por la relación (16) y considerando menos oscilaciones, es decir con un periodo grande 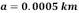, y con una amplitud en el tamaño del espesor de: 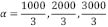y 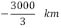(ver figura).

De esa figura observamos cambios significativos tanto en la magnitud como en el tamaño de las oscilaciones, al igual que el caso analizado de un espesor constante, magnitudes grandes en los máximos de esa figura significa que en ese intervalo el espesor de la placa es menor respecto de los otros máximos, y un mayor ancho en las oscilaciones de esa figura indica que la placa presenta una respuesta con mayor ancho en la longitud de onda.

 

5. CONCLUSIONES

En este trabajo se ha mostrado que al variar ligeramente el tamaño del espesor efectivo de la placa litosférica existe cambios significativos en el espectro flexural con respecto al modelo de un espesor constante, creemos que nuestros resultados analíticos de variar la rigidez flexural o el espesor efectivo de la placa, a pesar de que es un modelo ideal, puede proveer resultados más alentadores y cercanos a la realidad, pues si se incorpora el análisis real de los mapas topográficos (incluidas las anomalías de Bouguer) en la expresión (21) y ajustando los parámetros de la ecuación (16), se pueden obtener resultados análogos a los trabajos reportados por Moores y Andrés Tassara; o de manera más general se puede hacer el ajuste dado por la expresión (23) o (25). Finalmente, como una extensión al trabajo aquí propuesto, se puede incluir en el modelo de la flexión de la litosfera la componente correspondiente a los esfuerzos horizontales, para tomar en cuenta regiones tectónicamente activas e incorporar análisis de regiones sísmicas [16].

 

REFERENCIAS

[1] Vening-Meinesz, F. A., Gravityover the Hawaiian Archipielago and over Medeira área, Proc Netherlands Acad., Vol. 44, Wentesia, 1941.         [ Links ]
[2] Walcott, R. I., Flexural rigidity, thickness, and viscosity of lithosphere, Journal of Geophysical Research, Vol. 75, (20), pp. 3941-3954, 1970.         [ Links ]
[3] Beaumont, C., Foreland Basins, Geophys, J. R. astr. Soc., Vol. 65, pp. 291-329, 1981.         [ Links ]
[4] Fleming, P. B. and Jordan E., A synthetic stratigraphic model of foreland basin development, Journal of Geophysical Research, Vol. 94, (B4), pp. 3851-3866, 1989.         [ Links ]
[5] Walcott, R. I., Flexure of the lithosphere at Hawai, Tectonophysics, Vol. 9, pp. 435-446, 1970.         [ Links ]
[6] Turcotte D. and Shubert, G., Geodynamics. Application of continuum physics to geological problem, John Wiley, New York, 1982.         [ Links ]
[7] Sandwell, Thermomechaical evolution of oceanic fracture zone, Journal of Geophysical Research, Vol. 89, pp. 11401-11413, 1984.         [ Links ]
[8] Garcia-Castellanos, D., Fernández, M. and Torne, M., Numerical modelling of foreland basin formation: a program relating thrusting, flexure and sediment geometry and lithosphere rheology, Computers & Geosciences, Vol. 23, (9), pp. 993-1003, 1997.         [ Links ]
[9] Tassara, A. y Yáñez, G., Relación entre el espesor elástico de la litosfera y la segmentación tectónica del margen andino (15-47°S), Rev. geol. Chile, Vol. 30, (2), pp. 159-186, 2003.         [ Links ]
[10] Krasnov, M., Kiseliov, A. y Makarenko, G., Ecuaciones integrales, Editorial Mir, Moscu, 1977.         [ Links ]
[11] Moores John, and Bailey, R., Determination of the effective elastic thickness of the crust by spectral analysis. Available: www.lpl.arizona.edu/~jmoores/ElasticThickness.ppd [2003]         [ Links ].
[12] Germain, S., Examen des principes qui peuvent conduire à la connaissance des lois de l 'équilibre et du mouvement des solides élastiques, Annales de Chimie et de Physique, Tome XXXVII, pp. 337, 1828.         [ Links ]
[13] Hwe P. Hsu, Análisis de Fourier, Fondo Educativo Interamericano, México, 1973.         [ Links ]
[14] Watts, A. B., Isostasy and Flexure of the Lithosphere, Cambridge University Press, 2001.         [ Links ]
[15] Manea Marina, C. Manea Vlad, Kostoglodov Vladimir, and Guzman-Speziale Marco, Elastic thickness of the oceanic lithosphere beneath Tehuantepec ridge, Geofísica Internacional, Vol. 44, (2), pp. 157-168, 2005.         [ Links ]
[16] Otálvaro, I. y Nanclares, F., Evaluación de la respuesta dinámica de sitio para el sector de Aragón en Medellín, Dyna, Vol. 75 (156), pp. 147-155, 2008.         [ Links ]