Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.179 Medellín maio/jun. 2013
MÉTRICAS DE SIMILITUD APLICADAS PARA ANÁLISIS DE IMÁGENES DE FOTOELASTICIDAD
SIMILARITY METRICS APPLIED TO IMAGE ANALYSIS OF PHOTOELASTICITY
JUAN C. BRIÑEZ DE LEON
Estudiante Maestría Automatización y Control Industrial, ITM, juanbrinez@gmail.com
ALEJANDRO RESTREPO MARTÍNEZ
PhD. en Ing. de Sistemas, Grupo Automática y Electrónica, ITM, alejandromartinez@itm.edu.com
FRANCISCO E. LÓPEZ GIRALDO
PhD. en Física, Grupo Automática y Electrónica ITM, franciscolopez@itm.edu.co
Recibido para revisar Mayo 23 de 2012, aceptado Marzo 14 de 2013, versión final Abril 1 de 2013
RESUMEN: La mayoría de los trabajos realizados en el campo de la fotoelasticidad se han centrado en el estudio de la distribución de esfuerzos en materiales birrefringentes de espesor definido debido a la complejidad que presenta la relación entre el espesor del material, los índices de refracción y el retardo de fase que se genera en la transmisión de la luz. Existen casos donde la relación antes mencionada presenta cambios en la medida que se aplica fuerza al material en estudio, casos donde realizar una descripción del fenómeno fotoelástico es de mayor dificultad por la complejidad del mismo; la deformación de películas plásticas es uno de estos casos. Este trabajo presenta una técnica basada en métricas de similitud para el análisis de las imágenes obtenidas en estudios de fotoelasticidad de películas plásticas sometidas a deformación por esfuerzos mecánicos. La película plástica es deformada en una máquina de tracción mecánica, las imágenes de fotoelasticidad son capturadas en una cámara de vídeo a través de un montaje óptico. Los resultados del comportamiento mecánico de la deformación del material plástico presentan una dinámica que puede ser relacionada con la dinámica obtenida en las métricas de similitud.
PALABRAS CLAVE: Películas plásticas, deformación, fotoelasticidad, métricas de similitud.
ABSTRACT: Most of the works in the photoelasticity field have been focused on the stress distribution study for birefringent materials of a defined thickness, due to the complexity in the relationship between the material thickness, the refractive indices and the phase delay generated in the transmission of light. There are cases where occur temporal change on the relationship presented above while the force is applied, cases where a make a description of the photoelasticity phenomenon is more difficult by the complexity of it, the deformation of plastic films is one of these cases. This paper presents a technique based in similarity metrics for the image analysis on photoelasticity studies of plastic film deformation under mechanical stress. The plastic film is deformed in a mechanical traction machine, the photoelasticity images are captured in a video camera through of optical assembly. The dynamic behavior of the mechanical deformation in the plastic film can be related whit dynamics behavior obtained in the similarity metrics.
KEYWORDS: Plastic film, deformation, photoelasticity, similarity metric.
1. INTRODUCCIÓN
Los estudios de fotoelasticidad han pasado de técnicas soportadas en cálculos manuales a técnicas semiautomáticas basadas fotoelasticidad digital. El estudio fotoelástico esta soportado en el efecto óptico que crea el paso de luz polarizada a través de un material birrefringente, este efecto depende del retardo de fase entre los dos rayos que se producen al interior del material , el espesor del material y los índices de refracción asociados a los dos ejes de esfuerzos principales [1, 2]. En (1) se presenta la relación entre el retardo de fase, el espesor y los índices de refracción.

Donde 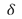 es la diferencia de fase o retardo, h es el espesor del material, n1 y n2 son los índices de refracción en los ejes principales [1, 2, 3]. En un análisis de tensión óptico bidimensional para determinación de esfuerzos es posible relacionar la expresión (1) con las direcciones principales de los esfuerzos mecánicos en el material birrefringente, como se presenta en la expresión (2).
es la diferencia de fase o retardo, h es el espesor del material, n1 y n2 son los índices de refracción en los ejes principales [1, 2, 3]. En un análisis de tensión óptico bidimensional para determinación de esfuerzos es posible relacionar la expresión (1) con las direcciones principales de los esfuerzos mecánicos en el material birrefringente, como se presenta en la expresión (2).

Donde ‘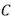 ' es el coeficiente fotoelástico del material,
' es el coeficiente fotoelástico del material, 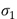 y
y 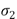 son las direcciones de los esfuerzos principales para cada dirección. Se conoce como cambio de fase relativo
son las direcciones de los esfuerzos principales para cada dirección. Se conoce como cambio de fase relativo 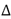 a la expresión que relaciona el retardo de fase
a la expresión que relaciona el retardo de fase 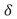 en términos de la longitud de onda. En (3) se presenta una expresión despejada para el retardo de fase
en términos de la longitud de onda. En (3) se presenta una expresión despejada para el retardo de fase 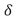 en términos del cambio de fase relativo y de la longitud de onda.
en términos del cambio de fase relativo y de la longitud de onda.

Donde D representa el cambio de fase relativo y 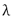 es la longitud de la onda. Al remplazar (3) en (2) y despejando
es la longitud de la onda. Al remplazar (3) en (2) y despejando 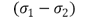 se obtiene (4):
se obtiene (4):

De (4) se extraen los parámetros para el orden de las franjas 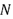 y el valor de las franjas
y el valor de las franjas 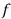 , expresándolos de la siguiente forma:
, expresándolos de la siguiente forma:
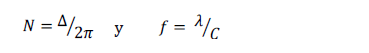
Por lo tanto la ecuación (4) se transforma en

Para la observación del fenómeno son utilizados diferentes modelos de polariscopios, la expresión para la intensidad de la luz que emerge del analizador en el caso de un modelo de polariscopio plano es [3]
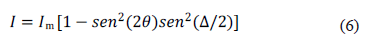
Donde Im es la intensidad de luz máxima transmitida, 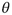 es el ángulo de configuración para los platos del polariscopio y D es la diferencia de fase que se presenta en el rayo de luz que atraviesa la muestra [1, 2, 3]. De la expresión (6) se puede decir que la intensidad de la luz que emerge del material birrefringente presenta una dependencia con la configuración de los platos del modelo de polariscopio plano y el cambio de fase relativo de los dos haces que emergen del material; el factor relacionado con el ángulo de configuración del polariscopio recibe el nombre de patrón isoclínico, y el factor relacionado con el retardo de fase recibe el nombre de patrón isocromático.
es el ángulo de configuración para los platos del polariscopio y D es la diferencia de fase que se presenta en el rayo de luz que atraviesa la muestra [1, 2, 3]. De la expresión (6) se puede decir que la intensidad de la luz que emerge del material birrefringente presenta una dependencia con la configuración de los platos del modelo de polariscopio plano y el cambio de fase relativo de los dos haces que emergen del material; el factor relacionado con el ángulo de configuración del polariscopio recibe el nombre de patrón isoclínico, y el factor relacionado con el retardo de fase recibe el nombre de patrón isocromático.
En modelos de polariscopios circulares la expresión para la intensidad de la luz que emerge del analizador se presenta en (7), tal expresión sólo está relaciona con el retardo de fase, es decir, con el patrón isocromático.

Para estudios de fotoelasticidad digital la intensidad de la luz es tomada con diferentes ángulos de configuración en los platos de un polariscopio circular, a través de cámaras o dispositivos CCD. Las imágenes obtenidas brindan información correspondiente a la intensidad de la luz que emerge del modelo óptico de polarización, técnicas para el procesamiento de imágenes son utilizadas con el objetivo de simplificar el cálculo del retardo de fase que se produce en la transmisión del rayo, también se emplea un sistema de ecuaciones obtenidas a partir del cálculo de jones que se obtiene de la configuración del polariscopio [1, 2, 3].
En trabajos recientes sobre estudios de fotoelasticidad se han desarrollado técnicas basadas en procesamiento de imágenes desde los canales de color RGB con el fin de simplificar los procesos donde se requiere del cálculo del retardo de fase; la técnica consiste en crear una tabla de calibración de colores para obtener valores del retardo a partir de la comparación de los colores [4, 5, 6].
En múltiples ocasiones en los trabajos realizados en fotoelasticidad digital asumen la intensidad de la luz como el valor del pixel en la imagen obtenida por el CCD, en [7] se propone el uso de la función de respuesta de la cámara para calibrar el valor del pixel con respecto a la intensidad de la luz que se utilizará en los cálculos del modelo fotoelástico.
La mayoría de los trabajos que se han realizado en estudio de la fotoelasticidad han estado orientados al uso de muestras de espesor constante bajo la aplicación de cargas fijas, esto se debe a la complejidad que se genera por la dependencia que existe entre espesor del material, el retardo de fase y los índices de refracción. Existen casos donde el espesor del material, los índices de refracción y el retardo de fase presentan variaciones en el tiempo, son estos casos los que motivan a implementar nuevas técnicas que permitan la descripción de este tipo de fenómenos; un caso concreto que cumple con las características anteriormente descritas es la deformación de películas plásticas termodeformables.
Las películas plásticas termodeformables experimentan el fenómeno de doble refracción óptica al ser sometidas a esfuerzos y deformaciones, tal efecto hace posible la observación de los colores de interferencia a través de la implementación de modelos de polarización utilizados en estudios de fotoelasticidad [8, 9].
En este trabajo se analizan los cambios que presentan las imágenes de una secuencia obtenida durante la deformación de películas plásticas termodeformables, a de un montaje de polarización basado en un polariscopio plano, implementado en estudios de fotoelasticidad. Los cambios en las imágenes son analizados mediante la aplicación de métricas de similitud en el análisis digital de imágenes.
El comportamiento que presentan los cambios de las imágenes a través de las métricas de similitud describe la presencia de dos zonas generales en el proceso de deformación del material plástico (Zona con cambios rápidos y zona con cambios lentos), lo cual está relacionado dinámicamente con los resultados obtenidos en las gráficas del comportamiento mecánico de la deformación.
2. MÉTODOS Y PROCEDIMIENTOS
2.1 Montaje de deformación
En trabajos realizados desde estudios de fotoelasticidad parten de la aplicación de fuerzas fijas en muestras de espesor definido [4, 5, 6], puesto que el comportamiento temporal del fenómeno óptico no es el interés de la observación; para este trabajo muestras de películas plásticas termodeformables son sometidas a deformación por tracción mecánica en la máquina de tracción Shimadzu AGX de 100KNewton, como se observa en la Figura 1.
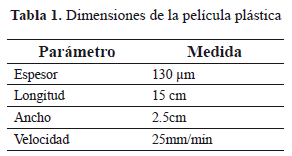
La muestra es sujetada en las mordazas de la máquina y es deformada longitudinalmente en dirección a la extrusión del material. Los parámetros de la prueba se seleccionaron siguiendo la Norma D882-10 que aplica en deformación de películas plásticas con espesor inferior a un milímetro, mediante la aplicación de fuerzas por tracción mecánica [10, 11]. En la Tabla 1 se presentan las dimensiones de la película plástica termodeformable utilizada en nuestras pruebas. El la Figura 2 se presenta un esquema de las dimensiones utilizadas.
2.2 Montaje para fotoelasticidad
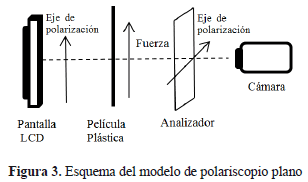
Aunque existen múltiples montajes desarrollados para estudios en fotoelasticidad [12, 13], hemos seleccionado un montaje basado en la implementación de un polariscopio plano por su simplicidad y porque nuestro interés es la observación del comportamiento de los cambios de las imágenes obtenidas a través del modelo, y no la caracterización del fenómeno a través de la medición de la intensidad de la luz y el cálculo del retardo de fase. En la Figura 3 se presenta un esquema del montaje.
Para disminuir el efecto de las franjas oscuras que hacen referencia al patrón isoclínico manipulamos la configuración angular de los polarizadores, es decir, se realizó una rotación del analizador hasta obtener un fondo oscuro con la pantalla de iluminación, el cual es conocido como configuración cruzada, donde el ángulo entre los instrumentos polarizadores es 90°. La configuración del ángulo entre los analizadores influye en la intensidad de los colores percibidos por la cámara, y por consecuencia en el análisis de las imágenes; como lo que se pretende en el trabajo es analizar los cambios en las imágenes, se debe garantizar una configuración del ángulo de polarización, que permita una adecuada observación de los colores de interferencia.
El montaje de polarización es implementado alrededor de la película plástica que es deformada en la máquina de tracción. La película es iluminada desde la cara posterior con luz polarizada transmitida de una pantalla LCD, una lámina polarizadora es ubicada en la parte frontal del material plástico con una configuración de fondo oscuro, para suplir las funciones de analizador dentro del montaje óptico, y una cámara de vídeo es utilizada para la captura de los cambios que presentan los colores de interferencia durante la deformación, del proceso se realiza un video que luego es dividido en una secuencia de imágenes.
Para la toma de imágenes se utilizó la cámara Sony Nex-3, la cual permite la grabación de vídeos a una velocidad de 30 imágenes por segundos. El enfoque de la cámara se realizó sobre la sección del material sujeto a la mordaza fija. Con el fin de controlar las condiciones de iluminación en la prueba, el lugar se iluminó sólo con la fuente de luz polarizada que produce la pantalla LCD, el resto del espacio se aisló de la entrada de luz.
2.3 Técnicas para el análisis De imágenes
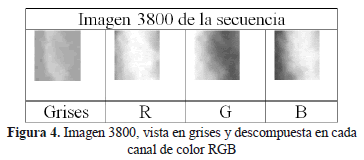
A diferencia de las técnicas aplicadas en estudios convencionales de fotoelasticidad [4, 5, 6, 12, 13] donde las imágenes son obtenidas para un mismo punto de medición con diferentes configuraciones del polariscopio y son analizadas pixel a pixel, en este trabajo se cuenta con una secuencia de imágenes para una misma configuración del polariscopio, las cuales son analizadas desde los cambios que cada una va teniendo durante el proceso. Cada imagen de la secuencia es descompuesta en cada de sus componentes del espacio de color RGB. La Figura 4 presenta un ejemplo de una imagen descompuesta en cada componente RGB.
Para describir los cambios que presentan las imágenes dentro de la secuencia obtenida durante la deformación de la película plástica, una imagen de referencia es comparada de forma ordenada con cada imagen generada dentro de la secuencia a través de la implementación de métricas de similitud; se toma como imagen de referencia la imagen inicial de la secuencia, la cual es el punto de partida en la formación de los colores de interferencia generados por la deformación del material (imagen sin cambios por la aplicación de la carga).
2.3.1 Métricas de similitud
Una métrica de similitud es una función matemática que asocia un valor numérico entre un par de descriptores, tal valor numérico es conocido con el nombre de distancia. A continuación se describen las métricas utilizadas para este trabajo.
2.3.1.1 Correlación entre imágenes
La Correlación describe el grado de dependencia lineal que existe entre una imagen y otra. El coeficiente de correlación oscila entre -1 y +1 encontrándose en medio el valor 0 que indica que no existe asociación lineal entre las dos imágenes en estudio. La expresión (8) representa la ecuación para el cálculo de esta distancia.
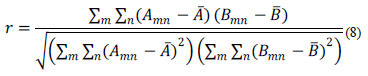
Donde A es la matriz que representa la imagen inicial y B es la matriz que representa cada imagen que se compara con la imagen inicial, 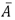 y
y 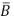 son las medias de las imágenes, n es el número de filas que contiene la imagen y m es el número de columnas que contiene la imagen [14 - 17].
son las medias de las imágenes, n es el número de filas que contiene la imagen y m es el número de columnas que contiene la imagen [14 - 17].
2.3.1.2 Distancia euclidiana para histogramas
Se utiliza con frecuencia para evaluar distancias en espacios numéricos, en este caso es utilizada para comparar los histogramas de las imágenes desde cada plano de color RGB. La expresión (9) se utiliza para el cálculo de esta distancia.
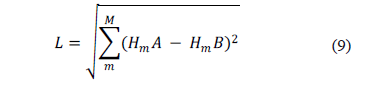
Donde 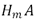 y
y 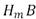 son los histogramas de las imágenes a comparar y L es el valor de la distancia euclidiana [14, 15].
son los histogramas de las imágenes a comparar y L es el valor de la distancia euclidiana [14, 15].
2.3.1.3 Correlación entre histogramas
Al igual que en la comparación entre imágenes, en este caso también describe la dependencia lineal; pero con la diferencia que ahora se aplica para comparar los histogramas de las imágenes. La expresión (10) se utiliza para el cálculo de la métrica.
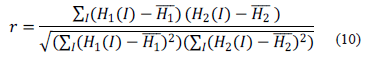
Donde 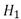 y
y 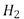 son los histogramas a comparar,
son los histogramas a comparar, 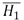 y
y 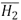 son las medias de los histogramas de las imágenes a comparar y d es el valor de la distancia [14, 15, 16]
son las medias de los histogramas de las imágenes a comparar y d es el valor de la distancia [14, 15, 16]
2.3.1.4 Distancia de Bhattacharyya para histogramas
Se utiliza para evaluar la similitud entre 2 distribuciones, el valor 1 representa la distancia mas lejana entre la distribución de los histogramas de las imágenes, el valor 0 representa la distancia mas cercana entre la distribución de los histogramas. La expresión (11) se utiliza para el cálculo de la distancia.
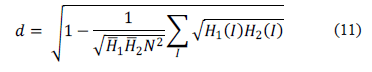
Donde 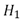 y
y 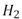 son los histogramas a comparar,
son los histogramas a comparar, 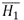 y
y 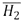 son las medias de los histogramas de las imágenes a comparar y d es el valor de la distancia [14, 15, 16]
son las medias de los histogramas de las imágenes a comparar y d es el valor de la distancia [14, 15, 16]
3. RESULTADOS Y ANÁLISIS
3.1 Comportamiento mecánico de la deformación
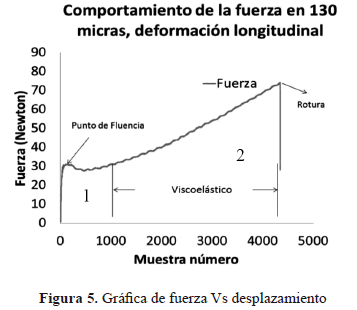
La tensión que experimenta el material plástico durante la deformación presenta cambios, los cuales están asociados al comportamiento mecánico del material, como se observa en la Figura (5); los datos de la deformación son obtenidos mediante el muestreo de la prueba realizado en la máquina de tracción. La deformación en la prueba se llevó a cabo hasta lograr la rotura de la película plástica.
La curva de la gráfica en la Figura 5 presenta un comportamiento dinámico no uniforme, la cual hemos marcado en 2 zonas, la primera zona denominada Elástico - Plástico, la cual muestra que se necesitan grandes incrementos de tensión para lograr pequeños desplazamientos en la deformación, la tensión aumenta hasta alcanzar el límite elástico de tensión (Punto de fluencia), luego decae rápidamente y empieza de nuevo el incremento. La segunda zona denominada viscoelástica presenta un incremento gradual de la fuerza hasta lograr la rotura del material plástico, esta etapa es la que mayor elongación presenta con respecto a la etapa anterior.
De la gráfica en la Figura (5) se puede observar que el comportamiento mecánico del material esta sometido a cambios rápidos en la primera etapa de la gráfica, a cambios lentos en la segunda etapa de la gráfica.
3.2 Imágenes de fotoelasticidad obtenidas en la deformación de una película plástica
La cámara del montaje óptico captura un video durante la deformación que tarda aproximadamente 3 minutos, el vídeo es descompuesto en una secuencia de imágenes para producir un aproximado de 5000 imágenes a color. Las imágenes obtenidas tienen dimensiones de 1024x576 pixeles, donde gran parte de la imagen contiene información que no es relevante para el procesamiento de ellas; por lo tanto se extrajo de cada imagen la región que contiene la información correspondiente a la película plástica, obteniendo dimensiones para las imágenes a procesar de 70x77 pixeles. La Figura 6 presenta un ejemplo de algunas imágenes extraídas de la secuencia obtenida del video de la deformación.
La imagen inicial equivale al comportamiento de la película plástica antes de empezar la deformación, las imágenes siguientes representan la deformación para diferentes instantes de tiempos en el proceso. La observación de las imágenes de la secuencia permite describir el comportamiento de los colores de interferencia durante la deformación del material plástico, se observa también que los cambios de intensidades en los colores de interferencia tienden a la formación de franjas de color, tal comportamiento puede ser comparado con el comportamiento presentado para materiales birrefringentes [5, 6].
3.3 Métricas de similitud
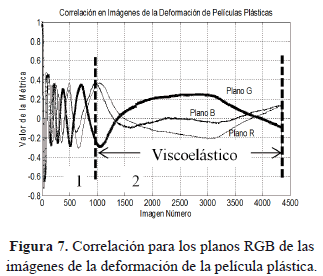
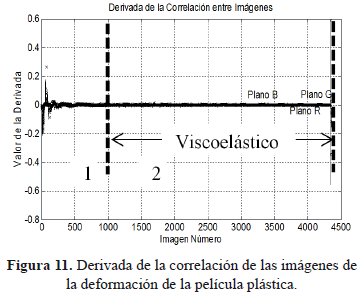
La descripción de los cambios que se observan de forma secuencial en cada imagen obtenida de la deformación de la película plástica, es realizada mediante la implementación de las métricas de similitud comparando la imagen inicial con cada imagen siguiente a través de toda la secuencia. Las gráficas para cada métrica aplicada se presentan en escala de grises, y contienen la información de los canales R, G, B. En las gráficas obtenidas para cada métrica de similitud se resaltan las etapas descritas en el comportamiento mecánico de la deformación. La Figura 7 presenta la superposición de las gráficas para la correlación entre imágenes desde cada canal de color RGB.
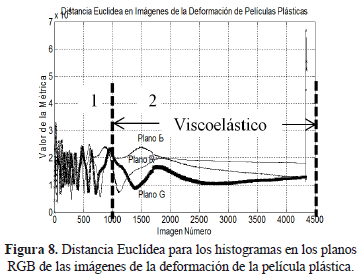
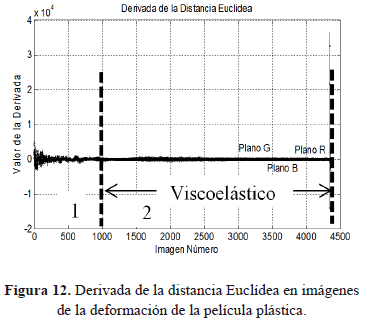
La Figura 8 presenta las gráficas obtenidas para la distancia euclidea en la comparación de los histogramas de las imágenes.
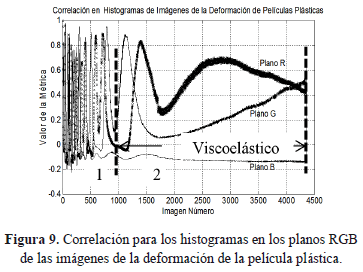
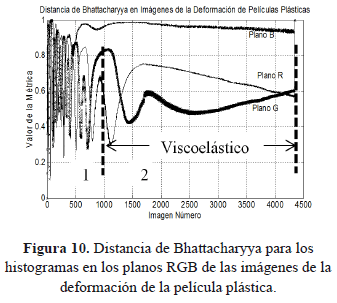
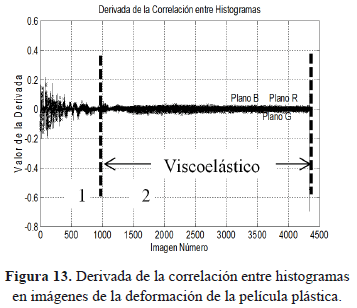
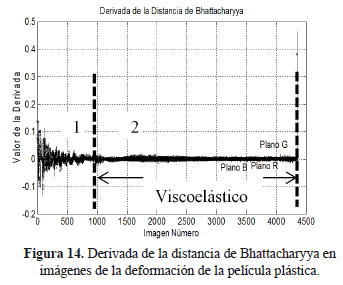
La correlación para los histogramas de las imágenes es presentada en la Figura 9, y en la Figura 10 se presenta la distancia de Bhattacharyya para la comparación de los histogramas de las imágenes.
Los cambios que se presentan en las imágenes de fotoelasticidad obtenidas en la deformación de una película plástica se pueden describir mediante métricas de similitud, estos cambios son evidenciados a través de la comparación de cada imagen con respecto a la imagen inicial.
Las gráficas de las métricas implementadas revelan que la forma como cambian las imágenes dentro de la secuencia se puede enmarcar dentro de dos zonas de comportamiento; un comportamiento inicial de cambios rápidos, donde se presentan oscilaciones en las intensidades de los colores de interferencia, y una zona de cambios lentos donde las intensidades cambian de forma gradual.
Al comparar el comportamiento de las gráficas obtenidas en las métricas de similitud, con el comportamiento mecánico de la deformación, se encuentra que la zona 1 donde la deformación pasa de una etapa elástica a una etapa plástica coincide con la zona donde los cambios que se presentan en las imágenes son rápidos; en la zona donde el comportamiento mecánico es viscoelástico, las imágenes presentan cambios lentos.
La aplicación de la derivada de las métricas implementadas para describir el comportamiento de los cambios en las imágenes permite verificar la existencia de dos zonas que caracterizan de manera general el comportamiento de las imágenes.
La Figura 11 presenta la gráfica de la derivada de la correlación entre las imágenes, en ella se observa como en la zona uno se presentan oscilaciones en la gráfica de la derivada, lo que responde a los cambios rápidos de las imágenes; la zona dos presenta pocos cambios en la derivada, lo que responde a los cambios lentos en las imágenes.
Al realizar la derivada de la distancia Euclídea aplicada a los histogramas de las imágenes se observan algunos rizos en comparación con la gráfica de la derivada de la correlación entre las imágenes, es por ello que ésta métrica permite una mejor observación al momento de identificar las dos zonas de comportamiento mecánico en la deformación de la película plástica. La Figura 12 presenta la gráfica de la derivada de la distancia Euclídea entre los histogramas de las imágenes.
La Figura 13 presenta la gráfica de la derivada para la correlación entre histogramas, se observa que en esta gráfica la presencia de oscilaciones en la zona uno al igual que en las gráficas anteriores, pero en la zona dos también se observan algunas oscilaciones que describen la presencia de algunos cambios en las imágenes dentro de la secuencia.
La derivada de la distancia de Bhattacharyya entre los histogramas de las imágenes se presenta en la Figura 14, en ella se observa una mayor amplitud en las oscilaciones de la zona uno, la cual permite identificar la presencia de cambios rápidos en las intensidades de los colores de interferencia; sin embargo aunque en la zona dos se presentan cambios graduales, se observan comportamientos que revelan la presencia de algunos cambios en las imágenes dentro de la secuencia.
Las derivadas de las métricas aplicadas presentan respuestas con dinámicas similares desde cada uno de los canales RGB, aunque la métrica muestra que los cambios no son iguales para cada canal, sobre todo para el canal G que presenta retardos con relación a los cambios en el plano R y con relación al plano B. Las zonas descritas en el comportamiento de las imágenes reflejan que el fenómeno de fotoelasticidad presenta cambios rápidos al inicio del proceso, y que cuyos cambios se hacen graduales en el resto de la deformación hasta lograr la rotura del material.
4. CONCLUSIONES
La implementación de las métricas de similitud para el análisis de imágenes permiten hacer un seguimiento del comportamiento temporal del fenómeno de fotoelasticidad experimentado por una película plástica termodeformable sometida a deformación mecánica; donde tal fenómeno está asociado al comportamiento mecánico del material.
Antes de la formación de las primeras franjas de color se observan fuertes oscilaciones en las métricas de similitud, las cuales obedecen a los cambios abruptos en las imágenes de fotoelasticidad; de lo anterior se puede inferir que las métricas de similitud permiten identificar dos grandes regiones en el proceso de deformación, la región elástica (cambios rápidos en las métricas) y la región viscoelástica (cambios lentos en las métricas).
Aunque las métricas implementadas para el análisis de las imágenes apuntan a la descripción del comportamiento temporal de los cambios en el fenómeno de fotoelasticidad, se puede decir que según los resultados obtenidos en las pruebas desarrolladas es factible resaltar a la distancia Euclidea entre los histogramas de las imágenes como la métrica que menor ambigüedad presenta, por la diferencia de rizado que se observa en la zona de cambios lentos, con respecto a las otras métricas implementadas; es por ello que la distancia Euclidea sería la métrica seleccionada para el desarrollo de una aplicación de este tipo.
REFERENCIAS
[1] Ajovalasit Augusto, Petrucci Giovanni, Scafidi Michele. Phase shifting photoelasticity in white light. Optics and Lasers in Engineering, vol 45, pp 596-611, 2007. [ Links ]
[2] Wong, C. F., Birefringence Measurement Using A Photoelastic Modulator. Applied Optics Vol. 18, (23), pp 3996-3999, 1979. [ Links ]
[3] Hillar, A. and Leo, A., Isochromatic Fringes In photoelasticity. Journal Of The Optical Society Of America A - Optics Image Science And Vision, Vol. 17 (4), pp. 750 - 755, 2000. [ Links ]
[4] Ajovalasit, A., Petrucci, G. and Scafidi. M., RGB photoelasticity applied to the analysis of membrane residual stress in glass. Measurement science and technology, vol 23, pp. 1-4, 2012. [ Links ]
[5] Azzam, R.M.A. The intertwined history of polarimetry and ellipsometry. Thin Solid Films, Volume 519, pp. 2584-2588, 2011. [ Links ]
[6] Kasimayan T. and Ramesh, K., Digital reflection photoelasticity using conventional reflection polariscope. Optics and Lasers in Engineering, vol 34, pp. 45-51, 2010. [ Links ]
[7] Shih-Hsin Chang, Hsien-Huang P. Wu. Improvement of digital photoelasticity based on camera response function. Applied Optics, vol. 50, No. 27, pp. 5263-5270, 2011. [ Links ]
[8] Restrepo. A. and López, F., Color spaces analysis of photoelasticity images of plastics thin films. Imaging and applied optics. Technical digest isbn 978-1-55752-914-5. Toronto Canada- pp. 10-14 july 2011 [ Links ]
[9] Briñez, J.C. Restrepo, A. and López F., Estudios de deformación y fotoelasticidad en películas plásticas, isbn 978-958-761-025-3, XXIV congreso nacional de física, universidad nacional, Hotel Tequendama, Bogotá, octubre 3 al 7 del 2011. [ Links ]
[10] D882-10. Standard Test Method forTensile Properties of Thin Plastic Sheeting. ASTM, marzo 28, 2011. [ Links ]
[11] D4093-95. Standard Test Method for Photoelastic Measurements of Birefringence and Residual Strains in Transparent or Translucent Plastic Materials. ASTM, marzo 28, 2011. [ Links ]
[12] Kasimayan, T., Ramesh, K., Digital reflection photoelasticity using conventional reflection polariscope. ScienceDirect, vol 34, pp. 45-51, 2010. [ Links ]
[13] Simon, B., Neethi, Kasimayan T. and Ramesh, K., The influence of ambient illumination on colour adaptation in three fringe photoelasticity. ScienceDirect, vol 46, pp.245-266, 2011. [ Links ]
[14] Wang, Z., Bovik, A. C. H. R. and Sheikh, E., Simoncelli, P., Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, vol 13, pp. pp. 600 - 612, 2004. [ Links ]
[15] R. Dosselmann, X. and Yang, A., comprehensive assessment of the structural similarity index. Signal, Image and Video Processing, vol 5, pp. 81-91, 2011. [ Links ]
[16] Maldonado, M., Sanchez, G. and Branch, J., Registration of range images using a histogram based metric. Dyna, vol 79, (176), pp. 27-34, 2012. [ Links ]
[17] Álvarez, M., González, E., Bianconi, F., Armesto, J. and Fernández, A., Características de color y textura para recuperación de imágenes en la industria del granito. Dyna, vol 77, (161), pp. 121130, 2010. [ Links ]