Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.179 Medellín maio/jun. 2013
CONTROL ACTIVO DE VIBRACIONES EN ESTRUCTURAS TIPO EDIFICIO USANDO ACTUADORES PIEZOELÉCTRICOS Y RETROALIMENTACIÓN POSITIVA DE LA ACELERACIÓN
ACTIVE VIBRATION CONTROL IN BULDING-LIKE STRUCTURES USING PIEZOELECTRIC ACTUATORS AND POSITIVE ACCELERATION FEEDBACK
MAX RIOS-GUTIERREZ
Estudiante, M.Sc., CINVESTAV-IPN, Sección de Mecatrónica, MEXICO, marios@cinvestav.mx
GERARDO SILVA-NAVARRO
Investigador Titular, Dr.Sc., CINVESTAV-IPN, Sección de Mecatrónica, MEXICO, gsilva@cinvestav.mx
Recibido para revisar Julio 9 de 2012, aceptado Abril 26 de 2013, versión final Mayo 5 de 2013
RESUMEN: Este articulo trata el problema de atenuación de vibraciones mecánicas en una estructura tipo edificio de tres niveles usando dos actuadores diferentes. El primer caso es una estructura tipo edificio con un parche piezoeléctrico como actuador en su base. El segundo caso utiliza otro tipo de actuador piezoeléctrico, en el cual sus elementos piezoeléctricos se encuentran embebidos dentro de un marco mecánico. Estos sistemas fueron modelados utilizando técnicas de análisis por elementos finitos y validados utilizando técnicas de análisis modal experimental. La ley de control utilizada para atenuar las vibraciones mecánicas, en un rango de frecuencias, está basada en la retroalimentación positiva de la aceleración y se implementa como uno o varios absorbedores pasivos virtuales sintonizados en las diferentes frecuencias resonantes del sistema. Los modelos matemáticos y el esquema de control propuesto se validan de manera experimental y se presentan resultados experimentales mostrando el desempeño dinámico en lazo cerrado.
PALABRAS CLAVE: Control activo de vibraciones, Estructura tipo edificio, Actuador piezoeléctrico, Retroalimentación positiva de aceleración.
ABSTRACT: This paper is about the suppression of mechanical vibrations in a building-like structure with two dissimilar actuators. The first case is a building like mechanical structure with a piezoelectric patch actuator on its base. For the second case the piezoelectric patch was substituted for another kind of piezoactuator, where the piezoelectric elements are enclosed in a mechanical frame. The systems were modeled using finite element analysis and validated using experimental modal analysis techniques. The control law used to properly attenuate the mechanical vibrations with excitation frequencies, in a given frequency band, is based on the Positive Acceleration Feedback, implemented with one and multiple virtual passive absorbers tuned at different vibration modes. The systems models and the proposed active vibration control scheme are validated on an experimental setup and some experimental results are presented to show the closed-loop dynamic performance.
KEYWORDS: Active vibration control, Building-like structure, Piezoelectric actuator, Positive Acceleration Feedback.
1. INTRODUCCIÓN
La supresión de vibraciones en estructuras mecánicas se ha convertido en una necesidad importante en los últimos años. El control de vibraciones en estructuras es ahora de gran interés, debido a la continua innovación en materiales inteligentes, los cuales ofrecen cada día mejores prestaciones a un precio más accesible, esto los hace de gran interés para muchas aplicaciones en ingeniería [1-6].
Una manera de suprimir las vibraciones mecánicas consiste en el uso de parches piezoeléctricos. Estos elementos están hechos de materiales inteligentes y son de creciente popularidad en ingeniería, debido a que pueden utilizarse como sensores y actuadores [7-9]. Esta característica no se encuentra en otro tipo de actuadores y también los hace convenientes para suprimir vibraciones mecánicas [7].
Es importante hacer notar que los actuadores piezoeléctricos se fabrican en muchas formas, tamaños y capacidades [7-9]. Para el trabajo reportado en este artículo se utilizaron dos tipos de actuadores piezoeléctricos, uno en forma de parche que puede cementarse, generalmente de forma permanente, en algún elemento estructural como viga, columna, etc. [10,11]. El otro actuador está basado en elementos piezoeléctricos embebidos en un marco mecánico, lo que lo hace más versátil, permitiendo distintos tipos de montaje y de forma no permanente en diferentes elementos estructurales y con mayor fuerza de bloqueo. Es conveniente señalar que los resultados experimentales obtenidos en esta estructura a pequeña escala se pueden extrapolar a sistemas más complicados y realistas desde el punto de vista de la ingeniería civil o mecánica [2,7,8].
Los modelos matemáticos de las estructuras se obtienen aplicando el método de elementos finitos, mediante la discretización de componentes mecánicos y estructuras en elementos simples como vigas, barras y placas, y resolviendo las ecuaciones lineales resultantes. Los modelos se validan comparándolos con modelos continuos clásicos, así como mediante el uso de software comercial de elementos finitos y análisis modal [12,13].
Debido a que los sistemas estudiados se actúan mediante una fuerza externa aplicada con el actuador piezoeléctrico, la dinámica en lazo abierto se modifica con la síntesis de un control por Retroalimentación Positiva de la Aceleración (PAF, por sus siglas en inglés) [14,15]. El control PAF es parte de una familia de controladores basados en la retroalimentación positiva y se emplean en el control de estructuras que pueden incluir retroalimentaciones positivas de aceleración, velocidad o posición [15]. Para la supresión o atenuación de vibraciones en sistemas mecánicos la retroalimentación de aceleración es particularmente útil porque ésta se puede obtener directamente de acelerómetros.
2. DESCRIPCIÓN DEL SISTEMA
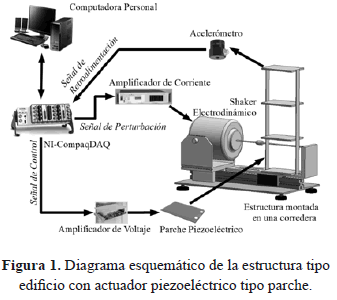
El primer sistema es una estructura tipo edificio, hecha de aluminio (Fig. 1). Esta estructura consta de diversos componentes atornillados entre sí. Dicha configuración es conveniente porque se puede extrapolar a muchos sistemas diferentes, como por ejemplo sistemas mecánicos más grandes o bien estructuras civiles.
La estructura que se utiliza tiene una altura total de 450 mm con una base rectangular de 150×100 mm. Toda la estructura está soportada por una corredera de baja fricción y la base está acoplada rígidamente a un generador electromagnético de vibraciones o shaker (modelo ET-139) fabricado por Labworks, Inc., el cual se utiliza para excitar el sistema en su totalidad con barridos frecuenciales sinusoidales hasta de 200 Hz. Este shaker se controla por su propio amplificador de potencia (modelo PA-138). Todo el sistema se conecta a una computadora personal mediante un sistema de adquisición de datos NI-CompactDAQ de National Instruments, que trabaja en la plataforma Matlab/Simulink. En la Fig. 1 se presenta un diagrama esquemático de la integración del sistema. El actuador principal de este sistema es un parche piezoeléctrico fabricado por Physik Instrumente. En este caso se utiliza el modelo P-876.A15, que está conectado a un amplificador de voltaje (modelo E-413) para manipular el parche. Este parche está cementado firmemente a una columna base de la estructura (Fig. 2), debido a que en esta parte de la estructura ocurren los esfuerzos estructurales máximos y, por consecuencia, las deformaciones normales pueden modificarse con el actuador piezoeléctrico.
Para propósitos de control la señal de aceleración se obtiene mediante un acelerómetro colocado en la parte superior de la estructura (Fig. 2). En esta planta experimental se utiliza un sistema de adquisición de datos National Instruments modelo NI-CDAQ-9172, conectado a una computadora personal con conexiones tipo USB. El sistema se controla a través de un programa en Matlab/Simulink, retroalimentando la aceleración y calculando las acciones de control para el parche piezoeléctrico. En la Fig. 2 se muestra una fotografía del sistema.
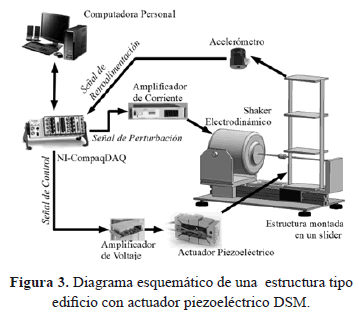
El segundo sistema es básicamente la misma plataforma experimental pero ahora utilizando un actuador piezoeléctrico modelo FPA-110 fabricado por Dynamic Structures & Materials (Figs. 3 y 4). En este actuador los elementos piezoeléctricos se encuentran embebidos en un marco mecánico y se opera mediante el amplificador de Physik Instrumente (modelo E-413).
Este tipo de actuadores piezoeléctricos tiene ventajas sobre los actuadores tipo parche, porque se pueden utilizar una y otra vez, debido a que cuentan con orificios roscados para su ensamble con tornillos a la estructura principal, sirviendo para diferentes configuraciones y tipos de estructuras. Estas características los hacen versátiles y convenientes para los propósitos de este trabajo. Estos actuadores poseen su propio marco mecánico y debido a esto la rigidez total de la estructura se afecta, ocasionando un desplazamiento en las frecuencias naturales de la estructura.
3. MODELADO DE LA ESTRUCTURA MEDIANTE ELEMENTOS FINITOS
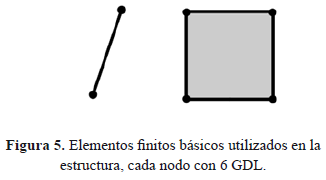
Para simular adecuadamente el sistema mecánico, la estructura se modela utilizando el método de elementos finitos. En este trabajo se aplica de manera particular el método de la rigidez directa [12]. En este método es necesario considerar dos tipos de elementos básicos: marcos espaciales, que tienen dos nodos con seis grados de libertad cada uno, y elementos tipo placa, que tienen cuatro nodos con seis grados de libertad cada uno. Una descripción de estos dos tipos de elementos básicos se muestra en la Fig. 5. Cada uno de estos elementos está asociado a una matriz elemental de masa y rigidez.
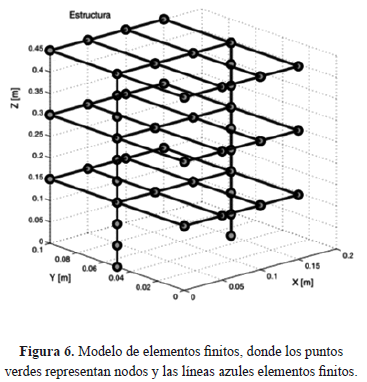
Es necesario calcular las matrices elementales, para determinar las matrices de masa y rigidez global. La estructura tipo edificio se discretiza en su totalidad con 36 elementos tipo marco espacial y 18 elementos tipo placa (Fig. 6).
Las ecuaciones de movimiento para la estructura de 324 grados de libertad, tomando en cuenta las matrices globales de masa, rigidez y amortiguamiento estructural se describen como
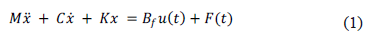
donde 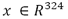 es el vector de desplazamientos nodales,
es el vector de desplazamientos nodales, 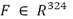 es el vector de fuerzas (vibraciones) externas,
es el vector de fuerzas (vibraciones) externas, 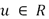 es la fuerza (momento) de control aplicada por el actuador piezoeléctrico y
es la fuerza (momento) de control aplicada por el actuador piezoeléctrico y  son las matrices de masa, amortiguamiento y rigidez, respectivamente. La representación detallada de las matrices
son las matrices de masa, amortiguamiento y rigidez, respectivamente. La representación detallada de las matrices 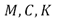 se omite por cuestiones de espacio.
se omite por cuestiones de espacio.
Para restringir el modelo de la estructura a uno más realista, es necesario aplicar las condiciones de frontera en la base de la estructura, lo cual para propósitos de simulación se realiza en Matlab (ver Fig. 6).
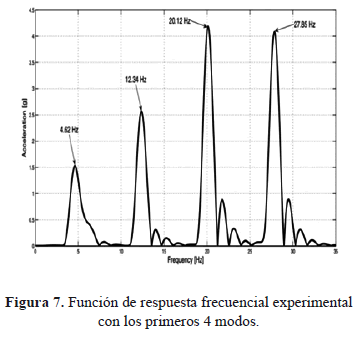
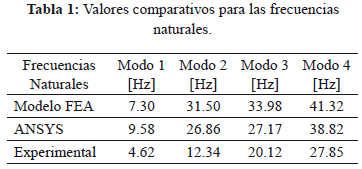
Para la validación del modelo de elementos finitos (1) se hicieron diversas pruebas experimentales con la plataforma. Durante estas pruebas se aplican fuerzas armónicas sinusoidales con frecuencia variable en un rango de frecuencias de interés, obteniendo barridos frecuenciales, a partir del acelerómetro montado en la parte superior de la estructura (ver Figs. 2 y 4). A partir de las series de tiempo se determina la función de respuesta frecuencial mediante la Transformada Rápida de Fourier (FFT, por sus siglas en inglés) tal como se ilustra en la Fig. 7. Esta caracterización experimental se hizo previo al cementado/ensamble del parche/actuador piezoeléctrico en la base de la estructura. Para validar el modelo de elementos finitos se realizaron análisis comparativos utilizando el software ANSYS y pruebas experimentales. Las frecuencias naturales resultaron similares a las encontradas con el modelo de elemento finito (1), como se describe en la Tabla 1.
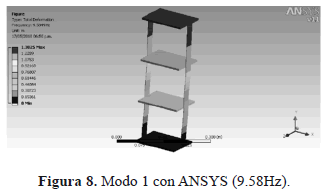
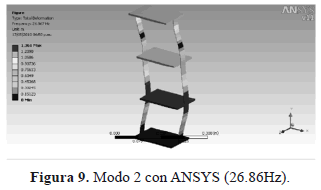
En las Figs. 8, 9, 10 y 11 se describen los primeros cuatro modos de vibración obtenidos numéricamente con ANSYS, donde se aprecia el tipo de deformación que experimenta la estructura a diferentes frecuencias naturales.
4. APLICACIÓN DE UN CONTROL POR RETROALIMENTACIÓN POSITIVA DE LA ACELERACIÓN
Para la atenuación activa de las vibraciones en la estructura mecánica se propone un control por Retroalimentación Positiva de la Aceleración (PAF). Este esquema de control es simple y tiene algunas ventajas, introduciendo un grado de libertad adicional a la totalidad del sistema y se emplea directamente la información obtenida con el acelerómetro para realizar la retroalimentación. Este controlador utiliza un tipo de absorbedor pasivo/activo virtual o filtro de segundo orden, reduce efectos indeseables y desestabilizantes en la dinámica residual y es fácil de sintonizar [14,15].
Considere la estructura mecánica de 324 grados de libertad modelada como
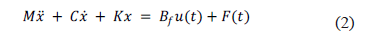
donde 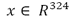 ,
, 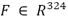 ,
, 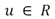 y
y 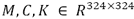 . La única fuerza de control
. La única fuerza de control 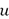 , ejercida por el parche piezoeléctrico, se utiliza para atenuar la fuerza armónica
, ejercida por el parche piezoeléctrico, se utiliza para atenuar la fuerza armónica 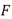 que actúa directamente sobre la estructura.
que actúa directamente sobre la estructura.
El esquema de control PAF se expresa como [15,16]
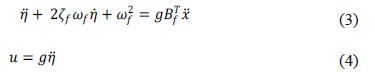
Los parámetros del control PAF (4) son la ganancia 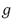 , el amortiguamiento
, el amortiguamiento 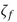 y frecuencia natural
y frecuencia natural 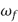 del absorbedor virtual (3). El sistema en lazo cerrado resultante es
del absorbedor virtual (3). El sistema en lazo cerrado resultante es
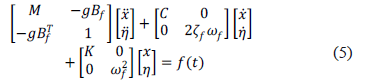
donde 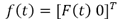 . Observe que
. Observe que 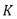 y
y 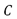 son ambas matrices simétricas y definidas positivas, lo que implica que las matrices de rigidez y amortiguamiento para el sistema en lazo cerrado son también simétricas y definidas positivas para cualquier
son ambas matrices simétricas y definidas positivas, lo que implica que las matrices de rigidez y amortiguamiento para el sistema en lazo cerrado son también simétricas y definidas positivas para cualquier 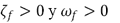 . Por otro lado, el control PAF (3)-(4) afecta únicamente la matriz de masa en lazo cerrado, es decir, Con esta matriz de masa se puede obtener la forma cuadrática
. Por otro lado, el control PAF (3)-(4) afecta únicamente la matriz de masa en lazo cerrado, es decir, Con esta matriz de masa se puede obtener la forma cuadrática
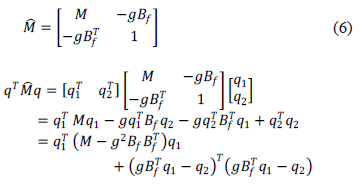
Observe que el segundo término es siempre no negativo y, consecuentemente, para garantizar la estabilidad asintótica del sistema en lazo cerrado, la matriz de masa 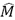 debe ser definida positiva, lo que equivale a que la ganancia
debe ser definida positiva, lo que equivale a que la ganancia 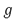 se seleccione de tal manera que la matriz
se seleccione de tal manera que la matriz 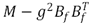 sea definida positiva.
sea definida positiva.
Para el primer sistema con parche piezoeléctrico se implementa y sintoniza un control PAF. Para lograr un desempeño satisfactorio se sintoniza el control PAF (3)-(4) para atenuar el primer modo de vibración experimental, resultando adecuados 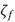 =15.9877,
=15.9877, 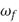 =29.03 rad/s y
=29.03 rad/s y 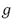 =0.5.
=0.5.
El parche piezoeléctrico se caracteriza experimentalmente con una función de transferencia identificada con el método de Peak Picking [1,13]. Específicamente, se obtiene la función de transferencia
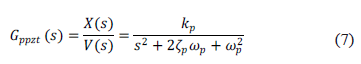
donde 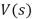 es el voltaje aplicado al actuador piezoeléctrico,
es el voltaje aplicado al actuador piezoeléctrico, 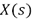 es la aceleración medida con el acelerómetro,
es la aceleración medida con el acelerómetro, 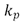 =0.5,
=0.5, 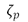 =0.5 y
=0.5 y 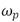 =7.3 rad/s.
=7.3 rad/s.
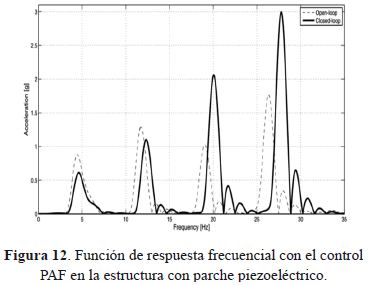
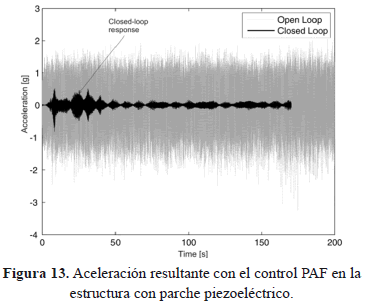
El control activo PAF se implementa en la plataforma experimental (Figs. 1 y 2). En este caso la ley de control se sintoniza para atenuar únicamente el primer modo de vibración. Se obtienen buenos resultados, como se aprecia en las Figs. 12 y 13, con funciones de respuesta frecuencial para lazo abierto y lazo cerrado, y la aceleración medida en el tercer nivel, respectivamente.
El primer modo a 4.62 Hz se reduce significativamente hasta un 30%, utilizando esfuerzos de control muy pequeños con el parche piezoeléctrico. Sin embargo, se produce el efecto conocido como roll-off (cama de agua) hacia los otros modos de vibración, desplazando las frecuencias más altas, debido a que la matriz de masa en lazo cerrado se modifica. El control PAF puede visualizarse como un absorbedor pasivo virtual que añade un grado de libertad al sistema y modifica su desempeño.
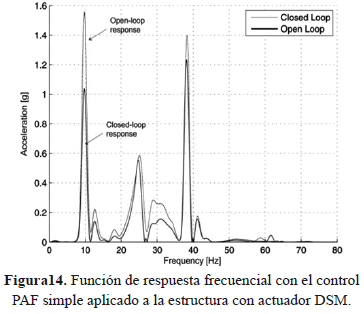
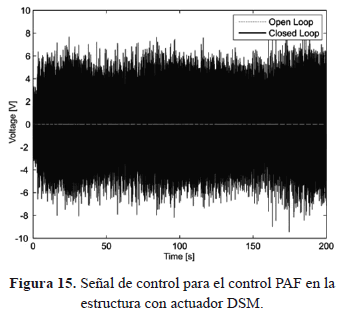
Análogamente, para el segundo sistema con actuador piezoeléctrico embebido, se aplica un control PAF para atenuar el primer modo de vibración (Figs. 14 y 15).
Los resultados experimentales muestran una reducción de hasta el 33% para el primer modo y una reducción mínima para los siguientes modos, empleando poco esfuerzo de control, como se muestra en las Figs. 14 y 15.
5. APLICACIÓN DE UN CONTROL PAF PARA LA CANCELACIÓN DE MÚLTIPLES MODOS
Con el objetivo de mejorar el desempeño en lazo cerrado con el control PAF, se consideran ahora múltiples absorbedores virtuales (filtros de segundo orden), de manera que se puedan atenuar simultáneamente varios modos de vibración [14-16]. En particular, se utilizan tres absorbedores virtuales diferentes y la fuerza de control PAF se obtiene como la suma de los efectos acoplados de estos tres sistemas.
Considere la estructura mecánica tipo edificio de tres niveles con 324 grados de libertad en la siguiente forma
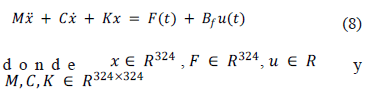
El control PAF para múltiples modos de vibración se representa como [15,16]
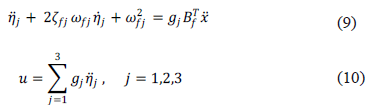
Entonces, el sistema en lazo cerrado que se obtiene es
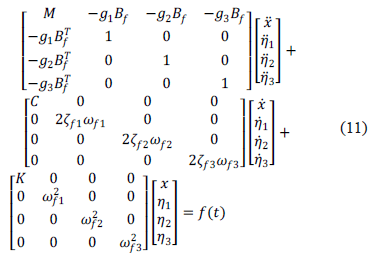
donde 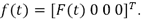 Debido a que las matrices de rigidez y amortiguamiento en lazo abierto
Debido a que las matrices de rigidez y amortiguamiento en lazo abierto 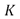 y
y 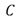 son ambas simétricas y definidas positivas, las matrices de rigidez y amortiguamiento en lazo cerrado son también simétricas y definidas positivas para cualquiera que sean los parámetros de diseño
son ambas simétricas y definidas positivas, las matrices de rigidez y amortiguamiento en lazo cerrado son también simétricas y definidas positivas para cualquiera que sean los parámetros de diseño 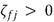 y
y 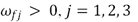 . Además, el control PAF (9)-(10) afecta únicamente la matriz de masa en lazo cerrado dada por
. Además, el control PAF (9)-(10) afecta únicamente la matriz de masa en lazo cerrado dada por
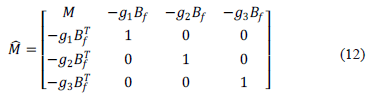
que debe ser definida positiva para garantizar la estabilidad asintótica del sistema en lazo cerrado. Entonces, los parámetros 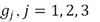 tienen que seleccionarse para garantizar esta condición.
tienen que seleccionarse para garantizar esta condición.
El control PAF (9)-(10) es capaz de atenuar simultáneamente tres modos arbitrarios de vibración y mejorar la robustez del sistema en lazo cerrado. Sin embargo, requiere de mayor esfuerzo computacional. El modelo del actuador piezoeléctrico es similar al descrito por la función de transferencia (7).
Para asegurar un desempeño adecuado aplicando el control PAF (9)-(10), se sintoniza experimentalmente para atenuar simultáneamente los primeros tres modos de vibración. Específicamente, se seleccionan 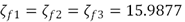 ,
, 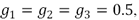
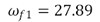 rad/s,
rad/s, 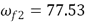 rad/s y
rad/s y 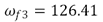 rad/s.
rad/s.
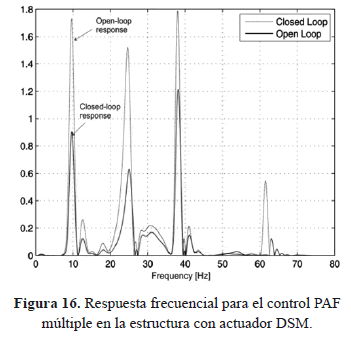
El control PAF múltiple se aplica únicamente al segundo sistema, logrando la atenuación de la respuesta vibratoria para el primer, segundo y tercer modo de vibración del 48%, 58% y 57%, respectivamente. En las Figs. 16 y 17 se muestran las respuestas frecuenciales, tanto en lazo abierto como en lazo cerrado con el control PAF, así como las acciones de control aplicadas con el actuador piezoeléctrico, las cuales se encuentran saturadas a los límites físicos del amplificador de potencia disponible.
Claramente estos resultados muestran muy buen desempeño del control PAF, en especial cuando se desean atenuar múltiples modos de vibración.
6. DISCUSIÓN
De los resultados presentados se puede concluir que el modelo matemático por elementos finitos es de suficiente precisión para alcanzar los objetivos de control para la atenuación de vibraciones mecánicas en la estructura tipo edificio de 3 niveles. Los esquemas de control basados en la retroalimentación positiva de la aceleración empleados en este trabajo muestran buen desempeño, tanto en simulación como experimentalmente.
Las estructuras mecánicas son sistemas continuos que se modelan mediante ecuaciones diferenciales parciales. Para propósitos de este trabajo y como alternativa a lo anterior, las estructuras mecánicas se modelan utilizando elementos finitos, que a pesar de la complejidad dimensional permite la síntesis de leyes de control robusto [5,6].
En particular, el modelo resultante es lineal pero con 324 grados de libertad acoplados dinámicamente. Para un modelo tan grande y complejo el control PAF es capaz de atenuar de manera eficaz la respuesta dinámica de todo el sistema, como fue el caso de los primeros 3 modos de vibración. A pesar de que el control PAF tiene un ancho de banda muy estrecho, un arreglo de múltiples absorbedores virtuales y el control PAF compuesto logran mejorar substancialmente la capacidad de atenuación de múltiples modos de vibración. Esto es evidente para el segundo sistema, donde la respuesta dinámica se atenúa hasta en 58%, donde es importante enfatizar que se alcanza una mejora en toda la respuesta dinámica del sistema, en comparación con el sistema que utiliza un parche piezoeléctrico. Por lo tanto, se confirma que el actuador piezoeléctrico embebido, aunque pequeño, es estructuralmente más conveniente para los propósitos de control en estructuras con fuerzas de magnitudes superiores.
Es importante señalar que los sistemas mecánicos pueden modelarse utilizado elementos finitos, donde se pueden implementar y sintonizar convenientemente esquemas de control PAF conforme a modelos modales obtenidos de datos puramente experimentales [7]. Por lo tanto, las técnicas de análisis modal son capaces de modelar de manera experimental casi cualquier tipo de sistema mecánico. La aplicación del análisis modal y los controladores basados en la retroalimentación positiva de aceleración o posición son alternativas muy simples y efectivas para trabajar con sistemas complejos como los encontrados en la maquinaria industrial y las estructuras civiles [15,16].
Durante el desarrollo de este trabajo se utilizaron dos diferentes actuadores piezoeléctricos de diferente forma cada uno. En ambos casos se obtuvo buen desempeño experimental.
Los parches piezoeléctricos utilizados en este trabajo tienen la ventaja de tener poca masa y entregar una fuerza considerable, además de poder cementarse en casi cualquier elemento mecánico sin mayores modificaciones estructurales, incluso en lugares donde no sería posible colocar otro actuador.
Por otra parte, el segundo tipo de actuador brinda una mejor atenuación, pero con el precio de agregar masa e introducir otras dinámicas al sistema.
Una ventaja más para utilizar actuadores piezoeléctricos es su bajo consumo de potencia, que para este caso es de alrededor de 6 W, lo cual es mínimo si se compara con la potencia consumida por un actuador electromagnético, como el usado para excitar armónicamente la estructura mecánica de 240 W.
En general, la aplicación de actuadores piezoeléctricos al problema de atenuación de vibraciones en estructuras tipo edificio a escala fue bastante satisfactorio.
7. CONCLUSIONES
El control PAF, tanto en su versión simple como en su versión múltiple, fue probado en una estructura mecánica tipo edificio de tres niveles, utilizando actuadores piezoeléctricos de dos tipos. El modelado de la estructura se obtiene por elementos finitos, resultando un sistema de 324 grados de libertad. Con este sistema se aplicaron algoritmos de control PAF, para la atenuación de uno y múltiples modos de vibración de baja frecuencia. Utilizando un control PAF simple se alcanzan atenuaciones de 30% y 33%, para cada una de las plataformas experimentales, mientras que con la utilización de un controlador PAF múltiple se obtuvieron atenuaciones de hasta 58% en tres modos. En general, la aplicación de actuadores piezoeléctricos es una opción para la atenuación de vibraciones en estructuras mecánicas utilizando esfuerzos de control y consumo de potencia muy pequeños.
REFERENCIAS
[1] Braun, S.G., Ewins, D.J. and Rao, S., Encyclopedia of Vibration. Vol. 1-3, Academic Press, San Diego, CA, 2001. [ Links ]
[2] Datta, T.K., Seismic Analysis of Structures. John Wiley & Sons, Asia, 2010. [ Links ]
[3] De Silva, C.W., Vibration: Fundamentals and Practice. CRC Press, Boca Raton, FL 2000. [ Links ]
[4] Song, T.T. and Spencer, B.F. Jr., Supplemental energy dissipation: state-of-the-art and state-of-the-practice, Engineering Structures, 24, pp. 243-259, 2002. [ Links ]
[5] Gomez, D., Marulanda, J. y Thomson, P., Sistemas de control para la protección de estructuras civiles sometidas a cargas dinámicas, Dyna, 75(155), pp. 77-89, 2008. [ Links ]
[6] Gawronski, W.K., Advanced Structural Dynamics and Active Control of Structures. Springer-Verlag, NY, 2002. [ Links ]
[7] Preumont, A., Mechatronics: Dynamics of Electromechanical and Piezoelectric Systems. Springer-Verlag, Dordrecht, 2006. [ Links ]
[8] Brennan, M.J., Garcia-Bonito, J., Elliott, S.J., David, A. and Pinnington, R.J., Experimental investigation of different actuator technologies for active vibration control, Smart Materials and Structures, 8(2), 145, 1999. [ Links ]
[9] Devasia, S., Meressi, T., Paden, B. and Bayo, E., A piezoelectric actuator design for vibration suppression: placement and sizing, J. Guidance, Control and Dynamics, 16(5), pp. 859-864, 1993. [ Links ]
[10] Rios-Gutierrez, M. and Silva-Navarro, G., Finite element and modal modeling of a cantilever beam with piezoelectric patch actuator for vibration absorption. Proc. 6th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE 2009), pp. 515-520, Toluca, México, November 2009. [ Links ]
[11] Gani, A., Salami, M.J.E. and Khan, R., Active vibration control of a beam with piezoelectric patches: real-time implementation with xPC target, Proc. IEEE Conf. on Control Applications, pp. 538-544, 2003. [ Links ]
[12] Kattan, P., Matlab Guide to Finite Elements. Springer-Verlag, Berlin, 2007. [ Links ]
[13] Ewins, D.J., Modal Testing: Theory, Practice and Applications. Research Studies Press Ltd., Baldock, UK, 2000. [ Links ]
[14] Inman, D.J., Vibration with Control. John Wiley & Sons, UK, 2006. [ Links ]
[15] Inman, D.J., Tarazaga, P. and Salehian, A., Active and passive damping of structures, Proc. 13th International Congress on Sound and Vibration, Vienna, Austria, 2006. [ Links ]
[16] Friswell, M.I. and Inman, D.J., The relation between positive position feedback and output feedback controllers, Smart Materials and Structures, pp. 285-291, 1999. [ Links ]