Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.179 Medellín maio/jun. 2013
CARACTERIZACIÓN DE PROPIEDADES MECÁNICAS MEDIANTE ANÁLISIS INVERSO DEL MÉTODO DE LOS ELEMENTOS FINITOS COMBINADO CON ENSAYO DE INDENTACIÓN
CHARACTERIZATION OF MECHANICAL PROPERTIES BY FINITE ELEMENT METHOD INVERSE ANALYSIS COMBINED WITH INDENTATION TEST
JÉSICA ISAZA
Estudiante Maestría en Ingeniería, Universidad Nacional de Colombia, jaisaza@unal.edu.co
ISABELA MARIAKA
Ing. Mecánica, Universidad Nacional de Colombia imariakaf@unal.edu.co
JUAN RAMÍREZ
Profesor Asociado Universidad Nacional de Colombia jframirp@unal.edu.co
Recibido Diciembre 3 de 2012, aceptado Abril 19 de 2013, versión final Mayo 5 de 2013.
RESUMEN: Se propone un método para establecer propiedades mecánicas de materiales mediante el uso de ensayos de indentación. El método que permite determinar parámetros constitutivos que definen la respuesta del material, consiste en combinar los resultados experimentales con un modelo numérico de elementos finitos. El primer resultado de este estudio, correspondiente a un modelo numérico simplificado en el que se asume un caucho de silicona como una única capa con un comportamiento mecánico elástico lineal e isotrópico, fue validado con resultados de propiedades mecánicas encontrados analíticamente. Este análisis será extendido para modelos biológicos multicapa más realistas en trabajos futuros.
PALABRAS CLAVE: Método de elementos finitos, análisis inverso, propiedades mecánicas, ensayo de indentación, caucho de silicona.
ABSTRACT: A method is proposed to determine the mechanical properties of materials by the use of the indentation tests. It also allows to determine the mechanical parameters that control the material mechanical response by combining experimental results with a numerical finite elements model. The first results presented in this study correspond to a simplified numerical modeling of silicone rubber. The rubber was assumed as an one-layer material with an isotropic linear elastic mechanical behavior. The method was validated analytically; and this analysis, specially the method, will be extended to biological multilayer models in further studies.
KEYWORDS: Finite element method, inverse analysis, mechanical properties, indentation test, silicone rubber.
1. INTRODUCCIÓN
Las propiedades mecánicas de los tejidos blandos son de gran interés para diferentes aplicaciones médicas, como los procedimientos de intervención con ayuda de computadora y de imágenes médicas [1]; el diagnóstico de cáncer, planeación de tratamientos [2] e imposición de realismo en simulaciones de interés médico [3].
Las pruebas in vivo, aunque permiten conocer con fidelidad el comportamiento de ciertos tejidos, son costosas y se encuentran restringidas o limitadas a pruebas no invasivas, por lo que no puede obtenerse probetas para ensayos normalizados. La experimentación para obtener propiedades mecánicas de los tejidos, permite dar continuidad al perfeccionamiento y obtención de nuevos algoritmos para el desarrollo de técnicas de imagen que relacionan la elasticidad de los tejidos, como es el caso de la elastografía e imágenes sonográficas.
La elasticidad es una propiedad mecánica que indica la capacidad del material para recuperar sus dimensiones originales después de retirar las cargas que produjeron en él determinadas deformaciones [4]. Por tanto, la forma general de medirla es cuantificar cuánto se deforma el material al aplicar una fuerza conocida o medir la fuerza que se requiere para deformarlo una distancia establecida. Para algunos materiales la respuesta a una carga aplicada es instantánea, lo que quiere decir que la deformación varía linealmente con la magnitud de la carga aplicada, conociéndose como ley de Hooke [5], cuya ecuación desarrollada por Robert Hooke, es considerada la primera ecuación constitutiva.
Las ecuaciones constitutivas [9], relacionan dos magnitudes físicas de un material para aproximar su respuesta mecánica a un estímulo determinado y aproximan su respuesta mecánica a fuerzas externas para describir los comportamientos mecánicos de los materiales. Para los demás comportamientos mecánicos no lineales existen múltiples modelos constitutivos que permiten establecer fenomenológicamente la respuesta mecánica de los materiales.
Para muchos materiales, los modelos elástico-lineales, no describen con exactitud el comportamiento mecánico del material [6], ya que presentan altas deformaciones bajo pequeñas cargas, describiendo un comportamiento no lineal. Estos materiales han sido modelados bajo condiciones de hiperelasticidad para grandes deformaciones [6] y viscoelasticidad para los materiales cuyos esfuerzos generados dependen tanto de la deformación como de la velocidad de la misma [8].
El ensayo de indentación es una herramienta que permite determinar ecuaciones constitutivas que representan propiedades mecánicas relacionadas con la elasticidad y la dureza. El análisis de los resultados y la determinación de las propiedades, se realiza considerando la relación entre la fuerza y el desplazamiento o la fuerza y el tiempo de respuesta [10]. El método propone comparar las mediciones experimentales con los resultados de una simulación que reproduce el método de medición mediante el Método de los Elementos Finitos [10] [11] [12] [13].
Caracterizar mecánicamente un material como el caucho de silicona permitirá validar el método de análisis inverso al comparar los resultados del módulo de Young óptimo usado en el modelo numérico con los resultados analíticos aplicando la teoría de Hertz. El caucho de silicona para moldes es un elastómero de silicona de dos componentes, que mezclados a temperatura ambiente reticulan, obteniendo un producto final flexible y elástico [14].
La investigación propuesta tiene como objetivo el desarrollo y validación de un método que permita establecer los factores de la ecuación constitutiva que representa las propiedades mecánicas del material, el procedimiento general puede ser aplicado para cualquier material biológico o no. El estudio combina el ensayo de indentación con una simulación numérica mediante el método de los elementos finitos, usando el software Abaqus. En trabajos futuros se realizarán pruebas para materiales biológicos y multicapa, como la piel.
2. MATERIALES Y METODOS
El análisis inverso consta de diferentes métodos: un ensayo de indentación para obtener los resultados experimentales que expresan el comportamiento del material; la simulación numérica replica las condiciones experimentales; posteriormente un algoritmo de optimización soluciona el problema inverso permitiendo encontrar una ecuación constitutiva como propiedad mecánica del modelo numérico que se ajuste a la curva experimental inicial. Finalmente, se valida el procedimiento al comparar los resultados con los hallados analíticamente.
2.1. Ensayo de Indentación
El ensayo de indentación se desarrolló en un texturómetro perteneciente a la Universidad Nacional de Colombia, descrito como un equipo que permite medir las fuerzas normales aplicadas mediante un indentador de acero inoxidable a la muestra de caucho de silicona.
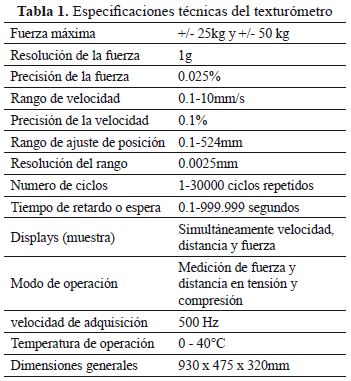
Las principales características técnicas del texturómetro son:
Una representación del dispositivo se muestra en la Figura 1, donde es posible diferenciar el equipo de indentación, el sistema de adquisición y el display de visualización.
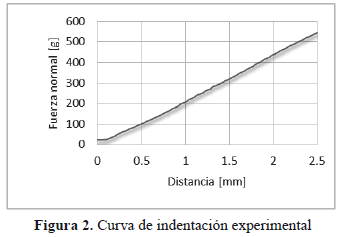
Durante la indentación, es medida la variación de la fuerza de contacto como función de la profundidad de indentación, por lo que se puede obtener una curva de desplazamiento-fuerza que posteriormente será usada en el análisis inverso. Un ejemplo de la curva correspondiente al caucho de silicona se presenta en la Figura 2.
Se realizó un diseño de experimentos para validar los resultados de la indentación e identificar si hay incidencia de algunos factores experimentales, como los que se describirán más adelante, sobre la respuesta mecánica del material.
A través de un estudio exploratorio de las variables involucradas en el proceso de indentación, se identificaron sus posibles valores, concluyéndose que las variables o factores de interés a ser analizados y sus respectivos niveles son los siguientes: Geometría del indentador: los esfuerzos concentrados pueden alterar los resultados experimentales, por lo que se consideran dos niveles, indentadores de punta plana o esférica.
Diámetro del indentador: puede afectar la respuesta mecánica al modificar el área de contacto, se varía en dos niveles: 5mm o 10mm.
Velocidad de indentación: el material puede presentar una dependencia con el tiempo, correspondiendo a un material viscoelástico, los niveles a variar son 6, 5, 25, 45, 80, 130, 180 mm/s.
Considerando que se tienen tres factores y cada uno con distintos niveles, el diseño experimental más apropiado es el diseño factorial general, requiriéndose al menos una réplica para realizar el ANOVA [15], siendo necesario realizar 48 corridas experimentales.
Considerando el diámetro mayor del indentador de 10mm y para minimizar el efecto de borde sobre la muestra de caucho al aplicar la fuerza de indentación, se fabricaron muestras paralelepípedas utilizando perfilería cuadrada de 35x35 y 30mm de alto como molde. Al emplear cada una de las caras en contacto con el perfil como superficie para realizar la indentación, se garantiza caras paralelas y perpendicularidad con el equipo de medición para evitar efectos de cuña durante la experimentación.
Al poder emplear cuatro de las seis caras del cubo, para un total de 48 corridas se fabricaron 12 muestras de caucho de silicona. La mezcla del caucho y catalizador se realizó en una proporción de 100:5 respectivamente, siguiendo las indicaciones del fabricante para el proceso de mezclado y vertido en los diferentes moldes. Después de 24 horas de secado, se procedió al desmolde y almacenamiento.
El protocolo de experimentación incluye realizar las pruebas de indentación aleatoriamente sobre cada una de las cuatro caras del cubo en contacto con la perfilería; marcando cada una de las caras a ser indentada según el orden de salida de estas del recipiente de almacenamiento; después de cada indentación se devuelve la muestra al recipiente si aún hay caras sin marcar, en caso contrario se retira definitivamente de la recipiente. Después de realizar la marca en la superficie, la muestra se ubica de forma que el indentador esté lo suficientemente cerca de la cara para iniciar el contacto y se realiza una indentación de 2.5mm de profundidad según la matriz de diseño preestablecida.
2.2. Determinación del Módulo Elástico
2.2.1. Analítico
El proceso de experimentación arroja valores de fuerza de reacción (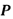 ) y profundidad de indentación (
) y profundidad de indentación (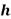 ) . Para obtener a partir de ellos un módulo de Young (
) . Para obtener a partir de ellos un módulo de Young (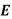 ) se emplearon las siguientes ecuaciones [12].
) se emplearon las siguientes ecuaciones [12].
Para un indentador cilíndrico de punta plana se aplica la siguiente ecuación:

Donde 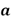 es el radio del indentador que estará en contacto; y
es el radio del indentador que estará en contacto; y 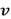 es el módulo de Poisson, para el caso de cauchos y siliconas puede asumirse como 0.4 [16].
es el módulo de Poisson, para el caso de cauchos y siliconas puede asumirse como 0.4 [16].
Para el caso del indentador cilíndrico de punta esférica se emplearon las siguientes ecuaciones:

Donde 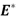 es un módulo combinado entre el material del indentador y la muestra, está dado por:
es un módulo combinado entre el material del indentador y la muestra, está dado por:
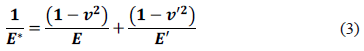
El material del indentador que se utilizó en el experimento es acero inoxidable 304 para el que se suponen 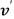 =0.33 y
=0.33 y 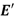 =7.4x1010Pa [17].
=7.4x1010Pa [17].
Los valores resultantes del módulo de Young de las 48 pruebas fueron tomados como variable de respuesta en el diseño del experimento.
2.2.2. Numérico
El Método de Elementos Finitos (MEF) [18] es una herramienta versátil a disposición de los investigadores para el análisis del comportamiento de materiales y estructuras sometidas a diversos estados de carga. Su mayor ventaja consiste en la posibilidad de simular de forma realista la respuesta de un sistema bajo diversos estímulos mecánicos sin tener que recurrir a métodos experimentales que pueden ser en algunos casos excesivamente costosos o incluso imposibles de realizar debido a la propia naturaleza del fenómeno estudiado.
La precisión de los resultados obtenidos con esas simulaciones está directamente relacionada con la habilidad del investigador para reproducir de una manera precisa la geometría [19], las condiciones de borde y las propiedades mecánicas del fenómeno simulado.
Se desarrolló un modelo numérico estático axisimétrico, en el que se simula el contacto entre un cuerpo rígido y uno deformable isotrópico, lineal y elástico. El modelo representa las condiciones experimentales en sus condiciones de frontera. Posterior a un análisis de convergencia se decidió trabajar con una malla construida con 1064 elementos planos 2D cuadrados, CAX4R. En la Figura 3 se muestra una malla un poco más densa hacia el centro del modelo (lateral izquierdo) y la parte superior o de contacto. Se simplificó la geometría, asumiendo que no era una muestra cúbica sino cilíndrica, para realizar el modelo axisimétrico, lo que no tiene grandes implicaciones al asumir que para tan baja indentación, teniendo en cuenta el radio del indentador, la superficie del espécimen se considera infinita y el volumen del modelo es equivalente al de la probeta real.
El coeficiente de fricción (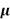 ) entre el indentador de acero inoxidable y la muestra de caucho de silicona fue medido en un equipo capaz de medir simultáneamente fuerzas tangenciales y normales, desplazando el indentador en los ejes normal y transversal para obtener el valor de la fuerza de reacción y hacer uso de la siguiente ecuación:
) entre el indentador de acero inoxidable y la muestra de caucho de silicona fue medido en un equipo capaz de medir simultáneamente fuerzas tangenciales y normales, desplazando el indentador en los ejes normal y transversal para obtener el valor de la fuerza de reacción y hacer uso de la siguiente ecuación:

Para resolver problemas que impliquen estados de esfuerzos, en general se conocen las condiciones de frontera, las propiedades del material y la geometría, y se busca obtener valores de esfuerzo-deformación (o fuerza-desplazamiento) en cualquier punto del dominio. Si se asume que no se conocen las propiedades del material, pero sí la relación fuerza-desplazamiento (obtenidas de mediciones experimentales), la geometría y las condiciones de contorno; un análisis inverso del método de elementos finitos [20] permite encontrar las propiedades del material mediante la ejecución de múltiples simulaciones enmarcadas en un proceso iterativo, hasta llegar a la óptima relación de fuerza-desplazamiento que coincide con las mediciones experimentales, como se indica en la Figura 4.
Para realizar este procedimiento, se asumió un módulo de Young inicial que caracterizara aproximadamente al caucho de silicona y se desarrolló un modelo numérico en el software comercial Abaqus, en el que se repliquen las condiciones de frontera del experimento. Luego se implementa un algoritmo de optimización en Matlab® que encuentra las diferencias (error) entre las curvas de la medición experimental y el resultado del modelo numérico y propone un nuevo valor de módulo de Young para minimizar el error entre ellas.
El algoritmo de Levenberg-Marquardt es un método iterativo de optimización aplicado para minimizar funciones generalmente no lineales [21], el algoritmo interpola entre el algoritmo de Gauss-Newton y el método de descenso de gradiente, lo que hace que la solución sea más robusta y posible de alcanzar.
El algoritmo emplea una ecuación de ajuste lineal o no lineal. Para este caso se usó una ecuación del tipo:

Donde y son constantes asumidas inicialmente y comparadas en Matlab® empleando el algoritmo de Levenberg Marquardt. Mediante la ejecución de múltiples simulaciones, hasta llegar a la óptima relación de fuerza-desplazamiento coincidente con la medición experimental se obtiene finalmente un módulo de Young.
3. RESULTADOS
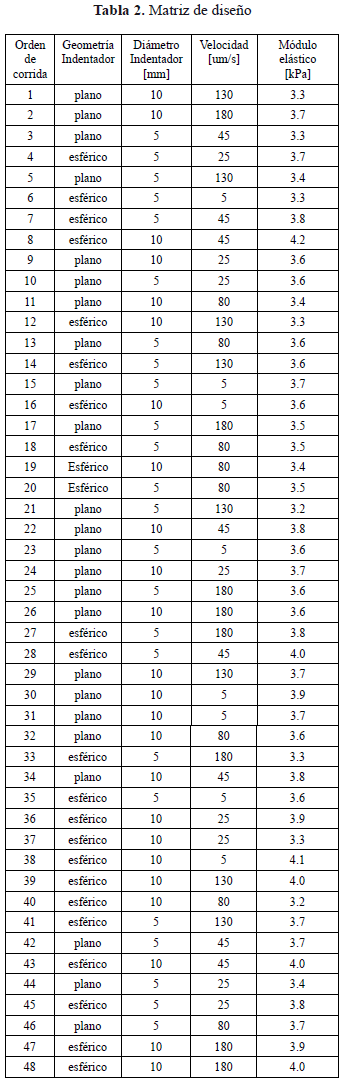
A partir de los valores de fuerza desplazamiento arrojados por el sistema de adquisición del texturómetro, se encontraron los módulos de Young para cada una de las corridas experimentales. A continuación en la Tabla 2 se presenta la matriz de diseño del experimento y los respectivos valores de módulo elástico longitudinal encontrados analíticamente mediante las ecuaciones (1) y (2) según el caso.
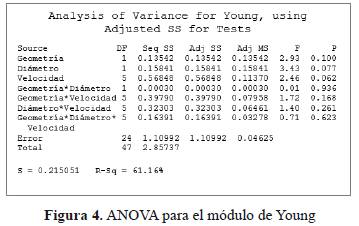
Del ANOVA realizado con Minitab® versión 16, mostrado en la Figura 4, se puede observar que ninguno de los efectos principales son significativos, ya que el p-value es mayor que 0.05 al igual que los efectos de sus respectivas interacciones dobles.
La ejecución del diseño del experimento satisface las condiciones de distribución normal de la respuesta, varianzas iguales y aleatoriedad en la toma de datos.
No hay incidencia de ninguno de los factores sobre la respuesta, es decir, no hay ningún efecto significativo resultante de la variación en la geometría o el diámetro del indentador, ni tampoco como respuesta al cambio en la velocidad de indentación. Las medias son estadísticamente iguales, obteniéndose una media del módulo de Young de 3.6kPa.
El coeficiente de fricción que se obtuvo de dos corridas experimentales empleando la ecuación (4), es de 0.21 para la primera y 0.19 para la segunda. De ahí puede considerarse un promedio de 0.2.
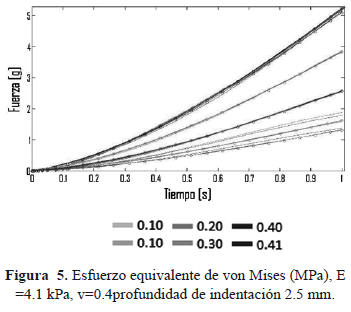
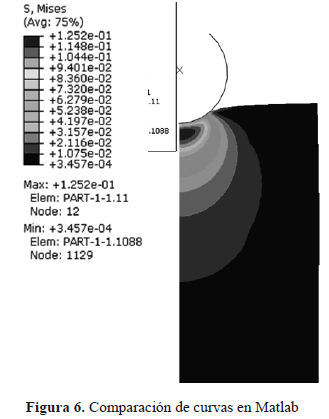
En la Figura 5 se muestra un resultado típico del modelo numérico. La sumatoria de las fuerzas de reacción de cada uno de los nodos de la base de la muestra en un instante de tiempo en el que se realiza la indentación completa; es comparada con las curvas de fuerza-tiempo obtenidas experimentalmente. La comparación final realizada en Matlab®, es mostrada en la Figura 6, en ella se visualiza el cambio de los módulos de Young en el modelo computacional para minimizar el error con la curva experimental.
Para obtener una convergencia del 95% entre las curvas, mediante comparación de las constantes y , se empleó un módulo elástico de 4.1kPa en el análisis inverso mediante el método de los elementos finitos.
4. DISCUSION
Dado que no se encontró en la literatura ningún valor de módulo elástico para el caucho de silicona con estas características de mezcla, se comparó el valor encontrado analítica y numéricamente con el resultado de un ensayo de compresión, llevado a cabo en el mismo equipo, que arrojó un módulo de Young de 3.8kPa. Al comparar este valor con 4.1kPa encontrado en el análisis inverso y 3.6kPa como resultado analítico; puede considerarse que no hay diferencias significativas, por lo que pueden emplearse cualquiera de los dos métodos para hallar el módulo de Young en materiales elásticos lineales.
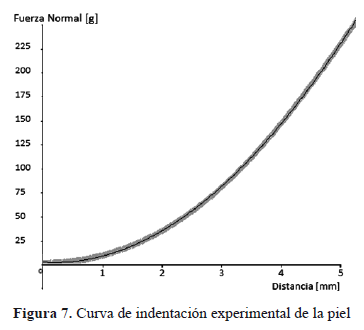
El análisis inverso de los elementos finitos puede ser utilizado para describir cualquier tipo de comportamiento mecánico. En la Figura 7 se muestra una curva de indentación sobre la piel del antebrazo humano, este material no debe considerarse como elástico lineal ya que no se evidencia linealidad en la curva mostrada, por lo que puede emplearse el mismo procedimiento descrito en el artículo para determinar el comportamiento mecánico empleando una ecuación constitutiva diferente a la de la Ley de Hooke, así mismo el algortimo de Levenberg Marquardt debe comparar y proponer valores de módulo equivalente que relacione los coeficientes de la ecuación constitutiva, en lugar de un único módulo como para el caso de los modelos elásticos lineales.
5. CONCLUSIONS
El análisis inverso del comportamiento mecánico mediante el método de los elementos finitos presenta resultados adecuados, por lo que puede ser replicado en otros materiales que presenten comportamiento elástico lineal.
Para este tipo de material, la velocidad de indentación no representa un factor significativo en la respuesta mecánica, de lo que se concluye que puede tener un comportamiento lineal coherente con su capacidad de reversibilidad de las deformaciones.
El método analítico se validó mediante el diseño de experimentos, ya que teóricamente el tipo de indentador no debe incidir en la respuesta mecánica, concluyendo que las ecuaciones empleadas satisfacen el modelo y la obtención del módulo de Young.
REFERENCIAS
[1] Jean-Marc Schwartz, Marc Denninger, Denis Rancourt, Christian Moisan, Denis Laurendeau., Modelling liver tissue properties using a non-linear visco-elastic model for surgery simulation. Medical Image Analysis 9 pp. 103-112, 2005. [ Links ]
[2] Carter, F.J., Frank, T.G., Davies, P.J., Mclean, D. and Cuschieri, A., Measurements and Modeling of the Compliance of Human and Porcine Organs. Med. Image Anal. 5, pp.231-236., 2001. [ Links ]
[3] Forbes, P.A.,Cronin, D.S., Deng, Y.C., Multi-scale human body model to predict side impact thoracic trauma. International Journal of Crash worthiness 11 (3),pp. 203-216, 2006. [ Links ]
[4] Raúl Goncalves, Introducción al Análisis de Esfuerzos. Caracas, Venezuela: 2002. [ Links ]
[5] Truesdell, c., Noll, w., y Antman, s. S., The non-linear field theories of mechanics. Springer, 2004. [ Links ]
[6] Ogden, R.W., Non-Linear Elastic Deformations, ISBN 0-486-69648-0, Dover. 1984. [ Links ]
[7] Saltzman, W., Mark. BIOMEDICAL ENGINEERING - Bridging Medicine and Technology. United States of America : Cambridge University Press, 2009. [ Links ]
[8] Meyers and Chawla Mechanical Behavior of Materials, pp. 98-103, 1999. [ Links ]
[9] Clifford Truesdell & Walter Noll; Stuart S. Antman, The Non-linear Field Theories of Mechanics. Springer. p. 4. ISBN 3540027793. 2004. [ Links ]
[10] Abbas Samani, Donald Plewes., A method to measure the hyperelastic parameters of ex vivo breast tissue samples. 4395, UK : Phys. Med. Biol., Physics in Medicine and Biology, Vol. 49, p. 49, 2004. [ Links ]
[11] Joseph J O'Hagan, and Abbas S. Measurement of the hyperelastic properties of tissue slices with tumour inclusion., Physics in Medicine and Biology, p. 53., 2008. [ Links ]
[12] Plewes, D., Bishop, J., Samani, A., Sciarretta, J., Visualization and quantification of breast cancer biomechanical properties with magnetic resonance elastography. s.l.:Phys. Med. Biol. Vol. 45. , pp.1591-1610, 2000. [ Links ]
[13] Kaster, T., Sack I., Samani, A., Measurement of the hyperelastic properties of ex vivo brain tissue slices. s.l., Journal of Biomechanics, 2011. ISSN: 00219290. [ Links ]
[14] FEROCAST. Ficha técnica. Comercial Feroca, S.A. Madrid. [ Links ]
[15] Montgomery D. Design and Analysis of Experiments, John Wiley & Sons, United States of America, fifth edition, 2001. [ Links ]
[16] Geoffrey A., Tizard, D. O., and Dillard David A., A comparison of experimental methods to determine Poisson's ratio of organic and silicone gel systems to a High degree of precision. Department of Engineering Science and Mechanics [ Links ]
[17] Dowling, N. Mechanical Behavior of Materials. 3rd edition, , Prentice Hall. 2007. [ Links ]
[18] Ramírez J. F., Jaramillo, E. and Vélez, J., A., Algorithm for the prediction of the reactive forces developed in the socket of transfemoral amputees. DYNA. Vol.79, Nro 173, pp. 89-95 Medellin, June 2012. [ Links ]
[19] Wu, J.Z., Herzog, and W., M. Epstein. Evaluation of the finite element software ABAQUS for biomechanical modelling of biphasic tissues. pp. 165-169, s.l.: Journal of Biomechanics, Vol. 31. 1998. [ Links ]
[20] Nicolle, S., Lounis, M., and Willinger, R., Shear properties of brain tissue over a frequency range relevant for automotive impact situations: new experimental results. s.l.: Stapp Car Crash Journal, , Vol. 48., 2004. [ Links ]
[21] Gavin H., The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems. Department of Civil and Environmental Engineering, Duke University. 2011 [ Links ]